星形电阻网络与三角形电阻网络的等效变换
- 格式:ppt
- 大小:161.50 KB
- 文档页数:3
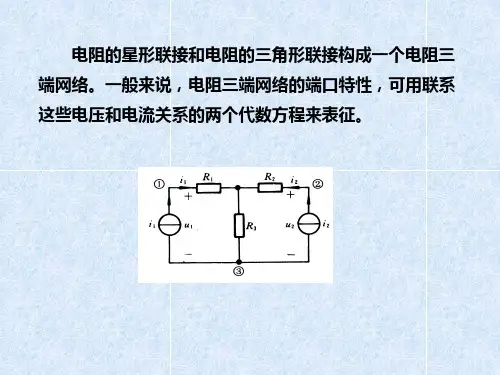



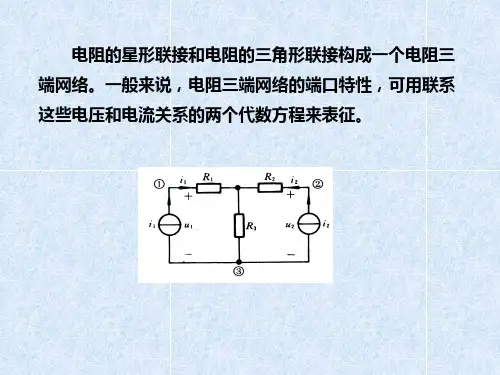
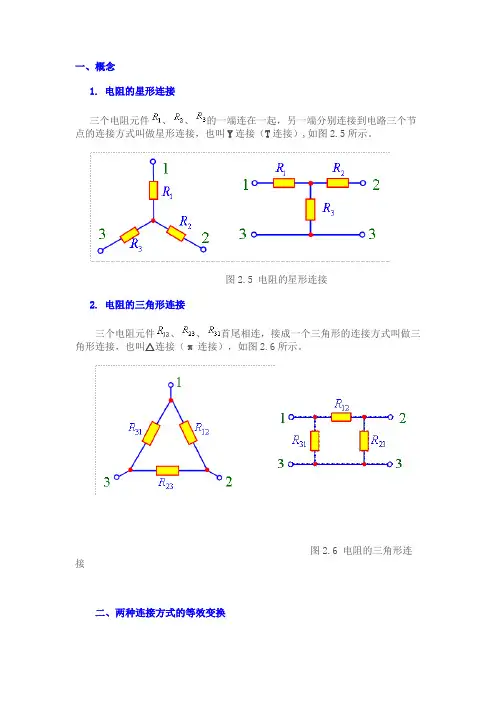
一、概念
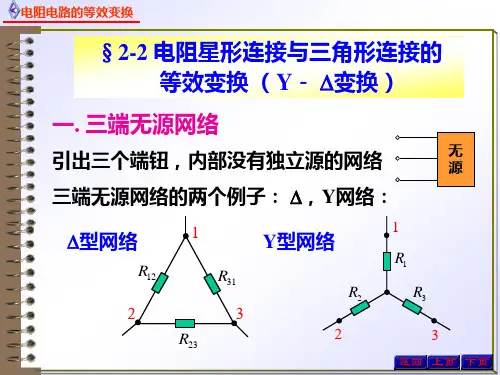
1. 电阻的星形连接
三个电阻元件、、的一端连在一起,另一端分别连接到电路三个节点的连接方式叫做星形连接,也叫Y连接(T连接),如图2.5所示。
图2.5 电阻的星形连接
2. 电阻的三角形连接
三个电阻元件、、首尾相连,接成一个三角形的连接方式叫做三角形连接,也叫△连接(π连接),如图2.6所示。
图2.6 电阻的三角形连接
二、两种连接方式的等效变换
1. 等效变换条件:对应端口的电流、电压均相同
2. 等效变换结果:
①Y →△:
②△→ Y :
三、电阻星形与三角形等效变换步骤:
1. 确定星形或三角形的三个顶点;
2. 去掉在三个顶点内的电阻,换为另一种连接的三个电阻;注意:在三个顶点外的电阻不能动!
3. 计算替换换后的三个电阻阻值;
4. 再按电阻串并联进行等效化简、计算。
例2.5 在图2.7(a)中,求各电阻的电流。
解:将图(a)中顶点acd△连接等效变换为acdY联接,如图2.7(b),则。

星三角电阻转换公式
星三角电阻转换公式是指将三个电阻呈三角形连接的电路转换成呈星型连接的电路时,所需使用的公式。
这个公式可以表示为:RAB = (RA*RB+ RB*RC +RC*RA)/(RC)
其中,RAB是星型电路中A和B之间的等效电阻,RA、RB和RC分别是三角形电路中三个电阻的阻值。
这个公式可以用来计算星型电阻和三角形电阻之间的等效电阻,这样就可以将一种电路拓扑结构转换成另一种,以方便电路设计和分析。
此外,星型电阻和三角形电阻的等效电阻还可以通过其他方法来计算,例如使用矩阵方法或毕奥定理等。
这些方法都可以为工程师和设计师提供准确的电路计算结果。
电阻网络中的三角形星形等效变换在电路中,电阻网络是一个由电阻器连接而成的结构,用于控制电流和电压的传输。
在电阻网络中,基本的电路元件是电阻器,可以通过不同方式进行连接和变换,以达到不同的电流分布和电压分配的目的。
本文将介绍电阻网络中的三角形星形等效变换,以及其在电路设计和分析中的应用。
一、三角形到星形等效变换三角形到星形等效变换指的是将一个由三个电阻器连接而成的三角形电路转化为一个由三个电阻器连接而成的星形电路。
在三角形到星形等效变换中,需要满足以下条件:1. 三个电阻器的连接点形成一个等边三角形;2. 三角形的每个顶点连接一个电阻器;3. 三角形的一个顶点作为星形电路的中心连接点。
通过三角形到星形等效变换,可以改变电路的结构和性质,并简化电路的分析和计算。
二、星形到三角形等效变换星形到三角形等效变换是三角形到星形等效变换的逆过程,即将一个由三个电阻器连接而成的星形电路转化为一个由三个电阻器连接而成的三角形电路。
在星形到三角形等效变换中,需要满足以下条件:1. 三个电阻器连接到一个中心节点,形成一个星形电路;2. 两个相邻的电阻器连接到一个顶点,形成一个等腰三角形;3. 三个电阻器的连接点形成一个等边三角形。
通过星形到三角形等效变换,可以将星形电路转化为三角形电路,使得电路的分析更加简单和方便。
三、等效电阻的计算方法在电阻网络中,等效电阻是指将一个复杂的电路转化为一个简单的电阻网络,使得该电阻网络具有与原电路相同的电流-电压特性。
在三角形星形等效变换中,可以计算出等效电阻。
1. 三角形到星形等效变换中,等效电阻的计算公式为:Rt = R1 * R2 + R2 * R3 + R1 * R3其中,R1、R2、R3分别代表三个电阻器的阻值。
2. 星形到三角形等效变换中,等效电阻的计算公式为:Rt = R1 + R2 + R3其中,R1、R2、R3分别代表三个电阻器的阻值。
通过计算等效电阻,可以将复杂的电阻网络简化为一个等效电阻器,便于电路的计算和分析。
电阻网络中的星形三角形变换分析在电阻网络中,星形和三角形连接是常见的连接方式。
这两种连接方式在电路分析和设计中具有重要的作用。
本文将对电阻网络中的星形三角形变换进行详细分析,以帮助读者更好地理解和应用这一概念。
一、星形连接和三角形连接简介1. 星形连接在电路中,星形连接是指将三个或更多的电阻连接在一起,其中一个节点连接到电源正极,其余节点连接到电源负极。
这种连接方式常用于电路中需要提供共地或共点的情况。
2. 三角形连接三角形连接是指将三个电阻以闭合的三角形连接方式相连。
三角形连接常用于电路中需要提供平衡电路或无共地的情况。
二、星形三角形变换原理星形三角形变换是一种将一个电路转换为与它等效的另一个电路的方法。
通过执行星形三角形变换,可以简化电路的分析和计算。
具体变换原理如下:1. 星型到三角形变换将星形连接的电阻网络转换为等效的三角形连接网络。
设星形连接的电阻为R1,R2,R3,其中节点A连接到电源正极,节点B和C连接到电源负极。
则等效的三角形连接电阻可表示为:RT = R1 * R2 / (R1 + R2 + R3)RA = R1 * R3 / (R1 + R2 + R3)RB = R2 * R3 / (R1 + R2 + R3)2. 三角形到星形变换将三角形连接的电阻网络转换为等效的星形连接网络。
设三角形连接的电阻为RT,RA,RB,其中节点A、B、C两两相连,形成闭合的三角形。
则等效的星形连接电阻可表示为:R1 = RA * RB / (RA + RB + RT)R2 = RA * RT / (RA + RB + RT)R3 = RB * RT / (RA + RB + RT)三、星形三角形变换的应用星形三角形变换在电路分析和设计中具有广泛应用,其中包括但不限于以下几个方面:1. 简化电路分析和计算通过执行星形三角形变换,可以将复杂的电路转换为等效的简化电路,从而简化电路的分析和计算。
这种方法尤其适用于涉及大量电阻和复杂连接的电路。
星形电阻网络与三角形电阻网络的等效变换
(a )为星形(Y 形)电阻网络;(b )为三角形(△形)电阻网络。
1、星形转换为三角形的公式:
记忆口诀为:分母就在对角内,分子两两相乘积。
2
1
3312133221311323211332212332121313322112R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R ++=++=++=++=
++=++=
这三个公式的结构规律可以概括为:三角形网络中一边的电阻,等于星形网 络中联接到两个对应端点的电阻之和再加上这两个电阻之积除以另一电阻。
2、三角形转换为星形的公式:
记忆口诀为:分母三边之和,分子夹边相乘。
31231231
23331
23122312231231231121R R R R R R R R R R R R R R R R R R ++=
++=++=
这三个公式的结构规律可以概括为:星形网络中的一个电阻,等于三角形 网络中联接到对应端点的两邻边电阻之积除以三边电阻之和。
电阻的星型与三角形的等效变换例题在电路中,电阻的星型与三角形的等效变换是解决电路分析问题中常见的一种方法。
通过将星型电阻网络转换为等效的三角形电阻网络,或将三角形电阻网络转换为等效的星型电阻网络,可以简化电路分析过程,使得问题更容易解决。
在本文中,我们将深入探讨电阻的星型与三角形的等效变换,以帮助读者更好地理解这一概念。
1. 电阻的星型与三角形的等效变换概述在电路分析中,星型电阻网络由三个电阻分支组成,形状类似于星型,而三角形电阻网络由三个电阻分支组成,形状类似于三角形。
当需要对这样的电阻网络进行分析时,可以将星型电阻网络转换为等效的三角形电阻网络,或将三角形电阻网络转换为等效的星型电阻网络,从而简化电路分析的复杂度。
2. 电阻的星型与三角形的等效变换原理电阻的星型与三角形的等效变换是基于分析电路中的并联和串联电阻的等效关系。
通过合并相邻的电阻,可以将星型电阻网络转换为等效的三角形电阻网络,或将三角形电阻网络转换为等效的星型电阻网络。
这种等效变换的原理在于保持电路中的等效电阻值不变,从而简化电路分析的过程。
3. 电阻的星型与三角形的等效变换例题分析举例来说,对于一个星型电阻网络,我们可以按照以下步骤将其转换为等效的三角形电阻网络:- 合并星型电阻网络中的相邻电阻,得到等效的三角形电阻网络;- 计算等效的三角形电阻网络的总电阻值。
类似地,对于一个三角形电阻网络,我们可以按照以下步骤将其转换为等效的星型电阻网络:- 合并三角形电阻网络中的相邻电阻,得到等效的星型电阻网络;- 计算等效的星型电阻网络的总电阻值。
通过以上步骤,我们可以将星型与三角形电阻网络之间进行等效变换,从而简化电路分析的过程。
4. 电阻的星型与三角形的等效变换应用举例在实际的电路分析中,电阻的星型与三角形的等效变换可以帮助我们更快速、更精确地分析复杂的电路结构。
以电子电路设计为例,当需要对复杂的电路进行分析与设计时,可以利用星型与三角形的等效变换,将复杂的电路结构简化为更容易分析的形式,从而提高电路设计的效率与精度。
电阻的星形与三角形的等效变换例题电阻的星形与三角形的等效变换是电路分析中常见的问题。
通过等效变换,可以简化复杂的电路结构,使得对电路的分析和计算更加方便和高效。
在本文中,我将针对电阻的星形与三角形的等效变换例题展开讨论,从浅入深地探讨这一主题,帮助您更全面地理解电路分析中的等效变换方法。
1. 电阻的星形与三角形在电路分析中,星形与三角形是两种常见的电阻连接方式。
在星形连接中,三个电阻以一端共同连接在一起,另一端分别连接到电路的其余部分;而在三角形连接中,三个电阻以一端各自连接在一起,另一端也分别连接到电路的其余部分。
针对这种电阻连接方式,我们需要探讨如何进行等效变换,从而简化电路的分析过程。
2. 电阻的星形与三角形的等效变换我们来看一道例题:如何将一个包含星形连接的电阻网络转换为等效的三角形连接?这个问题就涉及到了电路分析中的等效变换方法。
通过分析电路结构和使用等效变换公式,我们可以将星形连接的电阻网络转化为等效的三角形连接,从而简化电路结构,使得后续的计算更加方便和直观。
这个过程需要我们对等效变换公式有深入的理解,以及对电路连接方式的分析能力。
3. 案例分析举一个具体的例子来说明:假设我们有一个包含星形连接的电阻网络,我们需要将其转化为等效的三角形连接。
我们可以根据等效变换的公式,利用电阻的数学关系和连接方式,逐步推导出等效的三角形连接电阻值。
在这个过程中,我们需要考虑电阻之间的串并联关系,以及星形与三角形连接的特点,从而正确地进行等效变换。
4. 总结与回顾通过本文的讨论,我们深入探讨了电阻的星形与三角形的等效变换例题,以及在电路分析中的重要意义。
我们从简到繁地分析了等效变换的原理和方法,帮助您更全面地理解了这一主题。
在深入讨论等效变换的过程中,我们强调了公式推导、案例分析和结论总结的重要性,以及对电路连接方式的理解和分析能力。
5. 个人观点和理解在我看来,电阻的星形与三角形的等效变换是电路分析中的重要内容,它帮助我们简化复杂的电路结构,提高分析和计算的效率。