电阻星形与三角形连接等效变换

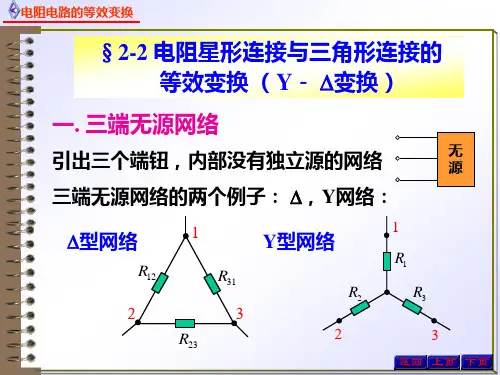
三角形和星形电阻电路的等效变换三角形和星形电阻电路的等效变换，这个话题听起来好像有点高深莫测，但其实它就像是我们日常生活中的一道数学题目。

今天，我就来给大家讲讲这道题目的答案，希望能够帮助大家更好地理解这个概念。

我们来看看三角形电阻电路。

三角形电阻电路是指由三个电阻器组成的电路，这三个电阻器的阻值可以不同。

当我们把这三个电阻器连接在一起时，就会形成一个三角形。

那么，这个三角形电阻电路有什么特点呢？三角形电阻电路的特点就是它的电流分布是均匀的。

这是因为在三角形中，每个顶点都是一个交点，而根据欧姆定律，电流通过交点时会受到阻碍。

所以，当三个电阻器的阻值不它们所承受的电流也会不同。

但是，由于三角形的结构特点，这些电流会被平均分配到每个顶点上，从而使得整个电路的电流分布变得均匀起来。

接下来，我们再来看看星形电阻电路。

星形电阻电路是指由一个电阻器和一个电源组成的电路，这个电阻器的阻值很小，可以忽略不计。

那么，这个星形电阻电路有什么特点呢？星形电阻电路的特点就是它的电流只从正极流向负极。

这是因为在星形结构中，电源的一端连接着一个很小的电阻器，而另一端则直接连接到了负载上。

由于这个小电阻器的阻值很小，所以它对整个电路的影响可以忽略不计。

因此，在星形结构中，电流只会沿着一个方向流动，即从正极流向负极。

那么，如何将这两个电路进行等效变换呢？其实很简单，只需要把三角形电阻电路中的三个电阻器分别替换成一个星形电阻器和两个相同的较小电阻器就可以了。

这样一来，原来的三角形电阻电路就变成了一个由一个星形电阻器和两个相同的较小电阻器组成的新的电路。

这个新的电路的特点是什么呢？这个新的电路的特点就是它的电流分布仍然是均匀的。

这是因为在这个新的电路中，虽然只有一个星形电阻器和两个相同的较小电阻器组成了负载部分，但是由于这两个较小的电阻器的阻值相同且很小，所以它们对整个负载的影响也可以忽略不计。

因此，在整个负载部分中仍然存在着类似于三角形电阻电路中的均匀电流分布情况。

电阻网络中的星形三角形变换分析在电阻网络中，星形和三角形连接是常见的连接方式。

这两种连接方式在电路分析和设计中具有重要的作用。

本文将对电阻网络中的星形三角形变换进行详细分析，以帮助读者更好地理解和应用这一概念。

一、星形连接和三角形连接简介1. 星形连接在电路中，星形连接是指将三个或更多的电阻连接在一起，其中一个节点连接到电源正极，其余节点连接到电源负极。

这种连接方式常用于电路中需要提供共地或共点的情况。

2. 三角形连接三角形连接是指将三个电阻以闭合的三角形连接方式相连。

三角形连接常用于电路中需要提供平衡电路或无共地的情况。

二、星形三角形变换原理星形三角形变换是一种将一个电路转换为与它等效的另一个电路的方法。

通过执行星形三角形变换，可以简化电路的分析和计算。

具体变换原理如下：1. 星型到三角形变换将星形连接的电阻网络转换为等效的三角形连接网络。

设星形连接的电阻为R1，R2，R3，其中节点A连接到电源正极，节点B和C连接到电源负极。

则等效的三角形连接电阻可表示为：RT = R1 * R2 / (R1 + R2 + R3)RA = R1 * R3 / (R1 + R2 + R3)RB = R2 * R3 / (R1 + R2 + R3)2. 三角形到星形变换将三角形连接的电阻网络转换为等效的星形连接网络。

设三角形连接的电阻为RT，RA，RB，其中节点A、B、C两两相连，形成闭合的三角形。

则等效的星形连接电阻可表示为：R1 = RA * RB / (RA + RB + RT)R2 = RA * RT / (RA + RB + RT)R3 = RB * RT / (RA + RB + RT)三、星形三角形变换的应用星形三角形变换在电路分析和设计中具有广泛应用，其中包括但不限于以下几个方面：1. 简化电路分析和计算通过执行星形三角形变换，可以将复杂的电路转换为等效的简化电路，从而简化电路的分析和计算。

这种方法尤其适用于涉及大量电阻和复杂连接的电路。

电阻的星型与三角形的等效变换例题在电路中，电阻的星型与三角形的等效变换是解决电路分析问题中常见的一种方法。

通过将星型电阻网络转换为等效的三角形电阻网络，或将三角形电阻网络转换为等效的星型电阻网络，可以简化电路分析过程，使得问题更容易解决。

在本文中，我们将深入探讨电阻的星型与三角形的等效变换，以帮助读者更好地理解这一概念。

1. 电阻的星型与三角形的等效变换概述在电路分析中，星型电阻网络由三个电阻分支组成，形状类似于星型，而三角形电阻网络由三个电阻分支组成，形状类似于三角形。

当需要对这样的电阻网络进行分析时，可以将星型电阻网络转换为等效的三角形电阻网络，或将三角形电阻网络转换为等效的星型电阻网络，从而简化电路分析的复杂度。

2. 电阻的星型与三角形的等效变换原理电阻的星型与三角形的等效变换是基于分析电路中的并联和串联电阻的等效关系。

通过合并相邻的电阻，可以将星型电阻网络转换为等效的三角形电阻网络，或将三角形电阻网络转换为等效的星型电阻网络。

这种等效变换的原理在于保持电路中的等效电阻值不变，从而简化电路分析的过程。

3. 电阻的星型与三角形的等效变换例题分析举例来说，对于一个星型电阻网络，我们可以按照以下步骤将其转换为等效的三角形电阻网络：- 合并星型电阻网络中的相邻电阻，得到等效的三角形电阻网络；- 计算等效的三角形电阻网络的总电阻值。

类似地，对于一个三角形电阻网络，我们可以按照以下步骤将其转换为等效的星型电阻网络：- 合并三角形电阻网络中的相邻电阻，得到等效的星型电阻网络；- 计算等效的星型电阻网络的总电阻值。

通过以上步骤，我们可以将星型与三角形电阻网络之间进行等效变换，从而简化电路分析的过程。

4. 电阻的星型与三角形的等效变换应用举例在实际的电路分析中，电阻的星型与三角形的等效变换可以帮助我们更快速、更精确地分析复杂的电路结构。

以电子电路设计为例，当需要对复杂的电路进行分析与设计时，可以利用星型与三角形的等效变换，将复杂的电路结构简化为更容易分析的形式，从而提高电路设计的效率与精度。

电阻的星形与三角形的等效变换例题电阻的星形与三角形的等效变换是电路分析中常见的问题。

通过等效变换，可以简化复杂的电路结构，使得对电路的分析和计算更加方便和高效。

在本文中，我将针对电阻的星形与三角形的等效变换例题展开讨论，从浅入深地探讨这一主题，帮助您更全面地理解电路分析中的等效变换方法。

1. 电阻的星形与三角形在电路分析中，星形与三角形是两种常见的电阻连接方式。

在星形连接中，三个电阻以一端共同连接在一起，另一端分别连接到电路的其余部分；而在三角形连接中，三个电阻以一端各自连接在一起，另一端也分别连接到电路的其余部分。

针对这种电阻连接方式，我们需要探讨如何进行等效变换，从而简化电路的分析过程。

2. 电阻的星形与三角形的等效变换我们来看一道例题：如何将一个包含星形连接的电阻网络转换为等效的三角形连接？这个问题就涉及到了电路分析中的等效变换方法。

通过分析电路结构和使用等效变换公式，我们可以将星形连接的电阻网络转化为等效的三角形连接，从而简化电路结构，使得后续的计算更加方便和直观。

这个过程需要我们对等效变换公式有深入的理解，以及对电路连接方式的分析能力。

3. 案例分析举一个具体的例子来说明：假设我们有一个包含星形连接的电阻网络，我们需要将其转化为等效的三角形连接。

我们可以根据等效变换的公式，利用电阻的数学关系和连接方式，逐步推导出等效的三角形连接电阻值。

在这个过程中，我们需要考虑电阻之间的串并联关系，以及星形与三角形连接的特点，从而正确地进行等效变换。

4. 总结与回顾通过本文的讨论，我们深入探讨了电阻的星形与三角形的等效变换例题，以及在电路分析中的重要意义。

我们从简到繁地分析了等效变换的原理和方法，帮助您更全面地理解了这一主题。

在深入讨论等效变换的过程中，我们强调了公式推导、案例分析和结论总结的重要性，以及对电路连接方式的理解和分析能力。

5. 个人观点和理解在我看来，电阻的星形与三角形的等效变换是电路分析中的重要内容，它帮助我们简化复杂的电路结构，提高分析和计算的效率。

电阻的星形与三角形的等效变换
电阻的星形与三角形的等效变换是指将电阻的星型连接电路转化为等效的三角形连接电路，或将三角形连接电路转化为等效的星型连接电路。

具体变换方法如下：
1. 电阻星型转换为等效的电阻三角形：
- 当星型电路中的三个电阻分别为R1、R2、R3时，先计算等效电阻Re：
Re = R1+R2+R3
- 然后计算等效三角形电路中的三个电阻Ra、Rb、Rc：
Ra = [(R2*R3)/(R1+R2+R3)]
Rb = [(R1*R3)/(R1+R2+R3)]
Rc = [(R1*R2)/(R1+R2+R3)]
- 得到等效的电阻三角形连接电路。

2. 电阻三角形转换为等效的电阻星型：
- 当三角形电路中的三个电阻分别为Ra、Rb、Rc时，先计算等效电阻Re：
Re = [Ra*Rb + Rb*Rc + Rc*Ra] / (Ra+Rb+Rc)
- 然后计算等效星型电路中的三个电阻R1、R2、R3：
R1 = [(Ra*Rb*Rc) / (Ra*Rb + Rb*Rc + Rc*Ra)]
R2 = [(Ra*Rb*Rc) / (Ra*Rb + Rb*Rc + Rc*Ra)]
R3 = [(Ra*Rb*Rc) / (Ra*Rb + Rb*Rc + Rc*Ra)]
- 得到等效的电阻星型连接电路。

通过等效变换，可以简化电路分析和计算，从而更方便地求解电路中的电流、电压等参数。

电阻三角形和星形变换公式
电阻三角形和星形变换公式是在电路中常用的一种计算方法，特别是在进行串联和并联电路计算时，可以大大简化计算的复杂度。

电阻三角形和星形变换公式是根据电路的基本原理推导出来的，通过将电路进行转换可以得到等效的电路形式，从而简化计算。

电阻三角形变换公式是指将三个电阻串联的电路转换为三个电阻并联的等效电路的方法。

具体的转换方法是：将三个电阻分别连接成一个三角形，然后将三角形中的任意一个角连接到电路的两端，从而形成一个并联电路。

这样得到的等效电路中，三个电阻的并联等效电阻就是原始电路中三个电阻的串联等效电阻。

星形变换公式是指将三个电阻并联的电路转换为三个电阻串联的等效电路的方法。

具体的转换方法是：将三个电阻分别连接成一个星形，然后将星形的中心点连接到电路的两端，从而形成一个串联电路。

这样得到的等效电路中，三个电阻的串联等效电阻就是原始电路中三个电阻的并联等效电阻。

这两种变换公式在电路的设计和分析中都有着广泛的应用，可以帮助工程师们更加高效地进行电路设计和计算。

在实际应用中，需要根据电路特点选择合适的变换公式，从而得到更加准确和简化的计算结果。

- 1 -。