当前位置：文档之家 › 平面极坐标平面极坐标系和直角坐标系的关系

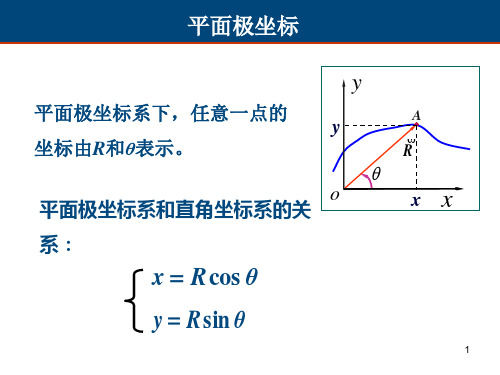
平面极坐标平面极坐标系和直角坐标系的关系

  • 格式：ppt
  • 大小：1.60 MB
  • 文档页数：21

下载文档原格式

  / 21

合集下载

极坐标和直角坐标的转换公式

极坐标和直角坐标的转换公式

极坐标和直角坐标的转换公式在数学中，我们常用直角坐标系和极坐标系来表示平面上的点坐标。

直角坐标系由两条相互垂直的坐标轴组成，分别为水平的 x 轴和垂直的 y 轴。

而极坐标系由一个原点和一个极径组成，极径表示点到原点的距离，极角表示点在极坐标系中与极径的夹角。

在实际问题中，我们常常需要在直角坐标系和极坐标系之间进行转换。

本文将介绍极坐标和直角坐标之间的转换公式。

极坐标转直角坐标首先，假设我们有一个极坐标点，其极径为 r，极角为θ。

要将该点转换为直角坐标系中的点坐标 (x, y)。

那么，我们可以通过以下公式进行计算：x = r * cos(θ)y = r * sin(θ)这里，cos(θ) 表示θ 的余弦值，sin(θ) 表示θ 的正弦值。

例如，我们有一个极坐标点(3, π/4)，要将其转换为直角坐标系中的点坐标。

将 r = 3，θ = π/4 代入上面的公式，我们可以得到：x = 3 * cos(π/4) ≈ 2.121y = 3 * sin(π/4) ≈ 2.121因此，该极坐标点在直角坐标系中的点坐标为 (2.121, 2.121)。

直角坐标转极坐标现在，我们考虑将直角坐标系中的点坐标 (x, y) 转换为极坐标系中的点坐标。

这里，我们假设点 (x, y) 不位于原点。

要将直角坐标转换为极坐标，我们可以使用以下公式：r = sqrt(x^2 + y^2)θ = arctan(y/x)其中，sqrt(x^2 + y^2) 表示平方根，arctan(y/x) 表示 y/x 的反正切值。

举个例子，假设我们有一个直角坐标点 (4, 4)，要将其转换为极坐标系中的点坐标。

将 x = 4，y = 4 代入上面的公式，我们可以得到：r = sqrt(4^2 + 4^2) = sqrt(32) ≈ 5.657θ = arctan(4/4) = arctan(1) ≈ π/4因此，该直角坐标点在极坐标系中的点坐标为(5.657, π/4)。

弹塑性力学 第07章平面问题的极坐标解答

弹塑性力学 第07章平面问题的极坐标解答

ϕ 改变，即与 ϕ 无关。由此可见，凡是轴
对称问题，总是使自变称的 物理量不能存在。
考擦应力函数 U 与 ϕ 无关的一种特殊情况，即轴对称， 此时极坐标形式的双调和方程变成常微分方程 ⎛ ∂2 1 ∂ 1 ∂ 2 ⎞⎛ ∂ 2U 1 ∂U 1 ∂ 2U ⎞ ⎜ ⎜ ∂ρ 2 + ρ ∂ρ + ρ 2 ∂ϕ 2 ⎟ ⎟⎜ ⎜ ∂ρ 2 + ρ ∂ρ + ρ 2 ∂ϕ 2 ⎟ ⎟=0 ⎝ ⎠⎝ ⎠ ⎛ d2 1 d ⎞⎛ d 2U 1 dU ⎞ ⎜ ⎜ d ρ 2 + ρ dρ ⎟ ⎟⎜ ⎜ dρ 2 + ρ dρ ⎟ ⎟=0 ⎝ ⎠⎝ ⎠
τ ρϕ = τ ϕρ
∂ ⎛ 1 ∂U ⎞ 1 ∂ 2U 1 ∂U ⎜ ⎟ =− + 2 =− ⎜ ∂ρ ⎝ ρ ∂ϕ ⎟ ρ ∂ρ∂ϕ ρ ∂ϕ ⎠
¾极坐标系中边界条件的处理： ①、对于由径向线和环向线所围成的弹性体，其边界面通常 均为坐标面，即ρ 面（ρ 为常数）和 ϕ 面（ϕ 为常数），使 边界的表示变得十分简单，所以边界条件也十分简单。 ②、对于应力边界条件，通常给定径向和切向面力值，可直 接与对应的应力分量建立等式（注意符号规定） 应力边界条件：
¾平面问题极坐标形式的几何方程
ερ =
∂u ρ
∂ρ u ρ 1 ∂uϕ εϕ = + ρ ρ ∂ϕ 1 ∂u ρ ∂uϕ uϕ + − γ ρϕ = ρ ∂ϕ ∂ρ ρ
平 面 应 变 问 题
⎧ 1 ⎪ε ρ = (σ ρ −ν 1σ ϕ ) E1 ⎪ ⎪ 1 ⎨ε ϕ = (σ ϕ −ν 1σ ρ ) E1 ⎪ ⎪ 2(1 +ν 1 ) γ τ ρϕ = ⎪ ρϕ E1 ⎩
¾平面问题极坐标形式的物理方程 平 面 应 力 问 题

(完整版)平面极坐标系知识点归纳总结

(完整版)平面极坐标系知识点归纳总结

(完整版)平面极坐标系知识点归纳总结
1. 极坐标系的定义和表示方法
- 极坐标系是一种表示平面上点位置的方法，它由极径和极角两个参数表示。

- 极径表示点到原点的距离，用正数表示。

- 极角表示点到正半轴的角度，用角度或弧度表示。

2. 极坐标系和直角坐标系的转换关系
- 极坐标系和直角坐标系之间可以进行相互转换。

- 直角坐标系中，坐标点的表示方法是 (x, y)，对应的极坐标系中，可以用以下公式转换：
- x = r * cos(θ)
- y = r * sin(θ)
- 其中，r 表示极径，θ表示极角。

3. 极坐标系中的常用图形方程
- 极坐标系中的常用图形方程包括：直线、圆、花瓣线、心形线等。

- 直线的极坐标方程为：θ = α，α 为常数。

- 圆的极坐标方程为：r = a，a 为半径。

- 花瓣线的极坐标方程为：r = a * cos(kθ)，a、k 为常数。

- 心形线的极坐标方程为：r = a * (1 + cos(θ))，a 为常数。

4. 极坐标系中的曲线积分
- 在极坐标系中，曲线积分的计算可以使用以下公式：
- ∮(Pdx + Qdy) = ∫(Pcosθ + Qsinθ) dr
5. 极坐标系的应用领域
- 极坐标系在许多领域中都有应用，例如天文学、电工学、物理学和工程学等。

- 在天文学中，极坐标系用于描述星体的位置和运动。

- 在电工学中，极坐标系用于描述电场和磁场的分布。

以上是平面极坐标系的一些基本知识点归纳总结，希望对你有帮助！。

直角坐标和极坐标的变换关系是什么

直角坐标和极坐标的变换关系是什么

直角坐标和极坐标的变换关系是什么直角坐标系和极坐标系是数学中常见的两种坐标系表示方法，它们之间存在一种特殊的变换关系。

这个关系可以让我们在两种不同的坐标系下进行坐标的转换和计算，从而方便地描述平面上的点位置和运动。

直角坐标系直角坐标系，也称为笛卡尔坐标系，是由两条互相垂直的轴构成的平面坐标系统。

一般来说，我们将水平轴表示为X轴，垂直轴表示为Y轴。

直角坐标系中的点，用一个有序数对 (x, y) 来表示，其中 x 表示点在X轴上的水平位置，y 表示点在Y轴上的垂直位置。

在直角坐标系中，我们可以通过直线的斜率来描述线的特性，以及用向量来表示位移、速度和加速度等概念。

此外，直角坐标系还适用于描述几何图形的方程，如线段、圆、椭圆等。

极坐标系极坐标系是另一种常见的坐标系，它将点的位置表示为极径和极角。

极径表示点到原点的距离，而极角表示该点与极径所在直线的夹角。

在极坐标系中，我们用一个有序数对(r, θ) 来表示点的位置。

其中 r 表示点到原点的距离，θ 表示点与极径所在直线的夹角。

极径通常是非负数，而极角一般采用弧度制表示。

极坐标系的优势在于它对于描述旋转对称的问题特别有用。

例如，绘制圆形、螺旋线等图形时，使用极坐标系比直角坐标系更为方便。

直角坐标系到极坐标系的变换直角坐标系与极坐标系之间存在一种特殊的变换关系。

这个关系允许我们在两种坐标系之间进行转换，从而方便地进行问题的求解。

将直角坐标系中的点(x, y)转换为极坐标系中的点(r, θ)的过程如下：1.计算点(x, y)到原点的距离 r，可以使用勾股定理，即r = √(x^2 +y^2)。

2.计算点(x, y)的极角θ，可以使用反三角函数，即θ = arctan(y / x)。

需要注意的是，当 x 小于0时，需要加上π或180°来调整极角的范围。

将极坐标系中的点(r, θ)转换为直角坐标系中的点(x, y)的过程如下：1.计算点(r, θ)在X轴上的水平位置 x，通过x = r * cos(θ) 得到。

圆周运动加速度切向加速度方向沿切线方向

圆周运动加速度切向加速度方向沿切线方向

0 t 1 2 θ θ 0 0 t t 2 2 2 0 2 ( 0 )
14
用加速度 a an at 判定质点的运动
(1) an 0， at 0 变速率曲线运动： v 方向改变，大小改变。
v 方向改变，大小不变。 (2) an 0， at 0 匀速率曲线运动：
平面极坐标
y
平面极坐标系下，任意一点的
坐标由R和θ表示。 平面极坐标系和直角坐标系的 关系： y
o
A
R

x
x
x R cos θ
y R sin θ
1
自然坐标
在已知质点的运动
轨迹方程时可以选用自 然坐标系。
P1 e t1 · e n1
O1
e n2
O2
P ·
2
et2
自然坐标系下，因为质点的轨迹方程已知，
18
vA
dv at dt
0
t
o
a
2 B
vB

讨论
a a a 109 m s
2 t 2 n
2
A
vA
B
at o arctan 12.4 an
r a n

o
a
17
讨论 解（1）v A 1940 km h
1
A
vA
B

vB 2192 km h r a 3 t 3 s，r 3.5 10 m n
1
at

vB
v vB v A at 而B点 an r t 2 2 at 23.3 m s ，an 106 m s 解得：

平面直角坐标系和极坐标

平面直角坐标系和极坐标

第二节平面直角坐标系和极坐标为了需要，复习一下平面坐标系（直角坐标系和极坐标）一平面直角坐标系1．平面直角坐标系的建立为了确定平面上点的位置：（1）在平面上选定两条互相垂直的直线，并指定正方向（用箭头表示）；（2）以两直线的交点O作为原点；（3）选取任意长的线段作为两直线的公共单位长度；这样，我们就说在平面上建立了一个直角坐标系（图1-2-1）图1-2-1这两条互相垂直的直线叫做坐标轴，习惯上把其中的一条放在水平的位置上，从左到右的方向是正方向，这条轴叫做横坐标轴，简称为横轴或x轴，与x轴垂直的一条叫做纵坐标轴，简称为纵轴或y轴，从下到上的方向是它的正方向。

2. 平面上点的坐标建立了直角坐标系后，平面上的任意一点P的位置就可以确定了，方法是这样的：由P点分别作y轴和x轴的平行线，交点分别是M和N,设x轴上的有向线段OM的数量是a，y轴上有向线段ON的数量是b，我们称a是P点的横坐标，b是P点的纵坐标，写成形式（a，b），这样的一对有序实数（a，b）叫做P点的坐标。

反过来，易知任意一对实数（a，b），都可以确定平面上的一个点.由上面的分析，可以得到下面的结论：在给定的直角坐标系下，对于平面上的任意一点P，我们可以得到唯一的有序实数对（a，b）来和它对应；反过来，对于任何有序实数对，在平面上就能确定唯一的点，这个点的坐标是（a，b）。

就是说，平面上的点和有序实数对（a，b）之间建立了一一对应得关系。

我们在代数里已经知道坐标轴把平面分成了四个部分，每一部分是一个象限。

根据数轴上有向线段的数量，可以理解第I 象限内的点的坐标的符号是（+，+），第II 象限内的是（—，+），第III 象限内的是（—，—），第IV 象限内的是（+，—）。

坐标轴上的点不属于任何象限，在x 轴的正方向上的点，坐标的符号是（+，0）；负方向上的点的坐标符号是（—，0）。

同理， 在y 轴的正方向上的点，坐标的符号是（0，+）；负方向上的点的坐标符号是（0，—）。

1.2.2极坐标和直角坐标的互化

正半轴重合; 3. 两种坐标系的单位长度相同.
例1.
2 将点M的极坐标 (5, ) 3
化成直角坐标.
2 5 解: x 5 cos 3 2 2 5 3 y 5 sin 3 2 5 5 3 ) 所以, 点M的直角坐标为( , 2 2
已知下列点的极坐标，求它们的直 角坐标。
17 ) 6
D. (3,
5 － 6
)
2.在极坐标系中,与(ρ,θ)关于极轴对称 的点是( ) B A.(ρ,θ) B.(ρ, － θ) C.(ρ,θ＋π) D.(ρ,π－θ)
3.在极坐标系中,与点(8, )关于极 6
点对称的点 的一个坐标是( A )
A.(－ 8, 6 )
5 B. (－ 8, － ) 6
练习: 已知点的直角坐标, 求它们 的极坐标.
A ( 3, 3 )
B (1, 3 )
C (5,0) E ( 3,3)
D (0,2)
F (3,0)
题组三 1. 在极坐标系中，与点 (3, )重合 6 的点是( A ) 13 A.(3, 6 ) B. (3, － 6 )
C. (3,
5 C. (－8, 6 )
D.(－8, － ) 6
A ( 3, ) 6

B ( 2, ) 2

C (1, ) 2

3 3 D ( , ) E ( 2, ) 2 4 4
3 F (0, ) 4
例2. 将点M的直角坐标
( 3, 1)
化成极坐标.
（ 1 ）2 解: ( 3 )
2 2
1 3 tan 3 3 7 因为点在第三象限, 所以 6 7 因此, 点M的极坐标为( 2, ) 6

2-7极坐标系


& & v = ρe ρ + ρϕeϕ && && & && a = ( ρ − ρϕ )e ρ + ( ρϕ + 2 ρϕ )eϕ
2
径向速度 横向速度
dθ v v e 通常圆周运动时径向速度为0，这时： 通常圆周运动时径向速度为 ，这时： v(t) = r θ dt
这时常引入角速度矢量 定义： 定义：
ω
r
dθ 大 ：ω = 小 v = rω dt v v v 方 ：ω er e 满足右手定则 向 、 、θ
ω
v
质点的加速度为： 质点的加速度为： v v er e o v θ dθ v v dv d dr v a = = ( er +r e ) θ dt dt dt dt d2r dθ 2 v d2θ dr dθ v v v = 2 −r( ) er +r 2 +2 θ θ e = arer +aθ e dt dt dt dt dt 径向加速度 讨论： 讨论： 横向加速度
ρ
O
ϕ
A x
r (t ) = ρ e ρ
二、径向速度与横向速度
平面极坐标的径向单位矢量和横向单位矢量是随时间变化 是时间的函数，如果将它们用直角坐标来表示， 的，是时间的函数，如果将它们用直角坐标来表示，
e ρ = cos ϕ i + sin ϕ j e ϕ = − sin ϕ i + cos ϕ j
这两个单位矢量随时间的变化为： 这两个单位矢量随时间的变化为：
de ρ dt deϕ dt
& & = ( − sin ϕ i + cos ϕ j )ϕ = ϕ e ϕ & & = ( − cos ϕ i - sin ϕ j )ϕ = − ϕ e ρ

极坐标系与平面极坐标系

极坐标系与平面极坐标系在数学中，极坐标系是一种用极径和极角来描述平面上点的坐标系。

它与我们常见的直角坐标系有着不同的表示方式和应用场景。

本文将介绍极坐标系以及它在数学和物理学中的应用。

一、极坐标系的定义与表示方法极坐标系由两个参数构成，即极径和极角。

极径表示点到原点的距离，极角表示点与极轴的夹角。

在极坐标系中，我们可以通过极径和极角来唯一地确定一个点的位置。

在平面直角坐标系中，我们用(x,y)来表示一个点的坐标，其中x表示点在x轴上的投影，y表示点在y轴上的投影。

而在极坐标系中，我们用(r,θ)来表示一个点的坐标，其中r表示点到原点的距离，θ表示点与极轴的夹角。

二、极坐标系的转换与应用极坐标系与直角坐标系之间可以相互转换。

对于给定的直角坐标系中的点(x,y)，我们可以通过以下公式将其转换为极坐标系中的点(r,θ)：r = √(x^2 + y^2)θ = arctan(y/x)同样地，对于给定的极坐标系中的点(r,θ)，我们可以通过以下公式将其转换为直角坐标系中的点(x,y)：x = r * cos(θ)y = r * sin(θ)极坐标系在数学和物理学中有着广泛的应用。

在数学中，它常用于描述极限、曲线的方程和曲线积分等问题。

在物理学中，极坐标系常用于描述圆形运动、天体运动和电磁场等问题。

三、平面极坐标系的特点与优势平面极坐标系相比于直角坐标系具有一些独特的特点和优势。

首先，平面极坐标系能够更直观地描述圆形和极坐标对称的问题。

对于圆形运动或者具有极坐标对称性的问题，使用极坐标系可以简化计算和分析过程。

其次，平面极坐标系能够更好地描述极限和无穷远点。

在直角坐标系中，当一个点趋于无穷远时，其坐标值会趋于无穷大。

而在极坐标系中，当一个点趋于无穷远时，其极径会趋于无穷大，而极角则可以保持不变。

最后，平面极坐标系在描述圆形区域和环形区域时更加简洁明了。

在直角坐标系中，我们需要使用多个方程来描述一个圆形或环形区域。

1.2.2极坐标系与直角坐标的关系

3
化成直角坐标.
解: x 5cos 2 5
32
y 5sin 2 5 3
32 所以, 点M的直角坐标为( 5 , 5 3 )
22
已知下列点的极坐标，求它们的直 角坐标。
A (3, )
B (2, )
C (1, )
6
2
2
D (3, )
24
E (2, 3 )
4
例2. 将点M的直角坐标 ( 3,1)
化成极坐标.
解: ( 3)2 （ 1）2 2
tan 1 3
3 因为点在第三象限,
3 所以
7
6
因此, 点M的极坐标为(2, 7 )
6
练习: 已知点的直角坐标, 求它们 的极坐标.
A (3, 3) C (5,0)
B (1, 3) D (0,2)E (Fra bibliotek,3)小结
极坐标与直角坐标的互化关系式:
极坐标和直角坐标的互化
平面内的一个点的直角坐标是(1, 3 ) 这个点如何用极坐标表示?
把直角坐标系中的 原点作为极点,x轴的正 半轴作为极轴, 并且两 种坐标系中取相同的长 度单位
y
M (1, 3)
θ
O
x
设点M的极坐标为(ρ,θ)
12 （ 3）2 2 tan 3 3
1
极坐标与直角坐标的互化关系式: 一般地，设点M的直角坐标是
(x, y)极坐标是 (ρ,θ)
2 x2 y2 , tan y ( x 0)
x
x=ρcosθ, y=ρsinθ
互化公式的三个前提条件： 1. 极点与直角坐标系的原点重合; 2. 极轴与直角坐标系的x轴的正半
轴重合; 3. 两种坐标系的单位长度相同.
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

an

v2 R
─ 法向加速度或向心加速度 方向指向圆心，其值为正。
an是引起速度方向改变的加速度。
9
圆周运动加速度
圆周运动加速度
a

at

an

Ret

Rω2en
大小 a at2 an2
方向 θ tan 1 an at
不一定再指向圆心
y
a
en vet
o
x
10
19
讨论
a at2 an2 109 m s2
arctan at 12.4o
an
A
r an

o
v A
B
a
at
v B
（2）矢径 r所转过的角度

At

1t 2
2
s

r

v At

1 2
att 2
1722 m
20
SUCCESS
THANK YOU
运动方程为 2 3t 3
式中 以弧度计，t以秒计，求：
(1) t=2s时，质点的切向和法向加速度； (2) 当总加速度的方向和切向加速度成
45o角时，其角位移 是多少?
如果给出的运动方程形式是直角坐标系下 的，该如何求解？
17
讨论
例2 一歼击机在 A
高空 点A时的水平速率为1
v A
B
940 km·h-1 ,沿近似圆弧 r
曲线俯冲到点B，其速率为
2 192 km·h-1 , 经历时 o
v B
间为AB3 s , 设
的半
飞径机约从为A到3.B5过k程m 视, 为匀变速率圆周运动，不计
重力加速度的影响，求：(1) 飞机在点B的加
速度；(2)飞机由点A到点B所经历的路程.
18
讨论

det dt

dθ dt
en

v v et
et 2

et1

O enR
法向单位矢量
法向单位矢量
法向加速度
an vω
ω2R

v2 R

et

et1
et 2
8
圆周运动加速度
at

dv dt
─ 切向加速度 方向沿切线方向，可正可负。
a t是引起速度大小改变的加速度。

t0 t
dv dt
et

v
det dt
dt
切向加速度
at

dv dt

R
d
dt

R

d 2s dt 2
角加速度
v 2

et2 v1
o
et1
R
v2
v1
et 2
et1
7
圆周运动法向加速度
a

dv dt
et

v
det dt
切向单位矢量

· lim Δet · Δt0 Δt
4
圆周运动速率
在平面极坐标系下，
s s(t) R (t)
速率
v lim Δs R lim Δθ
Δt0 Δt
Δt0 Δt
v(t) R(t)
y B
R
e tA

o
x
5
圆周运动速度
速度
v

lim
r

lim
r
lim
s
t0 t
lim r t0 s
s s(t)
2
圆周运动的角量
在平面极坐标系下,r =常量。
角坐标 (t ) 角位移
单位：rad。
角速度
lim d
t0 t dt
单位rad·s-1
y
B
r A

o
x
3
圆周运动的角量
角加速度
lim dω
t0 t dt
单位rad·s-2
t0 s
r
lim
t 0
s
et
t 0
et
t
lim s v R(t)
t0 t
v

vet

ds dt
et


R(t)et
y B
R
e tA

o
x
6
圆周运动切向加速度
作变速率圆周运动时
质点加速度
a lim v d vet
解（1）vA 1940 km h 1 A
v A
vB 2192 km h1
t 3s，r 3.5103 m
vB vA
dv

at
t
dt
0
r an

o
B
a
at
v B
at

vB
vA t
而B点
an

vB2 r
解得：at 23.3m s2，an 106 m s2
SUCCESS
THANK YOU
2019/10/31
圆周运动加速度
【思考】质点能否按图示的加速度沿圆周运动？如 果能，分别表示什么情形？
a1 0 a2 a3
a4 圆周运动加速度总
指向圆内侧
推广：曲线运动加速度 总指向曲线内凹一侧
12
角量和线量的关系
ds Rdθ
v ds R dθ Rω dt dt
dω dt
ω
t
dω dt
ω0
0
如 t 0 时, 0, 0

θ
0 t θ0 0t

1 2
t
2

2

2 0

2 (
0)
15
用加速度 a an at 判定质点的运动
(1) an

0，at

0 变速率曲线运动：v
2019/10/31
方向改变，大小改变。
(2) an

0，at

0 匀速率曲线运动：v 方向改变，大小不变。
(3) an 0，at 0 变速率直线运动：v 方向不变，大小改变。
(4) an 0，at 0 匀速率直线运动：v 方向不变，大小不变。
16
例题
例1： 一质点沿半径为1m的圆周运动，
平面极坐标
平面极坐标系下，任意一点的 坐标由R和θ表示。
平面极坐标系和直角坐标系的
关系：
x Rcos θ
y Rsin θ
y
y
o
A
R
xx
1
自然坐标
在已知质点的 运动轨迹方程时可以选 用O1
· O2
en2
et2
P2
自然坐标系下，因为质点的轨迹方程已 知，所以用弧长来描述质点的运动：
an

v2 R

Rω2
at

dv dt

R
dω dt

Rα
y
B ds
R d A

o
x
13
匀速率圆周运动
特点
v 常量
速度方向改变，大小不变。
at a
R
an
0 anen

Rω2en
0
常量
0 t
14
匀变速率圆周运动
特点 dω 常量
dt