第四章立体的投影讲义
- 格式:ppt
- 大小:961.50 KB
- 文档页数:26







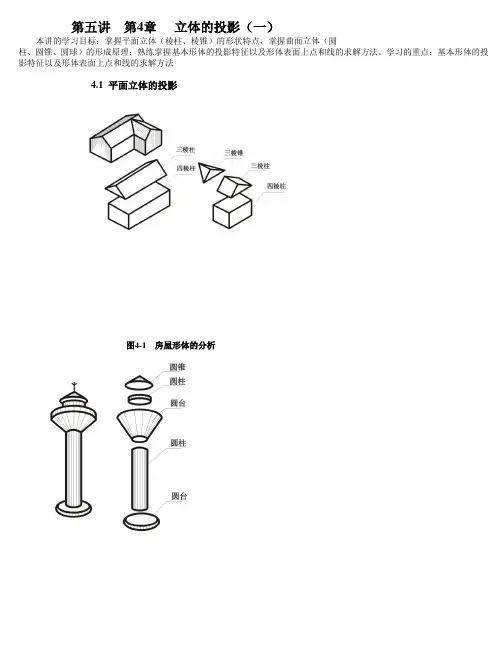
第五讲第4章立体的投影(一)本讲的学习目标:掌握平面立体(棱柱、棱锥)的形状特点,掌握曲面立体(圆柱、圆锥、圆球)的形成原理;熟练掌握基本形体的投影特征以及形体表面上点和线的求解方法。
学习的重点:基本形体的投影特征以及形体表面上点和线的求解方法4.1 平面立体的投影图4-1 房屋形体的分析图4-2 水塔形体的分析基本形体:组成形体的最简单但又规则的几何体,叫做基本形体。
基本形体的分类:根据表面的组成情况,基本形体可分为平面立体和曲面立体两种。
平面立体:表面由若干平面围成的基本体,叫做平面立体。
平面立体类型:有棱柱、棱锥、棱台等。
平面体的投影:作平面立体的投影,就是作出组成平面立体的各平面的投影。
4.1.1 棱柱4.1.1.1 棱柱的投影如图4-3所示,有两个三角形平面互相平行,其余各平面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些平面所围成的基本体称为棱柱。
图4-3 三棱柱体当底面为三角形、四边形、五边形……时,所组成的棱柱分别为三棱柱、四棱柱、五棱柱等。
(a)立体图(b)投影图图4-4 三棱柱的三面投影分析其三面投影图:W投影:投影为三角形。
H投影:投影为两个矩形。
V投影:投影为一个矩形。
4.1.1.2 棱柱表面定点和定线【例4-1】如图4-5所示,已知三棱柱上直线AB、BC的V投影,求另外两个投影。
(a)已知条件(b)作图图4-5 三棱柱表面上的点和线【例4-2】如图4-5所示,已知四棱柱表面上点K的V投影和点M的V投影,求它们的另外两投影。
(a)立体图(b)已知条件(c)作图图4-6 四棱柱表面上的点4.1.2 棱锥定义:由一个多边形平面与多个有公共顶点的三角形平面所围成的几何体称为棱锥。
如图4-6所示为三棱锥。
图4-7-1 三棱锥根据不同形状的底面,棱锥有三棱锥、四棱锥和五棱锥等。
当棱锥底面为正n边形时,称为正n棱锥。
4.1.2.1 棱锥的投影1. 棱锥如图4-7所示为一正三棱锥,三棱锥底面ABC是水平面,后棱面SAC是侧垂面,其它两个侧面都是一般面;棱线SB为侧平线,其它两条棱线为一般线。