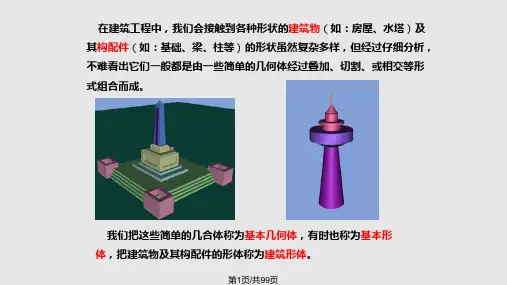
第四章立体的投影空间物体可以看作是由一些简单的几何体所组成。
而这些简单的几何体又是由一些表面围成。
根据这些表面的性质，几何体可分为平面立体和曲面立体两类。
本章主要介绍常见的一些立体的投影表达及它们的三视图画法，为进一步分析复杂的物体打下基础。
概 述常见的基本立体平面立体曲面立体棱柱 棱锥圆柱 圆锥圆球圆环•平面立体侧表面的交线称为棱线。
•若平面立体所有棱线互相平行，称为棱柱。
•若平面立体所有棱线交于一点，称为棱锥。
平面立体：由若干平面所围成的几何体, 如棱柱、棱锥等。
§1 平面立体的投影棱柱棱锥是平面立体各表面投影的集合, 是由直线段组成的封闭图形。
平面立体的投影1.1 棱柱1.1.1 三棱柱的视图三棱柱由两个底面和三个侧棱面组成。
投影称为左视图。
展开后得到三棱柱的三视图如下：三视图之间的投影规律：(1) 度量关系：长对正，高平齐，宽相等。
(2) 位置关系：俯视图—前后、左右；主视图—上下、左右；左视图—上下、前后。
三棱柱的两底面为水平面，在俯视图中反映实形。
其余三个侧棱面都是铅垂面，水平投影积聚，与三角形的边重合。
三棱柱的视图但三视图之间的投影关系，应严格遵守。
点的可见性规定：若点所在平面的投影可见，点的投影可见；若平面的投影积聚成直线，点的投影也可见。
1.1.2 三棱柱表面的点由于三棱柱的表面都是平面，所以在三棱柱的表面上取点与在平面上取点的方法相同。
m m 'k 'kk "m "1.1.2 斜三棱柱视图及其表面的直线分清直线所在表面，然后在平面上求直线投影。
平面立体投影可见性的判别规律：1)在平面立体的每一投影中，其外形轮廓线都是可见的。
2)在平面立体的每一投影中，外形轮廓线内的直线的可见性，相交时可利用交叉两直线的重影点来判别。
3)在平面立体的每一投影中，外形轮廓线内，若多条棱线交于一点，且交点可见，则这些棱线均可见，否则均不可见。
4)在平面立体的每一投影中，外形轮廓线内，两可见表面相交，其交线为可见。
