第3[1].4-3.5-3.6_竞聚率与Q-e方程

竞聚率的概念及影响竞聚率大小的因素竞聚率：共聚反应中自聚能力与共聚能力的比值。

影响竞聚率大小的因素（1）温度竞聚率由两个速率常数k11与k12之比构成, 所以可用Arrhenius方程来讨论温度对其影响。

r1 < 1表示k11 < k12, 即E11 > E12. 温度上升, 活化能较大的增长速率常数k11增长较快, r1逐渐上升, 趋于1。

r1 > 1表示k11 > k12, 即E11 < E12. 温度上升, 活化能较大的增长速率常数k12增长较快, r1下降, 也趋于1。

温度上升, 共聚反应向理想共聚方向发展。

（2）压力竞聚率对压力的变化也不敏感，大体上向理想共聚的方向移动。

（3）溶剂溶剂对自由基共聚的竞聚率一般没有影响. 如果两种单体极性不同, 那么两种单体随溶剂极性改变, 其反应活性变化的趋势也会不同, 也会使r发生改变. 在离子型聚合中, 溶剂将影响聚合离子对的松紧程度, 因此溶剂对聚合速率和竞聚率有较大影响。

（4）其他因素反应介质对单体竞聚率的影响较复杂, 大致体现在以下几方面：a.粘度——不同反应介质可能造成体系粘度不同, 而在不同粘度下, 两种单体的扩散性质可能不同, 从而导致k11和k12的变化不同而改变r 值。

b.pH值——酸性单体或碱性单体的聚合反应速率与体系pH值有关, 如丙烯酸与苯乙烯共聚时, 丙烯酸会以离解型和非离解型两种反应活性不同的形式平衡存在, pH值不同会导致平衡状态的改变, r 值也随之改变. 盐类化合物---若反应介质中存在盐类物质, 将使共聚反应趋向于交替共聚。

c.聚合方法——聚合方法不同而导致竞聚率存在差异实际上是由于反应区域的局部浓度与体系宏观平均浓度不同引起的, 而不是竞聚率本身有什么变化. 乳液聚合或悬浮聚合体系, 如果两种单体的扩散速度或在水中的溶解速度相差较大, 将使得反应微区的局部单体浓度比往往不同于本体或溶液等均相共聚体系, 从而影响共聚物组成。

高分子化学潘仁祖(第五版)第一至第六章习题第一章绪论思考题 1. 举例说明单体、单体单元、结构单元、重复单元、链节等名词的含义，以及它们之间的相互关系和区别。

2. 举例说明低聚物、齐聚物、聚合物、高聚物、高分子、大分子诸名词的的含义，以及它们之间的关系和区别。

3. 写出聚氯乙烯、聚苯乙烯、涤纶、尼龙-66、聚丁二烯和天然橡胶的结构式。

选择其常用分子量，计算聚合度。

4. 举例说明和区别：缩聚、聚加成和逐步聚合，加聚、开环聚合和连锁聚合。

5. 写出下列单体的聚合反应式，以及单体、聚合物的名称。

6. 按分子式写出聚合物和单体名称以及聚合反应式。

属于加聚、缩聚还是开环聚合，连锁聚合还是逐步聚合？7. 写出下列聚合物的单体分子式和常用的聚合反应式：聚丙烯腈、天然橡胶、丁苯橡胶、聚甲醛、聚苯醚、聚四氟乙烯、聚二甲基硅氧烷。

8. 举例说明和区别线形结构和体形结构、热塑性聚合物和热固性聚合物、非晶态聚合物和结晶聚合物。

9. 举例说明橡胶、纤维、塑料的结构-性能特征和主要差别。

10. 什么叫玻璃化温度？橡胶和塑料的玻璃化温度有何区别？聚合物的熔点有什么特征？计算题 1. 求下列混合物的数均分子量、质均分子量和分子量分布指数。

a、组分A：质量= 10g，分子量= 30 000；b、组分B：质量= 5g，分子量= 70 000；c、组分C：质量= 1g，分子量= 100 000 2. 等质量的聚合物A和聚合物B共混，计算共混物的Mn和Mw。

聚合物A：Mn=35,000, Mw =90,000；聚合物B：Mn=15,000, Mw=300,000第2章缩聚与逐步聚合计算题1. 通过碱滴定法和红外光谱法，同时测得g聚己二酰己二胺试样中含有?10-3mol羧基。

根据这一数据，计算得数均分子量为8520。

计算时需作什么假定？如何通过实验来确定的可靠性？如该假定不可靠，怎样实验来测定正确的值？ 2. 羟基酸HO-(CH2)4-COOH进行线形缩聚，测得产物的质均分子量为18,400 g/mol-1，试计算：a. 羧基已经醌化的百分比 b. 数均聚合度 c. 结构单元数Xn 3. 等摩尔己二胺和己二酸进行缩聚，反应程度p为、、、、、、，试求数均聚合度Xn、DP和数均分子量Mn，并作Xn－p关系图。

第4章一元一次方程（压轴必刷30题3种题型专项训练）一．一元一次方程的解（共2小题）1．（2022秋•启东市校级月考）我们规定，若关于x的一元一次方程ax＝b的解为x＝b﹣a，则称该方程为“差解方程”，例如：2x＝4的解为2，且2＝4﹣2，则方程2x＝4是差解方程．请根据上述规定解答下列问题：（1）判断3x＝4.5是否是差解方程；（2）若关于x的一元一次方程5x＝m+1是差解方程，求m的值．2．（2022秋•宿城区期中）我们规定，若关于x的一元一次方程ax＝b的解为b﹣a，则称该方程为“差解方程”，例如：2x＝4的解为2，且2＝4﹣2，则方程2x＝4是差解方程．请根据上边规定解答下列问题：（1）判断3x＝4.5是否是差解方程；（2）若关于x的一元一次方程6x＝m+2是差解方程，求m的值．二．解一元一次方程（共3小题）3．（2021秋•高新区期末）用“*”定义一种新运算：对于任意有理数a和b，规定a*b＝ab2+2ab+a．如：1*3＝1×32+2×1×3+1＝16（1）求2*（﹣2）的值；（2）若（其中x为有理数），试比较m，n的大小；（3）若＝a+4，求a的值．4．（2022秋•工业园区校级月考）如图，小明在一张纸面上画了一条数轴，折叠纸面，使表示数﹣1的点与表示数5的点重合，请你回答以下问题：（1）表示数﹣2的点与表示数的点重合；表示数7的点与表示数的点重合．（2）若数轴上点A在点B的左侧，A，B两点之间的距离为12，且A，B两点按小明的方法折叠后重合，则点A表示的数是；点B表示的数是；（3）已知数轴上的点M分别到（2）中A，B两点的距离之和为2022，求点M表示的数是多少？5．（2021秋•溧阳市期末）阅读理解学：我们都应该知道，任何无限循环小数都应该属于有理数，那是因为所有无限循环小数都可以化成分数形式，而分数属于有理数．那么无限循环小数怎么化成分数呢？下面的学习材料会告诉我们原因和方法：问题：利用一元一次方程将0.化成分数．设0.＝x．由0.＝0.7777…，可知10×0.＝7777…＝7+0.7777…＝7+0.，即10x＝7+x．可解得，即0.＝．（1）将0.直接写成分数形式为．（2）请仿照上述方法把下列小数化成分数，要求写出利用一元一次方程进行解答的过程．①0.；②0.1．三．一元一次方程的应用（共25小题）6．（2022秋•高新区期末）甲、乙两个旅行团同时去苏州旅游，已知乙团人数比甲团人数多4人，两团人数之和恰等于两团人数之差的18倍．（1）问甲、乙两个旅行团的人数各是多少？（2）若乙团中儿童人数恰为甲团中儿童人数的3倍少2人，某景点成人票价为每张100元，儿童票价是成人票价的六折，两旅行团在此景点所花费的门票费用相同，求甲、乙两团儿童人数各是多少？7．（2022秋•兴化市校级期末）甲、乙两班学生到集市上购买苹果，苹果的价格如表：50千克以上购买苹果数不超过30千克30千克以上但不超过50千克每千克价格3元 2.5元2元甲班分两次共购买苹果80千克（第二次多于第一次），共付出185元，乙班则一次购买苹果80千克．（1）乙班比甲班少付出多少元？（2）甲班第一次、第二次分别购买苹果多少千克？8．（2023秋•海门市校级月考）已知A、B、C三点在同一条数轴上，点A、B表示的数分别为﹣2，18，点C在原点右侧，且AC＝AB．（1）A、B两点相距个单位；（2）求点C表示的数；（3）点P、Q是该数轴上的两个动点，点P从点A出发，沿数轴以每秒1个单位的速度向右运动，点Q 从点B出发，沿数轴以每秒2个单位的速度向左运动，它们同时出发，运动时间为t秒，求当t为何值时，P、Q两点到C点的距离相等？9．（2022秋•建邺区校级期末）扬子江药业集团生产的某种药品的长方体包装盒的侧面展开图如图所示．根据图中数据，如果长方体盒子的长比宽多4cm，求这种药品包装盒的体积．10．（2023秋•滨海县月考）生活与数学日一二三四五六12345678910111213141516171819202122232425262728293031（1）山姆同学在某月的日历上圈出2×2个数，如图1，正方形的方框内的四个数的和是48，那么这四个数是．（2）小丽也在上面的日历上圈出2×2个数，如图2，斜框内的四个数的和是46，则它们分别是．（3）刘莉也在日历上圈出5个数，呈十字框形，如图3，它们的和是55，则中间的数是．（4）某月有5个星期日的和是75，则这个月中最后一个星期日是号？11．（2022秋•兴化市校级月考）结合数轴与绝对值的知识回答下列问题：（1）探究：①数轴上表示5和2的两点之间的距离是．②数轴上表示﹣1和﹣5的两点之间的距离是．③数轴上表示﹣3和4的两点之间的距离是．（2）归纳：一般的，数轴上表示数a和数b的两点之间的距离等于．（3）应用：①若数轴上表示数a的点位于﹣4与3之间，则|a+4|+|a﹣3|的值＝．②若a表示数轴上的一个有理数，且|a﹣1|＝|a+3|，则a＝．③若a表示数轴上的一个有理数，|a﹣1|+|a+2|的最小值是．④若a表示数轴上的一个有理数，且|a+3|+|a﹣5|＞8，则有理数a的取值范围是．（4）拓展：已知，如图2，A、B分别为数轴上的两点，A点对应的数为﹣20，B点对应的数为100．若当电子蚂蚁P 从A点出发，以4个单位/秒的速度向右运动，同时另一只电子蚂蚁Q恰好从B点出发，以3单位/秒的速度向左运动，求经过多长时间两只电子蚂蚁在数轴上相距20个单位长度，并写出此时点P所表示的数．12．（2022秋•海安市月考）已知：在一条东西向的双轨铁路上迎面驶来一快一慢两列火车，快车长AB＝2（单位长度），慢车长CD＝4（单位长度），设正在行驶途中的某一时刻，如图，以两车之间的某点O为原点，取向右方向为正方向画数轴，此时快车头A在数轴上表示的数是a，慢车头C在数轴上表示的数是b．若快车AB以6个单位长度/秒的速度向右匀速继续行驶，同时慢车CD以2个单位长度/秒的速度向左匀速继续行驶，且|a+8|+（b﹣16）2＝0．（1）求此时刻快车头A与慢车头C之间相距单位长度；（2）从此时刻开始算起，问再行驶多少秒钟两列火车行驶到车头AC相距8个单位长度？（3）此时在快车AB上有一位爱动脑筋的七年级学生乘客P，他发现行驶中有一段时间t秒钟，他的位置P到两列火车头A、C的距离和加上到两列火车尾B、D的距离和是一个不变的值（即P A+PC+PB+PD 为定值）．你认为学生P发现的这一结论是否正确？若正确，求出这个时间及定值；若不正确，请说明理由．13．（2022秋•淮阴区期中）据电力部门统计，每天8：00至21：00是用电高峰期，简称“峰时”，21：00至次日8：00是用电低谷期，简称“谷时”．为了缓解供电需求紧张的矛盾，我市电力部门拟逐步统一换装“峰谷分时”电表，对用电实行“峰谷分时电价”新政策，具体见下表： 时间换表前换表后峰时（8：00﹣21：00）谷时（21：00﹣8：00）电价每度0.52元每度0.55元每度0.30元小明家对换表后最初使用的95度电进行测算，经测算比换表前使用95度电节约了5.9元，问小明家使用“峰时”电和“谷时”电分别是多少度？14．（2022秋•姜堰区期中）阅读理解：M 、N 、P 为数轴上三点，若点P 到M 的距离是点P 到N 的距离的k （k ＞0）倍，即满足PM ＝k ．PN 时，则称点P 关于M 、N 的“相对关系值”为k ．例如，当点M 、N 、P 表示的数分别为0、2、3时，PM ＝3PN ，则称点P 关于M 、N 的“相对关系值”为3；PN ＝MN ，则称点N 关于P 、M 的“相对关系值”为．如图，点A 、B 、C 、D 在数轴上，它们所表示的数分别为﹣1、2、6、﹣6．（1）原点O 关于A 、B 的“相对关系值“为a ，原点O 关于B 、A 的“相对关系值”为b ，则a ＝ ，b ＝ ．（2）点E 为数轴上一动点，点E 所表示的数为x ，若x 满足|x +3|+|x ﹣2|＝5，且点E 关于C 、D 的“相对关系值”为k ，则k 的取值范围是 ．（3）点F 从点B 出发，以每秒1个单位的速度向左运动，设运动时间为t （t ＞0）秒，当经过t 秒时，C 、D 、F 三点中恰有一个点关于另外两点的“相对关系值”为2，求t 的值．15．（2022秋•苏州期中）【问题背景】落实“双减”政策后，某校开展了丰富多彩的科技活动．如图1，电子蚂蚁P 、Q 在长18分米的赛道AB 上同时相向匀速运动，电子蚂蚁P 从A 出发，速度为4分米/分钟，电子蚂蚁Q从B出发，速度为2分米/分钟，当电子蚂蚁P到达B时，电子蚂蚁P，Q停止运动．经过几分钟P，Q之间相距6分米？【问题解决】小辰同学在学习《有理数》之后，发现运用数形结合的方法建立数轴可以较快地解决上述问题：如图2，将点A与数轴的原点O重合，点B落在正半轴上．设运动的时间为t（0≤t≤4.5）．（1）t分钟后点P在数轴上对应的数是；点Q对应的数是；（用含t的代数式表示）（2）我们知道，如果数轴上M，N两点分别对应数m，n，则MN＝|m﹣n|．试运用该方法求经过几分钟P，Q之间相距6分米？（3）在赛道AB上有一个标记位置C，AC＝6．若电子蚂蚁P与标记位置C之间的距离为a，电子蚂蚁Q与B之间的距离为b．在运动过程中，是否存在某一时刻t，使得a+b＝4？若存在，请求出运动的时间；若不存在，请说明理由．16．（2022秋•海陵区校级月考）阅读理解，完成下列各题：定义：已知A、B、C为数轴上任意三点，若点C到点A的距离是它到点B的距离的3倍，则称点C是[A，B]的3倍点，例如：如图1，点C是[A，B]的3倍点，点D不是[A，B]的3倍点，但点D是[B，A]的3倍点，根据这个定义解决下面问题：（1）在图1中，点A[C，D]的3倍点（填写“是”或“不是”）；[D，C]的3倍点是点（填写A或B或C或D）；（2）如图2，M、N为数轴上两点，点M表示的数是﹣3，点N表示的数是5，若点E是[M，N]的3倍点，则点E表示的数是；（3）若P、Q为数轴上两点，点P在点Q的左侧，PQ＝a，一动点H从点P出发，以每秒3个单位长度的速度沿数轴向右运动，设运动时间为t秒，求当t为何值时，点H恰好是P和Q两点的3倍点？（用含a的代数式表示）17．（2022秋•昆山市校级月考）如图所示，将连续的奇数1，3，5，7…排列成如下的数表，用十字形框框出5个数．探究规律一：设十字框中间的奇数为x，则框中五个奇数的和用含x的整式表示为，这说明被十字框框中的五个奇数的和一定是正整数p（p＞1）的倍数，这个正整数p是．探究规律二：落在十字框中间且位于第二列的一组奇数是15，27，39…，则这一组数可以用整式表示为12m+3 （m为正整数），同样，落在十字框中间且位于第三列的一组奇数可以表示为；（用含m的式子表示）运用规律（1）被十字框框中的五个奇数的和可能是625吗？若能，请求出这五个数，若不能，请说明理由．（2）请问（1）中的十字框中间的奇数落在第几行第几列？18．（2022秋•广陵区校级月考）从泰州乘“K”字头列车A、“T”字头列车B都可直达南京，已知A车的平均速度为80km/h，B车的平均速度为A车的1.5倍，且行完全程B车所需时间比A车少40分钟．（1）求泰州至南京的铁路里程；（2）若两车以各自的平均速度分别从泰州、南京同时相向而行，问经过多少时间两车相距40km？19．（2022秋•江都区月考）某地的一种绿色蔬菜，在市场上若直接销售，每吨利润为1000元，经粗加工后销售，每吨利润4000元，经精加工后销售，每吨利润7000元．当地一家公司现有这种蔬菜140吨，该公司加工厂的生产能力是：如果对蔬菜进行粗加工，每天可加工16吨，如果对蔬菜进行精加工，每天可加工6吨，但每天两种方式不能同时进行．受季节等条件的限制，必须用15天时间将这批蔬菜全部销售或加工完毕．为此，公司研制了三种方案：方案一：将蔬菜全部进行粗加工；方案二：尽可能地对蔬菜进行精加工，没来得及加工的蔬菜，在市场上直接出售；方案三：将一部分蔬菜进行精加工，其余蔬菜进行粗加工，并刚好15天完成．如果你是公司经理，你会选择哪一种方案，说说理由．20．（2023秋•锡山区期中）如图，数轴上有A、B、C、D四点，点D对应的数为x，已知OA＝5，OB＝3，CD＝2，P、Q两点同时从原点O出发，沿着数轴正方向分别以每秒钟a和b个单位长度的速度运动，且a＜b．点Q到点D后立即朝数轴的负方向运动，速度不变，在点C处与点P相遇，相遇后点P也立即朝着数轴的负方向运动，且P点的速度变为2a，Q点的速度不变．（1）P、Q两点相遇时，点P前进的路程为；Q、P两点相遇前的速度比＝；（用含有x的式子表示）（2）若点B为线段AD的中点，①此时，点D表示的数x＝；②相遇后，当点P到达点A处时，点Q在原点O的（填“左”或“右”）侧，并求出此时点Q在数轴上所表示的数字；（3）在（2）的条件下，当点P到达点A处时，立即掉头朝数轴的正方向运动，速度变为3a，点Q的速度始终不变，这两点在点M处第二次相遇，则点M在数轴上所表示的数字为．21．（2023秋•沭阳县校级月考）探索规律：将连续的偶2，4，6，8，…，排成如图：（1）十字框中的五个数的和与中间的数16有什么关系？（2）设中间的数为x，用代数式表示十字框中的五个数的和；（3）若将十字框上下左右移动，可框住另外的五位数，其它五位数的和能等于2010吗？如能，写出这五位数，如不能，说明理由．22．（2021秋•姑苏区校级期末）为增强公民节水意识，合理利用水资源，某市采用“阶梯收费”，标准如下表：用水量单价不超过6m3的部分2元/m3超过6m3不超过10m3的部分4元/m3超出10m3的部分8元/m3譬如：某用户2月份用水9m3，则应缴水费：2×6+4×（9﹣6）＝24（元）（1）某用户3月用水15m3应缴水费多少元？（2）已知某用户4月份缴水费20元，求该用户4月份的用水量；（3）如果该用户5、6月份共用水20m3（6月份用水量超过5月份用水量），共交水费64元，则该户居民5、6月份各用水多少立方米？23．（2021秋•惠山区期末）【探索新知】如图1，点C将线段AB分成AC和BC两部分，若BC＝πAC，则称点C是线段AB的圆周率点，线段AC、BC称作互为圆周率伴侣线段．（1）若AC＝3，则AB＝；（2）若点D也是图1中线段AB的圆周率点（不同于C点），则AC DB；（填“＝”或“≠”）【深入研究】如图2，现有一个直径为1个单位长度的圆片，将圆片上的某点与数轴上表示1的点重合，并把圆片沿数轴向右无滑动地滚动1周，该点到达点C的位置．（3）若点M、N均为线段OC的圆周率点，求线段MN的长度．（4）在图2中，若点D在射线OC上，且线段CD与图中以O、C、D中某两点为端点的线段互为圆周率伴侣线段，直接写出D点所表示的数．24．（2022秋•江都区校级月考）元旦期间，某商场打出促销广告（如下表）优惠条件一次性购物不超过200元一次性购物超过200元但不超过一次性购物超过500元500元优惠办法无优惠全部按9折优惠其中500元仍按9折优惠，超过500元部分按8折优惠小明妈妈第一次购物用了134元，第二次购物用了490元．（1）小明妈妈第一次所购物品的原价是元；（2）小明妈妈第二次所购物品的原价是多少元？（写出解答过程）（3）若小明妈妈将两次购买的物品一次性买清，可比两次购买节省多少元？25．（2022秋•梁溪区校级月考）在数轴上A点表示数a，B点表示数b，且a、b满足|a+2|+|b﹣4|＝0；（1）点A表示的数为；点B表示的数为；（2）如果M、N为数轴上两个动点，点M从点A出发，速度为每秒1个单位长度；点N从点B出发，速度为点A的3倍，它们同时向左运动，点O为原点．当运动2秒时，点M、N对应的数分别是、．当运动t秒时，点M、N对应的数分别是、．（用含t的式子表示）运动多少秒时，点M、N、O中恰有一个点为另外两个点所连线段的中点？（可以直接写出答案）26．（2022秋•兴化市校级月考）如图，已知A、B分别为数轴上的两点，A点对应的数为﹣20，B点对应的数为80．（1）请直接写出AB的中点M对应的数；（2）现在有一只电子蚂蚁P从A点出发，以2个单位/秒的速度向右运动，同时另一只电子蚂蚁Q恰好从B点出发，以3个单位/秒的速度向左运动，设两只电子蚂蚁在数轴上的C点相遇，请求出C点对应的数是多少；（3）若当电子蚂蚁P从A点出发时，以2个单位/秒的速度向右运动，同时另一只电子蚂蚁Q恰好从B 点出发，以3个单位/秒的速度向左运动，经过多长时间两只电子蚂蚁在数轴上相距25个单位长度？27．（2022秋•昆山市校级月考）在购买足球赛门票时，设购买门票张数为x（张），现有两种购买方案：方案一：若单位赞助广告费10000元，则该单位购买门票的价格为60元（总费用＝广告赞助费+门票费）．方案二：若购买的门票数不超过100张，每张100元，若所购门票超过100张，则超出部分按八折计算．解答下列问题：（1）方案一中，用含x的代数式来表示总费用为．方案二中，当购买的门票数x不超过100张时，用含x的代数式来表示总费用为．当所购门票数x超过100张时，用含x 的代数式来表示总费用为．（2）甲、乙两单位分别采用方案一、方案二购买本次足球赛门票，合计700张，花去的总费用计58000元，求甲、乙两单位各购买门票多少张？28．（2021秋•江都区期中）把2100个连续的正整数1、2、3、…、2100，按如图方式排成一个数表，如图用一个正方形框在表中任意框住4个数，设左上角的数为x．（1）另外三个数用含x的式子表示出来，从小到大排列是；（2）被框住4个数的和为416时，x值为多少？（3）能否框住四个数和为324？若能，求出x值，若不能，说明理由；（4）从左到右，第1至第7列各数之和分别为a1、a2、a3、a4、a5、a6、a7，求7个数中最大的数与最小的数之差．29．（2021秋•秦淮区期中）生活与数学：（1）吉姆同学在某月的日历上圈出2×2个数，正方形的方框内的四个数的和是32，那么第一个数是；（2）玛丽也在日历上圈出2×2个数，斜框内的四个数的和是42，则它们分别是；（3）莉莉也在日历上圈出5个数，呈十字框形，它们的和是50，则中间的数是；（4）某月有5个星期日的和是75，则这个月中最后一个星期日是号；（5）若干个偶数按每行8个数排成图4：①图中方框内的9个数的和与中间的数有什么关系：；②汤姆所画的斜框内9个数的和为360，则斜框的中间一个数是；③托马斯也画了一个斜框，斜框内9个数的和为252，则斜框的中间一个数是．30．（2021秋•洪泽区校级月考）请根据图中提供的信息，回答下列问题：（1）一个暖瓶与一个水杯分别是多少元？（2）甲、乙两家商场同时出售同样的暖瓶和水杯．为了迎接新年，两家商场都在搞促销活动．甲商场规定：这两种商品都打九折；乙商场规定：买一个暖瓶赠送一个水杯．若某单位想要买4个暖瓶和15个水杯，请问选择哪家商场购买更合算，并说明理由．。

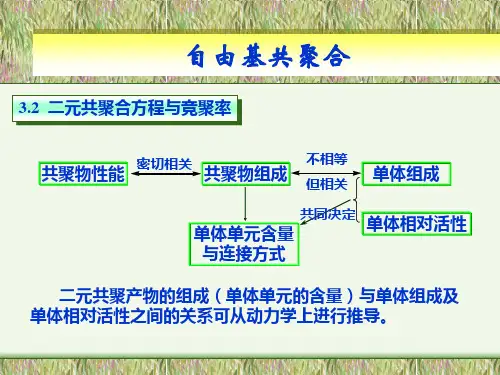
自由基共聚合练习题一、填空题：二、选择题：1.下列单体中，与丁二烯（e＝1.05）共聚时，交替倾向最大的是（）A.PS（e＝-1.08）B.马来酸酐(e＝2.25）C.醋酸乙烯（e＝-0.22）D.丙烯腈(e＝1.2)2.一对单体工具和的竞聚率r1和r2的值将随（）A．局和时间而变化 B.局和温度而变化 C.单体配比不同而变化 D.单体的总浓度而变化3.已知一对单体在进行共聚合反应时获得了恒比共聚物，其条件必定是（）A、r1=1.5,r2=1.5B、r1=0.1,r2=1.0C、r1=0.5,r2=0.5D、r1=1.5,r2=0.74.在自由基聚合中，竞聚率为（）时，可得到交替共聚物。

A5.下列共聚中，理想共聚是（），理想恒比共聚是（），交替共聚是（）A.r1r=1B.r1=r2=1C.r1=r2D.r1=r2=06.当r1＞1 r2＜1时，若提高聚合反应温度，反应将趋向于（）A 交替共聚B 理想共聚 C嵌段共聚 D恒比共聚7.当两种单体的Q.e值越接近则越（）A．越难共聚 B。

趋于理想共聚 C.趋于交替共聚 D.趋于恒比共聚8.两种单体的Q和e值越接近，就( )A.难以共聚B.倾向于交替共聚C.倾向于理想共聚D.倾向于嵌段共聚9.有机玻璃板材是采用( )A、本体聚合B、溶液聚合C、悬浮聚合D、乳液聚合三、概念题：1、共聚物2、自由基共聚合反应3、竞聚率4、理想恒比共聚5、Q，e概念四、论述题：1.按照大分子链的微观结构分类，共聚物分几类？它们在结构上有何区别？各如何制备？2.用动力学法推导共聚物组成方程所需作的假设？3.共聚物平均组成的控制？4.竞聚率的定义？说明其物理意义？如何根据竞聚率值判断两单体的相对活性？如何根据竞聚率值判断两单体是否为理想恒比共聚？5.简述几种典型竞聚率数值的意义，以r1 = k11 / k12为例r1 = 0， r1 = 1 ，r1 = ，r1 < 1， r1 > 1，6.在自由基共聚反应中，苯乙烯单体的相对活性远大于醋酸乙烯酯，若在醋酸乙烯酯均聚时加入少量苯乙烯将会如何？为什么?7.如何用Q,e概念判断两种聚合物的共聚倾向？8.Q-e概念？五、计算题：1.苯乙烯(M1)与丁二烯(M2)在5℃下进行自由基乳液共聚时，其r1=0.64，r2=1.38。

四川大学期末考试试题（2003——2004 下学期）课程号：课序号：课程名称：高分子化学任课教师：成绩：2 题间不留空，一般应题卷分开教务处试题编号：3 务必用A4纸打印学号：姓名：教务处试题编号：试卷A 答案及评分细则一、10分，每小题2分1、若干重复单元（或单体或结构单元）通过共价键连接起来，构成分子量大的一类化合物。

主要之点：“分子量大”2、体型缩聚进行到一定程度，突然出现粘度增大而不能流动的凝胶，这一过程叫凝胶化过程，出现凝胶时的反应程度，叫凝胶点 主要之点：“突然出现粘度增大而不能流动”3、i p RR v /= 只要符合这个表述式的叙述都是对的4、1211/k k r =凡是符合这个表达式的叙述都正确 5、橡胶分子间形成共价键的过程 关键在于“分子间成键”，这个概念也可以从性能角度解释。

二、10分，每小题2分，单体写错一个扣1分，原子数目不对扣0.5分。

1.n CH 2=CH ~[CH 2 CH]n ~ ~[CH 2 CH]n ~ （再纺丝）OH 聚合水解OCOCH 3OCOCH 3__O ～CH 2 CH CH 2 CH CH 2 CH ～OH CH 2+CH 2O_______缩醛化 2.n HOOCCOOH + n HO(CH 2)2OH __= OC CO O(CH 2)2O]n H + (2n 1) H 2 OHO[____1)或2）n HO(CH 2)2OOCC 6H 4COO(CH 2)2OH == HO(CH 2)2O[OCC 6H 4COO(CH 2)2O]n H+ (n –1) HO(CH 2)2OH 3. n HOOC(CH 2)8COOH + n H 2N(CH 2)6NH 2 =HO [OC(CH 2)8CO HN(CH 2)6NH ]n H + (2 n 1) H 2 O____4.C n HOOCH 3CH 3____OH +n Cl _C _Cl= C OCH 3CH 3O C ]n Cl + ( 2 n 1) HClH [O________5.OCN 3n + (n + 1) HO (CH 2)4OH =OCHN3O (CH 2)4O]n [ H ___HO(CH 2)4O三、50分，其中第6小题为2分，其余各小题均为3分。

有机合成知识总结目录目录前言有机合成的目的、宗旨和主要手段重要的有机反应研发常用的有机反应类型、机理和特点小结归纳和总结010203一、有机合成的目的通过一定的反应，使原来分子中某一个或几个化学键断裂，同时形成一个或几个新的化学键，从而使分子发生转变或将几个小分子连接起来。

二、有机合成的三条宗旨1.合成的步骤越少越好；2.每步的产率越高越好；3.原料和工艺成本越低越好。

三、有机合成的主要手段1.官能团的引入;2.官能团的转换；3.碳架的建造；①碳链的增长；②碳链的缩短；③碳架的重组；④环的闭合与打开。

目录目录前言有机合成的目的、宗旨和主要手段重要的有机反应研发常用的有机反应类型、机理和特点小结归纳和总结010203一．取代反应二．加成反应三．消除反应四．氧化还原反应五．缩合反应六．聚合反应一．取代反应1.亲核取代反应2.酯化反应3.酯的水解反应4.Friedel-Crafts反应5.环氧化合物的开环反应1.亲核取代反应化合物分子中的原子或原子团被亲核试剂取代的反应称为亲核取代反应。

在反应中，受试剂进攻的对象称为底物；亲核的进攻试剂称为亲核试剂；在反应中离开的基团称为离去基团；与离去基团相连的碳原子称为中心碳原子；生成物称为产物。

实例2.酯化反应酯化反应是一个可逆的反应，为了使正反应有利，通常采用的手段是：①使原料之一过量；②不断移走产物（例如除水）。

H+CH3COOH + C2H5OH CH3COOC2H5+ H2O 投料 1 ： 1 产率67%1 ：10 97%3.酯的水解反应（1）碱性水解OOC 2H 5CO 18C 2H 5 + H 2OCH 3CONa + C 2H 5O 18HNaOH慢快OORCOR '+ -OHRCOH + -OR'R-C-OR'OHO -反应机理RCO -ONa +RCONaO ROH +3.酯的水解反应（2）酸性水解H +CH 3COH + C 2H 5O 18HOCH 3CO 18C2H 5 + H 2OO4.Friedel-Crafts反应芳烃在路易斯酸催化下，苯环上的氢原子被烷基或酰基所取代的反应对甲苯磺酸5.环氧化合物的开环反应环氧类化合物的三元环结构使各原子的轨道不能正面充分重叠，而是以弯曲键相互连结，因此，分子中存在一种张力，极易与多种试剂反应，将环打开。

Q值Q值是衡量电感器件的主要参数。

是指电感器在某一频率的交流电压下工作时，所呈现的感抗与其等效损耗电阻之比。

电感器的Q值越高，其损耗越小，效率越高。

电感器品质因数的高低与线圈导线的直流电阻、线圈骨架的介质损耗及铁心、屏蔽罩等引起的损耗等有关。

Q value(一)共聚反应中单体和自由基的活性与结构有关，可用Q因子(单体共轭效应因子)和e因子(单体极性因子)描述。

为了求出Q值和e值，选定苯乙烯为参考单体，定其Q 值为1,e值为-0.8。

可由Q-e概念中的定量公式r1=k11/k12=Q1/Q2exp[-e1(e1-e2)] r1=k22/k21=Q2/Q1exp[-e2(e2-e1)]求得另一单体的Q和e值。

(二)核反应产物处于基态时的反应能。

对于核反应A(a,b)B来说，Q=(EB+Eb)-(Ea+EA)(三)Q值：是衡量电感器件的主要参数。

是指电感器在某一频率的交流电压下工作时，所呈现的感抗与其等效损耗电阻之比。

电感器的Q值越高，其损耗越小，效率越高。

电感器品质因数的高低与线圈导线的直流电阻、线圈骨架的介质损耗及铁心、屏蔽罩等引起的损耗等有关。

也有人把电感的Q值特意降低的，目的是避免高频谐振增益过大。

降低Q 值的办法可以是增加绕组的电阻或使用功耗比较大的磁芯。

影响Q值的因素Q值过大，引起电感烧毁，电容击穿，电路振荡。

Q很大时，将有VL=VC>>V的现象出现。

这种现象在电力系统中，往往导致电感器的绝缘和电容器中的电介质被击穿，造成损失。

所以在电力系统中应该避免出现谐振现象。

而在一些无线电设备中，却常利用谐振的特性,提高微弱信号的幅值。

品质因数又可写成Q=2pi*电路中存储的能量/电路一个周期内消耗的能量。

通频带BW与谐振频率w0和品质因数Q的关系为：BW=wo/Q,表明，Q大则通频带窄，Q小则通频带宽。

Q=wL/R=1/wRC 其中: Q是品质因素；w是电路谐振时的电源频率；L是电感；R是串的电阻；C是电容影响Q值的其它因素泛音次数表面抛光材料的杂质和缺陷安装应力焊接应力温度电极几何形状和类型片子的几何形状（外形、尺寸比）激励电平外壳中的气体（压力、气体种类）干扰模离子辐射近视手术中的Q值人眼的角膜在自然情况下不是一个理想的球面，而是中间凸、周边相对平坦的非球面，其作用是可以有效地消除球面像差（球差），从而更清晰成像。