当前位置：文档之家 › 8.4位移法的基本结构及位移法方程

8.4位移法的基本结构及位移法方程

  • 格式：ppt
  • 大小：264.56 KB
  • 文档页数：12

下载文档原格式

  / 12

合集下载

结构力学-位移法的典型方程及计算步骤

结构力学-位移法的典型方程及计算步骤

(e)
依题意可知并根据叠加原理上述条件可写为：
R1=R11+R12+R1P=r11 Z1+r12 Z2+R1P=0 R2=R21+R22+R2P=r21 Z1+r22 Z2+R2P=0
上述方程称为位移法基本方程，也称为位移法的典型方程。
为了求出典型方程的系数和自由项，可借助于表10-1，绘出基本
结构图，如下图10-7a,b, 和c所示。然后求出各系数和自由项。
r11 1 3i 4i
r12 6i1 0
R1P PL1 0
l
8
Z1=1
4i 1
2
6i 1l
2
Z2=1 1
2
3i M
3 2i 4
(a)
6i 3 l
3i 4 l
(b)
p
MP
PL 3
4
8
(C)
T10-7
1
2
r21 1
2
r22 1
6i l
0
12i
L2
3i
P
L2
2
2
R2P
0
系数和自由项可分为两类，分别由力矩平衡方程 M1=O求得为：

0
6 2 6 9 12 2 11 l Z1 l 2 Z2 16 P 0
Z1 0.02218 Pl Z2 0.02859 Pl 2
M M1Z1 M 2Z2 M P
转到下一节
者的原理有所不同。
§10-7 有侧移的斜柱刚架
B
B’
C’ C
C”
C
A
D
O A,D
B 结点位移图
O为极点,各结点位移前的位置

位移法的基本结构及位移法方程

位移法的基本结构及位移法方程
C D F1P C
b) M 1 图
D Z 1=1 k 11
c)
C
M图(kN· m)
D
(90) A -90 B C
F FQ CA = 45
(90) A EI 12 C EI 72 EI 12 D EI 72 k 11 B 225 A 135 B
D
F FQ DB=0
F1P
分别在MP图和 M 1 图中，截取两柱顶端以上部分为隔离体， F 0 如图8-17所示。由剪力平衡条件 ，得 x
Z
三、位移法方程
l/2 A Z1 FP l/2
l/2
FP l/2
C
F1=0
A
Z1 Z 1
C
Z1
EI =常数
l
FP F1=0 FP Z1 Z1 C A A Z 1Z Z1 Z1 1
F1P
P F1P
F
FP
C
C
A
A
C
EI =常数
B
l
B
B
B
B
B
c)
A
基本体系
F11 Z1
d)
F11 Z1 A Z1
C
锁住结点
M图
4i
重庆大学土木工程学院®
A
4i
C C EA =∞ D 例如，图8-16a所示刚架的基本未知量为结点 C、D D的水 平线位移Z1。在结点D加一附加支座链杆，就得到基本结构 EI EI （图8-16b）。其相应的基本体系如图8-16c所示，它的变形 和受力情况与原结构完全相同。 A B A B
k Z F 0 11 1 1P
这就是求解基本未知量Z1的位移法基本方程，其实质是平 衡条件 。 为了求出系数k11和自由项F1P，可利用表8-2和表8-1，在 基本结构上分别作出荷载作用下的弯矩图（MP图）和 Z1=1引起的弯矩图（ M 1 图）。

结构力学 位移法典型方程、计算举例

结构力学 位移法典型方程、计算举例
r11 B r12 CH
r21 B r22 CH R2
满足此方程，就消去了施加的2个约束
即，
r11 B r12 CH R1P 0 r21 B r22 CH R2 P 0
4）弯矩图的作法----消去最先附加的刚臂 P R1P R2P + MP图 R2
r
j 1
n
ij
Zj
，为消去该处的约束力，令： R iP
r
j 1
n
ij
Z j =0 即可。写成方程组的形式为：
r11 Z1 r12 Z 2 r1n Z n R1P 0 r Z r Z r Z R 0 21 1 22 2 2n n 2P rn1 Z1 rn 2 Z 2 rnn Z n RnP 0
R1P
R2P
+ +
r11 R A
1
r21R 2A
MP图 +
r12 B
r22 B
或
P
qL2/12
PL/8
4i
2i
q
R1P
R2P
+ A•
r11 8i r21 2i
2i
M 1图
MP图
4i
+
B•
4i r22 11i 2i r12 2i 3i 2i
M 2图
M M P M 1 A M 2 B
叠加右侧2个图，意味着结点B转动 及结点C侧移都发生。
叠加后B处的转角和C处的位移
分别为：B CH 则两处的约 束力必为R1，R2
r12 CH

8-3、8-4位移法的基本未知量和基本结构__典型方程及计算步骤解析

8-3、8-4位移法的基本未知量和基本结构__典型方程及计算步骤解析

§8.3 位移法的基本未知量和基本结构
确定独立的结点线位移另种一方法
（ 1）不考虑轴向变形 长度不变 (2) 弯曲变形微小，受弯矩
把原结构的所有刚结点和固定支座均改为铰结点→铰结体系，如图b。 此铰结体系为几何不变，原结构无结点线位移。 此铰结体系为几何可变或瞬变，添加最少的支座链杆保证其几何不变， 添加的链杆数目既是原结构独立的结点线位移数目。如图b，加一个水 平支座链杆，体系成为几何不变的。
上一章复习
等截面直杆的杆端弯矩和剪力
1 A
B A
2i
B
A B
4i
M AB 4i M BA 2i
A B 1 A
6i/l
FQ 6i / l
6i/l
B A
12i/l2
B
6i/l
M AB 6i / l M BA 6i / l
FQ 12i / l 2
等截面直杆的杆端弯矩和剪力
1 A A B A
+
2 EI i 2l
EI A l
1
B
3i/l
3i/l 3i/l
1
1
EI 2l
1
=
6
+
EI 3i 2 (2l ) 2l 6 EI 3i 2 (2l ) 2l
1
q A EI l B
ql 2 3
ql 2 6
1 1 q (2l ) 2 ql 2 8 2
§8.3 位移法的基本未知量和基本结构
附加刚臂： 阻止刚结点的转动，但不能阻止结点的移动。 附加支座链杆：阻止结点的线位移。
图a所示刚架，在刚结点1、3处分别加上刚臂，在结点3处加上一根 水平支座链杆，则原结构的每根杆件都成为单跨超静定梁。

[工学]位移法

[工学]位移法

[ e ] B
(b)
b M F Q B A
单元刚度方程——单元杆端力和杆 端位移的关系式。
推导单元刚度方程思 路及方法：
方法1
已知梁的两端固定支座发生位移A、 B、，求杆端力FQAB、MAB、FQBA、 MBA。推导是求超静定梁在支座移动 时的支座反力（杆端力）的过程，直 接由力法计算。
方法 2
已知简支梁两端作用有集中外力偶 MAB、MBA，同时B支座有支座位移， 用单位荷载法求位移A、B，然后将 杆端力FQAB、MAB、FQBA、 MBA表示成 位移的函数形式。推导是对静定梁在 荷载和支座移动下，求梁两端转角位 移的过程。
按方法2建立单元刚度方程
M A B A M B A B B `
FQAB FQBA
6 EI 6 EI 12 EI 2 A 2 B 3 L L L
(9-2-1a)
4）当考虑典型单元上同时也作用荷 载时的单元刚度方程
M A B A
A E IL
(a)
[e]
B B `

F Q A B

F M B A
F M A B
B
(b)
4 EI 2 EI 6 EI F M AB A B 2 M AB L L L 2 EI 4 EI 6 EI F M BA A B 2 M BA L L L
EI0=
L
EI
EI
(a)
L
z1 EI0=
z1
EI
EI
(b)
解 1)确定位移法基本未知量
6i 2) M AB M BA z1 L 2 6i qL M CD z1 L 12 2 6i qL M DC z1 L 12

8-3、8-4位移法的基本未知量和基本结构__典型方程及计算步骤

8-3、8-4位移法的基本未知量和基本结构__典型方程及计算步骤

§6.2.1 位移法的基本未知量
3
2
1
结点转角的数目：7个
独立结点线位移的数目：3个
§8.3 位移法的基本未知量和基本结构
图a所示刚架，结点线位移数目=2
图b所示刚架，结点角位移数目=2 结点线位移数目=2
§8.3 位移法的基本未知量和基本结构
确定角位移6个
确定线位移2个
§8.3 位移法的基本未知量和基本结构
图a所示刚架，结点角位移数目=4（注意结点2）
结点线位移数目=2
加上4个刚臂，两根支座链杆，可得基本结构如图b。
§6.2.1 位移法的基本未知量
1
2
1
1
2

3
§6.2.1 位移法的基本未知量
例1.
B
C
例2.
B
C
A 只有一个刚结点B，由于忽 略轴向变形，B结点只有 B
A
只有一个刚结点B， 由于忽略轴向变形及C 结点的约束形式，B结 点有一个转角和水平位 移 B BH
2kN/m 16kN
A
i
6m
B
3m
i
3m 16kN
Z1
C
2kN/m
A
B
C
解 （1）选取基本体系。
（2）建立位移法典型方程。
r11Z1 R1 0
（3）求系数和自由项。
4i
Z1=1
r11
A
2i
B
3i 18 6
M 1图
C
4i
3i
6
R1P
A
B
MP图（kN.m）
C
6
18
r11 4i 3i 7i
典型方程

位移法典型方程计算举例

位移法典型方程计算举例

n
n
rijZj ， 为 消 去 该 处 的 约 束 力 ， 令 ： R iP rijZj=0即 可 。 写 成 方 程 组 的 形 式 为 ：
j 1
j 1
r11Z1 r12Z2 r1n Zn R1P 0
r21
Z1
r22Z2
r2n
Zn
R2P
0
rn1Z1 rn2 Z2 rnnZn RnP 0
这就是位移法的典型方程。
R2P +
MP图
r11R1 A
r2R12A
+
rr2111AArr12
2B 2B
R1 R2
r12B r22B
rr2111AArr1222B BR R12PP00 这就是位移法方程，解出θA，θB
5）ri j的求法
2i 4i
r11 8i r212i
2i
M
图
1
4i 4i 2i r12 2i 3ir22 11i
2i
M
图
2
求r11,r12的研究对象
求r21,r22的研究对象
6）弯矩图的作法
qL2/12
q
P R1P
PL/8
R2P
MP图
++
r11R1 A
r2R12A
+
r12B r22B
即 M M P M 1A M 2B
qL2/12
q
P R1P
PL/8
R2P
4i
+ A•
MP图
2i + B•
2i
r11
r21
2i
M
图
1
4i
4i
r12

结构力学 第8章 位移法

结构力学 第8章 位移法

6
杆端内力、位移的符号规定： 杆端内力、位移的符号规定：
●
杆端弯矩: 表示AB杆 端的弯矩 绕杆端顺时针 端的弯矩。 顺时针为正 杆端弯矩: MAB表示 杆A端的弯矩。绕杆端顺时针为正 杆端剪力：绕隔离体顺时针转为正(同前) 杆端剪力：绕隔离体顺时针转为正(同前)。 顺时针转为正 结点转角： 顺时针转为正。 结点转角：以顺时针转为正。 转为正 杆端的相对线位移：使杆件弦转角顺时针转动为正。 杆端的相对线位移：使杆件弦转角顺时针转动为正。 弦转角顺时针转动为正
1 2 3
杆14, 36: 两端固定
4 5 6
基本未知量3个。 基本未知量 个
杆12, 23, 25: 一端固定 一端铰结
23
又例:
m m
原结构
次超静定） （4次超静定） 次超静定
基本结构
次超静定） （5次超静定） 次超静定
24
§8—4 位移法的典型方程及计算步骤 4
基本未知量为: 基本未知量为:Z1、Z2 。 基本结构如图。 基本结构如图。 R1—附加刚臂上的反力矩 附加刚臂上的反力矩 F R2—附加链杆上的反力 附加链杆上的反力 l 据叠加原理, 则有 据叠加原理, 2 R1=R11+R12+R1P=0 R2=R21+R22+R2P=0
EI
可见， 不独立, 代入第一式: 可见，B=f (A、△AB), 不独立 代入第一式 MAB=3iA 式中 （转角位移方程） 转角位移方程） （固端弯矩） 固端弯矩）
l
t2
16
§8—3 位移法的基本未知量和基本结构 3
1.位移法的基本未知量 1.位移法的基本未知量
位移法的基本未知量是各结点的角位移和线位移, 位移法的基本未知量是各结点的角位移和线位移, 计算时应 各结点的角位移 独立的角位移和 数目。 首先确定独立的角位移 线位移数目 首先确定独立的角位移和线位移数目。 (1) 独立角位移数目 同一刚结点,各杆端转角相等一个独立的角位移未知量。 一个独立的角位移未知量 同一刚结点,各杆端转角相等一个独立的角位移未知量。 固定支座处，转角=0,已知量; =0,已知量 固定支座处，转角=0,已知量; 铰结点或铰支座各杆端的转角不独立，不必作为基本未知量。 铰结点或铰支座各杆端的转角不独立，不必作为基本未知量。 独立角位移数目= 独立角位移数目=结构刚结点的数目

位移法读书笔记

位移法读书笔记

【读数笔记xxx】第8章8.1 位移法的基本概念位移法与力法的基本区别：1.力法以多余未知力（支反力或内力）为基本未知量，位移法以结点的独立位移（角位移或线位移）为基本未知量。

2.力法是把超静定结构拆成静定结构(即基本结构)，作为其计算单元，而位移法则是把结构拆成杆件，作为其计算单元。

位移法分析中需要解决的三个问题：1.确定杆件的杆端内力与杆端位移及荷载之间的函数关系（即杆件分析或单元分析）2.选取结构上哪些结点位移作为基本未知量。

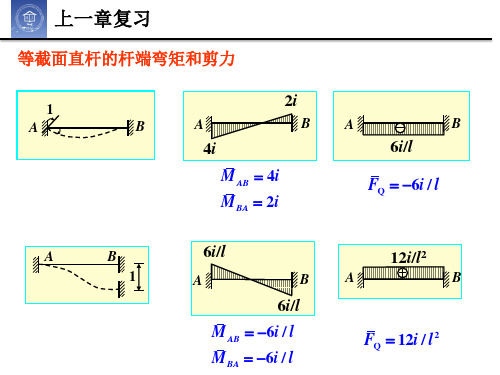
3.建立求解这些基本未知量的位移法方程（即整体分析）8.2等截面直杆的转角位移方程由8.1可以知道，位移法的计算单元是杆件，所以位移法首先应确定杆件的杆端内力与杆端位移及荷载之间的函数关系(杆件的转角位移方程)。

杆端内力正负号的规定：杆端弯矩对杆端而言，以顺时针方向为正，反之为负。

对结点或支座而言，则以逆时针方向为正，反之为负。

杆端剪力和杆端轴力的正负号规定，仍与前面规定相同。

杆端位移的正负号规定：角位移以顺时针为正，反之为负。

线位移以杆的一端相对于另一端产生顺时针方向转动的线位移为正，反之为负。

由杆端单位位移引起的杆端内力称为形常数。

i=EI/l，称为杆件的线刚度。

由荷载或温度变化引起的杆端内力称为载常数。

其中的杆端弯矩也常称为固端弯矩，用表示；杆端剪力也常称为固端剪力，用表示。

转角位移方程：应用以上三组转角位移方程，即可求出三种基本的单跨超静定梁的杆端弯矩。

至于杆端剪力，则可根据平衡条件导出为：对上述三种基本的单跨超静定梁的杆端剪力表达式，也可根据叠加原理，写出如下：8.3位移法的基本未知量位移法选取结点的独立位移，包括结点的独立角位移和独立线位移，作为其基本未知量，并用广义位移符号Zi表示。

、位移法基本未知量的总数目（记作n）等于结点的独立角位移数（记作ny）与独立线位移数（记作nl）之和，即n=ny+nl结点独立角位移数（ny）一般等于刚结点数加上组合结点（半铰结点）数，但须注意，当有阶形杆截面改变处的转角或抗转动弹性支座的转角时，应一并计入在内。

结构力学 位移法

结构力学 位移法
16kN A EI B EI D 3m EI C 2kN/m
A EI B EI C 16kN 2kN/m
6m
EI
D
3m
6m
基本结构 基本方程：k11 △1＋F1P＝0 F1P
24 18
解：基本未知量：△1=θB， k11 4i 3i i
12
2i
△1= 1； M 图 MP图
k11
4i
3i i 2i
F1P
A B
F2P 16kN.m
C 8kN.m
F1P
6kN.m B 4kN.m 4kN.m
F2P
C 16kN.m
F1P = 2kN.m
F1P = -12kN.m
四、解题步骤(以一个基本未知量为例)
⑴确定基本未知量△1、基本结构、基本方程； ⑵令△1=1，画基本结构的弯矩 M 1 图，由结点或截面平衡方 程得系数k11； ⑶画基本结构荷载下的弯矩MP图，由结点或截面平衡方程得 常数项F1P； ⑷将系数k11 和常数项F1P 代入基本方程k11 △1 ＋ F1P ＝0，求 解基本未知量△1 ；
⑴ 基本方程中系数kij的确定 系数kij为第j号位移△j=1，第i号附加约束的约束反力，也就 是结构的刚度系数。由结点或截面的平衡方程确定之。 附加约束的约束反力kij的正负规定与结点位移△j的正负规定 相同，刚臂的约束反力(约束力偶)kij以顺时针转为正，链杆的约 束反力kij以使杆顺时针转为正。 位移法中规定：杆端弯矩也以顺时针转为正。
△ Dx
D
△ Ex
E
△1=θ
F
F
P
△Fx
F A
θ
△2= △Dx= △Ex
△ Gx
G
F

《结构力学》第八章-位移法

《结构力学》第八章-位移法

(5) 按叠加法绘制最后弯矩图。
18
例 8—1 图示刚架的支座A产生了水平位移a、竖向位移b=4a
及转角=a/L，试绘其弯矩图。
L
解：基本未知量 Z 1(结点C转角)； C EI
B C Z1
B
基本结构如图示；
2EI
建立位移法典型方程： r11Z1+R1△=0
A Z1
基本结构 A
为计算系数和自由项，作
链为了杆能数简，捷即地为确定原出结结构构的的独独立立线线位
(b)
移位移数数目目(见，可图以b)。
11
2.位移法的基本结构
用位移法计算超静定结构时，每一根杆件都视为一根单跨超静
定梁。因此，位移法的基本结构就是把每一根杆件都暂时变为一根
单跨超静定梁(或可定杆件)。通常 的做法是，在每个刚结点上假想 1
构在荷载等外因和各结点位移共同作用下，各附加联系上的反力矩
或反力均应等于零的条件，建立位移法的基本方程。
(3) 绘出基本结构在各单位结点位移作用下的弯矩图和荷载作
用下(或支座位移、温度变化等其它外因作用下)的弯矩图，由平衡
条件求出各系数和自由项。
(4) 结算典型方程，求出作为基本未知量的各结点位移。
正。
B
B
B′
X2
X3
M1图
1
M
图
2
7
将以上系数和自由项代入典型方程，可解得 X1=
X2=
令
称为杆件的线刚度。此外，用MAB代替X1，用
MBA代替X2，上式可写成
MAB= 4iA+2i B－ MBA= 4i B +2i A－
(8—1）
是此两端固定的梁在荷载、温度变化等外因作用下的杆

结构力学第8章

结构力学第8章

(h)
1 1 ∆ AB ′ θ A = θ A +θ ′′ = M AB − MBA + 3i 6i l (c) 1 1 ∆ AB ′ θ B = θ B +θ ′′ = − M AB + MBA + 6i 3i l
(2) B端为定向支承，如图(d)所示。 B端为定向支承 如图(d)所示。 端为定向支承， (d)所示
1. 位移法的基本未知量的数目(至少要求出多少个位 位移法的基本未知量的数目( 移未知量) 移未知量) 2. 单跨超静定梁分析 相应于基本未知量的位移法方程如何建立和求解。 3. 相应于基本未知量的位移法方程如何建立和求解。
在本节中，我们讨论第一个问题， 在本节中，我们讨论第一个问题，位移法的基本未 知量的数目及相应的位移法基本结构。其它两个问题， 知量的数目及相应的位移法基本结构。其它两个问题， 后面讨论。 后面讨论。 为了将原刚架的各杆变成单跨超静定梁， 为了将原刚架的各杆变成单跨超静定梁，可以在原 刚架的结点上引入某些附加约束 刚架的结点上引入某些附加约束 如：附加的刚臂（阻止结点转动的约束） 附加的刚臂（阻止结点转动的约束） 附加链杆（阻止结点线位移的约束） 附加链杆（阻止结点线位移的约束） 引入附加的刚臂 附加链杆后 使得结构的结点 附加的刚臂或 结点变 引入附加的刚臂或附加链杆后，使得结构的结点变 固定端或铰支端，而各杆成为单跨超静定梁。 成固定端或铰支端，而各杆成为单跨超静定梁。所得的 结构即为位移法计算时的基本结构 位移法计算时的基本结构。 结构即为位移法计算时的基本结构。 而结构独立的基本未知量数目等于把原结构转变为 独立的基本未知量数目 而结构独立的基本未知量数目等于把原结构转变为 基本结构时， 附加的刚臂和附加链杆数目之和 数目之和。 基本结构时，所附加的刚臂和附加链杆数目之和。这样 在确定了基本结构的同时， ，在确定了基本结构的同时，也就确定了位移法的基本 未知量的数目。 未知量的数目。如：

位移法典型方程、计算举例资料

位移法典型方程、计算举例资料

n
n
rijZj ， 为 消 去 该 处 的 约 束 力 ， 令 ： R iP rijZj =0即 可 。 写 成 方 程 组 的 形 式 为 ：
j 1
j 1
r11Z1 r12Z2 r1n Zn R1P 0
r21
Z1
r22Z2
r2n
Zn
R2P
0
rn1Z1 rn2 Z2 rnnZn RnP 0
六、位移法计算应注意的问题
1. 位移法过程中，判断一个杆件有无弯矩的方法是： 1）该杆有无杆端转角 2）该杆有无杆端相对侧移 3）该杆上有无荷载作用
2. 各图中R1P，r11，r12 的方向应保持一致画出 R2P，r21，r22的方向应保持一致画出
3. r11，r22 均为大于零的值，即施加的单位力与发 生位移的方向协调一致。
这就是位移法的典型方程。
五、位移法的计步骤
1. 确定位移法变量 2. 作MP图，求出R1P、R2P
3 .作 M 1 、 M 2 图r ， 1， 1r2， 1 求 r1， 2r22
4.写出位移法方,程 并求解
rr2111ZZ11rr1222ZZ22
R1P 0 R2P 0
5.依 MM PM 1Z1M 2Z2作出弯矩图
位移法典型方程、计算举例 资料
3、求解思路： “先修改，后复原”
A
B
1）位移法变量
A,B

2）附加2个刚臂，使结点不能转动----各杆弯矩不能相互传递 PL/8
qL2/12
R1P
R2P
R1P，R2P怎么求？
MP图
3）如何消掉附加的刚臂约束？
若令 R1= - R1P、R2= - R2P
P
PL/8

8.4 位移法的基本结构及位移法方程

8.4 位移法的基本结构及位移法方程
8.4
位移法的基本结构及位移法方程
一、位移法的基本结构 位移法的基本结构就是通过增加附加约束（ 位移法的基本结构就是通过增加附加约束（包括附加刚 臂和附加支座链杆） 得到的三种基本超静定杆的综 臂和附加支座链杆）后，得到的三种基本超静定杆的综 合体。 合体。 所谓附加刚臂， 所谓附加刚臂，就是在每个可能发生独立角位移的刚结 点和组合结点上， 点和组合结点上，人为地加上的一个能阻止其角位移 (但并不阻止其线位移 的附加约束，用黑三角符号“ ” 但并不阻止其线位移)的附加约束 但并不阻止其线位移 的附加约束，用黑三角符号“ 表示。 表示。 所谓附加支座链杆， 所谓附加支座链杆，就是在每个可能发生独立线位移 的结点上沿线位移的方向， 的结点上沿线位移的方向，人为地加上的一个能阻止 其线位移的附加约束。 其线位移的附加约束。
F1P = FQFCA + FQFDB = 45 + 0 = 45 kN
All Rights Reserved 重庆大学土木工程学院
C
D
F1P
C
D
Z 1=1 k 11
C
D
(90) A -90 B C
F FQCA = 45
(90) A EI 12 C EI 72 EI 12 D EI 72 k 11 B 225 A 135 B
F1P A
FP C
c)
B
基本体系
B
d)
锁住结点
F11
基本结构在结点位移Z 基本结构在结点位移 1和荷 载共同作用下， 载共同作用下，刚臂上的反 力矩F1必定为零 必定为零（ ）。 力矩 必定为零（图c）。
Z1 A Z1 Z1
C
F1 = F11 + F1P = 0

结构力学课件位移法典型方程

结构力学课件位移法典型方程
第六章 位移法
6.3 位移法的典型方程
Canonical equations of displacement method
1. 位移法基本方程的建立
两种途径： 典型方程法：将杆端力视为各影响因素单独作用效果的 叠加，由此借助平衡条件建立位移法方程。（讲授）
直接平衡法：直接利用转角位移方程，按照结点或截面 的平衡条件建立位移法方程。（自学）
······ rn1Z1 + r n2Z2 + ···+ rnnZn + RnP = 0
可用矩阵表示为：[r]{Z} +{RP} = {0}
位移法方程的物理意义： 基本结构在荷载和结点位移作用下，附加约束反力等于零。
[r]{Z} +{RP} = {0}
式中： rii 为基本结构仅在单位结点位移Zi =1单独作用时，在附加约束 i 中产生的约束力; rij 为基本结构仅在单位结点位移Zj =1单独作用时，在附加约束 i 中 产生的约束力（i≠j） RiP 为基本结构在荷载单独作用（结点位移都锁住）时，在附加约 束 i 中产生的约束力
EI Z2
FP
EI
EA
l
2EI EI l
l
r21
3i/l
12i/l
12i/l
3i/l
Z2=1
Z1=1 r22
r11
3i
M1
4i
Z1 r11Z1 r12Z2 R1P 0 r21Z1 r22Z2 R2P 0
r12
M2
R2P FP
R1P
MP
0.24FPl
M
0.39FPl 0.13FPl
r11 30i / l 2
10kNm
2EI

结构力学位移法

结构力学位移法

第十七章位移法求解超静定结构的两种最基本的方法力法适用性广泛，解题灵活性较大。

（可选用各种各样的基本结构）。

位移法在解题上比较规范，具有通用性，因而计算机易于实现。

位移法可分为：手算——位移法电算——矩阵位移法力法位移法力法与位移法最基本的区别：基本未知量不同力法：以多余未知力基本未知量位移法：以某些结点位移基本未知量F PϕBϕB在忽略杆轴向变形和剪切变形的条件下，结点B 只发生角位移ϕB 。

由于结点B 是一刚结点，故汇交于结点B 的两杆的杆端在变形后将发生与结点相同的角位移。

位移法计算时就是以这样的结点角位移作为基本未知量的。

第一节位移法的基本概念BAClhEI 1EI 2首先，附加一个约束使结点B 不能转动，此时结构变为两个单跨超静定梁。

称为位移法的基本结构。

在荷载作用下，可用力法求得两根杆的弯矩图。

由于附加约束阻止结点B 的转动，故在附加约束上会产生一个约束力矩1631l F F P P -=C BAF P316Fl 532FlCAB然后，为了使变形符合原来的实际情况，必须转动附加约束以恢复ϕB 。

两个单跨超静梁在B 端有角位移时的弯矩图，同样可由力法求得。

此时在附加约束上产生约束力矩Bh EI lEI F ϕ⎪⎭⎫ ⎝⎛+=211143ϕB ϕBBA CB lEI ϕ13B h EI ϕ24B hEI ϕ22F PBAC求基本未知量,可分两步完成：1）在可动结点上附加约束，限制其位移，在荷载作用下，附加约束上产生附加约束力；2）转动附加约束使结点产生角位移ϕB ，使结构发生与原结构一致的结点位移。

ϕBϕB附加刚臂经过上述两个步骤，附加约束上产生约束力矩应为F 11和F 1P 之和。

由于结构无论是变形，还是受力都应与原结构保持一致，而原结构在B 处无附加约束，亦无约束力矩，故有F 11+F 1P ＝001634321=-⎪⎭⎫⎝⎛+Fl h EI lEI B ϕ解方程可得出ϕB 。

位移法典型方程将求出后ϕB ，代回图22-1c ，将所得的结果再与图22-1b 叠加，即得原结构（图22-1a ）的解。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
8.4 位移法的基本结构及位移法方程
一、位移法的基本结构
位移法的基本结构就是通过增加附加约束（包括附 加刚臂和附加支座链杆）后，得到的三种基本超静定杆 的综合体。
所谓附加刚臂，就是在每个可能发生独立角位移的 刚结点和组合结点上，人为地加上的一个能阻止其角位 移(但并不阻止其线位移)的附加约束，用黑三角符号 “ ”表示。
D Z1=1 k11 C
D
(90)
(90)
A -90
B
A
B
A
B
EI 12
EI 12
225
135
C
D
F1P
C
D
k11
FQFCA=45
FQFDB=0
EI 72
EI 72
分别在MP图和 M 1 图中，截取两柱顶端以上部分为隔离体，
如图8-17所示。由剪力平衡条件
Fx ，0得
F1P
FF QCA
FF QDB
45 0 45 kN
k11 8i
F1P
1 8
FP l
k11Z1 F1P 0
将k11和F1P的值代入上式，解得
Z1
F1P k11
FP l 64i
结果为正，表示Z1的方向与所设相同。结构的最后弯矩可由 叠加公式计算，即
M M1Z1 M P
M BA 2i
0 5FPl / 32
M
M
M
AB AC CA
所谓附加支座链杆，就是在每个可能发生独立线 位移的结点上沿线位移的方向，人为地加上的一个能 阻止其线位移的附加约束。
All Rights Reserved
重庆大学土木工程学院®
Z1 Z4
F
G
H
F
Z2
Z3 Z3
C
D
E
C
Z3
A
B
A
G
H
D
E
B
a) 原结构及其基本未知量
b) 基本结构
All Rights Reserved
B
B
l l
l
l/2 FP l/2
A
C
Z1
Z1
F1=0
A
ZA1
A
FP l/2
FP l/2
CC C
F1P A
Z1
ZZ11 Z1
F1F=P0
FP
Z1 C
C
A
Z1
Z1
FF111P Z1 AA Z1
EI =常数
EI =常数
B
BB B
B
B
BB
aA) 原结构C
All Rights Reserved
b) 基本结构F11
2i
16
16
FP l
C
16 A
C
9FP l 64
B
B 2i
B FPl 32
F1P
A
FP l 8
k11 A 4i
4i
在图 M1 中取结点A为隔离体，由 M A 0 ，得
在MP图中取结点A为隔离体，由 M A 0 ，得
刚臂内之反力矩以顺时针为正
All Rights Reserved
重庆大学土木工程学院®
Z1
1620 EI
结构的最后弯矩图可由叠加公式M M1Z1 M P 计算后绘 制，如图c所示。
A
C
Z1
A
Z1
Z1
重庆大学土木工程学院®
c)
基本体系 F11C源自Z1AZ1Z
三、位移法方程
l/2 FPl/l2/2 FP l/2
AA
C
C
Z1
ZZ11
Z1
EI =常数EI =常数
l l
F1=0 F1=0FP
FP F1P
Z1
Z1 C
C
A
A
A
Z1
Z 1Z 1
Z1
FF1PP
FP
C
C
A
B
B
B
B
B
B
c) 基本体系
重庆大学土木工程学院®
二、位移法的基本体系
l/2 FP l/2
F1=0
FP
F1P
图a所示刚架的基本Z1A未知Z1 量为结C 点A的转Z1角A ZZ1Z11。在结C 点 A
A加一附加刚臂，就得到位移EI法=常的数 基本结构（图b）。同力
法一样，受荷载和基本未知量共同作用的基本结构，称为
B
基本体系（图c）。
4i 4i 2i
FPl 64i
0
FFPPl
l /
/ 8
8
FPl /16
5FFPPll//3126
All Rights Reserved
重庆大学土木工程学院®
M BA 2i
0 5FPl / 32
M
M
M
AB AC CA
4i 4i 2i
FPl 64i
0
FFPPl
l /
A
B
Z1
Z1
C
EA=∞ D
EI
EI
C
D
C
D
Z1 F1=0
6m 20kN/m
20kN/m
A
B
位移法方程
All Rights Reserved
A
B
基本结构
A
B
基本体系
C
D
Z1 F1=0
k11Z1 F1P 0
20kN/m
重庆大学土木工程学院®
A
B
a) MP图(kN·m)
C
D
F1P
b) M 1图
C
c) M图(kN·m)
C
9FP l 64
B FPl 32
M图
例如，图8-16a所示C刚Z1 架EA的=∞ 基D 本Z1 未知量为C结点C、DD的水
20kN/m 6m
平线位移Z1。在结点D加E一I 附加E支I 座链杆，就得到基本结构 （图8-16b）。其相应的基本体系如图8-16c所示，它的变形
和受力情况与原结构完全A 相同。B
/ 8
8
FPl /16
5FFPPll//3126
FP l F1P 8
A
FP l
FP
8
C
FP l 8
B
FM1P P图
All
Rights
A
Reserved
FP l 8
k11 Z1=1
2i
A
4i
C
4i
B 2i
M 图 k11 1 重庆大学土A木工程学4i院®
4i
FP l
FP l
16
16
FP l
16 A
式中，Fij表示广义的附加反力矩（或反力），其中第一个 下标表示该反力矩所属的附加约束，第二个下标表示引起 反力矩的原因。设k11表示由单位位移Z1=1所引起的附加刚 臂上的反力矩，则有 F11=k11Z1，代入上式，得
k11Z1 F1P 0
这就是求解基本未知量Z1的位移法基本方程，其实质是平 衡条件 。
为了求出系数k11和自由项F1P，可利用表8-2和表8-1，在 基本结构上分别作出荷载作用下的弯矩图（MP图）和
Z1=1引起的弯矩图（ M1 图）。
All Rights Reserved
重庆大学土木工程学院®
FP l F1P 8
A
FP l
FP
8
C
FP l 8
k11 Z1=1 A
4i
4i
FP l
FP l
All Rights Reserved
重庆大学土木工程学院®
C
D
F1P
C
D Z1=1 k11 C
D
(90)
(90)
A -90
B
A
B
A
B
EI 12
EI 12
225
135
C
D
F1P
C
D
k11
FQFCA=45
FQFDB=0
EI 72
EI 72
k11
EI 72
EI 72
EI 36
将k11和F1P的值代入位移法方程式，解得
d)
F11
A
C
基本A 结构在结C 点位移Z1和荷载
共同作用下，刚臂上的反力矩F1必
Z1 A
F11 Z1 C
Z1
Z1 A
Z1
Z1
锁住结点
C
定为零（图c）。
B B
F1 F11 F1P 0
B B
e) 放松结点
All Rights Reserved
重庆大学土木工程学院®
F1 F11 F1P 0