下载文档原格式
【读数笔记xxx】第8章8.1 位移法的基本概念位移法与力法的基本区别：1.力法以多余未知力（支反力或内力）为基本未知量，位移法以结点的独立位移（角位移或线位移）为基本未知量。
2.力法是把超静定结构拆成静定结构(即基本结构)，作为其计算单元，而位移法则是把结构拆成杆件，作为其计算单元。
位移法分析中需要解决的三个问题：1.确定杆件的杆端内力与杆端位移及荷载之间的函数关系（即杆件分析或单元分析）2.选取结构上哪些结点位移作为基本未知量。
3.建立求解这些基本未知量的位移法方程（即整体分析）8.2等截面直杆的转角位移方程由8.1可以知道，位移法的计算单元是杆件，所以位移法首先应确定杆件的杆端内力与杆端位移及荷载之间的函数关系(杆件的转角位移方程)。
杆端内力正负号的规定：杆端弯矩对杆端而言，以顺时针方向为正，反之为负。
对结点或支座而言，则以逆时针方向为正，反之为负。
杆端剪力和杆端轴力的正负号规定，仍与前面规定相同。
杆端位移的正负号规定：角位移以顺时针为正，反之为负。
线位移以杆的一端相对于另一端产生顺时针方向转动的线位移为正，反之为负。
由杆端单位位移引起的杆端内力称为形常数。
i=EI/l，称为杆件的线刚度。
由荷载或温度变化引起的杆端内力称为载常数。
其中的杆端弯矩也常称为固端弯矩，用表示；杆端剪力也常称为固端剪力，用表示。
转角位移方程：应用以上三组转角位移方程，即可求出三种基本的单跨超静定梁的杆端弯矩。
至于杆端剪力，则可根据平衡条件导出为：对上述三种基本的单跨超静定梁的杆端剪力表达式，也可根据叠加原理，写出如下：8.3位移法的基本未知量位移法选取结点的独立位移，包括结点的独立角位移和独立线位移，作为其基本未知量，并用广义位移符号Zi表示。
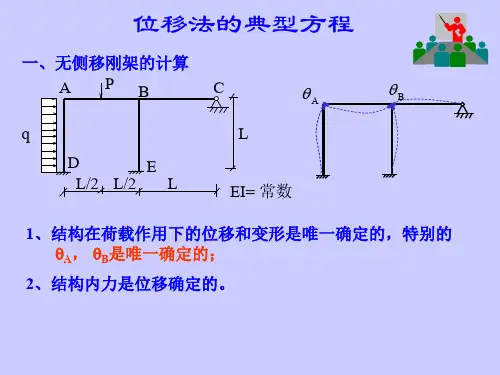
、位移法基本未知量的总数目（记作n）等于结点的独立角位移数（记作ny）与独立线位移数（记作nl）之和，即n=ny+nl结点独立角位移数（ny）一般等于刚结点数加上组合结点（半铰结点）数，但须注意，当有阶形杆截面改变处的转角或抗转动弹性支座的转角时，应一并计入在内。
位移法位移法也是计算超静定结构的基本方法。
位移法是以结构的结点位移（结点角位移和结点线位移）作为基本未知量，通过平衡条件建立位移法方程，求出位移后，即可利用位移和内力之间的关系，求出杆件和结构的内力。
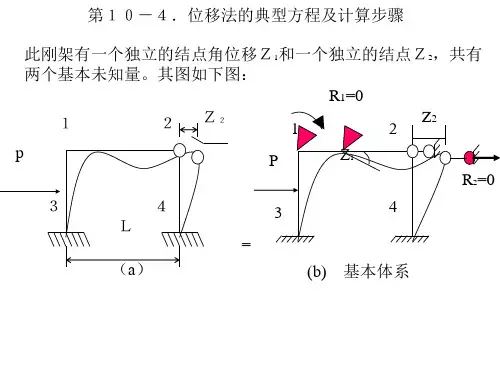
在位移法求解超静定问题中，有七大步骤：第一步：分析结构体系（是否为几何不变体系，是否有结点位移），结构体系中的结点位移（结点角位移和结点线位移）就是结构的所求的基本未知量。
第二步：选取基本结构，即在原结构中的基本未知量（结点角位移和结点线位移）处加上约束（刚臂和链杆），均假设顺时针转动。
第三步：列位移法方程：01111=+P R Z r （一个结点位移未知量）当为n 次超静定时，0022112222212111212111=++++=++++=++++nP n nm n n P n n P n n R Z r Z r Z r R Z r Z r Z r R Z r Z r Z r第四步：画P M M 、1图，求nP nm R r 、（画P M M 、1图，通过查表得出，注意形常数及载常数的查法，记住是以顺时针转动为正。
）第五步：求解未知位移n Z 。
第六步：求杆端弯矩：P R Z M M +=11（一结点位移未知量）P n n i i R Z M Z M Z M Z M M ++++++= 2211（n 个结点位移未知量）此步骤的正负号规定容易与力法正负号规定混淆。
在位移法中，杆端弯矩以顺时针转动为正，逆时针转动为负。
第七步：求跨中弯矩（针对于集中力作用在跨中处以及均布荷载作用情况），作M图，Q图（注意：求跨中弯矩时的正负号规定，同力法一样）讨论：针对位移法中正负号规定判断需要注意的问题。
1、什么是杆端弯矩？例如：如图所示超静定梁假如截AB杆研究，就会暴露出三个内力（弯矩，剪力，轴力），现只研究弯矩，如图所示（夸张放大画出来）：图中所标的即为杆端弯矩，它的作用是相对于杆端而言的。
2、如何判断正负号及运用正负号画弯矩图？M为正的上图中杆端弯矩的方向是假设出来的，由图可知，杆ABM为负的（逆时针）。
