6--两样本Brown-Mood中位数检验

第二十八课 Wilcoxon 秩和检验一、 两样本的Wilcoxon 秩和检验由Mann ，Whitney 和Wilcoxon 三人共同设计的一种检验，有时也称为Wilcoxon 秩和检验，用来决定两个独立样本是否来自相同的或相等的总体。

如果这两个独立样本来自正态分布和具有相同方差时，我们可以采用t 检验比较均值。

但当这两个条件都不能确定时，我们常替换t 检验法为Wilcoxon 秩和检验。

Wilcoxon 秩和检验是基于样本数据秩和。

先将两样本看成是单一样本（混合样本）然后由小到大排列观察值统一编秩。

如果原假设两个独立样本来自相同的总体为真，那么秩将大约均匀分布在两个样本中，即小的、中等的、大的秩值应该大约均匀被分在两个样本中。

如果备选假设两个独立样本来自不相同的总体为真，那么其中一个样本将会有更多的小秩值，这样就会得到一个较小的秩和；另一个样本将会有更多的大秩值，因此就会得到一个较大的秩和。

设两个独立样本为：第一个x 的样本容量为1n ，第二个y 样本容量为2n ，在容量为21n n n +=的混合样本（第一个和第二个）中，x 样本的秩和为x W ，y 样本的秩和为y W ，且有2)1(21+=+++=+n n n W W y x (28.1)我们定义2)1(111+-=n n W W x (28.2)2)1(222+-=n n W W y (28.3)以x 样本为例，若它们在混合样本中享有最小的1n 个秩，于是2)1(11+=n n W x ，也是x W 可能取的最小值；同样y W 可能取的最小值为2)1(22+n n 。

那么，x W 的最大取值等于混合样本的总秩和减去y W 的最小值，即2)1(2)1(22+-+n n n n ；同样，y W 的最大取值等于2)1(2)1(11+-+n n n n 。

所以，(28.2)和(28.3)式中的1W 和2W 均为取值在0与2122112)1(2)1(2)1(n n n n n n n n =+-+-+的变量。

60,88,88,87,60,73,60,97,91,60,83,87,81,90);length( scores)# 输入向量求长度build.price<-c(36,32,31,25,28,36,40,32,41,26,35,35,32,87,33,35 );build.pri cehist(build.price,freq=FALSE)# 直方图lines(density(build.price),col="red")# 连线# 方法一：m<-mean(build.price);m# 均值D<-var(build.price)# 方差SD<-sd(build.price)# 标准差St=(m-37)/(SD/sqrt(length(build.price)));t#t 统计量计算检验统计量t=[1] -0.1412332# 方法二：t.test(build.price-37)# 课本第38 页例2.2binom.test(sum(build.price<37),length(build.price),0.5)# 课本40 页例2.3P<-2*(1-pnorm(1.96,0,1));P[1] 0.04999579P1<-2*(1-pnorm(0.7906,0,1));P1[1] 0.4291774> 例2.4> p<-2*(pnorm(-1.96,0,1));p[1] 0.04999579>> p1<-2*(pnorm(-0.9487,0,1));p1[1] 0.3427732例2.5( P45)scores<- c(95,89,68,90,88,60,81,67,60,60,60,63,60,92,ss<-c(scores-80);sst<-0 t1<-0for(i in 1:length(ss)){if (ss[i]<0) t<-t+1# 求小于80 的个数else t1<-t1+1 求大于80 的个数}t;t1> t;t1[1] 13[1] 15 binom.test(sum(scores<80),length(scores),0.75) p-value = 0.001436<0.01Cox-Staut 趋势存在性检验P47例2.6year<-1971:2002;year length(year)rain<-c(206,223,235,264,229,217,188,204,182,230,223, 227,242,238,207,208,216,233,233,274,234,227,221 ,214, 226,228,235,237,243,240,231,210) length(rain)#(1) 该地区前10 年降雨量是否变化？t1=0for (i in 1:5){if (rain[i]<rain[i+5]) t1<-t1+1}t1k<-0:t1-1sum(dbinom(k,5,0.5))# =0.1875y<-6/(2A5);y# =0.1875P37. 例2.1#(2) 该地区前32 年降雨量是否变化？t=0for (i in 1:16){if (rain[i]<rain[i+16]) t<-t+1}tk1<-0:min(t,16-t)-1sum(dbinom(k1,16,0.5))# =0.0002593994 pbinom(max(k1),16,0.5)#= 0.0002593994y1<-(1 + 16)/(2X6);y1#=0.0002593994plot(year,rain)abline(v=(1971+2002)/2,col=2)lines(year,rain)anova(lm(rain~(year)))随机游程检验( P50)例2.8client<-c("F","M","M","M","M","M","F","M",n1<-sum(client=="M");n1n0<-n-n1;n0 t1<-0 for (i in1:(length(client)-1)){ if (client[i]==client[i+1]) t1<-t1 else t1<-t1+1 }R<-t1+1;R#=12 #find rejection region (不写) 例2.9shuju39<-data.frame(read.table ("SHUJU39.txt",header=TRUE));shuju39attach(shuju39)sum.a=0sum.b=0sum.c=0for (i in 1:length(id)){if (pinzhong[i]=="A") sum.a<-sum.a+chanliang[i] else if (pinzhong[i]=="B") sum.b<-sum.b+chanliang[i]else fuhao<-sum.c<-sum.c+chanliang[i]} sum.a;sum.b;sum.c ma<-sum.a/4 mb<-sum.b/4 mc<-sum.c/4ma;mb;mc fuhao<-rep("a",12);fuhao for (i in1:length(id)){ if (pinzhong[i]=="A" & ((chanliang[i]-ma)>0)) fuhao[i]<-"+"else if (pinzhong[i]=="B" & ((chanliang[i]-mb)>0)) fuhao[i]<-"+"else if (pinzhong[i]=="C" & ((chanliang[i]-mc)>0)) fuhao[i]<-"+"else fuhao[i]<-"-"}fuhao# 利用上题编程解决检验的随机性n<-length(fuhao);nn1<-sum(fuhao=="+");n1 n0<-n-n1;n0t1<-0;clientrl<-1+2*n1*n0/(n1+n0)*(1-1.96/sqrt(n1+n0));rlru<-2*n1*n0/(n1+n0)*(1+1.96/sqrt(n1+n0));ru#=15.33476 (课本为ru=17 )n<-length(client);nfor (i in 1:(length(fuhao)-1)){if (fuhao[i]==fuhao[i+1]) t1<-t1else t1<-t1+1}R<-t1+1;R#find rejection regionrl<-1+2*n1*n0/(n1+n0)*(1-1.96/sqrt(n1+n0));rlru<-2*n1*n0/(n1+n0)*(1+1.96/sqrt(n1+n0));ru 例2.10 ( P52 )library(quadprog)# 不存在叫‘ quadprog '这个名字的程辑包library(zoo)# 不存在叫‘ zoo '这个名字的程辑包library(tseries)# 不存在叫‘ tseries '这个名字的程辑包run1=factor(c(1,1,1,0,rep(1,7),0,1,1,0,0,rep(1,6),0,r ep(1,4), 0,rep(1,5),rep(0,4),rep(1,13))) ；run1y=factor(run1)runs.test(y)# 错误: 没有"runs.test" 这个函数Wilcoxon 符号秩检验W+ 在零假设下的精确分布# 下面的函数dwilxonfun 用来计算W+ 分布密度函数，即P(W+=x) 的一个参考程序！dwilxonfun=function(N){a=c(1,1) #when n=1 frequency of W+=1 or o n=1pp=NULL #distribute of all size from 2 to Naa=NULL #frequency of all size from 2 to N for (i in 2:N){ t=c(rep(0,i),a) a=c(a,rep(0,i))+tp=a/(2A i) #de nsity of Wilcox distribut whe n size=N}p}N=19 #sample size of expected distribution of W+y<-dwilxonfun(N);y #计算P(W+=x) 中的x 取值的R 参考程序！！dwilxonfun=function(N){a=c(1,1) #when n=1 frequency of W+=1 or on=1pp=NULL #distribute of all size from 2 to Naa=NULL #frequency of all size from 2 to Nfor (i in 2:N){t=c(rep(0,i),a)a=c(a,rep(0,i))+tp=a/(2Ai) #density of Wilcox distribut when size=N }a}N=19 #sample size of expected distribution of W+y<-dwilxonfun(N);length(y)-1 hist(y,freq=FALSE) lines(density(y),col="red")例2.12 ( P59)ceo<-c(310,350,370,377,389,400,415,425,440,295, 325,296,250,340,298,365,375,360,385);length(ceo)#方法一wilcox.test(ceo-320)# 方法二ceo.num<-sum(ceo>320);ceo.num n=length(ceo) binom.test(ceo.num,n,0.5)例2.13(P61) a<-c(62,70,74,75,77,80,83,85,88) walsh<-NULLfor (i in 1:(length(a)-1)){for (j in(i+1):length(a)){ walsh<-c(walsh,(a[i]+a[j])/2) } } walsh=c(walsh,a) NW=length(walsh);NW median(walsh)2.5单组数据的位置参数置信区间估计(P61) 例2.14 ‘stu<-c(82,53,70,73,103,71,69,80,54,38,87,91,62,75,65,77);stualpha=0.05 rstu<-sort(stu);rstu conff<-NULL;conff n=length(stu);n for(i in 1:(n-1)){for (j in(i+1):n){ conf=pbinom(j,n,0.5)-pbinom(i,n,0.5) if (conf>1-alpha){conff<-c(conff,i,j,conf)}}}conff length(conff) min<-103-38;minc<-seq(1,(length(conff)-1),3);c for(i in c){col<-c(rstu[conff[i]],rstu[conff[i+1]],conff[i+2]) min1<-rstu[conff[i+1]]-rstu[conff[i]] if(min1<min){min<-min1;l<-i}print(col)}col1<-c(rstu[conff[l]],rstu[conff[l+1]],conff[l+2]);col1 min 例2.14 “stu<-c(82,53,70,73,103,71,69,80,54,38,87,91,62,75,65,77);stualpha=0.05n=length(stu);nconf=pbinom(n,n,0.5)-pbinom(0,n,0.5);conf for(k in 1:n){conf=pbinom(n-k,n,0.5)-pbinom(k,n,0.5) if (conf<1-alpha){loc=k-1;break}}print(loc)(剩余的例题参考程序在课本)3.6正态记分检验例2.18baby1<-c(4,6,9,15,31,33,36,65,77,88) baby=(baby1-34);babybaby.mean=mean(baby);baby.mean例2.18qiuzhi<-function(x){n=length(x)a=rep(2,n)for (i in 1:n){a[i]=sum(x<=x[i])}a}fuhao<-function(x,y){n=length(x)sgn=rep(2,n)for(i in 1:n){if (x[i]>y)sgn[i]=1else if (x[i]==y)sgn[i]=0elsesgn[i]=-1}sgn}n1<-length(baby)babyzhi=qiuzhi(baby) q=(n1+1+babyzhi)/(2*n1+2) babysgn<-fuhao(baby,34)babysgn=sign(baby1-34);babysgn s=qnorm(q,0,1)W<-t(s)%*%babysgn;Wsd<-sum((s*babysg n)A2);sdT=W/sd;T2.7分布的一致性检验例2.19shuju1<-data.frame(month=c(1:6),customers=c(27,18,15,24,36,30));shuju1attach(shuju1)n<-sum(customers);nexpect<-rep(1,6)*(1/6)*n;expectx.squ=sum((customers-expect)A2)/25;x.squ# 方法一value<-qchisq(1-0.05,length(customers)-1);value # 方法pvalue<-1-pchisq(x.squ,length(customers)-1);pvalue例2.20 shuju2<-data.frame(chongshu=c(0:6),zhushu=c(10,24,10,4,1,0,1));shuju2attach(shuju2)n=sum(zhushu);nlamda<-sum(chongshu*zhushu)/n;lamdap<-dpois(chongshu,lamda);p n*px.squ=sum((zhushu A2)/(n *p))-n; x.squ# 方法一value<-qchisq(1-0.05,length(zhushu)-1);value# 方法二pvalue<-1-pchisq(x.squ,length(zhushu)-1);pvalue例2.21 shuju3<-c(36,36,37,38,40,42,43,43,44,45,48,48,50,50,51,52,53,54,54,56,57,57,57,58,58,58,58,58,59,60,61,61,61,62,62,63,63,65,66,68,68,70, 73,73,75);shuju3 n=length(shuju3)n0=sum(shuju3<30);n0n1=sum(shuju3>30 & shuju3<=40);n1n2=sum(shuju3>40 & shuju3<=50);n2n3=sum(shuju3>50 & shuju3<=60);n3n4=sum(shuju3>60 & shuju3<=70);n4n5=sum(shuju3>70 & shuju3<=80);n5 n6=sum(shuju3>80);n6 nn<-c(n0,n1,n2,n3,n4,n5,n6);nn # 计算45 位学生体重分类的频数！shuju3.mean=mean(shuju3);shuju3.meanshuju3.var=var(shuju3);shuju3.var shuju3.sd=sd(shuju3);shuju3.sd e0=pnorm(30,shuju3.mean,shuju3.sd) e1=pnorm(40,shuju3.mean,shuju3.sd)- pnorm(30,shuju3.mean,shuju3.sd) e2=pnorm(50,shuju3.mean,shuju3.sd)- pnorm(40,shuju3.mean,shuju3.sd) e3=pnorm(60,shuju3.mean,shuju3.sd)- pnorm(50,shuju3.mean,shuju3.sd) e4=pnorm(70,shuju3.mean,shuju3.sd)- pnorm(60,shuju3.mean,shuju3.sd) e5=pnorm(80,shuju3.mean,shuju3.sd)- pnorm(70,shuju3.mean,shuju3.sd) e6=1-pnorm(80,shuju3.mean,shuju3.sd) e=c(e0,e1,e2,e3,e4,e5,e6);e ee=n*c(e0,e1,e2,e3,e4,e5,e6);ee x.squ=sum ((nn A 2)/(ee))-n; x.squ # 方法一value<-qchisq(1-0.05,length(ee)-1);value # 方法二pvalue<-1-pchisq(x.squ,length(ee)-1);pvalue例 2.22healthy<-c(87,77,92,68,80,78,84,77,81,80,80,77,92,86,76,80,81,75,77,72,81,90,84,86,80,68,77,87,76,77,7 8,92,75,80,78);healthy#md.xy<-quantile(xy,0.25) # 利用 p 分位数的检 验 t<-sum(xy>md.xy) lx<-length(x) ly<-length(y) lxy<-lx+ly A<-sum(x>md.xy) if (alt=="greater") {w<-1-phyper(A,lx,ly,t)} else if (alt=="less") {w<-phyper(A,lx,ly,t)}conting.table=matrix(c(A,lx-A,lx,t-A,ly-(t-A),ly,t,lxy- t,lxy),3,3)<-c("X","Y","X+Y")<-c(">MXY","<MXY","TOTAL")dimnames(conting.table)<-list(, ) list(contingency.table=conting.table,p.vlue=w)}例 3.2X<-c(698,688,675,656,655,648,640,639,620) Y<-c(780,754,740,712,693,680,621) # 方法一：BM.test(X,Y,"less") # 方法二： XY<-c(X,Y)md.xy<-median(xy) # 利用中位数的检验ks.test(healthy,pnorm,80,6) 第三章 #Brown_Mood 中位数 #Brown-Mood 中位数检验程序 BM.test<-function(x,y,alt){xy<-c(x,y)t<-sum(XY>md.xy) lx<-length(X) ly<-length(Y) lxy<-lx+lyA<-sum(X>md.xy) # 没有修正时的情形 pvalue1<-pnorm(A,lx*t/(lx+ly),sqrt(lx*ly*t*(lx+ly-t)/(lx+lyF3));pvalue1# 修正时的情形pvalue2<-pnorm(A,lx*t/(lx+ly)-0.5,sqrt(lx*ly*t*(lx+ly-t)/(lx+ly)A3));pvalue23.2、Wilcoxon-Mann-Whitney 秩和检验# 求两样本分别的秩和的程序.Qiuzhi<-function(x,y){n1<-length(y)yy<-c(x,y)wm=0for(i in 1:n1){wm=wm+sum(y[i]>yy,1)}wm}例3.3weight.low=c(134,146,104,119,124,161, 107,83,113,129,97,123)m=length(weight.low)weight.high=c(70,118,101,85,112,132,94)n=length(weight.high)# 方法一：wy<-Qiuzhi(weight.low,weight.high)##wy=50 wxy<-wy-n*(n+1)/2;wxy#=22mean<-m*n/2var<-m*n*(m+n+1)/12pvalue<-1-2*pnorm(wxy,mean-0.5,var);pvalue# 方法二wilcox.test(weight.high,weight.low)x1<-c(140,147,153,160,165,170,171,193)x2<-c(130,135,138,144,148,15 5,168)n1<-length(x1)n2<-length(x2)th.hat<-median(x2)-median(x1)B=10000Tboot=c(rep(0,1000))Bootstrapfor (i in 1:B){xx1=sample(x1,5,T)replacement from x1xx2=sample(x2,5,T)replacement from x2Tboot[i]=median(xx2)-median(xx1)}th<-median(Tboot);thse=sd(Tboot)Normal.conf=c(th+qnorm(0.025,0,1)*se,th-qnorm(0.025,0,1)*se);Normal.confPercentile.conf=c(2*th-quantile(Tboot,0.975),2*th- quantile (Tboot,0.025));Percentile.confProvotal.conf=c(quantile(Tboot,0.025),quantile(Tbo ot,0.975));Provotal.confth.hat3.3、Mood 方差检验qiuzhi<-function(x,y){xy<-c(x,y)zhi<-NULLfor (i in 1:length(x)){zhi<-c(zhi,sum(x[i]>=xy))}例3.4Mx-My 的R 参考程序：#vector of length#sample of size n1 with#sample of size n2 with zhi引例：x1<-c(48,56,59,61,84,87,91,95) x2<-c(2,22,49,78,85,89,93,97) zhi_x1=qiuzhi(x1,x2);zhi_x1 #zhi_x2=qiuzhi(x2,x1);zhi_x2 #var_x1=var(x1);var_x1 #var_x2=var(x2);var_x2 m=length(x1);m n=length(x2);nmean_R=(m+n+1)/2;mean_Rmean1=m*(m+n+1)*(m+n-1)/12;mean1var1=m*n*(m+n+1)*(m+n+2)*(m+n-2)/180;var1 M 仁 sum((zhi_x1-mean_R)A2);M1p_value=2*pnorm(M1,mean1-0.5,sqrt(var1)) p_value例 3.5X<-c(4.5,6.5,7,10,12) Y<-c(6,7.2,8,9,9.8) zhi_X=qiuzhi(X,Y);zhi_X m=length(X);m n=length(Y);nmean_R=(m+n+1)/2;mean_Rmean2=m*(m+n+1)*(m+n-1)/12;mean2var2=m*n*(m+n+1)*(m+n+2)*(m+n-2)/180;var2 M2=sum((zhi_X-mean_R)A 2);M2 # 方法一：查附表 9 # 方法二：p_value=2*(1-pnorm(M2,mean2-0.5,sqrt(var2))) p_value # 方法三x14=sum((A[4,]-mean(x1))A2);x14Z=1/(sqrt(var2))*(M2-mean2+0.5);Z3.4 、 Moses 方差检验 qiuzhi<-function(x,y){ xy<-c(x,y) zhi<-NULLfor (i in 1:length(x)){ zhi<-c(zhi,sum(x[i]>=xy)) } zhi}例 3.6x1<-c(8.2,10.7,7.5,14.6,6.3,9.2,11.9, 5.6,12.8,5.2,4.9,13.5) m1=length(x1);m1x2<-c(4.7,6.3,5.2,6.8,5.6,4.2, 6.0,7.4,8.1,6.5) m2=length(x2);m2A<-matrix(x1,ncol=3);A# 随机分组 a1=sample(x1,3,F) xx2=NULL for(i in 1:m1){if(sum(a1==x1[i])==0) xx2=c(xx2,x1[i])}a2=sample(xx2,3,F)xx3=NULL for(i in 1:(m1-3)){if(sum(a2==xx2[i])==0) xx3=c(xx3,x1[i])}a3=sample(xx3,3,F)x11=sum((A[1,]-mean(x1))A2);x11x<-factor(lever);x xy<-data.frame(y,x) attach(xy)aov(formula=y~x,data=xy) aov.xy<-aov(formula=y~x,data=xy) summary(aov.xy)# 方法二： x1<-c(1.4,1.9,2.0,1.5) x2<-c(2.0,2.4,1.8,2.2) x3<-c(2.6,2.8,2.5,2.1) y<-c(x1,x2,x3);yy.mean<-mean(y);y.meanssT<-sum((y-y.mean)A2);ssT # 计算总的平方和 x1.mean<-mean(x1) x2.mean<-mean(x2) x3.mean<-mean(x3)sse<-sum(sum((x1-x1.mean)A2),sum((x2-x2.mean)A2),sum((x3-x3.mean)A2));sse# 计算误差平方和sst<-ssT-sse;sst # 计算组间平方和F<-(sst/2)/(sse/(length(y)-3));F # 计算方差分析的 F 检验统计量 # 临界值的计算value<-qf(0.95,2,length(y)-3);value # 计算 p-value 值p.value<-1-pf(8,2,length(y)-3);p.value表 4.5xueye<-c(8.4,9.4,9.8,12.2, 10.8,15.2,9.8,14.4,8.6,9.8,10.2,9.8, 8.8,9.8,8.9,12.0,8.4,9.2,8.5,9.5);xueye sst1<-sum((xueye-mean(xueye))A2);sst1a=matrix(xueye,ncol=5);aSSA<-c(x11,x12,x13,x14);SSA B<-matrix(x2[1:9],ncol=3);B y1 仁sum((B[1,]-mea n( x2))A 2);y11 y12=sum((B[2,]-mea n( x2))A2);y12 y13=sum((B[3,]-mean(x2))A2);y13 SSB<-c(y11,y12,y13);SSBzhi_SSA=qiuzhi(SSA,SSB);zhi_SSA zhi_SSB=qiuzhi(SSB,SSA);zhi_SSB S=sum(zhi_SSA);S TM=S-4*(4+1)/2;TM # 方法一 (查附表 4)拒绝域 C=(TM<W(0.025,m1,m2) 或者TM>W(0.975,m1,m2))其中 W(0.975,m1,m2)=m1*m2-W(0.025,m1,m2).# 方法二( Wilcoxon 秩和检验) wilcox.test(SSA,SSB) # 方法二( Mann-Whitney 秩和检验) m=length(SSA);m n=length(SSB);nmean_AB=m*n/2;mean_ABvar_AB=m*n*(m+n+1)/12;var_AB p_value=1- pnorm(S,mean_AB,sqrt(var_AB));p_value第四章4.1 、试验设计和方差分析的基本概念回顾 #R 软件中单因素方差分析的函数例 4.1# 方法一：****Analysis of Variance Model **** y<-c(2.0,1.4,2.0,2.8,2.4,1.9,1.8,2.5,2.0,1.5,2.1,2.2);y lever<-c("B","A","C","C","B","A","B","C","A","A","C","B")quzu<-apply(a,2,sum);quzuchuli<-apply(a,1,sum);chuli k=5b=4ssb=1/4*sum(quzuA2)-sum(quzu)A2/(k*b);ssbsst=1/5*sum(chulL2)-sum(chuli)A2/(k*b);sstsse=sst1-ssb-sst;ssemssb=ssb/(k-1);mssbmsst=sst/(b-1);msstmsse=sse/(k*b-k-b+1);msse F1=mssb/msse;F1F2=msst/msse;F2 value1=qf(1-0.05,k-1,k*b-k-b+1) value2=qf(1-0.05,b-1,k*b-k-b+1)例4.3qiuzhi<-function(w,x,y,z){xy<-c(w,x,y,z)zhi<-NULLfor (i in 1:length(w)){zhi<-c(zhi,sum(w[i]>=xy))}zhi}a<-c(80,203,236,252,284,368,457,393)b<-c(133,180,100,160)c<-c(156,295,320,448,465,481,279)d<-c(194,214,272,330,386,475)azhi=qiuzhi(a,b,c,d);azhibzhi=qiuzhi(b,a,c,d);bzhiczhi=qiuzhi(c,a,b,d);czhidzhi=qiuzhi(d,a,b,c);dzhiH=12/( n*(n +1))*(sum(azhi)A2/length(a)+sum(bzhi )A2/le ngth(b) +sum(czhi)A2/length(c)+sum(dzhi)A2/length(d))- (3*(n+1))方法一：value=qchisq(1-0.05,3);value 方法二：pvalue=1-pchisq(H,3);pvaluemean=c(mean(a),mean(b),mean(c),mean(d))# 两两比较的程序bjiao=function(azhi,bzhi,czhi,dzhi){{n=length(c(azhi,bzhi,czhi,dzhi))av=sum(azhi)/length(azhi)bv=sum(bzhi)/length(bzhi)se=sqrt(n*(n+1)/12*(1/length(azhi)+1/length(bzhi) )) d=abs(av-bv) dab=d/sehuizong=c(d,se,dab,qnorm(1-0.05,0,1))} huizong }bjiao(azhi,bzhi,czhi,dzhi) bjiao(czhi,dzhi,azhi,bzhi) 4.3、Jonckheere-Terpstra 检验例4.5x=c(125,136,116,101,105,109)y=c(122,114,131,120,119,127)z=c(128,142,128,134,135,131,140,129)xm=mean(x);xm ym=mean(y);ym zm=mean(z);zmg=c(rep(1,6),rep(2,6),rep(3,8))tapply(c(x,y,z),g,median)JT.test(data=t(c(x,y,z)),class=g) Wij<-function(x,y){zhiij<-0 for(i in 1:n1){zhiij=zhiij+sum(x<y[i])+sum(x==y[i])/2 } zhiij}w12=Wij(x,y);w12 w13=Wij(x,z);w13 w23=Wij(y,z);w23# 方法一：通过查表决策！ # W=sum(w12,w13,w23);W# 方法二：通过中心极限定律决策！ # N=length(c(x,y,z)) n1=length(x) n2=length(y) n3=length(z)E=(N A 2-sum(n"2,n2^2,门3人2))/4丘 #计算 J 的数学期望 #f1=function(n){f=nA2*(2*n+3)}Var=(f1(N)-sum(f1(n1),f1(n2),f1(n3)))/72;Var sd.Var=sqrt(Var);sd.Var # 计算 J 的方差和标 准差# z1=(W-E)/sd.Var;z1 # 可以通过拒绝域来决策 #pvalue=2*(1-pnorm(z,0,1));pvalue # 可以通过 pvalue 值来决策 # 例 4.6jie=function(x,y){{ jiedian<-NULL shuju<-NULL xy<-c(x,y) y1<-unique(y) for (i in 1:length(y1)){n1=length(y) if(sum(xy==y1[i])>1){jiedian<-c(jiedian,sum(xy==y1[i])) shuju<-c(shuju,y1[i]) } }j=c(jiedian,shuju)#shuju 输出是那些数据打结 # }}a=c(40,35,38,43,44,41) b=c(38,40,47,44,40,42) c=c(48,40,45,43,46,44) jie12=jie(a,b);jie12 jie13=jie(a,c);jie13 jie23=jie(b,c);jie23#例 4.7(P128) qiuzhi=function(x){ n1=length(x)n2=length(unique(x)) zhi=NULL if (n1==n2){ for (i in 1:n1){zhi=c(zhi,sum(x<=x[i])) } } else{for (i in 1:n1){zhi=c(zhi,mean(sum(x<x[i],1):sum(x<=x[i]))) } }jiedian=function(x1){n1=length(x1)x2=unique(x1)n2=length(x2)jie=NULLfor(i in 1:n2){n=sum(x1==x2[i])if (n>1) jie=c(jie,n)}jie}a1=c(85,82,82,79)a2=c(87,75,86,82)a3=c(90,81,80,76)a4=c(80,75,81,75)zhi1=qiuzhi(a1);zhi1zhi2=qiuzhi(a2);zhi2zhi3=qiuzhi(a3);zhi3zhi4=qiuzhi(a4);zhi4a1=t(matrix(c(zhi1,zhi2,zhi3,zhi4),ncol=4));a1 b1=apply(a1,2,sum);b1b=4k=4Q=12/(b*k*(k+1))*sum(b"2)-3*b*(k+1);Qjie1=jiedian(a1);jie1jie2=jiedian(a2);jie2jie3=jiedian(a3);jie3jie4=jiedian(a4);jie4jien=c(jie1,jie2,jie3,jie4);jienjie nn=sum(jie n^-jie n);jie nn t1=b*k*(k A2-1);t1Qc=Q/(1-jienn/t1);Qc5.3、Fisher 精确性检验setwd("")getwd()例5.3medicine<-matrix(c(8,2,7,23),,2,byrow=T) medicinefisher.test(medicine)chisq.test(medicine)。

非参数统计(R软件)参考答案本页仅作为文档封面，使用时可以删除This document is for reference only-rar21year.March内容：, ,上机实践：将MASS数据包用命令library(MASS)加载到R中，调用自带“老忠实”喷泉数据集geyer，它有两个变量：等待时间waiting和喷涌时间duration，其中…(1) 将等待时间70min以下的数据挑选出来;(2) 将等待时间70min以下,且等待时间不等于57min的数据挑选出来;(3) 将等待时间70min以下喷泉的喷涌时间挑选出来;(4) 将喷涌时间大于70min喷泉的等待时间挑选出来。

解:读取数据的R命令：library(MASS);#加载MASS包data(geyser);#加载数据集geyserattach(geyser);#将数据集geyser的变量置为内存变量(1) 依题意编定R程序如下：sub1geyser=geyser[which(waiting<70),1];#提取满足条件（waiting<70）的数据,which()，读取下标sub1geyser[1:5];#显示子数据集sub1geyser的前5行[1] 57 60 56 50 54(2) 依题意编定R程序如下：Sub2geyser=geyser[which((waiting<70)&(waiting!=57)),1];#提取满足条件（waiting<70& (waiting!=57)的数据.Sub2geyser[1:5];#显示子数据集sub1geyser的前5行[1] 60 56 50 54 60 ……原数据集的第1列为waiting喷涌时间，所以用[which(waiting<70),2](3)Sub3geyser=geyser[which(waiting<70),2];#提取满足条件（waiting<70）的数据,which()，读取下标Sub3geyser[1:5];#显示子数据集sub1geyser的前5行[1] ……原数据集的第2列为喷涌时间，所以用[which(waiting<70),2](4)Sub4geyser=geyser[which(waiting>70),1];#提取满足条件（waiting<70）的数据,which()，读取下标Sub4geyser[1:5];#显示子数据集sub1geyser的前5行[1] 80 71 80 75 77…….如光盘文件中的数据，一个班有30名学生，每名学生有5门课程的成绩，编写函数实现下述要求：(1) 以的格式保存上述数据；(2) 计算每个学生各科平均分，并将该数据加入(1)数据集的最后一列；(3) 找出各科平均分的最高分所对应的学生和他所修课程的成绩；(4) 找出至少两门课程不及格的学生，输出他们的全部成绩和平均成绩；(5) 比较具有(4)特点学生的各科平均分与其余学生平均分之间是否存在差异。

《非参数统计》教学大纲一、基本信息二、教学目标及任务启发学生，使他们学会用非参数统计方法解决实际问题，对统计应用的广泛性有更进一步的认识。

在学术已掌握的概率论和数理统计的基础上，使学生对统计的基本概念和基本方法在理论上有更深的理解。

三、学时分配教学课时分配四、教学内容及教学要求第一章绪论本章教学目的：使学生对非参数统计方法形成基础的认识，并能够正确区分参数方法与非参数方法，同时掌握非参数统计中的基本概念。

本章主要内容：统计的概念，非参数统计的方法，参数统计与非参数统计的比较。

本章重点、难点：非参数统计方法的概念，参数统计与非参数统计的比较。

本章参考文献：1. 王星编著，非参数统计，中国人民大学出版社，20092. 吴喜之，王兆军编，非参数方法，高等教育出版社，20003. 陈希孺，柴根象编著，非参数统计教程，华东师范大学出版社，19934. 孙山泽编著，非参数统计讲义，北京大学出版社，2000本章思考题：1.请举例说明参数方法与非参数方法之间的区别，并说明它们在什么情况下适用？第一节统计的实践第二节关于非参数统计第三节假设检验及置信区间的回顾第四节渐进相对效率第五节顺序统计量，秩以及正态记分第二章R基础本章教学目的：使学生熟悉并掌握R软件的操作。

本章主要内容：R环境，向量的定义和表示，向量的基本操作，向量的基本运算，向量的逻辑运算，R的图形功能。

本章重点、难点：向量的基本运算与R的图形功能。

本章参考文献：1. 王星编著，非参数统计，中国人民大学出版社，20092. 吴喜之，王兆军编，非参数方法，高等教育出版社，20003. 陈希孺，柴根象编著，非参数统计教程，华东师范大学出版社，19934. 孙山泽编著，非参数统计讲义，北京大学出版社，2000本章思考题：1.在R软件中实现向量的基本运算，并对数据作图。

第一节R环境第二节向量的定义与表示第三节向量的基本操作第四节向量的基本运算第五节向量的逻辑运算第六节R的图形功能第三章单一样本的推断问题本章教学目的：使学生掌握对单一样本的非参数检验方法。

《非参数统计》课程教学大纲课程代码：090531007课程英文名称：Non-parametric Statistics课程总学时：40 讲课：32 实验：8 上机：0适用专业：应用统计学大纲编写（修订）时间：2017.6一、大纲使用说明（一）课程的地位及教学目标《非参数统计》是应用统计学专业的一门专业基础课，是统计学的一个重要分支。

课程主要研究非参数统计的基本概念、基本方法和基本理论。

本课程在教学内容方面除基本知识、基本理论和基本方法的教学外，着重培养学生的统计思想、统计推断和决策能力。

通过本课程的学习，学生将达到以下要求：1．掌握非参数统计方法原理、方法，具有统计分析问题的能力；2．具有根据具体情况正确选用非参数统计方法，正确运用非参数统计方法处理实际数据资料的能力；3．具有运用统计软件分析问题，对计算结果给出合理解释，从而作出科学的定论的能力；4．了解非参数统计的新发展。

（二）知识、能力及技能方面的基本要求1.基本知识：掌握符号检验、Wilcoxon符号秩检验、Cox-Stuart趋势检验、游程检验、Brown-Mood中位数检验、Wilcoxon秩和检验、Kruskal-Wallis检验、Jonckheere-Terpstra检验、Friedman检验、Page检验、Siegel-Tukey检验、Mood检验、Ansari-Bradley检验、Fligner-Killeen检验等非参数统计方法。

2.基本理论和方法：掌握单样本模型、两样本位置模型、多样本数据模型中的位置参数非参数统计检验方法，掌握检验尺度参数是否相等的各种非参数方法，掌握各种回归的方法，掌握分布检验的各种方法，要求能在真实案例中应用相应的方法。

3.基本技能：掌握非参数统计方法的计算机实现。

（三）实施说明1. 本大纲主要依据应用统计学专业2017版教学计划、应用统计学专业建设和特色发展规划和沈阳理工大学编写本科教学大纲的有关规定并根据我校实际情况进行编写。

运用双样本t检验的若干误区与正确条件陈银梦;詹倩【摘要】t检验是假设检验中最常用的检验方法之一,运用较为简单、方便,但生产工作者、科技工作者在初期接触t检验并用之解决问题时,往往因为混淆双样本t检验的适用条件而导致结果不规范.本文总结了在使用双样本t检验时4种典型错误,并附以对应案例.希望能更好地帮助初学者理解双样本t检验的运用及其运用条件,对实验结果做出尽可能精确的分析.【期刊名称】《统计与管理》【年(卷),期】2019(000)002【总页数】3页(P40-42)【关键词】t检验;双样本t检验;独立样本t检验;配对样本t检验;正态分布;方差齐性【作者】陈银梦;詹倩【作者单位】安徽理工大学数学与大数据学院,安徽淮南 232000;安徽理工大学数学与大数据学院,安徽淮南 232000【正文语种】中文【中图分类】N37一、引言在诸多工农业生产、营销活动和科学实验中，一般的数理统计方法，主要是对工作、实验结果进行科学、合理的分析，对某些促销活动、方法、工具、材料或药物等是否有效做出尽可能精确的判断。

如何对实验结果进行综合的科学分析，是生产工作者、科技工作者经常遇到的现实问题。

若分析不当，不仅浪费人力、物力、财力，还将导致实验结果出现偏差，对实验造成难以预计的影响。

T检验是由英国统计学家Gosset为了测定酿酒质量而发现的，他于1908年在Biometrics杂志上以笔名student发表了这篇使他名垂统计史册的论文：《均值的或然误差》，故t检验亦称student t检验（Student's t test）。

后来费希尔给出了此问题的完整证明，并编制了t分布的分位数表，开创了小样本统计推断的新纪元。

t检验主要用于检验独立同分布于N（μ，σ2）的小样本，其中μ、σ均可为未知状态。

生产、科研工作者可以通过使用t分布理论来推论差异发生的概率，从而比较两个样本均值的差异是否显著。

通过T检验可以判别出样本均值的差别不是由抽样误差导致的，同时还可以得到该结果犯第一类错误的概率。

大学生学业成绩情况的实证研究一、引言如今，在丰富多彩的大学校园里，不仅有课堂理论知识，还有各类协会以及学生会社交平台为学生们提供了广阔展示与发展自己才能的空间。

优异的成绩在人们的心中是否还占据着举足轻重的地位，大学生们是否仍把学习放在第一位，一直都是一个有争议的问题。

很多大学生看重综合素质的锻炼与提高，根据自身爱好参加各种活动充实自己，对学习的付出相对少一些；而有些大学生则舍弃其他一切活动，每天致力于学习。

当然，这就涉及到班级干部对班级的管理方式是否合理的问题。

有的班级干部更注重班级的综合管理，认为多方面发展会激发兴趣，灵活大脑，有助于学生对知识的掌握，从而获得优异的学业成绩；有的班级班干部会着重抓好学生们的学习管理，认为只有专心搞学习才能获得优秀的学业成绩。

因此，对于不同的班级管理方式是否会影响学生的学业成绩，有待研究。

学风建设是大学教育教学管理中的重要环节，对学生的学业成绩、顺利毕业和就业等都有至关重要的影响。

宿舍是学生学习和生活的重要场所，宿舍氛围是否对学生学业成绩有显著的影响，也需要实证研究。

此外，在大学校园里，存在着女生的学业成绩要优于男生的学业成绩这一观点，认为女生要比男生更加刻苦，因此成绩也会更加优异，但是，我们也不能忽略男生有更高的智商这一客观条件。

事实是否确实如众所言，引起了笔者探究其究竟的浓厚兴趣。

对于上述三种存在于大学生活中的较为普遍的现象，都有待我们验证研究并得出结论，从而可以证明客观事实的存在，或许也将推翻这些根植于人心的观念。

对于大学生学业成绩情况的研究，国内外有很少学者涉入，尤其国外对其研究的文献几乎为零，国内相关研究也很有限。

例如，对于理论研究，韩月山（2009）分析了非智力因素是造成大学生学业成绩不良的重要人为原因。

对于实证研究，朱省娥，孙熠（2006）运用方差分析、t检验和聚类分析等统计分析方法，揭示出影响学习成绩的因素；张俐，刘波（2009）运用相关分析方法探讨了大学生学业成绩与情绪、个性的关系；祝飞飞（2013）利用SPSS及方差分析，分析了大学生的性别、大学入学成绩、文理科因素与公共基础课程、专业课程及毕业设计环节成绩差异的相关度。

相关样本、独立样本均值分析之比较在实际应用中，我们经常需要比较两个或者多个总体是否有显著差异，比如两个或者多个班级的学习成绩是否有显著差异；针对同一种疾病，两种或多种药物的疗效是否有显著差异；两种或者多种投资的收益是否有显著差异，等等。

实际上这类问题主要还是比较总体之间的平均水平是否存在显著差异。

本文将对这类问题的多种应用场景进行分门别类，帮助大家识别不同的应用场景，进而便于选取对应的正确的分析方法。

分类是人们认识和解决问题最基本的方法之一。

在使用数据分析工具过程中，人们往往需要先界定清楚自己所面临问题的应用场景是怎样的，比如是两样本，还是多样本，是独立样本，还是相关样本，是参数检验还是非参数检验，只有分析清楚了当前的应用场景，才可以选取正确的分析方法。

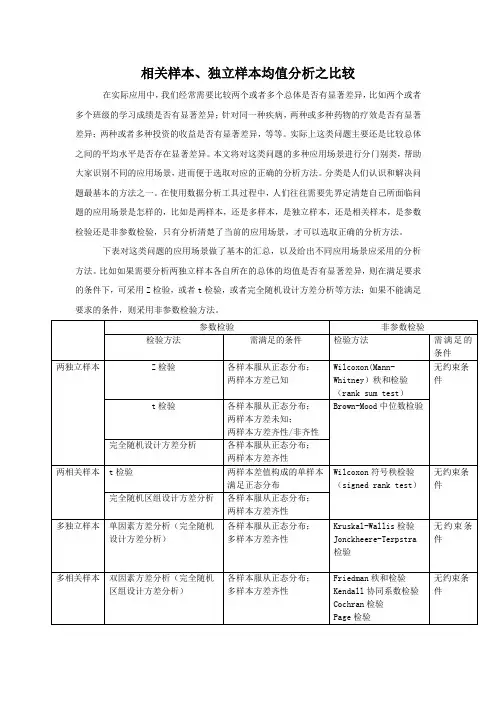
下表对这类问题的应用场景做了基本的汇总，以及给出不同应用场景应采用的分析方法。

比如如果需要分析两独立样本各自所在的总体的均值是否有显著差异，则在满足要求的条件下，可采用Z检验，或者t检验，或者完全随机设计方差分析等方法；如果不能满足要求的条件，则采用非参数检验方法。

说明：1、对于两独立样本的t检验来说，在两样本方差齐性与非齐性两种场景下，t检验统计量与自由度是不同的。

2、Excel工具提供了Z检验方法，而在SPSS工具中，没有提供Z检验的方法，因为t检验方法可以代替Z检验方法。

3、Kruskal-Wallis是双边检验，而Jonckheere-Terpstra是单边检验。

4、Friedman和kendall实际上是同一种检验场景，完全可以使用同一个检验统计量，只是由不同的统计学家给出了两个不同的检验统计量，这两个统计量其实可以互换。

5、与Friedman秩和检验相比，Page检验用于位置参数是否存在趋势的检验，也就是单边检验。

6、Cochran检验：对由二元定性数据构成的完全随机区组设计进行位置参数检验。

《非参数统计》课程设计指导书一、课程设计的目的1. 加深理解本课程的研究方法、思想精髓，提高解决实际问题的能力，熟练掌握Minitab常用统计软件的应用。

2.掌握两样本Brown-Mood中位数检验法，并解决两样本中心位置的一致性检验问题.3.掌握两样本Wilcoxon 秩和检验法，解决两样本中心位置的一致性检验问题。

二、设计名称：不同学科的博士论文除了内容外，页数有没有不同三、设计要求1.数据来源要真实，必须注明数据的出处。

2.尽量使用计算机软件分析，说明算法或过程。

3.必须利用到应用回归分析的统计知识。

4.独立完成，不得有相同或相近的课程设计。

四、设计过程1.思考研究课题，准备搜集数据。

2.确立课题，利用图书馆、上网等方式方法搜集数据。

3.利用机房实验室等学校给予的便利措施开始分析处理数据。

4.根据试验结果，写出课程设计报告书。

5.对实验设计报告书进行完善，并最终定稿。

五、设计细则1.利用的统计学软件主要为Minitab，因为其方便快捷，功能也很强大，界面美观。

2.对Word文档进行编辑的时候，有些特殊的数学符号需要利用数学编辑器这款小软件进行编辑。

3.数据来自较权威机构，增加分析的准确性及可靠性。

4.力求主题突出，观点鲜明，叙述简洁明了。

六、说明1.数据来源于21实际统计学系列教材非参数统计；2.所选取数据可能不会涉及到所学的各种分析方法，本课程设计最后会对此情况作出解释。

3.同一题可以采用不同的方法来检验，从而得出更详细的分析及解释4.05α=.0课程设计任务书课程设计报告课程：非参数统计分析学号：姓名：班级：12金统教师：孙丽玢江苏师范大学数学及统计科学学院设计名称：不同学科的博士论文除了内容外，页数有没有不同日期：2014年 6 月 16 日设计内容：不同学科的博士论文除了内容以外还有什们不同呢？分别对一个大学的数学20个和经济学的18个博士论文的页数进行的抽样结果如下（单位：页数）：数学： 56 105 63 88 72 112 96 93 65 105 94 87 64 65 68 87 90 98 76 75经济学：88 94 93 96 99 79 91 94 91 100 99 90 100 110 102 95 98 85 仅仅从页数上看，这两个学科的博士论文有什么不同？（1）使用两样本Brown-Mood中位数检验法进行分析。

Wilcoxon 秩和检验Wilcoxon 符号秩检验是由威尔科克森（F·Wilcoxon）于1945年提出的。

该方法是在成对观测数据的符号检验基础上发展起来的，比传统的单独用正负号的检验更加有效。

1947年，Mann 和Whitney 对Wilcoxon 秩和检验进行补充，得到Wilcoxon-Mann-Whitney 检验，由后续的Mann-Whitney 检验又继而得到Mann-Whitney-U 检验。

一、 两样本的Wilcoxon 秩和检验由Mann ，Whitney 和Wilcoxon 三人共同设计的一种检验，有时也称为Wilcoxon 秩和检验，用来决定两个独立样本是否来自相同的或相等的总体。

如果这两个独立样本来自正态分布和具有相同方差时，我们可以采用t 检验比较均值。

但当这两个条件都不能确定时，我们常替换t 检验法为Wilcoxon 秩和检验。

Wilcoxon 秩和检验是基于样本数据秩和。

先将两样本看成是单一样本（混合样本）然后由小到大排列观察值统一编秩。

如果原假设两个独立样本来自相同的总体为真，那么秩将大约均匀分布在两个样本中，即小的、中等的、大的秩值应该大约均匀被分在两个样本中。

如果备选假设两个独立样本来自不相同的总体为真，那么其中一个样本将会有更多的小秩值，这样就会得到一个较小的秩和；另一个样本将会有更多的大秩值，因此就会得到一个较大的秩和。

设两个独立样本为：第一个x 的样本容量为1n ，第二个y 样本容量为2n ，在容量为21n n n +=的混合样本（第一个和第二个）中，x 样本的秩和为x W ，y 样本的秩和为y W ，且有2)1(21+=+++=+n n n W W y x (1)我们定义2)1(111+-=n n W W x (2)2)1(222+-=n n W W y (3)以x 样本为例，若它们在混合样本中享有最小的1n 个秩，于是2)1(11+=n n W x ，也是x W 可能取的最小值；同样y W 可能取的最小值为2)1(22+n n 。