利用频率分布直方图计算中位数知识分享

频率分布直方图
用样本的数字特征估计总体的数字特征
1、 众数：在一组数据中，出现次数最多的数称为众数
2、 中位数：在按大小依次排列的一组数据中，当一组数有奇数个时，居于中间的数称为中位数，当一组数据有偶数个是，居于中间两数的平均数称为中位数
3、 平均数：是指一组数据的算术平均数
若是频率分布直方图中，这样计算：
1、 众数：在频率分布直方图中，用面积最大的矩形的横轴中点对应的数来估计众数（最高矩形的横坐标中点）
2、 中位数：在频率分布直方图中，是用使图形左右两边面积相等的与横轴垂直的直线所对应的横坐标来估计中位数。

3、 平均数：在频率分布直方图中，利用每个小矩形的面积乘以小矩形底边中点的横坐标之和来估计平均数。

例题：依据右图频率分布直方图，估计以下
（1） 众数
（2） 中位数
（3） 平均数
例题：某学校100名学生期中考试语文成果的频率分布直方图如图4所示，其中成果分组区间是：[)60,50，[)70,60，[)80,70，[)90,80，[]100,90．
(1) 求图中a 的值
(2) 依据频率分布直方图，估计这100名学生语文成果的平均分；
(3) 若这100名学生语文成果某些分数段的人数()x 与数学成果相应分数段的人数()y 之比如下表所示，求数学成果在[)90,50之外的人数． 分数段
[)60,50 [)70,60 [)80,70 [)90,80 x ：y
1：1 2：1 3：4 4：5
0.005。

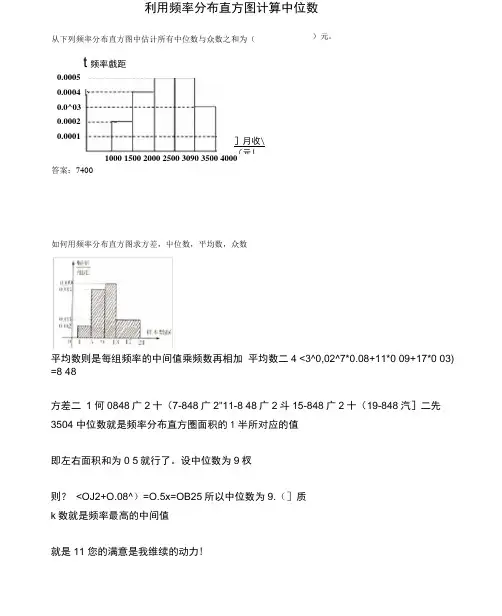
利用频率分布直方图计算中位数从下列频率分布直方图中估计所有中位数与众数之和为（答案：7400如何用频率分布直方图求方差，屮位数，平均数，众数平均数则是每组频率的中间值乘频数再相加 平均数二4 <3^0,02^7*0.08+11*0 09+17*0 03) =8 48方差二 1 何0848广2十（7-848广2"11-8 48广2斗15-848广2十（19-848汽］二先 3504 中位数就是频率分布直方圏面积的1半所对应的值 即左右面积和为0 5就行了。

设中位数为9杈则？ <OJ2+O.08^）=O.5x=OB25所以中位数为9.（］质 k 数就是频率最高的中间值 就是11 您的满意是我维续的动力!）元。

0.0005 t 频率戲距0.0002 0.0001］月收\（元!1000 1500 2000 2500 3090 3500 40000.0004 卜 0.0^03己知一组数据的频率分布直方图如图所示•求众数、中位数、平均数•封仙在换專号布必芳開中,金敷是很•检卜衣芳那諂庭边巧中克極主林的值9 □俭蛙昙血苛卜七方尼的如:刈黑的竹屛蛭「军口业昙笆小萩方葩竝比甲I 点的嵐坐标与对应權牢的舉的和-宙此求岀即h,irffi 单：胸饗军分滞直再13町ML自［Q*atn+6・mO"ILG扁碳而从響零的介界銓& BT护ttffc物册.平场變肖56 « Q. 3*66 *0. 4*?5 «U.】5+盹"0・"肪虫0・占译I *題可用预不和帝頁产89・第看了牢險悔的心皆，中值歎和F垢或•蔚胆劃・簞閉幻应杞毘处帥.申伦鱼塩购釦更*・骨网岸出畠「h•眄如图所示是一样本的频率分布直方图，则由图形屮的数据，可以估计众数与中位数）分别是0.1 0.04jjL ■ ■ ■01 5 10 15 20 数众数是频率分布直方图中最高矩形的底边中点的横坐标，•••中间的一个矩形最高，故10与15的中点是12.5 ,众数是12.5而中位数是把频率分布直方图分成两个面积相等部分的平行于第一个矩形的面积是0・2 ,第三个矩形的面积是0・3 ,故将第二个矩形分成3： 2即可•••中位数是13故选B・为了了解某校1000名初中生右眼视力情况，随机对50名学生右眼视力进行了检查，绘制了如下统计表和频率分布直方图.|视力| 0.1 || 0.2 | 1 0.3 I I 0.4 I| 0.5 || 0.6 || 0.7 || 0.8 ||1人数「II X 1 1 3 || 2|| 3 || 4|| 2 || IA •12.5 12.5B •12.5 13C . 13 12.5 D. 13 13Y轴的直线横坐标请解 答下列问题：（1）补全统计表和频率分布直方图：（2 ）填空：在这个问题中，样本是血•名学牛右眼视力，在这个样本中，视力的中血数是1 ,视力的众 数落在频率分布直方图（从左至右依次是第一、二、三、四丄五小组）的第四小组内；（3 ）如果右眼视力在0.6及0.6以下的必须娇正，试估计该校右眼视力必须娇正的学生约有多少人？组和第三组的频率，接着得到其他小组的频率，然后利用这些已知条件可以求出观力为 。

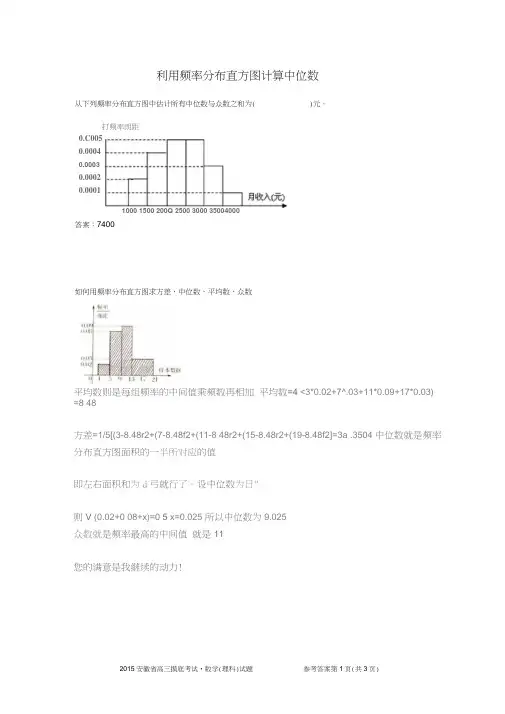
2015安徽省高三摸底考试•数学(理科)试题 参考答案第1页(共3页)利用频率分布直方图计算中位数从下列频率分布直方图中估计所有中位数与众数之和为(答案：7400如何用频率分布直方图求方差，中位数，平均数，众数平均数则是每组频率的中间值乘频数再相加 平均数=4 <3*0.02+7^.03+11*0.09+17*0.03)=8 48方差=1/5[(3-8.48r2+(7-8.48f2+(11-8 48r2+(15-8.48r2+(19-8.48f2]=3a .3504 中位数就是频率分布直方图面积的一半所对应的值即左右面积和为d 弓就行了。

设中位数为日" 则V (0.02+0 08+x)=0 5 x=0.025 所以中位数为9.025 众数就是频率最高的中间值 就是11您的满意是我継续的动力!)元。

打频率朗距0.C005 0.00040.00030.0002 0.00011000 1500 200Q 2500 3000 35004000已知一组数据的频率分布直方图如图所示•求众数、中位数、平均数.傅折匕 在频母廿布直方田中■处敷壬良鬲的丿卜杀方降的麻边的中廉横坐标的虫・中位做是所有小疋方邢的両积昶等的井界战，平均敘乞各小世方飛底边中 点的植圭特与对应频卑的职的和.由此求出即叫. 由m 04=0”鼻 所哄面枳相等的廿邪疑沟EE ，即中位皱为E5； 平均如 55X0. 3+S5 X(J. 4+75 XO. ] 6+65X0. 1+95XD, 05=67.斗題利用頻卑廿冇直方囲，老查了苯致宛的应数“申位敷和平均数抽河題，靜腿吋应根据心蚁.中位我限憑平■均数时意56廿别求出它Tl ・是基财更.如图所示是一样本的频率分布直方图， 则由图形中的数据， 可以估计众数与中位数） 分别是（ ）A • 12.5 12.5B • 12.5 13C . 13 12.5D . 13 13众数是频率分布直方图中最高矩形的底边中点的横坐标， 二中间的一个矩形最高，故10与15的中点是12.5，众数是12.5 而中位数是把频率分布直方图分成两个面积相等部分的平行于Y 轴的直线横坐标第一个矩形的面积是0.2，第三个矩形的面积是0.3，故将第二个矩形分成3 : 2即可 二中位数是13 故选B .为了了解某校1000名初中生右眼视力情况，随机对50名学生右眼视力进行了检查，绘制了如下统计表和频率 分布直方图.视力0.1 0.2 0.3 0.4 0.5 0.6 0.70.8人数1132342解：日频率静布宜方图可知. 歳裁划咚二卫丸亦点评;视力 0.9 1 1.0 1| 1.1 || 1.2 | 1.3 | 1.4 11.5 || | 人数| 2 || 4 || 8 |4 |2 16 II 1请解答下列问题：（1 ）补全统计表和频率分布直方图；（2） 填空：在这个问题中，样本是50名学生右眼视力，在这个样本中，视力的中位数是丄，视力的众数落在频 率分布直方图（从左至右依次是第一、二、三、四、五小组）的第四小组内；（3） 如果右眼视力在0.6及0.6以下的必须矫正，试估计该校右眼视力必须矫正的学生约有多少人？（1） 首先根据喪格可以得到第一组的頻率，然后根据频率分布直芳图可以得到第二小 组和第三粗的频率，接着得到其他小组的频率，然后利用这些已知条件可以求出视力为 D 左的人数，也可収得封视力为1」的人数，也就可以补全统计表和頻率分布直肓图，（2） 根据样本的定义可以确定这个问题中的样本，根据中位数的定义可以确定这组数据的中位魏；（3）根据表格可以得到刃人中有多少人的视力必须矫正，然后利用样本估计总体的思想即可得到该校右眼视力必狈矫正的学生约肓多少人.2-2-5.视力沖11的人敌■生0. 1 0 20.30 40.5 0.6 0.7 0.8 1 1 3 2 3 4 25 0 9 1.0 11 1.2 1.3 1.4 1.5 24 38 42 6（2）在这个间题中，样本是刃名学主右眼视力，在这个样本中，视力的中位数是1』， 视力的金数螯在頻率分布直右图（从左至右依次是第一、二、三、四、五小组）的第四小组内;（3）如果右眼视力在0.6^0.61^下的必、须矫正，那么刘人中育沏人必须矫正,由此可以佶计该校右眼视力边颁矫正的学生釣＜14^50X 1000-280人.此题比较复朵.内容氏较多，主要考查读频数分布直方图的能丈I 和利用统计图获取信息的能力，利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的 判斷和禅决问题.分析 解答.fTi" ■（1）第一组育5人，第二组有9人,点评。

频率分布直方图总结知识点一、频率分布直方图的概念频率分布直方图是用矩形条表示不同数值范围内的频率大小，通常横轴表示变量取值范围，纵轴表示频率大小，每一个矩形条代表一个数值范围内的频数或频率。

通过频率分布直方图可以很直观地了解数据的情况，包括集中趋势、离散程度、分布形态等。

频率分布直方图通常用于展示定量数据的分布情况，对于分布形态的观察和分析有很大帮助。

二、频率分布直方图的绘制方法绘制频率分布直方图，首先需要确定数据的分组方式，然后计算每个组别的频数或频率，最后将这些频数或频率用矩形条表示出来。

具体步骤如下：1、确定数据的分组方式。

根据数据的范围和集中趋势等情况，确定每个组别的宽度和数量，通常选择等宽分组或等频分组。

2、计算每个组别的频数或频率。

根据所选的分组方式，对数据进行分组，然后统计每个组别的数据个数或频率大小。

3、绘制直方图。

将每个组别的频数或频率用矩形条表示出来，横坐标为变量的取值范围，纵坐标为频数或频率的大小，通过矩形条的高度来表示频数或频率的大小。

4、添加标签和标题。

在直方图上添加变量名称、频数或频率大小的标签，以及整个图形的标题，使得图形更加清晰和完整。

通过以上步骤，就可以绘制出频率分布直方图，从而观察和分析数据的分布情况。

三、频率分布直方图的解析内容频率分布直方图提供了丰富的信息，可以从多个方面对数据的情况进行解析，主要包括以下几个方面：1、集中趋势。

通过直方图的形状和位置来判断数据的集中趋势，例如对称分布、偏态分布、峰态分布等，从而了解数据的平均值和中位数等位置指标。

2、离散程度。

通过直方图的分布形态和宽窄程度来判断数据的离散程度，例如集中分布、散布分布等，从而了解数据的标准差和离散系数等离散程度指标。

3、分布形态。

通过直方图的形态和峰度来判断数据的分布形态，例如正态分布、偏态分布等，从而了解数据的分布形状和规律性。

4、异常值检测。

通过直方图来观察是否存在异常值或者极端值，从而对数据的异常情况进行检测和判断。

利用频率分布直方图计算中位数从下列频率分布直方图中估计所有中位数与众数之和为（）元。

答案：7400
如何用频率分布直方图求方差，中位数，平均数，众数
已知一组数据的频率分布直方图如图所示．求众数、中位数、平均数．
如图所示是一样本的频率分布直方图，则由图形中的数据，可以估计众数与中位数）分别是( )
A．12.5 12.5 B．12.5 13 C．13 12.5 D．13 13
众数是频率分布直方图中最高矩形的底边中点的横坐标，
∴中间的一个矩形最高，故10与15的中点是12.5，众数是12.5
而中位数是把频率分布直方图分成两个面积相等部分的平行于Y轴的直线横坐标
第一个矩形的面积是0.2，第三个矩形的面积是0.3，故将第二个矩形分成3：2即可
∴中位数是13
故选B．
为了了解某校1000名初中生右眼视力情况，随机对50名学生右眼视力进行了检查，绘制了如下统计表和频率分布直方图．
视力0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8
人数 1 1 3 2 3 4 2
视力0.9 1.0 1.1 1.2 1.3 1.4 1.5
人数 2 4 8 4 2 6
请解答下列问题：
（1）补全统计表和频率分布直方图；
（2）填空：在这个问题中，样本是50名学生右眼视力，在这个样本中，视力的中位数是1，视力的众数落在频率分布直方图（从左至右依次是第一、二、三、四、五小组）的第四小组内；
（3）如果右眼视力在0.6及0.6以下的必须矫正，试估计该校右眼视力必须矫正的学生约有多少人？。

频数分布表法计算中位数公式
我们要找出频数分布表法计算中位数的公式。

首先，我们需要了解什么是中位数。

中位数是一组数据排序后处于中间位置的数值。

如果数据量是奇数，中位数就是中间那个数；
如果数据量是偶数，中位数就是中间两个数的平均值。

假设我们有一个频数分布表，其中每个数值的频数都已知。

我们可以用以下公式来计算中位数：
1. 找出所有数值的总频数。

2. 如果总频数是奇数，直接找到中间的数值；如果总频数是偶数，找到中间两个数值。

3. 如果找到的数值是频数，则取其代表的数值；如果是两个数值，则取它们的平均值。

计算结果为：中位数是。

所以，使用频数分布表法计算中位数的公式为：
中位数 = (第10个数 + 第11个数) / 2。

【知识要点】一、用样本估计总体的两个手段（用样本的频率分布估计总体的分布；用样本的数字特征估计总体的数字特征），需要从总体中抽取一个质量较高的样本，才能不会产生较大的估计偏差，且样本容量越大，估计的结果也就越精确，分析数据的一种基本方法是用图将它们画出来，或者用紧凑的表格改变数据的排列方式，作图可以达到两个目的，一是从数据中提取信息，二是利用图形传递信息.二、频率分布是指一个样本数据在各个小范围内所占比例的大小.一般是用频率分布直方图反映样本频率分布.三、样本的数字特征众数：就是数据中出现次数最多的那个，比其他的都多，如果几个数据出现的次数都是最多，则它们都是众数；每个数据都只有一次，那么数据没有众数.所以众数可以不止一个或者没有.中位数：就是这些数据排列好了以后中间的那个数字，那么如果有偶数个数据，那么就是中间两个数字的平均数，如果有奇数个数据，则中间那个就是数据的中位数.所以数据的中位数不一定在数据中.平均数：这个就是把所有数据相加，除以个数，就是数据的平均数. nx n++(n x x ++-2)(n x x x n++-四、茎叶图茎叶图又称“枝叶图”，它的思路是将数组中的数按位数进行比较，将数的大小基本不变或变化不大的位作为一个主干（茎），将变化大的位的数作为分枝（叶），列在主干的后面，这样就可以清楚地看到每个主干后面的几个数，每个数具体是多少.当数据是两位有效数字时，用中间的数字表示十位数，即第一个有效数字，两边的数字表示个位数，即第二个有效数字，它的中间部分像植物的茎，两边部分像植物茎上长出的叶子，因此通常把这样的图叫做茎叶图.【方法讲评】【例1】对某小区100户居民的月均用水量进行统计，得到样本的频率分布直方图如图，则估计此样本的众数、中位数分别为（）A. 2.25，2.5 B．2.25，2.02 C．2，2.5 D．2.5，2.25【点评】（1）求频率分布图中的众数，一般先计算出频率分布直方图中的每个小矩形的面积，找到面积最大的那个矩形，取该矩形的横边中点对应的数为众数.（2）求众数也可以直接找最高矩形的横边的中点.【反馈检测1】某学校900名学生在一次百米测试中，成绩全部介于13秒与18秒之间，抽取其中50个样本，将测试结果按如下方式分成五组：第一组[13，14]，第二组[14，15），…，第五组[17，18]，如图是按上述分组方法得到的频率分布直方图．（1）若成绩小于14秒认为优秀，求该样本在这次百米测试中成绩优秀的人数；（2）请估计学校900名学生中，成绩属于第四组的人数；（3）请根据频率分布直方图，求样本数据的众数和中位数．【例2】高二某班50名学生在一次百米测试中，成绩全部都介于13秒到18秒之间，将测试结果按如下方式分成五组，第一组[13，14），第二组[14，15）…第五组[17，18]，如图是按上述分组方法得到的频率分布直方图．（1）若成绩大于等于14秒且小于16秒规定为良好，求该班在这次百米测试中成绩为良好的人数． （2）请根据频率分布直方图，估计样本数据的众数和中位数（精确到0.01）．(3)设n m ,表示该班两个学生的百米测试成绩，已知[)[]18,1714,13, ∈n m ，.6个基本事件组成.【点评】求频率分布直方图中的中位数，一般先计算出每个小矩形的面积，通过解方程找到左边面积为0.5的点P ，点P 对应的数就是中位数.【反馈检测2】某公路段在某一时刻内监测到的车速频率分布直方图如图所示． （Ⅰ）求纵坐标中参数h 的值及第三个小长方形的面积； （Ⅱ）求车速的众数1v ，中位数2v 的估计值；1122n n xx p x p x p 计算.的中点对应的数，n p 代表第n 个矩形的面积【例3】某校从参加考试的学生中抽出60名学生，将其成绩（均为整数）分成六组[40，50），[50，60）．．．[90，100]后画出如下部分频率分布直方图.观察图形的信息，回答下列问题： （Ⅰ）求成绩落在[70，80）上的频率，并补全这个频率分布直方图； (Ⅱ) 估计这次考试的及格率（60分及以上为及格）和平均分；(Ⅲ) 从成绩是70分以上（包括70分）的学生中选两人，求他们在同一分数段的概率.【解析】（Ⅰ）成绩落在[70，80）上的频率是0．3，频率分布直方图如下图．(Ⅲ) 成绩是70分以上（包括70分）的学生人数为（0．03+0．025+0．005）×10×60=36 所以所求的概率为【点评】求频率分布直方图中的平均数，1122n n x x p x p x p 计算.其中nx 代表第n 个矩形的横边的中点对应的数，n p 代表第n 个矩形的面积.【反馈检测3】某校100名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60），[60，70），[70，80），[80，90），[90，100]． （1）求图中a 的值；（2）根据频率分布直方图，估计这100名学生语文成绩的平均分；（3）若这100名学生语文成绩某些分数段的人数（x ）与数学成绩相应分数段的人数（y ）之比如下表所示，求数学成绩在[50，90）之外的人数．高中数学常见题型解法归纳及反馈检测第63讲: 根据频率分布直方图求中位数众数和平均数参考答案【反馈检测1答案】（1）3；（2）288；（3）15.5，15.74.【反馈检测2答案】（1）0.01h =，第三个小长方形的面积为65；（2）1265,62.5v v ==；（3【反馈检测2详细解析】（Ⅰ）∵所有小长形面积之和为1，∴10h +10×3h +10×4h +10×2h =1， 解得h =0.01， ∴第三个小长方形的面积为：10×4h =10×0.04=0.4． （Ⅱ）车速的众数1v =，车速的中位数是两边直方图的面积相等， 于是得：10×0.01+10×0.03+（2v ﹣60）×0.04=0.5，解得2v =62.5．×10×45+0.03×10×55+0.04×10×65+0.02×10×75=62． 【反馈检测3答案】（1）005.0=a ；（2）73；（3）10.【反馈检测3详细解析】（1）依题意得，()104.003.002.0210=+++a ，解得005.0=a（2）这100名学生语文成绩的平均分为：()分7305.0952.0853.0754.06505.055=⨯+⨯+⨯+⨯+⨯ （3）数学成绩在[50，60）的人数为：100×0.05=5数学成绩在[60，70[70，80数学成绩在[80，90所以数学成绩在[50，90）之外的人数为：102540205100=----。

频数表计算中位数中位数是统计学中常用的一个概念，它是指一组数据中处于中间位置的数值。

在实际应用中，我们常常通过频数表来计算中位数。

本文将以频数表计算中位数为主题，介绍中位数的概念、计算方法以及一些实际案例。

一、什么是中位数？中位数是一组数据中的一个数值，它将数据分为两部分，一部分大于中位数，一部分小于中位数。

可以将中位数理解为数据的中心位置，它能够反映数据的集中趋势。

中位数的计算方法依赖于数据的分布情况，对于对称分布的数据，中位数通常等于数据的平均值；对于非对称分布的数据，中位数可能与平均值不同。

二、如何计算中位数？计算中位数的方法有多种，常用的方法是通过频数表来计算。

频数表是一种统计表格，用于统计各个数值出现的频数（即数据中的个数）。

通过频数表，我们可以清晰地了解数据的分布情况，进而计算中位数。

在计算中位数时，我们首先需要将数据按照从小到大的顺序排列。

然后，我们可以通过频数表来确定中位数所在的位置。

如果数据的个数是奇数，中位数就是位于中间位置的数值；如果数据的个数是偶数，中位数就是中间两个数值的平均值。

举个例子来说明。

假设我们有一组数据：1, 2, 3, 4, 5。

我们可以将它们排列成如下的频数表：数值频数1 12 13 14 15 1由于数据的个数是奇数，中位数就是位于中间位置的数值，即3。

再举一个例子。

假设我们有一组数据：1, 2, 3, 4, 5, 6。

我们可以将它们排列成如下的频数表：数值频数1 12 13 14 15 16 1由于数据的个数是偶数，中位数就是中间两个数值的平均值，即(3+4)/2=3.5。

通过以上两个例子，我们可以看出，在使用频数表计算中位数时，我们需要将数据进行排序，并根据数据的个数来确定中位数所在的位置，从而得出准确的中位数。

三、实际应用案例中位数在实际应用中有着广泛的应用。

下面以几个案例来说明中位数的计算方法和应用场景。

案例一：考试成绩假设一所学校有100名学生参加了一次考试，他们的成绩如下所示：70, 75, 80, 85, 90, 95我们可以将这些成绩排列成频数表：数值频数70 175 180 185 190 195 1由于数据的个数是偶数，中位数就是中间两个数值的平均值，即(80+85)/2=82.5。