Brown-Mood中位数检验

第二十八课 Wilcoxon 秩和检验一、 两样本的Wilcoxon 秩和检验由Mann ，Whitney 和Wilcoxon 三人共同设计的一种检验，有时也称为Wilcoxon 秩和检验，用来决定两个独立样本是否来自相同的或相等的总体。

如果这两个独立样本来自正态分布和具有相同方差时，我们可以采用t 检验比较均值。

但当这两个条件都不能确定时，我们常替换t 检验法为Wilcoxon 秩和检验。

Wilcoxon 秩和检验是基于样本数据秩和。

先将两样本看成是单一样本（混合样本）然后由小到大排列观察值统一编秩。

如果原假设两个独立样本来自相同的总体为真，那么秩将大约均匀分布在两个样本中，即小的、中等的、大的秩值应该大约均匀被分在两个样本中。

如果备选假设两个独立样本来自不相同的总体为真，那么其中一个样本将会有更多的小秩值，这样就会得到一个较小的秩和；另一个样本将会有更多的大秩值，因此就会得到一个较大的秩和。

设两个独立样本为：第一个x 的样本容量为1n ，第二个y 样本容量为2n ，在容量为21n n n +=的混合样本（第一个和第二个）中，x 样本的秩和为x W ，y 样本的秩和为y W ，且有2)1(21+=+++=+n n n W W y x (28.1)我们定义2)1(111+-=n n W W x (28.2)2)1(222+-=n n W W y (28.3)以x 样本为例，若它们在混合样本中享有最小的1n 个秩，于是2)1(11+=n n W x ，也是x W 可能取的最小值；同样y W 可能取的最小值为2)1(22+n n 。

那么，x W 的最大取值等于混合样本的总秩和减去y W 的最小值，即2)1(2)1(22+-+n n n n ；同样，y W 的最大取值等于2)1(2)1(11+-+n n n n 。

所以，(28.2)和(28.3)式中的1W 和2W 均为取值在0与2122112)1(2)1(2)1(n n n n n n n n =+-+-+的变量。

60,88,88,87,60,73,60,97,91,60,83,87,81,90);length( scores)# 输入向量求长度build.price<-c(36,32,31,25,28,36,40,32,41,26,35,35,32,87,33,35 );build.pri cehist(build.price,freq=FALSE)# 直方图lines(density(build.price),col="red")# 连线# 方法一：m<-mean(build.price);m# 均值D<-var(build.price)# 方差SD<-sd(build.price)# 标准差St=(m-37)/(SD/sqrt(length(build.price)));t#t 统计量计算检验统计量t=[1] -0.1412332# 方法二：t.test(build.price-37)# 课本第38 页例2.2binom.test(sum(build.price<37),length(build.price),0.5)# 课本40 页例2.3P<-2*(1-pnorm(1.96,0,1));P[1] 0.04999579P1<-2*(1-pnorm(0.7906,0,1));P1[1] 0.4291774> 例2.4> p<-2*(pnorm(-1.96,0,1));p[1] 0.04999579>> p1<-2*(pnorm(-0.9487,0,1));p1[1] 0.3427732例2.5( P45)scores<- c(95,89,68,90,88,60,81,67,60,60,60,63,60,92,ss<-c(scores-80);sst<-0 t1<-0for(i in 1:length(ss)){if (ss[i]<0) t<-t+1# 求小于80 的个数else t1<-t1+1 求大于80 的个数}t;t1> t;t1[1] 13[1] 15 binom.test(sum(scores<80),length(scores),0.75) p-value = 0.001436<0.01Cox-Staut 趋势存在性检验P47例2.6year<-1971:2002;year length(year)rain<-c(206,223,235,264,229,217,188,204,182,230,223, 227,242,238,207,208,216,233,233,274,234,227,221 ,214, 226,228,235,237,243,240,231,210) length(rain)#(1) 该地区前10 年降雨量是否变化？t1=0for (i in 1:5){if (rain[i]<rain[i+5]) t1<-t1+1}t1k<-0:t1-1sum(dbinom(k,5,0.5))# =0.1875y<-6/(2A5);y# =0.1875P37. 例2.1#(2) 该地区前32 年降雨量是否变化？t=0for (i in 1:16){if (rain[i]<rain[i+16]) t<-t+1}tk1<-0:min(t,16-t)-1sum(dbinom(k1,16,0.5))# =0.0002593994 pbinom(max(k1),16,0.5)#= 0.0002593994y1<-(1 + 16)/(2X6);y1#=0.0002593994plot(year,rain)abline(v=(1971+2002)/2,col=2)lines(year,rain)anova(lm(rain~(year)))随机游程检验( P50)例2.8client<-c("F","M","M","M","M","M","F","M",n1<-sum(client=="M");n1n0<-n-n1;n0 t1<-0 for (i in1:(length(client)-1)){ if (client[i]==client[i+1]) t1<-t1 else t1<-t1+1 }R<-t1+1;R#=12 #find rejection region (不写) 例2.9shuju39<-data.frame(read.table ("SHUJU39.txt",header=TRUE));shuju39attach(shuju39)sum.a=0sum.b=0sum.c=0for (i in 1:length(id)){if (pinzhong[i]=="A") sum.a<-sum.a+chanliang[i] else if (pinzhong[i]=="B") sum.b<-sum.b+chanliang[i]else fuhao<-sum.c<-sum.c+chanliang[i]} sum.a;sum.b;sum.c ma<-sum.a/4 mb<-sum.b/4 mc<-sum.c/4ma;mb;mc fuhao<-rep("a",12);fuhao for (i in1:length(id)){ if (pinzhong[i]=="A" & ((chanliang[i]-ma)>0)) fuhao[i]<-"+"else if (pinzhong[i]=="B" & ((chanliang[i]-mb)>0)) fuhao[i]<-"+"else if (pinzhong[i]=="C" & ((chanliang[i]-mc)>0)) fuhao[i]<-"+"else fuhao[i]<-"-"}fuhao# 利用上题编程解决检验的随机性n<-length(fuhao);nn1<-sum(fuhao=="+");n1 n0<-n-n1;n0t1<-0;clientrl<-1+2*n1*n0/(n1+n0)*(1-1.96/sqrt(n1+n0));rlru<-2*n1*n0/(n1+n0)*(1+1.96/sqrt(n1+n0));ru#=15.33476 (课本为ru=17 )n<-length(client);nfor (i in 1:(length(fuhao)-1)){if (fuhao[i]==fuhao[i+1]) t1<-t1else t1<-t1+1}R<-t1+1;R#find rejection regionrl<-1+2*n1*n0/(n1+n0)*(1-1.96/sqrt(n1+n0));rlru<-2*n1*n0/(n1+n0)*(1+1.96/sqrt(n1+n0));ru 例2.10 ( P52 )library(quadprog)# 不存在叫‘ quadprog '这个名字的程辑包library(zoo)# 不存在叫‘ zoo '这个名字的程辑包library(tseries)# 不存在叫‘ tseries '这个名字的程辑包run1=factor(c(1,1,1,0,rep(1,7),0,1,1,0,0,rep(1,6),0,r ep(1,4), 0,rep(1,5),rep(0,4),rep(1,13))) ；run1y=factor(run1)runs.test(y)# 错误: 没有"runs.test" 这个函数Wilcoxon 符号秩检验W+ 在零假设下的精确分布# 下面的函数dwilxonfun 用来计算W+ 分布密度函数，即P(W+=x) 的一个参考程序！dwilxonfun=function(N){a=c(1,1) #when n=1 frequency of W+=1 or o n=1pp=NULL #distribute of all size from 2 to Naa=NULL #frequency of all size from 2 to N for (i in 2:N){ t=c(rep(0,i),a) a=c(a,rep(0,i))+tp=a/(2A i) #de nsity of Wilcox distribut whe n size=N}p}N=19 #sample size of expected distribution of W+y<-dwilxonfun(N);y #计算P(W+=x) 中的x 取值的R 参考程序！！dwilxonfun=function(N){a=c(1,1) #when n=1 frequency of W+=1 or on=1pp=NULL #distribute of all size from 2 to Naa=NULL #frequency of all size from 2 to Nfor (i in 2:N){t=c(rep(0,i),a)a=c(a,rep(0,i))+tp=a/(2Ai) #density of Wilcox distribut when size=N }a}N=19 #sample size of expected distribution of W+y<-dwilxonfun(N);length(y)-1 hist(y,freq=FALSE) lines(density(y),col="red")例2.12 ( P59)ceo<-c(310,350,370,377,389,400,415,425,440,295, 325,296,250,340,298,365,375,360,385);length(ceo)#方法一wilcox.test(ceo-320)# 方法二ceo.num<-sum(ceo>320);ceo.num n=length(ceo) binom.test(ceo.num,n,0.5)例2.13(P61) a<-c(62,70,74,75,77,80,83,85,88) walsh<-NULLfor (i in 1:(length(a)-1)){for (j in(i+1):length(a)){ walsh<-c(walsh,(a[i]+a[j])/2) } } walsh=c(walsh,a) NW=length(walsh);NW median(walsh)2.5单组数据的位置参数置信区间估计(P61) 例2.14 ‘stu<-c(82,53,70,73,103,71,69,80,54,38,87,91,62,75,65,77);stualpha=0.05 rstu<-sort(stu);rstu conff<-NULL;conff n=length(stu);n for(i in 1:(n-1)){for (j in(i+1):n){ conf=pbinom(j,n,0.5)-pbinom(i,n,0.5) if (conf>1-alpha){conff<-c(conff,i,j,conf)}}}conff length(conff) min<-103-38;minc<-seq(1,(length(conff)-1),3);c for(i in c){col<-c(rstu[conff[i]],rstu[conff[i+1]],conff[i+2]) min1<-rstu[conff[i+1]]-rstu[conff[i]] if(min1<min){min<-min1;l<-i}print(col)}col1<-c(rstu[conff[l]],rstu[conff[l+1]],conff[l+2]);col1 min 例2.14 “stu<-c(82,53,70,73,103,71,69,80,54,38,87,91,62,75,65,77);stualpha=0.05n=length(stu);nconf=pbinom(n,n,0.5)-pbinom(0,n,0.5);conf for(k in 1:n){conf=pbinom(n-k,n,0.5)-pbinom(k,n,0.5) if (conf<1-alpha){loc=k-1;break}}print(loc)(剩余的例题参考程序在课本)3.6正态记分检验例2.18baby1<-c(4,6,9,15,31,33,36,65,77,88) baby=(baby1-34);babybaby.mean=mean(baby);baby.mean例2.18qiuzhi<-function(x){n=length(x)a=rep(2,n)for (i in 1:n){a[i]=sum(x<=x[i])}a}fuhao<-function(x,y){n=length(x)sgn=rep(2,n)for(i in 1:n){if (x[i]>y)sgn[i]=1else if (x[i]==y)sgn[i]=0elsesgn[i]=-1}sgn}n1<-length(baby)babyzhi=qiuzhi(baby) q=(n1+1+babyzhi)/(2*n1+2) babysgn<-fuhao(baby,34)babysgn=sign(baby1-34);babysgn s=qnorm(q,0,1)W<-t(s)%*%babysgn;Wsd<-sum((s*babysg n)A2);sdT=W/sd;T2.7分布的一致性检验例2.19shuju1<-data.frame(month=c(1:6),customers=c(27,18,15,24,36,30));shuju1attach(shuju1)n<-sum(customers);nexpect<-rep(1,6)*(1/6)*n;expectx.squ=sum((customers-expect)A2)/25;x.squ# 方法一value<-qchisq(1-0.05,length(customers)-1);value # 方法pvalue<-1-pchisq(x.squ,length(customers)-1);pvalue例2.20 shuju2<-data.frame(chongshu=c(0:6),zhushu=c(10,24,10,4,1,0,1));shuju2attach(shuju2)n=sum(zhushu);nlamda<-sum(chongshu*zhushu)/n;lamdap<-dpois(chongshu,lamda);p n*px.squ=sum((zhushu A2)/(n *p))-n; x.squ# 方法一value<-qchisq(1-0.05,length(zhushu)-1);value# 方法二pvalue<-1-pchisq(x.squ,length(zhushu)-1);pvalue例2.21 shuju3<-c(36,36,37,38,40,42,43,43,44,45,48,48,50,50,51,52,53,54,54,56,57,57,57,58,58,58,58,58,59,60,61,61,61,62,62,63,63,65,66,68,68,70, 73,73,75);shuju3 n=length(shuju3)n0=sum(shuju3<30);n0n1=sum(shuju3>30 & shuju3<=40);n1n2=sum(shuju3>40 & shuju3<=50);n2n3=sum(shuju3>50 & shuju3<=60);n3n4=sum(shuju3>60 & shuju3<=70);n4n5=sum(shuju3>70 & shuju3<=80);n5 n6=sum(shuju3>80);n6 nn<-c(n0,n1,n2,n3,n4,n5,n6);nn # 计算45 位学生体重分类的频数！shuju3.mean=mean(shuju3);shuju3.meanshuju3.var=var(shuju3);shuju3.var shuju3.sd=sd(shuju3);shuju3.sd e0=pnorm(30,shuju3.mean,shuju3.sd) e1=pnorm(40,shuju3.mean,shuju3.sd)- pnorm(30,shuju3.mean,shuju3.sd) e2=pnorm(50,shuju3.mean,shuju3.sd)- pnorm(40,shuju3.mean,shuju3.sd) e3=pnorm(60,shuju3.mean,shuju3.sd)- pnorm(50,shuju3.mean,shuju3.sd) e4=pnorm(70,shuju3.mean,shuju3.sd)- pnorm(60,shuju3.mean,shuju3.sd) e5=pnorm(80,shuju3.mean,shuju3.sd)- pnorm(70,shuju3.mean,shuju3.sd) e6=1-pnorm(80,shuju3.mean,shuju3.sd) e=c(e0,e1,e2,e3,e4,e5,e6);e ee=n*c(e0,e1,e2,e3,e4,e5,e6);ee x.squ=sum ((nn A 2)/(ee))-n; x.squ # 方法一value<-qchisq(1-0.05,length(ee)-1);value # 方法二pvalue<-1-pchisq(x.squ,length(ee)-1);pvalue例 2.22healthy<-c(87,77,92,68,80,78,84,77,81,80,80,77,92,86,76,80,81,75,77,72,81,90,84,86,80,68,77,87,76,77,7 8,92,75,80,78);healthy#md.xy<-quantile(xy,0.25) # 利用 p 分位数的检 验 t<-sum(xy>md.xy) lx<-length(x) ly<-length(y) lxy<-lx+ly A<-sum(x>md.xy) if (alt=="greater") {w<-1-phyper(A,lx,ly,t)} else if (alt=="less") {w<-phyper(A,lx,ly,t)}conting.table=matrix(c(A,lx-A,lx,t-A,ly-(t-A),ly,t,lxy- t,lxy),3,3)<-c("X","Y","X+Y")<-c(">MXY","<MXY","TOTAL")dimnames(conting.table)<-list(, ) list(contingency.table=conting.table,p.vlue=w)}例 3.2X<-c(698,688,675,656,655,648,640,639,620) Y<-c(780,754,740,712,693,680,621) # 方法一：BM.test(X,Y,"less") # 方法二： XY<-c(X,Y)md.xy<-median(xy) # 利用中位数的检验ks.test(healthy,pnorm,80,6) 第三章 #Brown_Mood 中位数 #Brown-Mood 中位数检验程序 BM.test<-function(x,y,alt){xy<-c(x,y)t<-sum(XY>md.xy) lx<-length(X) ly<-length(Y) lxy<-lx+lyA<-sum(X>md.xy) # 没有修正时的情形 pvalue1<-pnorm(A,lx*t/(lx+ly),sqrt(lx*ly*t*(lx+ly-t)/(lx+lyF3));pvalue1# 修正时的情形pvalue2<-pnorm(A,lx*t/(lx+ly)-0.5,sqrt(lx*ly*t*(lx+ly-t)/(lx+ly)A3));pvalue23.2、Wilcoxon-Mann-Whitney 秩和检验# 求两样本分别的秩和的程序.Qiuzhi<-function(x,y){n1<-length(y)yy<-c(x,y)wm=0for(i in 1:n1){wm=wm+sum(y[i]>yy,1)}wm}例3.3weight.low=c(134,146,104,119,124,161, 107,83,113,129,97,123)m=length(weight.low)weight.high=c(70,118,101,85,112,132,94)n=length(weight.high)# 方法一：wy<-Qiuzhi(weight.low,weight.high)##wy=50 wxy<-wy-n*(n+1)/2;wxy#=22mean<-m*n/2var<-m*n*(m+n+1)/12pvalue<-1-2*pnorm(wxy,mean-0.5,var);pvalue# 方法二wilcox.test(weight.high,weight.low)x1<-c(140,147,153,160,165,170,171,193)x2<-c(130,135,138,144,148,15 5,168)n1<-length(x1)n2<-length(x2)th.hat<-median(x2)-median(x1)B=10000Tboot=c(rep(0,1000))Bootstrapfor (i in 1:B){xx1=sample(x1,5,T)replacement from x1xx2=sample(x2,5,T)replacement from x2Tboot[i]=median(xx2)-median(xx1)}th<-median(Tboot);thse=sd(Tboot)Normal.conf=c(th+qnorm(0.025,0,1)*se,th-qnorm(0.025,0,1)*se);Normal.confPercentile.conf=c(2*th-quantile(Tboot,0.975),2*th- quantile (Tboot,0.025));Percentile.confProvotal.conf=c(quantile(Tboot,0.025),quantile(Tbo ot,0.975));Provotal.confth.hat3.3、Mood 方差检验qiuzhi<-function(x,y){xy<-c(x,y)zhi<-NULLfor (i in 1:length(x)){zhi<-c(zhi,sum(x[i]>=xy))}例3.4Mx-My 的R 参考程序：#vector of length#sample of size n1 with#sample of size n2 with zhi引例：x1<-c(48,56,59,61,84,87,91,95) x2<-c(2,22,49,78,85,89,93,97) zhi_x1=qiuzhi(x1,x2);zhi_x1 #zhi_x2=qiuzhi(x2,x1);zhi_x2 #var_x1=var(x1);var_x1 #var_x2=var(x2);var_x2 m=length(x1);m n=length(x2);nmean_R=(m+n+1)/2;mean_Rmean1=m*(m+n+1)*(m+n-1)/12;mean1var1=m*n*(m+n+1)*(m+n+2)*(m+n-2)/180;var1 M 仁 sum((zhi_x1-mean_R)A2);M1p_value=2*pnorm(M1,mean1-0.5,sqrt(var1)) p_value例 3.5X<-c(4.5,6.5,7,10,12) Y<-c(6,7.2,8,9,9.8) zhi_X=qiuzhi(X,Y);zhi_X m=length(X);m n=length(Y);nmean_R=(m+n+1)/2;mean_Rmean2=m*(m+n+1)*(m+n-1)/12;mean2var2=m*n*(m+n+1)*(m+n+2)*(m+n-2)/180;var2 M2=sum((zhi_X-mean_R)A 2);M2 # 方法一：查附表 9 # 方法二：p_value=2*(1-pnorm(M2,mean2-0.5,sqrt(var2))) p_value # 方法三x14=sum((A[4,]-mean(x1))A2);x14Z=1/(sqrt(var2))*(M2-mean2+0.5);Z3.4 、 Moses 方差检验 qiuzhi<-function(x,y){ xy<-c(x,y) zhi<-NULLfor (i in 1:length(x)){ zhi<-c(zhi,sum(x[i]>=xy)) } zhi}例 3.6x1<-c(8.2,10.7,7.5,14.6,6.3,9.2,11.9, 5.6,12.8,5.2,4.9,13.5) m1=length(x1);m1x2<-c(4.7,6.3,5.2,6.8,5.6,4.2, 6.0,7.4,8.1,6.5) m2=length(x2);m2A<-matrix(x1,ncol=3);A# 随机分组 a1=sample(x1,3,F) xx2=NULL for(i in 1:m1){if(sum(a1==x1[i])==0) xx2=c(xx2,x1[i])}a2=sample(xx2,3,F)xx3=NULL for(i in 1:(m1-3)){if(sum(a2==xx2[i])==0) xx3=c(xx3,x1[i])}a3=sample(xx3,3,F)x11=sum((A[1,]-mean(x1))A2);x11x<-factor(lever);x xy<-data.frame(y,x) attach(xy)aov(formula=y~x,data=xy) aov.xy<-aov(formula=y~x,data=xy) summary(aov.xy)# 方法二： x1<-c(1.4,1.9,2.0,1.5) x2<-c(2.0,2.4,1.8,2.2) x3<-c(2.6,2.8,2.5,2.1) y<-c(x1,x2,x3);yy.mean<-mean(y);y.meanssT<-sum((y-y.mean)A2);ssT # 计算总的平方和 x1.mean<-mean(x1) x2.mean<-mean(x2) x3.mean<-mean(x3)sse<-sum(sum((x1-x1.mean)A2),sum((x2-x2.mean)A2),sum((x3-x3.mean)A2));sse# 计算误差平方和sst<-ssT-sse;sst # 计算组间平方和F<-(sst/2)/(sse/(length(y)-3));F # 计算方差分析的 F 检验统计量 # 临界值的计算value<-qf(0.95,2,length(y)-3);value # 计算 p-value 值p.value<-1-pf(8,2,length(y)-3);p.value表 4.5xueye<-c(8.4,9.4,9.8,12.2, 10.8,15.2,9.8,14.4,8.6,9.8,10.2,9.8, 8.8,9.8,8.9,12.0,8.4,9.2,8.5,9.5);xueye sst1<-sum((xueye-mean(xueye))A2);sst1a=matrix(xueye,ncol=5);aSSA<-c(x11,x12,x13,x14);SSA B<-matrix(x2[1:9],ncol=3);B y1 仁sum((B[1,]-mea n( x2))A 2);y11 y12=sum((B[2,]-mea n( x2))A2);y12 y13=sum((B[3,]-mean(x2))A2);y13 SSB<-c(y11,y12,y13);SSBzhi_SSA=qiuzhi(SSA,SSB);zhi_SSA zhi_SSB=qiuzhi(SSB,SSA);zhi_SSB S=sum(zhi_SSA);S TM=S-4*(4+1)/2;TM # 方法一 (查附表 4)拒绝域 C=(TM<W(0.025,m1,m2) 或者TM>W(0.975,m1,m2))其中 W(0.975,m1,m2)=m1*m2-W(0.025,m1,m2).# 方法二( Wilcoxon 秩和检验) wilcox.test(SSA,SSB) # 方法二( Mann-Whitney 秩和检验) m=length(SSA);m n=length(SSB);nmean_AB=m*n/2;mean_ABvar_AB=m*n*(m+n+1)/12;var_AB p_value=1- pnorm(S,mean_AB,sqrt(var_AB));p_value第四章4.1 、试验设计和方差分析的基本概念回顾 #R 软件中单因素方差分析的函数例 4.1# 方法一：****Analysis of Variance Model **** y<-c(2.0,1.4,2.0,2.8,2.4,1.9,1.8,2.5,2.0,1.5,2.1,2.2);y lever<-c("B","A","C","C","B","A","B","C","A","A","C","B")quzu<-apply(a,2,sum);quzuchuli<-apply(a,1,sum);chuli k=5b=4ssb=1/4*sum(quzuA2)-sum(quzu)A2/(k*b);ssbsst=1/5*sum(chulL2)-sum(chuli)A2/(k*b);sstsse=sst1-ssb-sst;ssemssb=ssb/(k-1);mssbmsst=sst/(b-1);msstmsse=sse/(k*b-k-b+1);msse F1=mssb/msse;F1F2=msst/msse;F2 value1=qf(1-0.05,k-1,k*b-k-b+1) value2=qf(1-0.05,b-1,k*b-k-b+1)例4.3qiuzhi<-function(w,x,y,z){xy<-c(w,x,y,z)zhi<-NULLfor (i in 1:length(w)){zhi<-c(zhi,sum(w[i]>=xy))}zhi}a<-c(80,203,236,252,284,368,457,393)b<-c(133,180,100,160)c<-c(156,295,320,448,465,481,279)d<-c(194,214,272,330,386,475)azhi=qiuzhi(a,b,c,d);azhibzhi=qiuzhi(b,a,c,d);bzhiczhi=qiuzhi(c,a,b,d);czhidzhi=qiuzhi(d,a,b,c);dzhiH=12/( n*(n +1))*(sum(azhi)A2/length(a)+sum(bzhi )A2/le ngth(b) +sum(czhi)A2/length(c)+sum(dzhi)A2/length(d))- (3*(n+1))方法一：value=qchisq(1-0.05,3);value 方法二：pvalue=1-pchisq(H,3);pvaluemean=c(mean(a),mean(b),mean(c),mean(d))# 两两比较的程序bjiao=function(azhi,bzhi,czhi,dzhi){{n=length(c(azhi,bzhi,czhi,dzhi))av=sum(azhi)/length(azhi)bv=sum(bzhi)/length(bzhi)se=sqrt(n*(n+1)/12*(1/length(azhi)+1/length(bzhi) )) d=abs(av-bv) dab=d/sehuizong=c(d,se,dab,qnorm(1-0.05,0,1))} huizong }bjiao(azhi,bzhi,czhi,dzhi) bjiao(czhi,dzhi,azhi,bzhi) 4.3、Jonckheere-Terpstra 检验例4.5x=c(125,136,116,101,105,109)y=c(122,114,131,120,119,127)z=c(128,142,128,134,135,131,140,129)xm=mean(x);xm ym=mean(y);ym zm=mean(z);zmg=c(rep(1,6),rep(2,6),rep(3,8))tapply(c(x,y,z),g,median)JT.test(data=t(c(x,y,z)),class=g) Wij<-function(x,y){zhiij<-0 for(i in 1:n1){zhiij=zhiij+sum(x<y[i])+sum(x==y[i])/2 } zhiij}w12=Wij(x,y);w12 w13=Wij(x,z);w13 w23=Wij(y,z);w23# 方法一：通过查表决策！ # W=sum(w12,w13,w23);W# 方法二：通过中心极限定律决策！ # N=length(c(x,y,z)) n1=length(x) n2=length(y) n3=length(z)E=(N A 2-sum(n"2,n2^2,门3人2))/4丘 #计算 J 的数学期望 #f1=function(n){f=nA2*(2*n+3)}Var=(f1(N)-sum(f1(n1),f1(n2),f1(n3)))/72;Var sd.Var=sqrt(Var);sd.Var # 计算 J 的方差和标 准差# z1=(W-E)/sd.Var;z1 # 可以通过拒绝域来决策 #pvalue=2*(1-pnorm(z,0,1));pvalue # 可以通过 pvalue 值来决策 # 例 4.6jie=function(x,y){{ jiedian<-NULL shuju<-NULL xy<-c(x,y) y1<-unique(y) for (i in 1:length(y1)){n1=length(y) if(sum(xy==y1[i])>1){jiedian<-c(jiedian,sum(xy==y1[i])) shuju<-c(shuju,y1[i]) } }j=c(jiedian,shuju)#shuju 输出是那些数据打结 # }}a=c(40,35,38,43,44,41) b=c(38,40,47,44,40,42) c=c(48,40,45,43,46,44) jie12=jie(a,b);jie12 jie13=jie(a,c);jie13 jie23=jie(b,c);jie23#例 4.7(P128) qiuzhi=function(x){ n1=length(x)n2=length(unique(x)) zhi=NULL if (n1==n2){ for (i in 1:n1){zhi=c(zhi,sum(x<=x[i])) } } else{for (i in 1:n1){zhi=c(zhi,mean(sum(x<x[i],1):sum(x<=x[i]))) } }jiedian=function(x1){n1=length(x1)x2=unique(x1)n2=length(x2)jie=NULLfor(i in 1:n2){n=sum(x1==x2[i])if (n>1) jie=c(jie,n)}jie}a1=c(85,82,82,79)a2=c(87,75,86,82)a3=c(90,81,80,76)a4=c(80,75,81,75)zhi1=qiuzhi(a1);zhi1zhi2=qiuzhi(a2);zhi2zhi3=qiuzhi(a3);zhi3zhi4=qiuzhi(a4);zhi4a1=t(matrix(c(zhi1,zhi2,zhi3,zhi4),ncol=4));a1 b1=apply(a1,2,sum);b1b=4k=4Q=12/(b*k*(k+1))*sum(b"2)-3*b*(k+1);Qjie1=jiedian(a1);jie1jie2=jiedian(a2);jie2jie3=jiedian(a3);jie3jie4=jiedian(a4);jie4jien=c(jie1,jie2,jie3,jie4);jienjie nn=sum(jie n^-jie n);jie nn t1=b*k*(k A2-1);t1Qc=Q/(1-jienn/t1);Qc5.3、Fisher 精确性检验setwd("")getwd()例5.3medicine<-matrix(c(8,2,7,23),,2,byrow=T) medicinefisher.test(medicine)chisq.test(medicine)。

中位数检验统计量是一种用于检验中位数是否符合期望值或零假设的方法。

下面是中位数检验统计量的主要步骤：样本数据排序首先，对样本数据进行排序。

排序后，样本数据按照从小到大的顺序排列。

确定中位数在已排序的样本数据中，找到中间位置的数值。

如果样本数据有偶数个，则中位数是中间两个数的平均值。

检查中位数是否符合期望值或零假设期望值或零假设是中位数检验中假设的一个值。

要检查中位数是否符合期望值或零假设，需要比较中位数与期望值或零假设的值。

计算中位数检验统计量中位数检验统计量是用来衡量中位数与期望值或零假设之间的差异大小。

常见的中位数检验统计量有中位数绝对偏差(MAD)和中位数秩次检验(MRRT)。

MAD是每个数据值与中位数的绝对偏差的平均值。

计算公式为：MAD = Σ|xi - median| / n其中，xi表示每个数据值，median表示中位数，n表示样本大小。

MRRT是一种基于秩次的检验统计量。

它是将样本数据按照与中位数的相对大小进行排序，然后计算每个数据值与中间位置的秩次的平均值。

计算公式为：MRRT = Σ(rank - 1.5) / n其中，rank表示每个数据值的秩次，n表示样本大小。

根据样本大小和检验统计量的值，评估是否拒绝零假设根据样本大小和检验统计量的值，可以评估是否拒绝零假设。

通常情况下，如果检验统计量的值大于预期的临界值，则拒绝零假设。

例如，如果样本大小为50，MAD的临界值为1.48，如果计算得到MAD大于1.48，则拒绝零假设。

计算p值以描述结果的可信度p值是用来衡量结果的可信度的一个指标。

它是比较观察到的结果与零假设之间的差异是否显著。

如果p值小于预先设定的显著性水平（如0.05），则可以认为观察到的结果与零假设之间的差异是显著的，从而拒绝零假设。

否则，不能拒绝零假设。

在计算p值时，需要使用到正态分布的概率密度函数或者累积分布函数。

如果检验统计量是MAD或MRRT等连续型变量，则可以使用正态分布的概率密度函数来计算p值；如果检验统计量是二项型变量（如样本的中位数是否大于某个值），则可以使用二项分布的累积分布函数来计算p值。

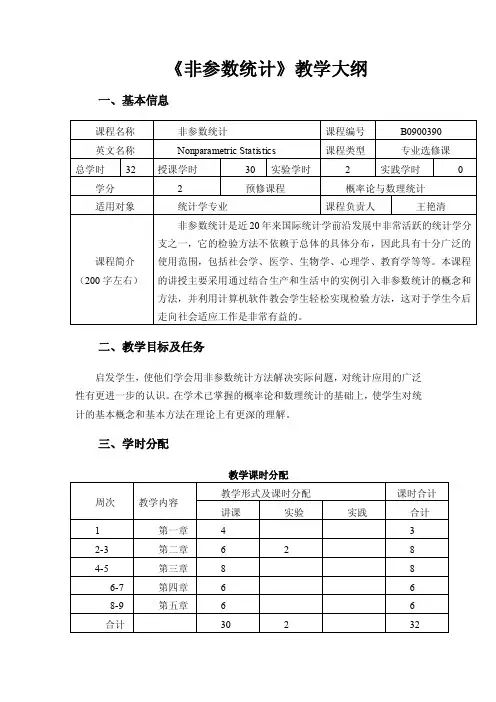
《非参数统计》教学大纲一、基本信息二、教学目标及任务启发学生，使他们学会用非参数统计方法解决实际问题，对统计应用的广泛性有更进一步的认识。

在学术已掌握的概率论和数理统计的基础上，使学生对统计的基本概念和基本方法在理论上有更深的理解。

三、学时分配教学课时分配四、教学内容及教学要求第一章绪论本章教学目的：使学生对非参数统计方法形成基础的认识，并能够正确区分参数方法与非参数方法，同时掌握非参数统计中的基本概念。

本章主要内容：统计的概念，非参数统计的方法，参数统计与非参数统计的比较。

本章重点、难点：非参数统计方法的概念，参数统计与非参数统计的比较。

本章参考文献：1. 王星编著，非参数统计，中国人民大学出版社，20092. 吴喜之，王兆军编，非参数方法，高等教育出版社，20003. 陈希孺，柴根象编著，非参数统计教程，华东师范大学出版社，19934. 孙山泽编著，非参数统计讲义，北京大学出版社，2000本章思考题：1.请举例说明参数方法与非参数方法之间的区别，并说明它们在什么情况下适用？第一节统计的实践第二节关于非参数统计第三节假设检验及置信区间的回顾第四节渐进相对效率第五节顺序统计量，秩以及正态记分第二章R基础本章教学目的：使学生熟悉并掌握R软件的操作。

本章主要内容：R环境，向量的定义和表示，向量的基本操作，向量的基本运算，向量的逻辑运算，R的图形功能。

本章重点、难点：向量的基本运算与R的图形功能。

本章参考文献：1. 王星编著，非参数统计，中国人民大学出版社，20092. 吴喜之，王兆军编，非参数方法，高等教育出版社，20003. 陈希孺，柴根象编著，非参数统计教程，华东师范大学出版社，19934. 孙山泽编著，非参数统计讲义，北京大学出版社，2000本章思考题：1.在R软件中实现向量的基本运算，并对数据作图。

第一节R环境第二节向量的定义与表示第三节向量的基本操作第四节向量的基本运算第五节向量的逻辑运算第六节R的图形功能第三章单一样本的推断问题本章教学目的：使学生掌握对单一样本的非参数检验方法。

《非参数统计》课程教学大纲课程代码：090531007课程英文名称：Non-parametric Statistics课程总学时：40 讲课：32 实验：8 上机：0适用专业：应用统计学大纲编写（修订）时间：2017.6一、大纲使用说明（一）课程的地位及教学目标《非参数统计》是应用统计学专业的一门专业基础课，是统计学的一个重要分支。

课程主要研究非参数统计的基本概念、基本方法和基本理论。

本课程在教学内容方面除基本知识、基本理论和基本方法的教学外，着重培养学生的统计思想、统计推断和决策能力。

通过本课程的学习，学生将达到以下要求：1．掌握非参数统计方法原理、方法，具有统计分析问题的能力；2．具有根据具体情况正确选用非参数统计方法，正确运用非参数统计方法处理实际数据资料的能力；3．具有运用统计软件分析问题，对计算结果给出合理解释，从而作出科学的定论的能力；4．了解非参数统计的新发展。

（二）知识、能力及技能方面的基本要求1.基本知识：掌握符号检验、Wilcoxon符号秩检验、Cox-Stuart趋势检验、游程检验、Brown-Mood中位数检验、Wilcoxon秩和检验、Kruskal-Wallis检验、Jonckheere-Terpstra检验、Friedman检验、Page检验、Siegel-Tukey检验、Mood检验、Ansari-Bradley检验、Fligner-Killeen检验等非参数统计方法。

2.基本理论和方法：掌握单样本模型、两样本位置模型、多样本数据模型中的位置参数非参数统计检验方法，掌握检验尺度参数是否相等的各种非参数方法，掌握各种回归的方法，掌握分布检验的各种方法，要求能在真实案例中应用相应的方法。

3.基本技能：掌握非参数统计方法的计算机实现。

（三）实施说明1. 本大纲主要依据应用统计学专业2017版教学计划、应用统计学专业建设和特色发展规划和沈阳理工大学编写本科教学大纲的有关规定并根据我校实际情况进行编写。

运用双样本t检验的若干误区与正确条件陈银梦;詹倩【摘要】t检验是假设检验中最常用的检验方法之一,运用较为简单、方便,但生产工作者、科技工作者在初期接触t检验并用之解决问题时,往往因为混淆双样本t检验的适用条件而导致结果不规范.本文总结了在使用双样本t检验时4种典型错误,并附以对应案例.希望能更好地帮助初学者理解双样本t检验的运用及其运用条件,对实验结果做出尽可能精确的分析.【期刊名称】《统计与管理》【年(卷),期】2019(000)002【总页数】3页(P40-42)【关键词】t检验;双样本t检验;独立样本t检验;配对样本t检验;正态分布;方差齐性【作者】陈银梦;詹倩【作者单位】安徽理工大学数学与大数据学院,安徽淮南 232000;安徽理工大学数学与大数据学院,安徽淮南 232000【正文语种】中文【中图分类】N37一、引言在诸多工农业生产、营销活动和科学实验中，一般的数理统计方法，主要是对工作、实验结果进行科学、合理的分析，对某些促销活动、方法、工具、材料或药物等是否有效做出尽可能精确的判断。

如何对实验结果进行综合的科学分析，是生产工作者、科技工作者经常遇到的现实问题。

若分析不当，不仅浪费人力、物力、财力，还将导致实验结果出现偏差，对实验造成难以预计的影响。

T检验是由英国统计学家Gosset为了测定酿酒质量而发现的，他于1908年在Biometrics杂志上以笔名student发表了这篇使他名垂统计史册的论文：《均值的或然误差》，故t检验亦称student t检验（Student's t test）。

后来费希尔给出了此问题的完整证明，并编制了t分布的分位数表，开创了小样本统计推断的新纪元。

t检验主要用于检验独立同分布于N（μ，σ2）的小样本，其中μ、σ均可为未知状态。

生产、科研工作者可以通过使用t分布理论来推论差异发生的概率，从而比较两个样本均值的差异是否显著。

通过T检验可以判别出样本均值的差别不是由抽样误差导致的，同时还可以得到该结果犯第一类错误的概率。

方差不齐用什么检验方法方差不齐是指不同样本的方差不相等。

在统计学中，我们常常需要对样本数据进行方差分析，以确定不同组别之间的差异是否显著。

然而，当样本数据的方差不齐时，传统的方差分析方法就不再适用。

那么，面对方差不齐的情况，我们应该采用什么样的检验方法呢？一般来说，当我们进行方差分析时，可以通过Levene检验或者Bartlett检验来检验样本数据的方差是否齐性。

Levene检验是一种非参数检验方法，它不依赖于数据的分布形式，对数据的偏态和峰度不敏感，因此在实际应用中被广泛采用。

Bartlett检验则是一种基于正态分布假设的检验方法，对数据的正态性要求较高。

当然，还有其他一些检验方法，如Brown-Forsythe检验、Fligner-Killeen检验等，它们也可以用来检验方差的齐性。

除了检验方差的齐性外，我们还可以采用一些对方差不齐具有鲁棒性的方法进行方差分析。

比如，Welch's ANOVA方法，它是一种对方差不齐具有鲁棒性的分析方法，可以有效应对方差不齐的情况。

此外，还有Kruskal-Wallis检验、Mood's 中位数检验等非参数方法，它们也可以在方差不齐的情况下进行分析。

总的来说，当我们面对方差不齐的情况时，可以采用Levene检验或者Bartlett 检验来检验方差的齐性，然后选择合适的分析方法进行方差分析。

如果方差不齐且无法满足正态分布假设，可以考虑使用非参数方法进行分析。

在选择检验方法和分析方法时，需要根据具体的数据情况和研究目的来进行合理的选择，以确保分析结果的有效性和可靠性。

综上所述，面对方差不齐的情况，我们可以通过Levene检验、Bartlett检验等方法来检验方差的齐性，然后选择合适的分析方法进行方差分析，也可以考虑使用对方差不齐具有鲁棒性的非参数方法进行分析。

选择合适的方法进行分析，可以有效应对方差不齐带来的问题，确保统计分析的准确性和可靠性。

Wilcoxon 秩和检验Wilcoxon 符号秩检验是由威尔科克森（F·Wilcoxon）于1945年提出的。

该方法是在成对观测数据的符号检验基础上发展起来的，比传统的单独用正负号的检验更加有效。

1947年，Mann 和Whitney 对Wilcoxon 秩和检验进行补充，得到Wilcoxon-Mann-Whitney 检验，由后续的Mann-Whitney 检验又继而得到Mann-Whitney-U 检验。

一、 两样本的Wilcoxon 秩和检验由Mann ，Whitney 和Wilcoxon 三人共同设计的一种检验，有时也称为Wilcoxon 秩和检验，用来决定两个独立样本是否来自相同的或相等的总体。

如果这两个独立样本来自正态分布和具有相同方差时，我们可以采用t 检验比较均值。

但当这两个条件都不能确定时，我们常替换t 检验法为Wilcoxon 秩和检验。

Wilcoxon 秩和检验是基于样本数据秩和。

先将两样本看成是单一样本（混合样本）然后由小到大排列观察值统一编秩。

如果原假设两个独立样本来自相同的总体为真，那么秩将大约均匀分布在两个样本中，即小的、中等的、大的秩值应该大约均匀被分在两个样本中。

如果备选假设两个独立样本来自不相同的总体为真，那么其中一个样本将会有更多的小秩值，这样就会得到一个较小的秩和；另一个样本将会有更多的大秩值，因此就会得到一个较大的秩和。

设两个独立样本为：第一个x 的样本容量为1n ，第二个y 样本容量为2n ，在容量为21n n n +=的混合样本（第一个和第二个）中，x 样本的秩和为x W ，y 样本的秩和为y W ，且有2)1(21+=+++=+n n n W W y x (1)我们定义2)1(111+-=n n W W x (2)2)1(222+-=n n W W y (3)以x 样本为例，若它们在混合样本中享有最小的1n 个秩，于是2)1(11+=n n W x ，也是x W 可能取的最小值；同样y W 可能取的最小值为2)1(22+n n 。

非参数统计》课程教学大纲课程编号：06542 制定单位：统计学院制定人（执笔人）：潘文荣审核人：徐海云制定（或修订）时间：2014年2月28日江西财经大学教务处《非参数统计》课程教学大纲、课程总述、教学时数分配三、单元教学目的、教学重难点和内容设置第一章绪论教学目的】理解非参数统计学习目的和内容。

重点难点】学习非参数统计学的应用意义，明确非参数统计的优缺点。

教学内容】第一节测量的层次第二节假设测验的回顾第三节非参数统计方法第二章单个样本的非参数检验【教学目的】了解符号检验、Wilcoxon 检验、正态计分检验、Cox-Start 趋势检验、游程经验的原理和计算方法，并进行上机操作。

【重点难点】符号检验、游程检验、Wilcoxon 检验的原理和计算方法。

【教学内容】第一节符号检验第二节Wilcoxon 检验第三节正态计分检验第四节Cox-Start 趋势检验第五节游程经验第三章两个相关样本的非参数检验【教学目的】了解符号检验、Wilcoxon 检验在两个相关中的检验，并进行上机操作。

【重点难点】在上一章学习的知识进一步应用到相关处理的比较上。

【教学内容】第一节符号检验第二节Wilcoxon 符号秩检验第四章两个独立样本的非参数检验【教学目的】了解Brown-mood 中位数检验的原理及计算方法，并进行上机操作。

【重点难点】秩和检验的原理和方法【教学内容】第一节Brown-mood 中位数检验第二节秩和检验第五章多个相关样本的非参数检验【教学目的】了解Cochran检验、Friedman检验的原理及计算方法，并进行上机操作。

【重点难点】Fiedman 检验的原理和方法【教学内容】第一节Cochran 检验第二节Friedman 检验第六章多个独立样本的非参数检验【教学目的】了解Kruskal-Wallis 检验、正态计分检验的原理及计算方法，并进行上机操作。

【重点难点】独立样本比较的非参数统计方法。

第二十八课 Wilcoxon 秩和检验一、 两样本的Wilcoxon 秩和检验由Mann ，Whitney 和Wilcoxon 三人共同设计的一种检验，有时也称为Wilcoxon 秩和检验，用来决定两个独立样本是否来自相同的或相等的总体。

如果这两个独立样本来自正态分布和具有相同方差时，我们可以采用t 检验比较均值。

但当这两个条件都不能确定时，我们常替换t 检验法为Wilcoxon 秩和检验。

Wilcoxon 秩和检验是基于样本数据秩和。

先将两样本看成是单一样本（混合样本）然后由小到大排列观察值统一编秩。

如果原假设两个独立样本来自相同的总体为真，那么秩将大约均匀分布在两个样本中，即小的、中等的、大的秩值应该大约均匀被分在两个样本中。

如果备选假设两个独立样本来自不相同的总体为真，那么其中一个样本将会有更多的小秩值，这样就会得到一个较小的秩和；另一个样本将会有更多的大秩值，因此就会得到一个较大的秩和。

设两个独立样本为：第一个x 的样本容量为1n ，第二个y 样本容量为2n ，在容量为21n n n +=的混合样本（第一个和第二个）中，x 样本的秩和为x W ，y 样本的秩和为y W ，且有2)1(21+=+++=+n n n W W y x (28.1)我们定义2)1(111+-=n n W W x (28.2)2)1(222+-=n n W W y (28.3)以x 样本为例，若它们在混合样本中享有最小的1n 个秩，于是2)1(11+=n n W x ，也是x W 可能取的最小值；同样y W 可能取的最小值为2)1(22+n n 。

那么，x W 的最大取值等于混合样本的总秩和减去y W 的最小值，即2)1(2)1(22+-+n n n n ；同样，y W 的最大取值等于2)1(2)1(11+-+n n n n 。

所以，(28.2)和(28.3)式中的1W 和2W 均为取值在0与2122112)1(2)1(2)1(n n n n n n n n =+-+-+的变量。