画法几何 第七章 基本立体

立体图形怎么画立体图形是由三维空间中的几何体构成的，具有长度、宽度和高度三个方向。

常见的立体图形有立方体、长方体、球体、圆锥体、圆柱体等。

在绘制立体图形时，需要遵循一定的规律和技巧，以获得更加真实、精确和美观的效果。

下面将介绍如何绘制常见的立体图形，并提供相关的绘图技巧和实例。

1.立方体的绘制立方体是一种六面体，每个面都是一个正方形。

在绘制立方体时，需要先画定位线，然后绘制正方形的平面，再将他们合成一个六面体。

（1）先画出一个正方形，作为立方体的底面，在底面四个顶点处描绘四个边向上的垂直线，这些线应高出底面边的长度，相交处即为顶部的四个点。

（2）连接底面和顶部，从每个底面上端平行线向上连接，然后向下连接到相应的垂直线，再连接相邻的线段，即得到了一个完整的立方体。

绘制立方体时需要注意以下几点：（1）定位线和平面的尺寸应该相同，以确保立方体的比例正确。

（2）在制作六个正方形时，要保证它们的边缘互相平行，这有助于提高图形的准确性。

（3）在绘制各个面时，应遵循透视原理，即远离我们的面会缩小，而靠近我们的面会增大。

2.长方体的绘制长方体是一种六面体，由两个平行的长方形作为顶部和底部，以及四个矩形作为侧面组成。

与立方体类似，绘制长方体时也需要先绘制定位线和平面。

（1）确定长方体的长度、宽度和高度，以此在画面上虚构出一个长方体的框架。

（2）在底面四个顶点处描绘四个边向上的垂直线，这些线应高出底面边的长度，相交处即为顶部的四个点。

（3）连接底面和顶部，从每个底面上端平行线向上连接，然后向下连接到相应的垂直线，再连接相邻的线段，即得到了一个完整的长方体。

绘制长方体时需要注意以下几点：（1）与立方体相同，定位线和平面的尺寸应该相同，以确保长方体的比例正确。

（2）在制作顶部和底部的两个长方形时，要确保它们的边缘互相平行，这有助于提高图形的准确性。

（3）在绘制矩形时，应遵循透视原理，以确保各个侧面的比例正确。

3.球体的绘制球体是一种三维圆形体，由无数平行的圆形组成，可以绘制出不同的大小和形状。

相贯线是两立体表面的共有线，是由一系列共有点组成的。

透视图中的消失现象：人们在观看周围的景物是的近大远小，并且最终消失于一点的现象。

直线的灭点：某条直线的灭点，即是与该直线平行的视线与画面的交点。

真高线：当前垂线位在画面上，其透视为线段本身，反映真实高度，我们把这种位在画面上的铅垂线的透视为真高线。

至现在透视图中消失的规律是空间相互平行的直线，其透视必然消失于一个共同的灭点。

建筑师法：画透视图最基本的也是最常用的画法，就是运用直线在透视图中的消失特性，求出直线的灭点，再用视线迹点法求出物体上某些点的透视，从而作出物体的透视图。

平面立体的表面展开：平面立体的表面都是多边形，因此画平面立体的表面展开图，就是依次画出各多边形的实形。

图纸的幅面是指图纸本身的大小规格。

图幅为A3的幅面尺寸是297mm*420mm字体：字体工整、笔画清楚、间隔均匀、排列整齐。

尺寸标注包括尺寸界线、尺寸线、尺寸起止符号和尺寸数字及尺寸单位等内容。

基本视图：物体在基本投影面上的投影称为基本视图。

镜像投影：假想在平行于物体的某个表面，设置一个镜面，镜面中则呈现出该物体的像。

按照镜中的像用正投影法来绘制图样，这种方法称为镜像投影法。

剖视图：用假想平面剖切物体，将处在观察者和剖切面之间的部分移去，而将其余部分向投影面投射所得到的图形称为剖视图。

断面图：假想用剖切面将物体的某处切断，仅画出该剖切面与物体接触部分的图形，称为断面图。

钢筋混凝土结构主要是通过立面图，断面图和钢筋详图等，表达构件的形状、大小及钢筋配置情况。

房屋施工图分为：建筑施工图、结构施工图、设备施工图。

建筑施工图主要包括的图样有：建筑总平面图、建筑平面图、建筑立面图、建筑剖面图、建筑详图。

结构施工图主要包括结构设计说明，基础图、结构布置图、构件详图、节点构造详图及预埋件图等。

结构布置图的作用是表示每层的梁、板、柱、墙承重构件的平面布置。

组合体尺寸分为定形尺寸（确定各基本体形状和大小的尺寸.）、定位尺寸（确定各基本体之间相对位置的尺寸.）和总体尺寸（总体尺寸是指组合体的总长度、总宽度和总高度的尺寸）。

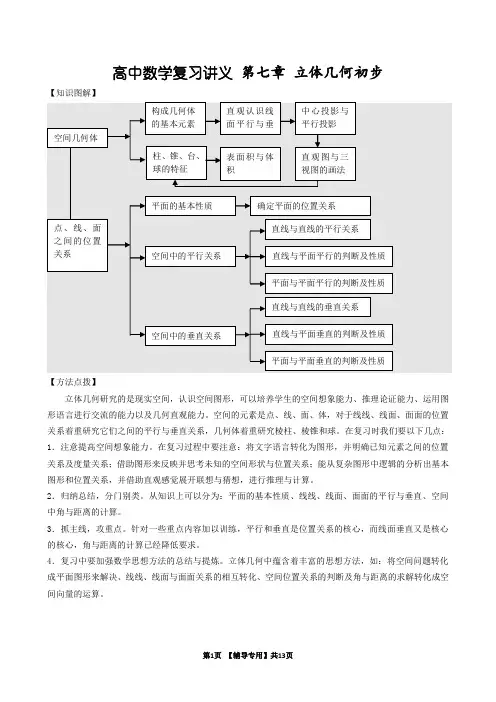
2013高中数学精讲精练第七章立体几何初步2013高中数学精讲精练第七章立体几何初步【知识图解】【方法点拨】立体几何研究的是现实空间，认识空间图形，可以培养学生的空间想象能力、推理论证能力、运用图形语言进行交流的能力以及几何直观能力。

空间的元素是点、线、面、体，对于线线、线面、面面的位置关系着重研究它们之间的平行与垂直关系，几何体着重研究棱柱、棱锥和球。

在复习时我们要以下几点：1．注意提高空间想象能力。

在复习过程中要注意：将文字语言转化为图形，并明确已知元素之间的位置关系及度量关系；借助图形来反映并思考未知的空间形状与位置关系；能从复杂图形中逻辑的分析出基本图形和位置关系，并借助直观感觉展开联想与猜想，进行推理与计算。

2．归纳总结，分门别类。

从知识上可以分为：平面的基本性质、线线、线面、面面的平行与垂直、空间中角与距离的计算。

3．抓主线，攻重点。

针对一些重点内容加以训练，平行和垂直是位置关系的核心，而线面垂直又是核心的核心，角与距离的计算已经降低要求。

4．复习中要加强数学思想方法的总结与提炼。

立体几何中蕴含着丰富的思想方法，如：将空间问题转化成平面图形来解决、线线、线面与面面关系的相互转化、空间位置关系的判断及角与距离的求解转化成空间向量的运算。

第1课 空间几何体【考点导读】1．观察认识柱、锥、台、球及其简单组合体的结构特征，并能运用这些特征描述现实生活中简单物体的结构；2．能画出简单空间图形（长方体、球、圆柱、圆锥、棱柱等的简易组合）的三视图，能识别上述的三视图所表示的立体模型，会用斜二侧法画出它们的直观图；3．通过观察用两种方法（平行投影与中心投影）画出的视图与直观图，了解空间图形的不同表示形式；4.了解球、棱柱、棱锥、台的表面积和体积的计算公式。

【基础练习】1．一个凸多面体有8个顶点，①如果它是棱锥，那么它有 14 条棱， 8 个面；②如果它是棱柱，那么它有 12 条棱 6 个面。

2.（1）如图，在正四面体A －BCD 中，E 、F 、G 分别是三角形ADC 、ABD 、BCD 的中心，则△EFG 在该正四面体各个面上的射影所有可能的序号是 ③④ 。