画法几何 (2.7)平面、直线与立体相交

立体几何中的相交线与平面关系与平面相交是立体几何中常见的问题，相交线与平面的关系在空间几何中具有重要的意义。

本文将介绍相交线与平面的几种常见关系，并探讨其相关性质。

一、线与平面的相交关系1. 直线与平面相交当一条直线与平面相交时，可能会存在以下几种情况：（1）相交于一点：直线与平面相交于一个点时，该点既在直线上，又在平面上。

这种情况下，直线与平面共点，详细表示为：直线l⊂平面P，记作l∩P=P'。

（2）相交于一条直线：直线与平面相交于一条线段时，该线段既在直线上，又在平面上。

这种情况下，直线与平面共线，详细表示为：直线l⊂平面P，记作l∩P=l'。

（3）不相交：直线与平面没有任何公共点，即直线不在平面上，这种情况下，直线与平面没有交点，详细表示为：直线l∩平面P=∅。

2. 曲线与平面相交曲线与平面相交的情况相对复杂，常见情况有以下几种：（1）相交于一个形状：曲线与平面相交于一个封闭曲线或开放曲线时，该曲线既在平面上，又在曲线上。

这种情况下，曲线与平面共形状，详细表示为：曲线C⊂平面P，记作C∩P=C'。

（2）相交于多个点：曲线与平面相交于多个点时，曲线上的每个点都在平面上。

这种情况下，曲线与平面相交于多个点，详细表示为：曲线C∩平面P={P1,P2,P3,…}。

（3）不相交：曲线与平面没有任何公共点，即曲线不在平面上，这种情况下，曲线与平面没有交点，详细表示为：曲线C∩平面P=∅。

二、线与面的相关性质1. 交线垂直于平面的性质当直线与平面相交于一点时，该直线与平面的交线垂直于平面。

这是因为平面上的任意一条垂直于交线的直线都与给定的直线重合于交点，从而证明了两个垂直关系。

2. 平行关系与相交线夹角的性质平行关系是指两条直线在平面上无交点的关系，当两条平行线都与同一平面相交时，它们在该平面上的相交线之间的夹角相等。

这一性质被称为"同位角相等定理"，在立体几何的问题中起到了重要的作用。

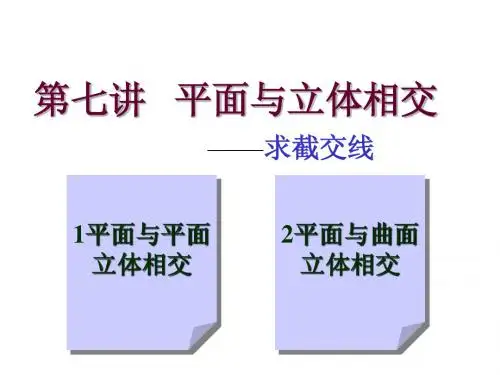
直线与立体形的相交关系与几何性质在几何学中，直线与立体形之间的相交关系对于研究和理解三维空间中的几何性质和图形重要性重大。

直线与不同类型的立体形（例如点、线段、射线、平面、立方体、圆柱体等）相交时，会涉及到不同的几何性质和特点。

一、直线与点的相交关系当一条直线与一个点相交时，它们只有一个交点。

无论点在直线上还是直线上的某个位置，交点都是这两个几何图形唯一的共同部分。

二、直线与线段的相交关系直线与线段的相交有三种情况：1. 直线与线段相交于线段的内部：当直线与线段的两个端点之间存在一个交点时，我们称直线与线段相交于线段的内部。

相交点既属于直线，也属于线段。

2. 直线与线段相交于线段的一个端点：当直线与线段的一个端点重合时，我们称直线与线段相交于线段的一个端点。

相交点仅属于直线与线段的共同部分。

3. 直线与线段不相交：当直线与线段没有任何交点时，我们称直线与线段不相交。

三、直线与射线的相交关系直线与射线的相交也有三种情况：1. 直线与射线相交于射线的起点：当直线与射线的起点重合时，我们称直线与射线相交于射线的起点。

相交点仅属于直线与射线的共同部分。

2. 直线与射线相交于射线的内部：当直线与射线之间存在一个交点时，我们称直线与射线相交于射线的内部。

相交点既属于直线，也属于射线。

3. 直线与射线不相交：当直线与射线没有任何交点时，我们称直线与射线不相交。

四、直线与平面的相交关系直线与平面的相交也存在几种情况：1. 直线与平面相交于一点：当直线与平面只有一个交点时，我们称直线与平面相交于一点。

2. 直线与平面平行：当直线与平面没有交点，且直线上的任何点到平面的最短距离都相等时，我们称直线与平面平行。

3. 直线与平面重合：当直线与平面是重合的，即直线在平面内部时，我们称直线与平面重合。

五、直线与立体形的相交关系直线与立体形的相交关系可能相对复杂，涉及到不同类型的立体形。

在与立体形相交时，直线可能穿过立体形、接触立体形的边界或者在立体形内部。

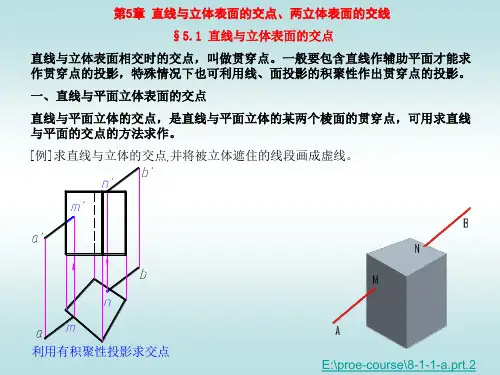
空间几何中的平面与立体形的相交关系概述：在空间几何中，平面与立体形的相交关系是一个重要的研究方向。

平面与立体形的相交关系不仅涉及到数学本身，也与物理、工程等领域密切相关。

本文将探讨平面与立体形的不同相交情况，并深入研究其几何性质和应用。

一、平面与平面相交：平面与平面相交是最简单的一种情况，可以分为平行和非平行两种情况。

当两个平面平行时，它们永远不会相交；当两个平面不平行时，它们会相交于一条直线。

这一性质在工程测量、建筑设计等领域具有广泛的应用。

二、平面与直线相交：平面与直线相交是平面几何中常见的情况。

当平面与直线相交时，它们的交点为一点。

通过求解平面与直线的方程，可以得到交点的坐标。

这一性质在数学中被广泛运用于解析几何的推导和证明。

三、平面与球体相交：平面与球体相交是空间几何中的一个重要问题。

当一个平面与一个球体相交时，可能存在以下三种情况：平面与球体相切于一点、相切于一个圆或者相交于两个交点。

根据不同情况，可以进一步讨论平面和球体的切线、交点等几何性质。

四、平面与圆柱相交：平面与圆柱相交也是几何学中的常见问题。

当一个平面与一个圆柱相交时，可能存在以下几种情况：相切于一个点、相交于一个圆或者相交于两个交线。

这一性质在建筑设计、机械工程等领域具有广泛的应用。

五、平面与圆锥相交：平面与圆锥相交是空间几何中的一个有趣问题。

当一个平面与一个圆锥相交时，可能存在以下几种情况：相切于一个点、相交于一个圆或者相交于两个交线。

通过研究平面和圆锥的相交性质，可以深入理解圆锥几何学中的一些基本概念和定理。

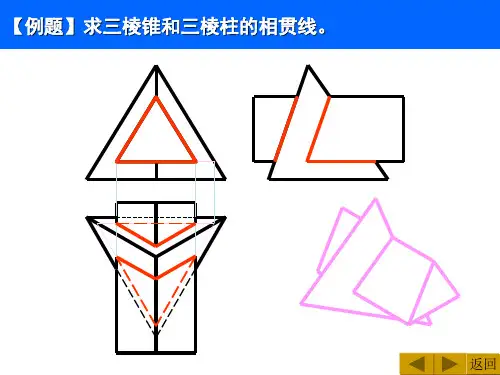
六、平面与多面体相交：平面与多面体相交是几何学中的一个复杂问题。

多面体包括了诸如立方体、正四面体、正六面体等形状，它们与平面的相交关系具有一定的规律性。

通过研究平面和多面体的相交性质，可以在计算机图形学、空间分析等领域中得到广泛应用。

七、应用领域：平面与立体形的相交关系在各个领域都有广泛的应用。

在建筑设计中，平面与立体形的相交关系决定了建筑物的外观和结构；在工程测量中，平面与立体形的相交关系决定了各种测量数据的获取方式；在计算机图形学中，平面与立体形的相交关系决定了虚拟场景的呈现效果。

《画法几何》课程标准课程名称：画法几何课程编码：0804100 学分：2.5 总学时：45适用专业：建筑设计技术一、前言1.课程性质《画法几何》课程是建筑设计技术专业必修的专业基础能力课程，是一门理论课程。

研究在平面上用图形表示形体和解决空间几何问题的理论和方法的学科。

本门课程在第1学期开设，先修课程是《立体几何》，建立良好的空间思维，后续课程是《建筑制图》等课程。

2．基本理念利用多媒体技术、CAI课件和网络视频等直观的教具，充分调动学生的学习积极性和主动性，在授课中常采用课堂提问、讨论、师生互动的形式来提高学生分析问题、解决问题的能力。

由于本课程实践性强，因此授课中穿插安排适量的习题课，“精讲多练”，指导学生及时消化和巩固所学的知识。

使之掌握好本学科的基本理论、基本知识和基本技能，并培养学生的动手能力。

3．设计思路《画法几何》课程是建筑类专业必修的专业基础课程。

课程内容结构分为三部分：制图基础、画法几何和投影制图，理论与实践比例约1：1，实践主要指课堂练习，课时为45学时，学分为2.5，考核评价方式分成两部分，即闭卷笔试占70％，平时作业、课堂提问、测试等占30％。

二、课程目标1．总体目标培养学生的制图技能和空间想象能力，为学生学习后续课程、完成课程设计和毕业设计打下必要的基础。

2．具体目标知识目标①能描述工程制图的国家标准规范，能正确使用绘图工具；②能绘制点、线、面、体的三面投影；③能绘制正等轴测图和斜二轴测图。

能力目标①能绘制和阅读简单建筑工程图样；②具有空间几何问题的图解能力；③具有空间想象能力和分析能力。

素质目标①具有自学能力；②具有分析问题和解决问题能力；③具有创造能力；④具有几何审美能力。

三、内容标准（课程内容与要求）四、实施建议1．教学组织形式与实施建议在绘图室实施教学，主要采用多媒体教学方式，讲授、示范和练习相结合，融教、学、练于一体。

2．教材选用与编写建议选用或编写适合建筑类专业高职学生学习的教材，需有配套的练习册。