工程力学 理论力学 约束、自由度与广义坐标讲解
- 格式:ppt
- 大小:1.98 MB
- 文档页数:34






力学系统的自由度与约束分析在我们日常生活和工程技术的各个领域,力学系统无处不在。
从简单的机械装置到复杂的航空航天结构,理解力学系统的行为和特性对于设计、分析和优化至关重要。
而在力学系统的研究中,自由度和约束是两个核心概念,它们为我们揭示了系统的运动可能性和限制条件。
首先,让我们来理解一下什么是自由度。
简单地说,自由度就是确定一个系统在空间中的位置和姿态所需的独立变量的数目。
比如说,一个在空间中自由运动的质点,它可以在三个方向(x、y、z)上自由移动,所以它有三个自由度。
而对于一个刚体,不仅要考虑其质心的位置(三个自由度),还要考虑其绕三个坐标轴的转动(三个自由度),总共就有六个自由度。
那么约束又是什么呢?约束就是对系统自由度的限制条件。
约束可以分为几何约束和运动约束。
几何约束限制了系统中质点的几何位置关系。
比如,一根不可伸长的绳子连接的两个质点,它们之间的距离就被绳子的长度所约束。
运动约束则限制了质点速度之间的关系。
例如,一个轮子在地面上滚动,轮子与地面接触点的速度必须为零,这就是一种运动约束。
为了更清晰地分析力学系统的自由度和约束,我们可以通过一些具体的例子来进行探讨。
考虑一个简单的平面滑块,它可以在一个水平平面内自由滑动。
在这个例子中,我们可以选择滑块在平面内的坐标(x,y)作为描述其位置的变量,因此这个滑块具有两个自由度。
如果我们在平面上设置一个固定的障碍物,使得滑块不能进入某个区域,这就形成了一个几何约束,滑块的自由度就相应减少了。
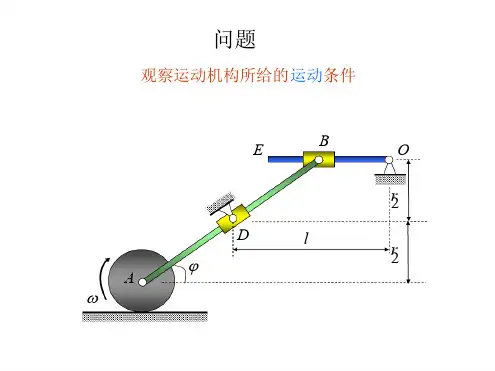
再来看一个更复杂一些的例子,比如一个由多个连杆组成的机构。
每个连杆都可以看作是一个刚体,具有六个自由度。
但是由于连杆之间通过铰链连接,这些铰链就对连杆的运动形成了约束。
通过对这些约束的分析,我们可以确定整个机构的自由度,从而了解其可能的运动方式。
在实际的工程应用中,对力学系统的自由度和约束进行准确分析具有重要意义。
在机械设计中,如果对自由度和约束的分析不准确,可能会导致设计的机构无法按照预期的方式运动,甚至出现卡死等故障。



第14章 虚位移原理在静力学中,我们利用力系的平衡条件研究了刚体在力的作用下的平衡问题,但对有许多约束的刚体系而言,求解某些未知力需要取几次研究对象,建立足够多的平衡方程,才能求出所要求的未知力。
这样做是非常繁杂,同时平衡方程的确立只是对刚体而言是必要和充分的条件;而对任意的非自由质点系而言,它只是必要条件不是充分条件。
从本章开始我们学习用数学分析的方法来研究非自由质点系的力学问题,称为分析力学。
1788年,法国科学家拉格朗日发表的《分析力学》一书,给出了解决非自由质点系的新方法,即利用广义坐标描述非自由质点系的运动,使描述系统运动量大大减少,同时从能量角度出发将质点系的动能、势能与功用广义坐标联系起来,给出了动力学普遍方程和拉格朗日方程。
虚位移原理是静力学的最一般原理,它给出了任意质点系平衡的必要和充分条件,减少了不必要的平衡方程,从系统主动力作功的角度出发研究质点系的平衡问题。
14.1 约束·自由度·广义坐标质点或质点系的运动受到它周围物体的限制作用,这种限制作用称为约束,表示约束的数学方程称为约束方程。
按约束方程的形式对约束进行以下分类。
1.几何约束和运动约束限制质点或质点系在空间的几何位置的条件称为几何约束。
例如图14-1所示的单摆,其约束方程为222l =y +x又如图14-2所示的曲柄连杆机构,其约束方程为⎪⎩⎪⎨⎧--0+22222=y l =)y (y +)x (x r =y x BB A 2B A A A图14-2xy图14-3上述例子中的约束方程均表示几何约束。
如果约束方程中含有坐标对时间的导数,或者说,约束限制质点或质点系运动的条件,称为运动约束。
例如图14-3所示在平直轨道上作纯滚动的圆轮,轮心C 的速度为ωr =v c运动约束方程为0=ωr v c -设c x 和φ分别为轮心C 点的坐标和圆轮的转角,则上式可改写为0C =r φx- 2.定常约束与非定常约束约束方程中不显含时间的约束称为定常约束,上面各例中的约束均为定常约束。