1-1_约束和广义坐标解析
- 格式:ppt
- 大小:1.20 MB
- 文档页数:1


广义坐标和约束体系在物理学和工程学中,广义坐标和约束体系是描述多体系统运动的重要工具。
广义坐标是一组描述系统状态的独立变量,而约束体系则是一组将系统中各个部分联系在一起的条件。
本文将介绍广义坐标的概念和应用,并探讨约束体系在多体系统动力学中的作用。
一、广义坐标的概念和应用在传统的牛顿力学中,我们常常使用笛卡尔坐标系来描述物体的位置和运动。
然而,在复杂的多体系统中,使用笛卡尔坐标系来描述每个质点的运动往往变得非常复杂。
为了简化问题,引入广义坐标的概念就显得尤为重要。
广义坐标是一组相互独立的变量,它们可以用来描述系统的状态。
与笛卡尔坐标不同的是,广义坐标可以是质点的位置坐标、质点的广义速度、质点的质心位置、刚体的欧拉角等等。
通过引入广义坐标,我们可以用更简洁的方式描述系统的状态,简化求解的过程。
广义坐标的应用十分广泛。
在理论物理中,广义坐标常常用于构建拉格朗日力学和哈密顿力学的数学框架。
在工程学中,广义坐标常常用于描述机械系统中各个零件的运动和变形。
例如,通过引入关节的旋转角度作为广义坐标,可以简化机械臂的运动学分析。
二、约束体系在多体系统动力学中的作用在多体系统中,各个质点之间通常存在一定的约束关系。
这些约束条件可以是几何约束(如刚度约束、长度约束等)或非几何约束(如速度约束、加速度约束等)。
约束体系是将约束条件用方程形式表示的系统。
约束体系在多体系统动力学中发挥着重要作用。
它可以用来限制系统的自由度,从而简化问题的求解。
通过引入拉格朗日乘子的方法,我们可以将约束条件与系统的动力学方程相结合,得到描述系统运动的广义拉格朗日方程。
在这个过程中,广义坐标发挥了重要的作用,它将系统状态映射到一个更简洁的空间中。
约束体系还可以用来分析系统的稳定性和振动特性。
通过线性化约束方程,我们可以得到系统的模态分析,从而了解系统的固有振动频率和模式形态。
这对于设计和优化振动系统非常重要。
三、结论广义坐标和约束体系在多体系统的描述和分析中起到了至关重要的作用。
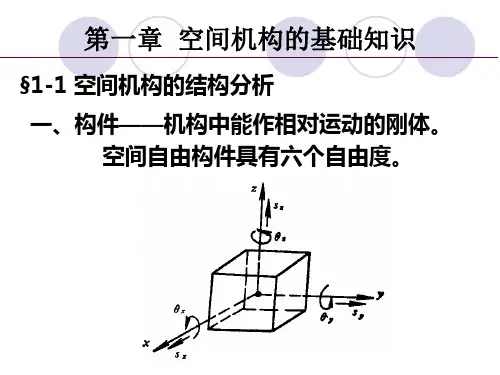







第14章 虚位移原理在静力学中,我们利用力系的平衡条件研究了刚体在力的作用下的平衡问题,但对有许多约束的刚体系而言,求解某些未知力需要取几次研究对象,建立足够多的平衡方程,才能求出所要求的未知力。
这样做是非常繁杂,同时平衡方程的确立只是对刚体而言是必要和充分的条件;而对任意的非自由质点系而言,它只是必要条件不是充分条件。
从本章开始我们学习用数学分析的方法来研究非自由质点系的力学问题,称为分析力学。
1788年,法国科学家拉格朗日发表的《分析力学》一书,给出了解决非自由质点系的新方法,即利用广义坐标描述非自由质点系的运动,使描述系统运动量大大减少,同时从能量角度出发将质点系的动能、势能与功用广义坐标联系起来,给出了动力学普遍方程和拉格朗日方程。
虚位移原理是静力学的最一般原理,它给出了任意质点系平衡的必要和充分条件,减少了不必要的平衡方程,从系统主动力作功的角度出发研究质点系的平衡问题。
14.1 约束·自由度·广义坐标质点或质点系的运动受到它周围物体的限制作用,这种限制作用称为约束,表示约束的数学方程称为约束方程。
按约束方程的形式对约束进行以下分类。
1.几何约束和运动约束限制质点或质点系在空间的几何位置的条件称为几何约束。
例如图14-1所示的单摆,其约束方程为222l =y +x又如图14-2所示的曲柄连杆机构,其约束方程为⎪⎩⎪⎨⎧--0+22222=y l =)y (y +)x (x r =y x BB A 2B A A A图14-2xy图14-3上述例子中的约束方程均表示几何约束。
如果约束方程中含有坐标对时间的导数,或者说,约束限制质点或质点系运动的条件,称为运动约束。
例如图14-3所示在平直轨道上作纯滚动的圆轮,轮心C 的速度为ωr =v c运动约束方程为0=ωr v c -设c x 和φ分别为轮心C 点的坐标和圆轮的转角,则上式可改写为0C =r φx- 2.定常约束与非定常约束约束方程中不显含时间的约束称为定常约束,上面各例中的约束均为定常约束。
广义坐标通俗解释
广义坐标是用来描述系统位形所需要的独立参数,或者最少参数。
当分析有的问题时(尤其是当有许多约束条件的时候),尽量选择独立的广义坐标。
因为这样可以减少代表约束的变量。
但是,当遇到非完整约束时,或者当计算约束力时,就必须使用关于这约束力的,相应的广义坐标。
广义坐标是不特定的坐标。
假若,我们用一组广义坐标来导引方程,所得到的答案,可以应用于较广泛的问题;并且,当我们最后终于设定这坐标时,答案仍旧是正确的。
拉格朗日力学,哈密顿力学都需要用到广义坐标来表示基要概念与方程。
常用的广义坐标有线量和角量两种。
例如,对约束在空间固定曲线上运动的质点,可用自始点计量的路程s作广义坐标;用细杆约束在竖直平面内摆动的质点,可用杆与铅垂线的夹角θ作广义坐标。
广义坐标对时间的导数称广义速度。
同样,因为问题需要也会有广义加速度、广义动量、广义角动量等。
1。
約瑟夫∙拉格朗日拉格朗日力学维基百科,自由的百科全书拉格朗日力学(英语:Lagrangian mechanics )是分析力学中的一种,于1788年由約瑟夫∙拉格朗日所创立。
拉格朗日力学是对经典力学的一种的新的理论表述,着重于数学解析的方法,並運用最小作用量原理[1],是分析力学的重要组成部分。
经典力学最初的表述形式由牛顿建立,它着重於分析位移,速度,加速度,力等矢量间的关系,又称为矢量力学。
拉格朗日引入了广义坐标的概念,又运用达朗贝尔原理,求得与牛顿第二定律等价的拉格朗日方程。
不仅如此,拉格朗日方程具有更普遍的意义,适用范围更广泛。
还有,选取恰当的广义坐标,可以大大地简化拉格朗日方程的求解过程。
目录1自由度2广义坐标3拉格朗日量4拉格朗日方程5拉格朗日力学的扩展6参见7参考文献自由度力学系统可以由一组坐标来描述。
例如,一个质点的运动(在笛卡尔坐标系中)由x 、y 、z 三个坐标来描述。
一般而言,个质点组成的力学系统由个坐标来描述。
力学系统中常常存在着各种约束,使得这个坐标并不都是独立的。
力学系统的独立坐标的个数称之为自由度。
对于个质点组成的力学系统,若存在个约束,则系统的自由度为。
广义坐标在矢量力学中,约束的存在体现于作用于系统的约束力。
约束力引入额外的未知量,通常使问题变得更为复杂。
但若能选取适当的个完全满足约束条件的独立坐标,则约束不再出现在问题中,只需要求解关于个未知变量的方程,使问题得以大大简化。
而如果运用牛顿力学来解约束问题,通常约束越多,需要求解的方程个数就越多,反而增加了一定的难度。
这样的个坐标不再局限于各质点的位置坐标,而可以是任何能描述系统的几何参量,因此称为“广义坐标”。
拉格朗日量拉格朗日力学的一个基本假设是:具有个自由度的系统,其运动状态完全由个广义坐标及广义速度决定。
或者说,力学系统的运动状态由一个广义坐标和广义速度的函数描述:。
这个函数称为拉格朗日函数或拉格朗日量。
引入势能函数[2]。