工程力学 理论力学 约束、自由度与广义坐标
- 格式:ppt
- 大小:1.98 MB
- 文档页数:34

《工程力学Ⅰ》课程教学大纲课程编号:125111 学分: 4 (4学时/周) 总学时:68大纲执笔人:陈洁大纲审核人:王斌耀一、课程性质与目的工程力学(Ⅰ)(包括静力学、材料力学两部分)是土木工程专业的一门重要的技术基础课,它是各门后续课程的基础,并在许多工程技术领域中有着广泛的应用。
本课程的目的是使学生掌握静力学中一般力系的简化与平衡问题的分析介绍方法;掌握材料力学中构件在拉、压、剪切、扭转和弯曲时的强度与刚度问题的分析计算方法,构件在组合变形时的强度与刚度问题的分析计算方法,以及构件在受压时稳定性问题的分析计算方法等;掌握材料的基本力学性能和基本的材料力学实验方法;初步学会应用基本概念、基本理论和基本分析方法去分析问题和解决问题,为学习一系列后继课程打好必要的基础。
同时结合本课程的特点培养学生分析、解决工程实际问题的能力,提高学生的综合素质。
二、课程基本要求1、掌握力的概念、力的投影和力矩的计算;2、掌握力系简化的方法和一般的简化结果;3、掌握刚体静力学的平衡条件和平衡方程;4、对材料力学的基本概念和基本的分析方法有明确的认识。
5、具有将简单受力杆件简化为力学简图的初步能力,具有力学建模的初步概念与能力。
6、能熟练地做出杆件在基本变形下的内力图、计算其应力和位移、并进行强度和刚度计算。
7、对应力状态理论和强度理论有明确的认识,并能将其应用于组合变形下杆件的强度计算。
8、理解掌握简单超静定问题的求解方法。
9、对能量法的有关基本原理有明确认识,并熟练地掌握一种计算位移的能量方法。
10、对压杆的稳定性概念有明确的认识,能熟练计算轴向受压杆的临界载荷与临界应力,并进行稳定性校核等计算。
11、掌握质点系的质心、刚体的转动惯量、惯性积、惯性主轴和惯性积的平行移轴公式;掌握截面的静矩,形心的位置,惯性矩和惯性积及它们的平行移轴公式,转轴公式。
组合截面的惯性矩、惯性积计算,截面的形心主惯性轴和形心主惯性矩的计算11、对于常用材料在常温下的基本力学性能及其测试方法有初步认识。






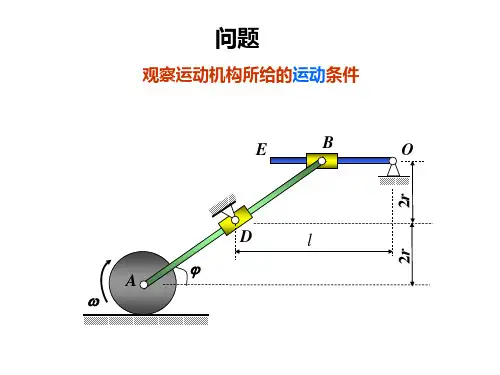


理论力学约束及其分类在第一篇静力学中,我们从静力学公理出发,通过力系 的简化,得出刚体的平衡条件,用来研究刚体及刚体系统的 平衡问题。
在这一章里,我们将介绍普遍适用于研究任意质 点系的平衡问题的一个原理,它从位移和功的概念出发,得 出任意质点系的平衡条件。
该原理叫做虚位移原理。
它是研 究平衡问题的最一般的原理,不仅如此,将它与达兰贝尔原 理相结合,就可得到一个解答动力学问题的动力学普遍方程。
一、约束及约束方程 限制质点或质点系运动的各种条件称为约束。
将约束的限制条件以数学方程来表示,则称为约束方程。
例如:平 x 2+y 2=l 2x 2 +y 2=r 2A A -y )2=l 2,y =0AB (x -x )2+(y B AB 二、约束的分类 根据约束的形式和性质,可将约束划分为不同的类型,通常按如下分类:1.几何约束和运动约束限制质点系在空间几何位置的条件称为几何约束。
如前述的平 和 例子中的限制条件 都是几何约束。
几何约束方程的一般形式为f r (x 1, y 1, z 1,×××, x n , y n , z n ) = 0当约束对质点系的运动情况进行限制时,这种约束 条件称为运动约束。
运动约束方程的一般形式为f r (x 1, y 1, z 1,×××, x n , y n , z n , x &1, y &1, z &1,×××, x &n , y &n , z &n ) = 0约束条件不 时间 的约束为 常约束。
当约束条件与时间 , 时间 化时称为 常约束。
前 的例子中约束条件 不 时间 化,它们都是 常约束。
例如: M 一条 过 的系 。
时 l 0, v动 子。
运动约束:v A -r ω=02. 常约束和 常约束x 2+y 2=(l 0-vt )2约束方程中 时间t 几何约束:y A =r例如: 动时。