(完整版)云模型matlab程序

进行通信系统的建模、仿真和分析。
谢谢聆听
B
C
变量与赋值
在MATLAB中，变量不需要事先声明，可以 直接赋值。变量名以字母开头，可以包含字 母、数字和下划线。
常用函数
MATLAB提供了丰富的内置函数，如sin、 cos、tan等三角函数，以及abs、sqrt等数 学函数。用户可以通过help命令查看函数的
D
使用方法。
02 矩阵运算与数组操作
错误处理
阐述try-catch错误处理机制的语法、 执行流程及应用实例。
04
函数定义与调用
函数概述
阐述函数的概念、作用及分类，包括内置函数和 自定义函数。
函数调用
深入剖析函数的调用方法，包括直接调用、间接 调用及参数传递等技巧。
ABCD
函数定义
详细讲解自定义函数的定义方法，包括函数名、 输入参数、输出参数及函数体等要素。
拟合方法
利用已知数据点构造近似函数，如最小二乘法、多项 式拟合、非线性拟合等。
插值与拟合的比较
插值函数经过所有数据点，而拟合函数则追求整体上 的近似。
数值积分与微分
01
数值积分方法
利用数值技术计算定积分的近似 值，如矩形法、梯形法、辛普森 法等。
02
数值微分方法
通过数值技术求解函数的导数或 微分，如差分法、中心差分法、 五点差分法等。
02
01
矩阵运算
加法与减法
对应元素相加或相减，要求矩阵 大小相同
乘法
使用`*`或`mtimes`函数进行矩阵 乘法，要求内维数相同
点乘与点除
使用`.*`、`./`进行对应元素相乘或 相除，要求矩阵大小相同
特征值与特征向量

matlab建模教程Matlab是一种强大的数学建模和仿真平台，广泛应用于科学、工程和金融领域。

本教程将介绍如何使用Matlab进行建模，并详细解释每个步骤。

首先，我们需要了解什么是建模。

建模是根据实际问题或系统的特性创建数学模型的过程。

这些数学模型可以帮助我们理解系统的行为并预测未来的结果。

使用Matlab进行建模可以简化模型的创建和分析过程。

在Matlab中，我们可以使用一个称为“脚本”的文件来编写和运行建模代码。

脚本是一系列Matlab命令的集合，这些命令可以被连续执行以创建所需的模型。

为了方便起见，我们可以在Matlab编辑器中创建和编辑脚本。

建模的第一步是定义问题。

要定义问题，我们需要确定所建模型的目标、输入和输出。

例如，如果我们想建立一个温度预测模型，我们需要明确模型的输入是什么（例如，环境条件）和输出是什么（例如，预测的温度值）。

接下来，我们需要收集数据。

收集数据是为了分析和验证我们的模型。

在Matlab中，我们可以使用数据存储和处理工具，如表格和数据数组，来导入和处理数据。

一旦我们有了数据，我们就可以开始建立模型。

在Matlab中，我们可以使用数学方程、统计方法和机器学习算法等多种方法来建立模型。

例如，我们可以使用线性回归来拟合数据，或者使用神经网络进行分类。

建立模型后，我们可以使用Matlab的可视化工具来分析模型的输出。

Matlab提供了各种绘图函数，如plot和scatter，来绘制图形并展示模型的结果。

我们可以使用这些图形来比较实际数据与模型的预测结果。

最后，我们可以优化我们的模型。

通过调整模型的参数和改进算法，我们可以提高模型的性能和准确性。

在Matlab中，我们可以使用遗传算法、粒子群优化和模拟退火等算法来优化我们的模型。

在建模过程中，我们还需要注意一些常见的问题和错误。

例如，过拟合是一种常见的问题，指的是模型过度适应训练数据，导致对新数据的预测效果较差。

为了避免过拟合，我们可以使用交叉验证和正则化等技术。

矩阵的数学运算
总结词
详细描述
总结词
详细描述
掌握矩阵的数学运算，如求逆 、求行列式、求特征值等。
在MATLAB中，可以使用inv() 函数来求矩阵的逆，使用det() 函数来求矩阵的行列式，使用 eig()函数来求矩阵的特征值。 例如，A的逆可以表示为 inv(A)，A的行列式可以表示 为det(A)，A的特征值可以表 示为eig(A)。
• 总结词：了解特征值和特征向量的概念及其在矩阵分析中的作用。 • 详细描述：特征值和特征向量是矩阵分析中的重要概念。特征值是满足Ax=λx的标量λ和向量x，特征向量是与特征值对
应的非零向量。特征值和特征向量在许多实际问题中都有应用，如振动分析、控制系统等。
04
MATLAB图像处理
图像的读取与显示
变量定义
使用赋值语句定义变量，例如 `x = 5`。
矩阵操作
学习如何创建、访问和操作矩 阵，例如使用方括号 `[]`。
函数编写
学习如何创建自定义函数来执 行特定任务。
02
MATLAB编程
变量与数据类型
01
02
03
变量命名规则
MATLAB中的变量名以字 母开头，可以包含字母、 数字和下划线，但不应与 MATLAB保留字冲突。
了解矩阵的数学运算在实际问 题中的应用。
矩阵的数学运算在许多实际问 题中都有应用，如线性方程组 的求解、矩阵的分解、信号处 理等。通过掌握这些运算，可 以更好地理解和解决这些问题 。
矩阵的分解与特征值
• 总结词：了解矩阵的分解方法，如LU分解、QR分解等。
• 详细描述：在MATLAB中，可以使用lu()函数进行LU分解，使用qr()函数进行QR分解。这些分解方法可以将一个复杂的 矩阵分解为几个简单的部分，便于计算和分析。

控制流语句
使用条件语句（如if-else）和 循环语句（如for）来控制程序 流程。
变量定义
使用赋值语句定义变量，例如 `a = 5`。
矩阵运算
使用矩阵进行数学运算，如加 法、减法、乘法和除法等。
函数编写
创建自定义函数来执行特定任 务。
02
MATLAB编程语言基础
变量与数据类型
变量命名规则
数据类型转换
编辑器是一个文本编辑器 ，用于编写和编辑 MATLAB脚本和函数。
工具箱窗口提供了一系列 用于特定任务的工具和功 能，如数据可视化、信号 处理等。
工作空间窗口显示当前工 作区中的变量，可以查看 和修改变量的值。
MATLAB基本操作
数据类型
MATLAB支持多种数据类型， 如数值型、字符型和逻辑型等 。
04
MATLAB数值计算
数值计算基础
01
02
03
数值类型
介绍MATLAB中的数值类 型，包括双精度、单精度 、复数等。
变量赋值
讲解如何给变量赋值，包 括标量、向量和矩阵。
运算符
介绍基本的算术运算符、 关系运算符和逻辑运算符 及其优先级。
数值计算函数
数学函数
列举常用的数学函数，如 三角函数、指数函数、对 数函数等。
矩阵的函数运算
总结词：MATLAB提供了许多内置函 数，可以对矩阵进行各种复杂的运算
。
详细描述
矩阵求逆：使用 `inv` 函数求矩阵的 逆。
特征值和特征向量：使用 `eig` 函数 计算矩阵的特征值和特征向量。
行列式值：使用 `det` 函数计算矩阵 的行列式值。
矩阵分解：使用 `factor` 和 `expm` 等函数对矩阵进行分解和计算指数。

全局变量
全局变量(Global Variables)是可以在不同的函数工作空间和MATALB工作空间中共享使用的变量。 用 global定义, 而且每个要共享全局变量的函数和工作空间,都必须逐个定义, 先定义后使用. 注意：由于全局变量在任何定义过的函数中都可以修改，因此不提倡使用全局变量；使用时应十分小心，建议把全局变量的定义放在函数体的开始，全局变量用大写字符命名。
M函数文件的基本格式
函数声明行
function [输出变量列表] = 函数名(输入变量列表)
H1行(用%开头的注释行) 在线帮助文本 (用%开头) 编写和修改记录(用%开头)
函数体
创建M函数文件并调用的步骤
编写函数代码 将函数文件保存为“函数名.m”。 在命令窗口输入命令调用程序
利用泛函命令求极小值
2. fminsearch函数 ：求多变量无约束非线性最小值。 x=fminsearch(h_fun,x0) x=fminsearch(‘funname’,x0) x0是最小值点的初始猜测值。
其它泛函命令
3 .fzero函数：求一维函数的零点，即求f(x)=0的根。 x=fzero(h_fun, x0, tol, trace) x=fzero(‘funname’, x0, tol, trace) x0有两个作用：预定待搜索零点的大致位置和搜索起始点；tol用来控制结果的相对精度，默认值为eps；trace指定迭代信息是否在运算中显示。
其它泛函命令
4. 数值积分：quad和quad8是基于数学上的正方形概念来计算函数的面积。 5. 微分方程的数值解：MATLAB提供ode23、ode45和ode113等多个函数求解微分方程的数值解。
泛函命令
在MATLAB中，所有以函数为输入变量的命令，都称为泛函命令。

MATLAB模型构建与优化方法介绍一、引言MATLAB（Matrix Laboratory）是一种强大而灵活的数值计算与数据可视化软件，广泛应用于科学、工程、金融等各个领域。

在模型构建与优化方面，MATLAB提供了丰富的工具和函数，使得用户可以方便地进行模型构建和参数优化。

二、MATLAB模型构建在MATLAB中，模型构建是指通过定义变量、方程和约束条件，将实际问题转化为数学模型。

MATLAB提供了多种方式来构建模型，其中最常用的是使用符号运算工具箱。

符号运算工具箱提供了符号计算的功能，可以在MATLAB中创建符号变量、符号函数和符号表达式。

用户可以使用符号计算工具箱对数学公式进行展开、求导、积分等操作，从而方便地构建数学模型。

例如，我们可以使用符号计算工具箱来构建一个简单的线性回归模型。

首先，创建符号变量x和y，表示输入和输出变量。

然后，定义线性模型的表达式为y =a*x + b，其中a和b为待求参数。

最后，通过最小二乘法等方法，可以求解出最优的参数值。

除了符号运算工具箱外，MATLAB还提供了其他模型构建工具，如优化工具箱、神经网络工具箱等。

用户可以根据具体需求选择合适的工具进行模型构建。

三、MATLAB模型优化模型优化是指通过调整模型参数，使得模型能够更好地拟合实际数据或达到最优性能。

MATLAB提供了多种优化方法，包括数值优化、遗传算法、模拟退火等。

1. 数值优化数值优化是一类通过迭代求解数值问题的方法。

MATLAB中的数值优化工具箱提供了多种数值优化算法，包括最小二乘法、非线性规划、最大似然估计等。

用户可以根据具体情况选择合适的算法进行优化。

例如，我们可以使用最小二乘法来优化线性回归模型中的参数。

最小二乘法通过最小化实际输出与模型输出之间的误差平方和，来得到最优的参数估计。

MATLAB中的lsqcurvefit函数可以方便地进行最小二乘法优化，用户只需提供模型函数和初始参数值即可。

2. 遗传算法遗传算法是一种模拟生物进化过程的启发式优化算法。

matlab教程 PPT(完整版)
汇报人：可编辑
2023-12-24
目录
• MATLAB基础 • MATLAB编程 • MATLAB矩阵运算 • MATLAB数值计算 • MATLAB可视化 • MATLAB应用实例
01
CATALOGUE
MATLAB基础
MATLAB简介
MATLAB定义
MATLAB应用领域
菜单栏
包括文件、编辑、查看、主页 、应用程序等菜单项。
命令窗口
用于输入MATLAB命令并显示 结果。
MATLAB主界面
包括命令窗口、当前目录窗口 、工作空间窗口、历史命令窗 口等。
工具栏
包括常用工具栏和自定义工具 栏。
工作空间窗口
显示当前工作区中的变量。
MATLAB基本操作
变量定义
使用变量名和赋值符号（=）定义变 量。
详细描述
直接输入：在 MATLAB中，可以直 接通过输入矩阵的元 素来创建矩阵。例如 ，`A = [1, 2, 3; 4, 5, 6; 7, 8, 9]`。
使用函数创建： MATLAB提供了多种 函数来创建特殊类型 的矩阵，如`eye(n)`创 建n阶单位矩阵， `diag(v)`创建由向量v 的元素构成的对角矩 阵。
使用bar函数绘制柱状图 ，可以自定义柱子的宽
度、颜色和标签。
使用pie函数绘制饼图， 可以自定义饼块的比例
和颜色。
三维绘图
01
02
03
04
三维线图
使用plot3函数绘制三维线图 ，可以展示三维空间中的数据
点。
三维曲面图
使用surf函数绘制三维曲面图 ，可以展示三维空间中的曲面
。
三维等高线图

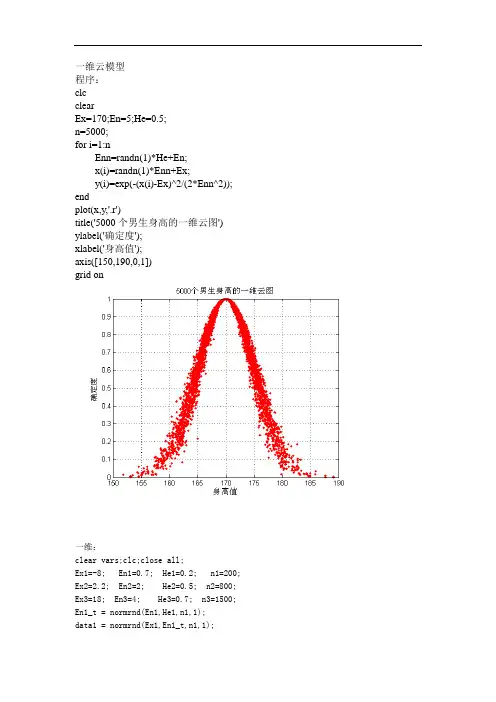
一维云模型程序：clcclearEx=170;En=5;He=0.5;n=5000;for i=1:nEnn=randn(1)*He+En;x(i)=randn(1)*Enn+Ex;y(i)=exp(-(x(i)-Ex)^2/(2*Enn^2)); endplot(x,y,'.r')title('5000个男生身高的一维云图') ylabel('确定度');xlabel('身高值');axis([150,190,0,1])grid on一维：clear vars;clc;close all;Ex1=-8; En1=0.7; He1=0.2; n1=200; Ex2=2.2; En2=2; He2=0.5; n2=800; Ex3=18; En3=4; He3=0.7; n3=1500; En1_t = normrnd(En1,He1,n1,1);data1 = normrnd(Ex1,En1_t,n1,1);mu1 = exp(-0.5*((data1-Ex1)./En1_t).^2);En2_t = normrnd(En2,He2,n2,1);data2 = normrnd(Ex2,En2_t,n2,1);mu2 = exp(-0.5*((data2-Ex2)./En2_t).^2);En3_t = normrnd(En3,He3,n3,1);data3 = normrnd(Ex3,En3_t,n3,1);mu3 = exp(-0.5*((data3-Ex3)./En3_t).^2);figure(1);plot(data1,mu1,'.b',data2,mu2,'*r',data3,mu3,'+k'); axis equal;二维云模型程序：clcclearEx1=170;En1=5;He1=0.5;Ex2=65;En2=3;He2=0.2;n=5000;for i=1:nEnn1=randn(1)*He1+En1;x1(i)=randn(1)*Enn1+Ex1;Enn2=randn(1)*He2+En2;x2(i)=randn(1)*Enn2+Ex2;y(i)=exp(-(x1(i)-Ex1)^2/(2*Enn1^2)-(x2(i)-Ex2)^2/(2*Enn2^2)); endplot3(x1,x2,y,'.r')title('5000个男生身高体重的二维云图')axis([148,190,50,80,0,1])grid on结果：多个一维clear vars;clc;close all;Ex1=0; En1=0.103; He1=0.013; n1=5000;Ex2=0.309; En2=0.064; He2=0.008; n2=5000;Ex3=0.5; En3=0.039; He3=0.005; n3=5000;Ex4=0.691; En4=0.064; He4=0.008; n4=5000;Ex5=1; En5=0.103; He5=0.013; n5=5000;En1_t = normrnd(En1,He1,n1,1);data1 = normrnd(Ex1,En1_t,n1,1);mu1 = exp(-0.5*((data1-Ex1)./En1_t).^2);En2_t = normrnd(En2,He2,n2,1);data2 = normrnd(Ex2,En2_t,n2,1);mu2 = exp(-0.5*((data2-Ex2)./En2_t).^2);En3_t = normrnd(En3,He3,n3,1);data3 = normrnd(Ex3,En3_t,n3,1);mu3 = exp(-0.5*((data3-Ex3)./En3_t).^2);En4_t = normrnd(En4,He4,n4,1);data4 = normrnd(Ex4,En4_t,n4,1);mu4 = exp(-0.5*((data4-Ex4)./En4_t).^2);En5_t = normrnd(En5,He5,n5,1);data5 = normrnd(Ex5,En5_t,n5,1);mu5 = exp(-0.5*((data5-Ex5)./En5_t).^2);figure(1);plot(data1,mu1,'.r',data2,mu2,'.r',data3,mu3,'.r',data4,mu4,'.r',data5,mu5,'.r' );title('评价集')ylabel('隶属度');axis([-0.4,1.4,0,1])grid on一维Ex=1100;En=84.926;He=0.1;n=1000;X=zeros(1,n);Y=zeros(1,n);X(1:n)=normrnd(En,He,1,n);for i=1:nEn1=X(1,i);X(1,i)=normrnd(Ex,En1,1);Y(1,i)=exp((-(X(1,i)-Ex)^2)/(2*En1^2));plot(X,Y,'.','MarkerEdgeColor','k','markersize',4); title('强等级','fontsize',16);grid on;end逆发生器代码X1=X ;Y1=Y;i=1;while i<=(n-flag)If Y1(1,i)>0.9999Y1(:,i)=[ ] ;X1(:,i)=[ ] ;flag=flag+1;End;Ex=mean(X1) ;En1=zeros(1,m) ;for i=1:m ;En1(1,i)=abs(X1(1,i)-Ex)/sqrt(-2*log(Y1(1,i))) ; End ;En=mean(En1) ;He=0 ;for i=1:m ;He=He+(En1(1,i)-En)^2 ;He=sqrt(He/(m-1)) ;End ;X1 =X;Y1=Y;i=1;while i<=(n-flag)if Y1(1,i)>0.9999Y1(:,i)=[];X1(:,i)=[];flag=flag+1;elsei=i+1;m=m +1;endendEx=mean(X1)En1=zeros(1,m);for i= l:mEn1(1,i)=abs(X1(1,i)-Ex)/sqrt(-2 *log(Y1(1,i))); endEn=mean(En1);He=0;for i=l:mHe=He+(En1(1,i)-En)^2;endHe=sqrt(He/(m-1))clear vars;clc;close all;Ex1=0.457; En1=0.150; He1=0.050; n1=4000; Ex2=0.454; En2=0.156; He2=0.056; n2=4000;Ex3=0.435; En3=0.229; He3=0.067; n3=4000;Ex4=0.415; En4=0.177; He4=0.071; n4=4000;Ex5=0.414; En5=0.298; He5=0.099; n5=4000; Ex6=0.410; En6=0.242; He6=0.061; n6=4000;Ex7=0.410; En7=0.188; He7=0.061; n7=4000;Ex8=0.500; En8=0.039; He8=0.005; n8=5000;En1_t = normrnd(En1,He1,n1,1);data1 = normrnd(Ex1,En1_t,n1,1);mu1 = exp(-0.5*((data1-Ex1)./En1_t).^2);En2_t = normrnd(En2,He2,n2,1);data2 = normrnd(Ex2,En2_t,n2,1);mu2 = exp(-0.5*((data2-Ex2)./En2_t).^2);En3_t = normrnd(En3,He3,n3,1);data3 = normrnd(Ex3,En3_t,n3,1);mu3 = exp(-0.5*((data3-Ex3)./En3_t).^2);En4_t = normrnd(En4,He4,n4,1);data4 = normrnd(Ex4,En4_t,n4,1);mu4 = exp(-0.5*((data4-Ex4)./En4_t).^2);En5_t = normrnd(En5,He5,n5,1);data5 = normrnd(Ex5,En5_t,n5,1);mu5 = exp(-0.5*((data5-Ex5)./En5_t).^2);En6_t = normrnd(En6,He6,n6,1);data6 = normrnd(Ex6,En6_t,n6,1);mu6 = exp(-0.5*((data6-Ex6)./En6_t).^2);En7_t = normrnd(En7,He7,n7,1);data7 = normrnd(Ex7,En7_t,n7,1);mu7 = exp(-0.5*((data7-Ex7)./En7_t).^2);En8_t = normrnd(En8,He8,n8,1);data8 = normrnd(Ex8,En8_t,n8,1);mu8 = exp(-0.5*((data8-Ex8)./En8_t).^2);figure(1);plot(data1,mu1,'.r',data2,mu2,'.r',data3,mu3,'.r',data4,mu4,'.r',data5,mu5,'.r' ,data6,mu6,'.r',data7,mu7,'.r',data8,mu8,'.r');title('评价集')ylabel('隶属度');axis([-0.4,1.4,0,1])grid onclear vars;clc;close all;Ex1=0.716; En1=0.123; He1=0.045; n1=4000;Ex2=0.545; En2=0.140; He2=0.052; n2=4000;Ex3=0.534; En3=0.233; He3=0.085; n3=4000;Ex4=0.461; En4=0.202; He4=0.063; n4=4000;Ex5=0.691; En5=0.064; He5=0.008; n5=6000;En1_t = normrnd(En1,He1,n1,1);data1 = normrnd(Ex1,En1_t,n1,1);mu1 = exp(-0.5*((data1-Ex1)./En1_t).^2);En2_t = normrnd(En2,He2,n2,1);data2 = normrnd(Ex2,En2_t,n2,1);mu2 = exp(-0.5*((data2-Ex2)./En2_t).^2);En3_t = normrnd(En3,He3,n3,1);data3 = normrnd(Ex3,En3_t,n3,1);mu3 = exp(-0.5*((data3-Ex3)./En3_t).^2);En4_t = normrnd(En4,He4,n4,1);data4 = normrnd(Ex4,En4_t,n4,1);mu4 = exp(-0.5*((data4-Ex4)./En4_t).^2);En5_t = normrnd(En5,He5,n5,1);data5 = normrnd(Ex5,En5_t,n5,1);mu5 = exp(-0.5*((data5-Ex5)./En5_t).^2);figure(1);plot(data1,mu1,'.r',data2,mu2,'.r',data3,mu3,'.r',data4,mu4,'.r',data5,mu5,'.r' );title('评价集')ylabel('隶属度');axis([-0.4,1.4,0,1]) grid on。

（完整版）Matlab⼊门教程第1章MATLAB操作基础1.1 MATLAB概述1.1.2 MATLAB的主要功能1．数值计算MATLAB以矩阵作为数据操作的基本单位，还提供了⼗分丰富的数值计算函数。

2．绘图功能可以绘制⼆维、三维图形，还可以绘制特殊图形（与统计有关的图，例如：区域图、直⽅图、饼图、柱状图等）。

3．编程语⾔MATLAB具有程序结构控制、函数调⽤、数据结构、输⼊输出、⾯向对象等程序语⾔特征，⽽且简单易学、编程效率⾼。

4．MATLAB⼯具箱MATLAB包含两部分内容：基本部分和各种可选的⼯具箱。

MATLAB⼯具箱分为两⼤类：功能性⼯具箱和学科性⼯具箱。

1.1.3MATLAB语⾔的特点语⾔简洁紧凑，使⽤⽅便灵活，易学易⽤。

例如：A=[1 2 3;4 5 6;7 8 9]⼀条语句实现了对3x3矩阵的输⼊。

语句功能强⼤，⼀条语句相当于其它语⾔的⼀个⼦程序，例如fft。

语句简单，内涵丰富。

同⼀个函数有不同的输⼊变量和输出变量，分别代表不同的含义。

Matlab既具有结构化的控制语句（if、for、while）⼜⽀持⾯向对象的程序设计。

⽅便的绘图功能。

包含功能强劲的⼯具箱。

易于扩展。

1.1.4 初识MATLAB例1-1 绘制正弦曲线和余弦曲线。

x=[0:0.5:360]*pi/180;plot(x,sin(x),x,cos(x));例1-2 求⽅程3x4+7x3+9x2-23=0的全部根。

p=[3,7,9,0,-23]; %建⽴多项式系数向量x=roots(p) %求根例1-3 求积分quad('x.*log(1+x)',0,1)例1-4 求解线性⽅程组。

a=[2,-3,1;8,3,2;45,1,-9];b=[4;2;17];x=inv(a)*b1.2 MATLAB的运⾏环境与安装1.2.1 MATLAB的运⾏环境硬件环境：(1) CPU(2) 内存(3) 硬盘(4) CD-ROM驱动器和⿏标软件环境：(1) Windows 98/NT/2000 或Windows XP(2) 其他软件根据需要选⽤1.2.2 MATLAB的安装运⾏系统的安装程序setup.exe，可以按照安装提⽰依次操作。

基于云模型效能评估的Matlab实现王旭辉;杨华;陈远【摘要】对基于云模型的系统效能评估方法及过程进行了简要的描述,用Matlab 代码实现了部分算法,代码经测试均可正确运行。

对云模型的研究和应用有一定的推广价值和研究意义。

%This paper describes the methods and processes for the system effectiveness evaluation based on cloud model,using Matlab to achieve part of the algorithm.Code in the text can be properly tested.And it has extension and research significance in the study and application of the cloud model.【期刊名称】《微型机与应用》【年(卷),期】2012(031)008【总页数】4页(P71-73,76)【关键词】Matlab;云模型;效能评估【作者】王旭辉;杨华;陈远【作者单位】重庆通信学院,重庆400035;重庆通信学院,重庆400035;重庆通信学院,重庆400035【正文语种】中文【中图分类】TP311.5对于一些复杂的系统，由于其不确定性即模糊性和随机性，很难准确地对其进行有效的效能评估。

因此需要一种评估方法，能够充分考虑到评估过程中出现的模型，同时能够有效而简便地实现定性与定量相互转换[1]。

云模型是由李德毅院士提出的一种定性定量互换模型，可将模糊性和随机性结合在一起，充分实现精确数值与定性语言之间的转换，可以有效地实现系统效能评估。

而Matlab既是一种直观、高效的计算机语言，同时又是一个科学计算平台。

它为数据分析和数据可视化、算法和应用程序开发提供了可靠的数学运算和高级图形绘制工具[2]。

第一讲：图论模型程序一：可达矩阵算法%根据邻接矩阵A〔有向图〕求可达矩阵P〔有向图〕function P=dgraf<A>n=size<A,1>;P=A;for i=2:nP=P+A^i;endP<P~=0>=1; %将不为0的元素变为1P;程序二：无向图关联矩阵和邻接矩阵互换算法F表示所给出的图的相应矩阵W表示程序运行结束后的结果f=0表示把邻接矩阵转换为关联矩阵f=1表示把关联矩阵转换为邻接矩阵%无向图的关联矩阵和邻接矩阵的相互转换function W=incandadf<F,f>if f==0 %邻接矩阵转换为关联矩阵m=sum<sum<F>>/2; %计算图的边数n=size<F,1>;W=zeros<n,m>;k=1;for i=1:nfor j=i:nif F<i,j>~=0W<i,k>=1; %给边的始点赋值为1W<j,k>=1; %给边的终点赋值为1k=k+1;endendendelseif f==1 %关联矩阵转换为邻接矩阵m=size<F,2>;n=size<F,1>;W=zeros<n,n>;for i=1:ma=find<F<:,i>~=0>;W<a<1>,a<2>>=1; %存在边,则邻接矩阵的对应值为1 W<a<2>,a<1>>=1;endelsefprint<'Please imput the right value of f'>;W;程序三：有向图关联矩阵和邻接矩阵互换算法%有向图的关联矩阵和邻接矩阵的转换function W=mattransf<F,f>if f==0 %邻接矩阵转换为关联矩阵m=sum<sum<F>>;n=size<F,1>;W=zeros<n,m>;k=1;for i=1:nfor j=i:nif F<i,j>~=0 %由i发出的边,有向边的始点W<i,k>=1; %关联矩阵始点值为1W<j,k>=-1; %关联矩阵终点值为-1k=k+1;endendendelseif f==1 %关联矩阵转换为邻接矩阵m=size<F,2>;n=size<F,1>;W=zeros<n,n>;for i=1:ma=find<F<:,i>~=0>; %有向边的两个顶点if F<a<1>,i>==1W<a<1>,a<2>>=1; %有向边由a<1>指向a<2>elseW<a<2>,a<1>>=1; %有向边由a<2>指向a<1>endendelsefprint<'Please imput the right value of f'>;endW;第二讲：最短路问题程序0：最短距离矩阵W表示图的权值矩阵D表示图的最短距离矩阵%连通图中各项顶点间最短距离的计算function D=shortdf<W>%对于W<i,j>,若两顶点间存在弧,则为弧的权值,否则为inf；当i=j时W<i,j>=0 n=length<W>;m=1;while m<=nfor i=1:nfor j=1:nif D<i,j>>D<i,m>+D<m,j>D<i,j>+D<i,m>+D<m,j>; %距离进行更新 endendendm=m+1;endD;程序一：Dijkstra算法〔计算两点间的最短路〕function [l,z]=Dijkstra<W>n = size <W,1>;for i = 1 :nl<i>=W<1,i>;z<i>=0;endi=1;while i<=nfor j =1 :nif l<i>>l<j>+W<j,i>l<i>=l<j>+W<j,i>;z<i>=j-1;if j<ii=j-1;endendendi=i+1;end程序二：floyd算法〔计算任意两点间的最短距离〕function [d,r]=floyd<a>n=size<a,1>;d=a;for i=1:nfor j=1:nr<i,j>=j;endendr;for k=1:nfor i=1:nfor j=1:nif d<i,k>+d<k,j><d<i,j>d<i,j>=d<i,k>+d<k,j>; r<i,j>=r<i,k>;endendendend程序三：n2short.m 计算指定两点间的最短距离function [P u]=n2short<W,k1,k2>n=length<W>;U=W;m=1;while m<=nfor i=1:nfor j=1:nif U<i,j>>U<i,m>+U<m,j>U<i,j>=U<i,m>+U<m,j>;endendendm=m+1;endu=U<k1,k2>;P1=zeros<1,n>;k=1;P1<k>=k2;V=ones<1,n>*inf;kk=k2;while kk~=k1for i=1:nV<1,i>=U<k1,kk>-W<i,kk>;if V<1,i>==U<k1,i>P1<k+1>=i;kk=i;k=k+1;endendendk=1;wrow=find<P1~=0>;for j=length<wrow>:-1:1P<k>=P1<wrow<j>>;k=k+1;endP;程序四、n1short.m<计算某点到其它所有点的最短距离> function[Pm D]=n1short<W,k>n=size<W,1>;D=zeros<1,n>;for i=1:n[P d]=n2short<W,k,i>;Pm{i}=P;D<i>=d;end程序五：pass2short.m<计算经过某两点的最短距离> function [P d]=pass2short<W,k1,k2,t1,t2>[p1 d1]=n2short<W,k1,t1>;[p2 d2]=n2short<W,t1,t2>;[p3 d3]=n2short<W,t2,k2>;dt1=d1+d2+d3;[p4 d4]=n2short<W,k1,t2>;[p5 d5]=n2short<W,t2,t1>;[p6 d6]=n2short<W,t1,k2>;dt2=d4+d5+d6;if dt1<dt2d=dt1;P=[p1 p2<2:length<p2>> p3<2:length<p3>>]; elsed=dt1;p=[p4 p5<2:length<p5>> p6<2:length<p6>>]; endP;d;第三讲：最小生成树程序一：最小生成树的Kruskal算法function [T c]=krusf<d,flag>if nargin==1n=size<d,2>;m=sum<sum<d~=0>>/2;b=zeros<3,m>;k=1;for i=1:nfor j=<i+1>:nif d<i,j>~=0b<1,k>=i;b<2,k>=j;b<3,k>=d<i,j>;k=k+1;endendendelseb=d;endn=max<max<b<1:2,:>>>;m=size<b,2>;[B,i]=sortrows<b',3>;B=B';c=0;T=[];k=1;t=1:n;for i=1:mif t<B<1,i>>~=t<B<2,i>>T<1:2,k>=B<1:2,i>;c=c+B<3,i>;k=k+1;tmin=min<t<B<1,i>>,t<B<2,i>>>; tmax=max<t<B<1,i>>,t<B<2,i>>>; for j=1:nif t<j>==tmaxt<j>=tmin;endendendif k==nbreak;endendT;c;程序二：最小生成树的Prim算法function [T c]=Primf<a>l=length<a>;a<a==0>=inf;k=1:l;listV<k>=0;listV<1>=1;e=1;while <e<l>min=inf;for i=1:lif listV<i>==1for j=1:lif listV<j>==0 & min>a<i,j>min=a<i,j>;b=a<i,j>;s=i;d=j;endendendendlistV<d>=1;distance<e>=b;source<e>=s;destination<e>=d;e=e+1;endT=[source;destination];for g=1:e-1c<g>=a<T<1,g>,T<2,g>>;endc;第四讲：Euler图和Hamilton图程序一：Fleury算法〔在一个Euler图中找出Euler环游〕注：包括三个文件；fleuf1.m, edf.m, flecvexf.mfunction [T c]=fleuf1<d>%注：必须保证是Euler环游,否则输出T=0,c=0n=length<d>;b=d;b<b==inf>=0;b<b~=0>=1;m=0;a=sum<b>;eds=sum<a>/2;ed=zeros<2,eds>;vexs=zeros<1,eds+1>;matr=b;for i=1:nif mod<a<i>,2>==1m=m+1;endendif m~=0fprintf<'there is not exit Euler path.\n'>T=0;c=0;endif m==0vet=1;flag=0;t1=find<matr<vet,:>==1>;for ii=1:length<t1>ed<:,1>=[vet,t1<ii>];vexs<1,1>=vet;vexs<1,2>=t1<ii>;matr<vexs<1,2>,vexs<1,1>>=0;flagg=1;tem=1;while flagg[flagg ed]=edf<matr,eds,vexs,ed,tem>;tem=tem+1;if ed<1,eds>~=0 & ed<2,eds>~=0T=ed;T<2,eds>=1;c=0;for g=1:edsc=c+d<T<1,g>,T<2,g>>;endflagg=0;break;endendendendfunction[flag ed]=edf<matr,eds,vexs,ed,tem>flag=1;for i=2:eds[dvex f]=flecvexf<matr,i,vexs,eds,ed,tem>;if f==1flag=0;break;endif dvex~=0ed<:,i>=[vexs<1,i> dvex];vexs<1,i+1>=dvex;matr<vexs<1,i+1>,vexs<1,i>>=0;elsebreak;endendfunction [dvex f]=flecvexf<matr,i,vexs,eds,ed,temp> f=0;edd=find<matr<vexs<1,i>,:>==1>;dvex=0;dvex1=[];ded=[];if length<edd>==1dvex=edd;elsedd=1;dd1=0;kkk=0;for kk=1:length<edd>m1=find<vexs==edd<kk>>;if sum<m1>==0dvex1<dd>=edd<kk>;dd=dd+1;dd1=1;elsekkk=kkk+1;endendif kkk==length<edd>tem=vexs<1,i>*ones<1,kkk>;edd1=[tem;edd];for l1=1:kkklt=0;ddd=1;for l2=1:edsif edd1<1:2,l1>==ed<1:2,l2>lt=lt+1;endendif lt==0ded<ddd>=edd<l1>;ddd=ddd+1;endendendif temp<=length<dvex1>dvex=dvex1<temp>;elseif temp>length<dvex1> & temp<=length<ded>dvex=ded<temp>;elsef=1;endend程序二：Hamilton改良圈算法〔找出比较好的Hamilton路〕function [C d1]= hamiltonglf<v>%d表示权值矩阵%C表示算法最终找到的Hamilton圈.%v =[ 51 67;37 84;41 94;2 99;18 54;4 50;24 42;25 38;13 40;7 64;22 60;25 62;18 40;41 26];n=size<v,1>;subplot<1,2,1>hold on;plot <v<:,1>,v<:,2>,'*'>; %描点for i=1:nstr1='V';str2=num2str<i>;dot=[str1,str2];text<v<i,1>-1,v<i,2>-2,dot>; %给点命名endplot <v<:,1>,v<:,2>>;%连线plot<[v<n,1>,v<1,1>],[v<n,2>,v<1,2>]>;for i =1:nfor j=1:nd<i,j>=sqrt<<v<i,1>-v<j,1>>^2+<v<i,2>-v<j,2>>^2>;endendd2=0;for i=1:nif i<nd2=d2+d<i,i+1>;elsed2=d2+d<n,1>;endendtext<10,30,num2str<d2>>;n=size<d,2>;C=[linspace<1,n,n> 1];for nnn=1:20C1=C;if n>3for m=4:n+1for i=1:<m-3>for j=<i+2>:<m-1>if<d<C<i>,C<j>>+d<C<i+1>,C<j+1>><d<C<i>,C<i+1>>+d<C<j>,C<j+1>>>C1<1:i>=C<1:i>;for k=<i+1>:jC1<k>=C<j+i+1-k>;endC1<<j+1>:m>=C<<j+1>:m>;endendendendelseif n<=3if n<=2fprint<'It does not exist Hamilton circle.'>; elsefprint<'Any cirlce is the right answer.'>;endendC=C1;d1=0;for i=1:nd1=d1+d<C<i>,C<i+1>>;endd1;endsubplot<1,2,2>;hold on;plot <v<:,1>,v<:,2>,'*'>; %描点for i=1:nstr1='V';str2=num2str<i>;dot=[str1,str2];text<v<i,1>-1,v<i,2>-2,dot>; %给点命名endv2=[v;v<1,1>,v<1,2>];plot<v<C<:>,1>,v<C<:>,2>,'r'>;text<10,30,num2str<d1>>;第五讲：匹配问题与算法程序一：较大基础匹配算法function J=matgraf<W>n=size<W,1>;J=zeros<n,n>;while sum<sum<W>>~=0a=find<W~=0>;t1=mod<a<1>,n>;if t1==0t1=n;endif a<1>/n>floor<a<1>/n>t2=floor<a<1>/n>+1;elset2=floor<a<1>/n>;endJ<t1,t2>=1,J<t2,t1>=1;W<t1,:>=0;W<t2,:>=0;W<:,t1>=0;W<:,t2>=0;endJ;程序二：匈牙利算法〔完美匹配算法,包括三个文件fc01,fc02,fc03〕function [e,s]=fc01<a,flag>if nargin==1flag=0;endb=a;if flag==0cmax=max<max<b>'>;b=cmax-b;endm=size<b>;for i =1:m<1>b<i,:>=b<i,:>-min<b<i,:>>;endfor j=1:m<2>b<:,j>=b<:,j>-min<b<:,j>>;endd=<b==0>;[e,total]=fc02<d>;while total~=m<1>b=fc03<b,e>;d=<b==0>;[e,total]=fc02<d>;endinx=sub2ind<size<a>,e<:,1>,e<:,2>>;e=[e,a<inx>];s=sum<a<inx>>;function [e,total]=fc02<d>total=0;m=size<d>;e=zeros<m<1>,2>;t=sum<sum<d>'>;nump=sum<d'>;while t~=0[s,inp]=sort<nump>;inq=find<s>;ep=inp<inq<1>>;inp=find<d<ep,:>>;numq=sum<d<:,inp>>;[s,inq]=sort<numq>;eq=inp<inq<1>>;total=total+1;e<total,:>=[ep,eq];inp=find<d<:,eq>>;nump<inp>=nump<inp>-1;nump<ep>=0;t=t-sum<d<ep,:>>-sum<d<:,eq>>+1;d<ep,:>=0*d<ep,:>;d<:,eq>=0*d<:,eq>;endfunction b=fc03<b,e>m=size<b>;t=1;p=ones<m<1>,1>;q=zeros<m<1>,1>;inp=find<e<:,1>~=0>;p<e<inp,1>>=0;while t~=0tp=sum<p+q>;inp=find<p==1>;n=size<inp>;for i=1:n<1>inq=find<b<inp<i>,:>==0>;q<inq>=1;endinp=find<q==1>;n=size<inp>;for i=1:n<1>if all<e<:,2>-inp<i>>==0inq=find<<e<:,2>-inp<i>>==0>;p<e<inq>>=1;endendtq=sum<p+q>;t=tq-tp;endinp=find<p==1>;inq=find<q==0>;cmin=min<min<b<inp,inq>>'>;inq=find<q==1>;b<inp,:>=b<inp,:>-cmin;b<:,inq>=b<:,inq>+cmin;第六讲：最大流最小费用问题程序一：2F算法<Ford-Fulkerson算法>,求最大流%C=[0 5 4 3 0 0 0 0;0 0 0 0 5 3 0 0;0 0 0 0 0 3 2 0;0 0 0 0 0 0 2 0; %0 0 0 0 0 0 0 4;0 0 0 0 0 0 0 3;0 0 0 0 0 0 0 5;0 0 0 0 0 0 0 0 ] function [f wf]=fulkersonf<C,f1>%C表示容量%f1表示当前流量,默认为0%f表示最大流±íʾ×î´óÁ÷%wf表示最大流的流量n=length<C>;if nargin==1;f=zeros<n,n>;elsef=f1;endNo=zeros<1,n>;d=zeros<1,n>;while <1>No<1>=n+1;d<1>=Inf;while <1>pd=1;for <i=1:n>if <No<i>>for <j=1:n>if <No<j>==0 & f<i,j><C<i,j>>No<j>=i;d<j>=C<i,j>-f<i,j>;pd=0;if <d<j>>d<i>>d<j>=d<i>;endelseif <No<j>==0 & f<j,i>>0>No<j>=-i;d<j>=f<j,i>;pd=0;if <d<j>>d<i>>d<j>=d<i>;endendendendendif <No<n>|pd>break;endendif <pd>break;enddvt=d<n>;t=n;while <1>if<No<t>>0>f<No<t>,t>=f<No<t>,t>+dvt;elseif <No<t><0>f<No<t>,t>=f<No<t>,t>-dvt;endif <No<t>==1>for <i=1:n>No<i>=0;d<i>=0;endbreakendt=No<t>;endendwf=0;for <j=1:n>wf=wf+f<1,j>;endf;wf;程序二：Busacker-Gowan算法<求最大流最小费用>%C=[0 15 16 0 0;0 0 0 13 14;0 11 0 17 0;0 0 0 0 8;0 0 0 0 0] %b=[0 4 1 0 0;0 0 0 6 1;0 2 0 3 0;0 0 0 0 2;0 0 0 0 0]%function [f wf zwf]=BGf<C,b>%C表示弧容量矩阵%b表示弧上单位流量的费用%f表示最大流最小费用矩阵%wf最大流量%zwf表示最小费用n=size<C,2>;wf=0;wf0=inf;f=zeros<n,n>;while <1>a=ones<n,n>*inf;for <i=1:n>a<i,i>=0;endfor <i=1:n>for <j=1:n>if<C<i,j>>0 & f<i,j>==0>a<i,j>=b<i,j>;elseif <C<i,j>>0 & f<i,j>==C<i,j>>a<j,i>=-b<i,j>;elseif <C<i,j>>0>a<i,j>=b<i,j>;a<j,i>=-b<i,j>;endendendfor <i=2:n>p<i>=inf;s<i>=i;endfor <k=1:n>pd=1;for <i=2:n>for <j=1:n>if <p<i>>p<j>+a<j,i>>p<i>=p<j>+a<j,i>;s<i>=j;pd=0; endendendif <pd>break;endendif <p<n>==inf>break;enddvt=inf;t=n;while <1>if <a<s<t>,t>>0>dvtt=C<s<t>,t>-f<s<t>,t>;elseif <a<s<t>,t><0>dvtt=f<t,s<t>>;endif <dvt>dvtt>dvt=dvtt;endif <s<t>==1>break;endt=s<t>;endpd=0;if <wf+dvt>=wf0>dvt=wf0-wf;pd=1;endt=n;while <1>if <a<s<t>,t>>0>f<s<t>,t>=f<s<t>,t>+dvt; elseif <a<s<t>,t><0>f<<t>,s<t>>=f<t,s<t>>-dvt; endif <s<t>==1>break;endt=s<t>;endif <pd>break;endwf=0;for <j=1:n>wf=wf+f<1,j>;endendzwf=0;for <i=1:n>for <j=1:n>zwf=zwf+b<i,j>*f<i,j>;endendf;。

01 MATLABChapterMATLAB简介MATLAB是一种高级编程语言和环境，主要用于数值计算、数据分析、信号处理、图像处理等多种应用领域。

MATLAB具有简单易学、高效灵活、可视化强等特点，被广泛应用于科研、工程、教育等领域。

MATLAB提供了丰富的函数库和工具箱，方便用户进行各种复杂的数学计算和数据分析。

MATLAB安装与启动MATLAB界面介绍工作空间用于显示当前定义的所有变量及其值。

命令历史记录了用户输入过的命令及其输出结果。

基本运算与数据类型02矩阵运算与数组操作Chapter01020304使用`[]`或`zeros`、`ones`等函数创建矩阵创建矩阵使用`size`函数获取矩阵大小矩阵大小通过下标访问矩阵元素，如`A(i,j)`矩阵元素访问使用`disp`或`fprintf`函数显示矩阵信息矩阵信息矩阵创建与基本操作对应元素相加，如`C = A+ B`加法运算矩阵运算对应元素相减，如`C = A-B`减法运算数与矩阵相乘，如`B = k *A`数乘运算使用单引号`'`进行转置，如`B = A'`转置运算满足乘法条件的矩阵相乘，如`C = A * B`矩阵乘法使用`inv`函数求逆矩阵，如`B = inv(A)`逆矩阵数组创建数组大小数组元素访问数组操作数组操作01020304线性方程组求解数据处理与分析特征值与特征向量图像处理矩阵与数组应用实例03数值计算与数据分析Chapter数值计算基础MATLAB基本运算数值类型与精度变量与表达式函数与脚本数据分析方法数据导入与预处理学习如何导入各种格式的数据（如Excel、CSV、TXT等），并进行数据清洗、转换等预处理操作。

数据统计描述掌握MATLAB中数据统计描述的方法，如计算均值、中位数、标准差等统计量，以及绘制直方图、箱线图等统计图表。

数据相关性分析学习如何在MATLAB中进行数据相关性分析，如计算相关系数、绘制散点图等。

Matlab实现GM（1,1）模型（源代码）关于这个模型的介绍不想多说了，只是⼀个娱乐⽽已。

下⾯是所有的代码，直接粘到你的M⽂件⾥⾯，然后跑就是了。

⼀分钱不收。

function [ simulation,params] = GM( org )n=length(org);%⼀次累加for i=1:nacc(i)=sum(org(1:i));end%计算背景值for i=1:(n-1)zk(i)=0.5*(acc(i)+acc(i+1));end%求解参数params=polyfit(zk,org(2:end),1);%计算模拟值for i=1:nif i==1simulation(i)=org(1);elsesimulation(i)=(org(1)+params(2)/params(1))*(1-exp(-params(1)))*exp(params(1)*(i-1));endendplot(1:n,org,'-o',1:n,simulation,'-*');legend('原始序列','拟合序列');细⼼的朋友应该会注意到⼀件事情：灰⾊预测模型⾥⾯不是有那么多矩阵运算吗，在这⾥怎么没有？如果你跑了程序⼜会发现，这个程序计算出来的结果，跟任何⼀本书上写的结果完全⼀样。

这是为啥嘞？如果再细⼼点，会看到我这⾥获取参数的代码： params=polyfit(zk,org(2:end),1);。

没错，就是线性拟合。

任何⼀本讲灰⾊理论的书上都会告诉你，参数估计是由这个式⼦加上最⼩⼆乘法得到的。

这事情的确没有错，但如果你仔细点，把移到等式的右边去，你发现了什么。

没错，这TM不就是⼀个离散直线⽅程么。

那么这⾥只需要把看成是直线⽅程⾥的y,⽽把看成是x。

那这个参数估计，就只是个简单的线性回归⽽已。

这样⼀来，只要是能实现线性回归的函数，完全都可以实现它所谓的参数估计。

1.绘制云图Ex=18En=2He=0。

2hold onfor i=1:1000Enn=randn（1）*He+En;x（i）=randn（1）*Enn+Ex;y（i）=exp(—（x（i）—Ex)^2/（2＊Enn^2)); plot（x(i),y（i)，'＊')endEx=48.7En=9。

1He=0。

39hold onfor i=1：1000Enn=randn(1)＊He+En；x（i)=randn(1)*Enn+Ex;y(i)=exp（—（x(i）—Ex)^2/（2*Enn^2））；plot（x（i)，y(i),'＊')end2.求期望、熵及超熵X1=[51。

93 52。

51 54。

70 43.14 43。

85 44.48 44。

61 52.08]；Y1=［0.91169241573 0。

921875 0。

96032303371 0.75737359551 0.76983848315 0。

7808988764 0.78318117978 0.9143258427]；m=8；Ex=mean（X1)En1=zeros(1，m）;for i=1:mEn1（1，i）=abs(X1（1,i）—Ex)/sqrt（-2＊log(Y1（1，i）））;endEn=mean(En1);He=0;for i=1:mHe=He+(En1(1,i)—En)^2;endEn=mean(En1)He=sqrt（He/(m—1）)3。

平顶山so2环境：X1=[0。

013 0。

04 0。

054 0。

065 0。

07 0.067 0.058 0。

055 0.045］；Y1=［0。

175675676 0。

540540541 0.72972973 0.878378378 0.945945946 0.905405405 0。

783783784 0。

743243243 0。

608108108］；m=9;Ex=mean（X1）En1=zeros（1，m);for i=1：mEn1(1,i）=abs(X1（1,i）—Ex）/sqrt（-2*log(Y1(1,i）））；endEn=mean(En1）；He=0；for i=1：mHe=He+(En1(1,i)-En)^2；endEn=mean（En1)He=sqrt(He/(m-1))1。

一维云模型 程序： clc clearEx=170;En=5;He=0.5;n=5000;for i=l:nEnn=randn( 1 )*He+En;x(i)=randn(l )*Enn+Ex;y ⑴=exp(-(x(i)-Ex)A 2/(2*Enn A 2));endplot(x,y ；.r ,)title('5000个男生身高的一维云图) ylabef 确定度)；xlabelC 身高值，);axis([ 150」9001])grid on一维：clear vars;clc;close all;Exl 二-8; Enl 二0・ 7; Hel=0. 2;nl 二200; Ex2二2.2; En2=2;He2=0. 5; n2=800; Ex3=18; En3=4; He3=0. 7; n3=1500;Enl_t = normrnd(Enl, Hel, nl, 1);datal = normrnd(Exl, Enl t, nl, 1);150 6 5 4 3 2 1 O1 o.o.o.o.o.o.93 X — 5 8 di如T — 75 1—拓 17亠咼 身65 di 60 4— 5 5 1 5000个男主身高的一維云图9 B 7 o.o.o.mul = exp(-0. 5*((datal-Exl). /Enl_t). 2);En2_t = normrnd (En2, He2, n2, 1);data2 = normrnd (Ex2, En2_t, n2,1);mu2 = exp(-0. 5*((data2-Ex2). /En2_t)・ ~2);En3_t = normrnd (En3, He3, n3, 1);data3 = normrnd(Ex3, En3_t, n3,1);mu3 = exp(-0. 5*((data3-Ex3). /En3_t). 2);figure(l);plot (data!, mul, I b‘，data2, mu2,' *r‘, data3, mu3,' +k'); axis equal;二维云模型程序：clcclearEx l = 170;Enl=5;He 1=0.5;Ex2=65 ;En2=3 ;He2=0.2; n=5000;for i=I:nEnn 1 =randn( 1 )*He 1 +En 1; x l(i)=randn( 1 )*Enn 1 +Ex 1;Enn2=randn( 1 )*He2+En2; x2(i)=randn( 1 )*Enn2+Ex2;y(i)=exp(-(x 1 (i)-Ex 1 )A2/(2*Enn 1 A2)-(x2(i)-Ex2)A2/(2*Enn2A2)); end plot3(xl,x2,y,'f)title('5OOO个男生身高体jg的二维云图')axis([ 148,190.50,80 A I])grid on结果：5ooyi-男生身高体重的二维云图50 160多个一维clear vars;clc;close all;Exl二0; Enl=0.103; Hel二0.013; nl=5000;Ex2二0.309; En2=0.064; He2=0.008; n2=5000;Ex3二0・ 5; En3二0・ 039; He3=0. 005; n3=5000;Ex4=0.691; En4=0.064; He4=0.008; n4=5000;Ex5=l; En5二0.103; He5=0.013; n5=5000:Enl_t = normrnd(Enl, Hel, nl, 1);datal = normrnd(Exl, Enl_t, nl,1);mul = exp(-0. 5*((datal-Exl). /Enl_t). 2);En2_t = normrnd (En2, He2, n2, 1);data2 = normrnd(Ex2, En2_t, n2, 1);mu2 = exp(-0. 5*((data2-Ex2). /En2_t). *2);En3_t = normrnd (En3, He3, n3, 1);data3 = normrnd(Ex3, En3_t, n3,1);mu3 = exp(-0. 5*((data3-Ex3). /En3_t). 2);En4_t = normrnd(En4, He4, n4, 1);data4 = normrnd(Ex4, En4_t, n4,1);mu4 = exp(-0. 5*((data4-Ex4)・/En4_t)・ 2);En5_t = normrnd (En5, He5, n5, 1);data5 = normrnd (Ex5, En5_t, n5, 1);mu5 = exp (一0・ 5* ((data5-Ex5)・/En5_t)・2);figure(l);plot (datal, mul,'・ r*, data2, mu2,'・r , data3, mu3,'・r , data4, mu4,'・ r*, data5, mu5,'・ r* ); titleC评价集')ylabelC 隶属度');axis([-0. 4, 1. 4, 0, 1])grid on评价集04 02 0 0.2 0.4 0.6 0.8 1 1.2 1.4一维Ex二1100;En二84. 926;He 二0. 1;n二1000;X=zeros (1, n);Y=zeros (1, n);X(1 :n) =normrnd(En, He, 1, n):for i=l:nEnl二X(l, i);X(l, i)=normrnd(Ex, Enl, 1):Y(l, i)=exp((-(X(l, i)-Ex)"2)/(2*En「2));plot(X, Y,'. ',' MarkerEdgeCo1or，‘ k', ' markersize*, 4); title C强等级','fontsize', 16);grid on;end强等级逆发生器代码X1=X;Y1=Y;i=l；while i<=(n-flag)lfYl(l,i)>0.9999Y1(：J)=[]；Xl(：,i)=[]；flag=flag+l;End;Ex=mean(Xl);En2=zeros⑴m);for i=l:m;Enl(lJ)=abs(Xl(l/i).Ex)/sqrt(.2*log(Yl(l/i))); End;En二mean(Enl);He=O;for i=l:m;He=He+(Enl(lJ)-En)A2;He=sqrt(He/(m-l));End;XI =X;Y1=Y;i=l；while i<=(n-flag)ifYl(lj)>0.9999Y1(：J)=[J；X1(：J)=[]；flag=flag+l;elsei=i+l;m=m +1;endendEx=mean(Xl)En l=zeros(l z m);for i= l:mEnl(l,i)=abs(Xl(l/i)-Ex)/sqrt(-2*log(Yl(l/i))); endEn二mea n(Enl);He=0;for i=l:mHe=He+(Enl(l /i)-En)A 2; endHe=sqrt(He/(m-l))Enl_t = normrnd(Enl, Hel, nl, 1); datal = normrnd(Exl, Enl_t, nl, 1); mul = exp(-0. 5*((datal-Exl). /Enl_t). 2);En2_t = normrnd (En2, He2, n2, 1);data2 = normrnd(Ex2, En2_t, n2, 1);mu2 = exp(-0. 5*((data2-Ex2). /En2_t). *2);En3_t = normrnd (En3, He3, n3, 1);data3 = normrnd(Ex3, En3_t, n3,1);mu3 = exp(-0. 5*((data3-Ex3)・/En3_t). 2);En4_t = normrnd(En4, He4, n4, 1);data4 = normrnd (Ex4, En4_t, n4, 1); mu4 = exp(-0. 5*((data4-Ex4). /En4_t)・~2); En5_t = normrnd (En5, He5, n5, 1);data5 = normrnd(Ex5, En5_t, n5,1);mu5 = exp (一0・ 5*((data5~Ex5)・/En5_t)・ 2);En6_t = normrnd (En6, He6, n6, 1);data6 = normrnd(Ex6, En6_t, n6,1);mu6 = exp(-0. 5*((data6-Ex6)・/En6_t). 2);En7_t = normrnd (En7, He7, n7, 1);data? = normrnd (Ex7, En7_t, n7, 1);mu7 = exp(-0. 5*((data7-Ex7). /En7_t)・ ~2);En8_t = normrnd (En8, He8, n8, 1); dataS = normrnd (Ex8, En8_t, n& 1);clear vars;clc;close all;Enl 二0.150; Hel=0. 050; Exl=0. 457; Ex2二0・454; Ex3二0・435; Ex4二0. 415; Ex5=0. 414; Ex6 二0.410;Ex7 二0.410; Ex8=0. 500;En2=0. 156 En3=0. 229 En4=0. 177 En5=0. 298 En6=0. 242 En7=0. 188 En8=0. 039 He2=0. 056 He3=0. 067 He4=0. 071 He5=0. 099 He6=0.061 He7=0.061 He8=0.005 nl=4000; n2=4000;n3=4000;n4=4000;n5=4000;n6=4000;n7=4000;n8=5000;mu8 = exp(-0. 5*((data8-Ex8). /En8_t). *2);figure(l);plot (datal, mul,'・ r*, data2, mu2,'・ r , data3, mu3,'・ r , data4, mu4,'・ r*, data5, mu5,'・ r* ,data6, mu6,'・:r' , data7, mu7,'・ r*, data8, mu8,'・ r ):titleC 评价集')ylabel ('隶属度');axis([-0. 4, 1. 4, 0, 1])grid onclear vars;clc;close all;Enl_t = normrnd(Enl, Hel, nl, 1); datal = normrnd(Exl, Enl_t, nl, 1); mul = exp(-0. 5*((datal-Exl). /Enl_t). 2);En2_t = normrnd (En2, He2, n2, 1);data2 = normrnd (Ex2, En2_t, n2,1); mu2 = exp(-0. 5*((data2-Ex2). /En2_t)・ 2);En3_t = normrnd (En3, He3, n3, 1);data3 = normrnd(Ex3, En3_t, n3,1); mu3 = exp (-0. 5* ((data3-Ex3). /En3_t). 2);En4_t = normrnd(En4, He4, n4, 1);data4 = normrnd (Ex4, En4_t, n4, 1); mu4 = exp(-0. 5*((data4-Ex4). /En4_t)・ ~2);En5_t = normrnd (En5, He5, n5, 1);data5 = normrnd (Ex5, En5_t, n5, 1);mu5 = exp (一0. 5* ((data5-Ex5)・/En5_t)・ 2);figure(l);plot (datal, mul,'・ r , data2, mu2,'・ r , data3, mu3,'・ x , data4, mu4,'・, data5, mu5,'・ r* );titleC 评价集')ylabel(，隶属度');axis([-0. 4, 1. 4, 0, 1])grid on Exl 二0.716;Ex2=0. 545;Ex3二0・534; Ex4二0.Enl 二0.123; Hel=0. 045; nl=4000; En2=0. 140; He2=0. 052 En3=0. 233; He3=0. 085 En 仁0.202; He4=0. 063 En5=0. 064; n2=4000; n3=4000; n4=4000; He5=0. 008; n5二6000;。

Matlab编程和模拟模型1.编程训练题目一.有一个向量V二ai,a2, ,a n，编程求解下列式子:n2i Js =送a ii -12 i 2 | , 2S2 =a i • a3 "…”au其中u为不超过n的最大奇数。

自己给出测试例子，并给出运算结果二•模拟一次扑克牌洗牌过程，输出牌的顺序%4*13+2paihao二[11:23,31:43,51:63,71:83,98,99];if len gth(paihao)~=54, error('error in nu mbe门end PAIXU二ra ndperm(54);fapai = paihao(PAIXU)三.模拟1000次投币过程，输出出现正面的频率。

程序1:nu m_zhe ng=0;for i=1:1000,cur=ra nd;if cur<0.5,nu m_zhe ng二nu m_zhe ng + 1; endendf = num_zhe ng/1000四•问题：现有一个文本文件（mydata・txt）,包含了火车的出发和到达时刻，基本格式如下（实际中该文件超过1000行）19:35 07:47 19:14 07:12 19:21 07:19 18:53 08:2319:07 07:05 19:00 06:58 21:37 08:04 20:40 07:4021:44 07:22 21:30 07:25 19:28 06:48 22:00 07:1019:21 07:19 18:53 08:23 19:07 07:050:00 时刻记为初要求把时间读取并存为矩阵数据，并且需要将其以始时刻，把奇数行数据转为分钟。

准备知识：（1）文件打开（fopen），关闭（fclose）;（2）读取各行数据（fgetl）（3）解析各行数据，并转换数据注：处理方法不唯一。

文本文件：fopen，fclose，fgetl。

%先初始化矩阵mat=[];row = 0;fid=fopen('mydata.txt');while 1tline = fgetl(fid);if feof(fid), break, end disp(tline)cur=str2num(tline); row = row + 1;% 将当前行的(行)向量保存到mat 中if isempty(mat), mat二cur;elselen=len gth(cur); mat(row,1:le n)二cur; end end fclose(fid);19 35 7 47 8 31 9 4219 14 7 12 0 0 0 019 21 7 19 0 0 0 018 53 8 23 0 0 0 019 7 7 5 0 0 0 019 0 6 58 0 0 0 021 37 8 4 0 0 0 020 40 7 40 0 0 0 021 44 7 22 0 0 0 021 30 7 25 0 0 0 019 28 6 48 0 0 0 0五.（适中）有一个文件mytest・txt,内容如下:特点：第2行开始为数值数据。