云模型简介及个人理解matlab程序文件

云模型粒子群matlab
云模型和粒子群优化算法都是计算机科学和工程领域中的重要概念。

云模型是一种描述不确定性、模糊性和复杂性的数学模型，它可以用来处理模糊信息和不确定性问题。

而粒子群优化算法是一种启发式优化算法，灵感来源于鸟群觅食的行为，通过模拟鸟群中个体的行为来寻找最优解。

在MATLAB中，你可以使用云模型和粒子群优化算法来解决各种问题。

对于云模型，MATLAB提供了模糊逻辑工具箱，可以用来建立和分析模糊系统，进行模糊推理和模糊控制等操作。

你可以使用MATLAB 中的模糊逻辑工具箱来创建云模型，并进行模糊推理和模糊控制。

对于粒子群优化算法，MATLAB也提供了相应的工具箱，比如Global Optimization Toolbox中的粒子群算法。

你可以使用MATLAB 中的粒子群算法来解决各种优化问题，比如函数优化、参数估计等。

如果你想结合云模型和粒子群优化算法，你可以先使用云模型处理模糊信息和不确定性，然后将处理过的信息输入到粒子群优化
算法中进行优化。

这样可以更好地处理复杂系统中的模糊和不确定性问题，并找到最优解。

总的来说，在MATLAB中结合云模型和粒子群优化算法可以帮助你解决各种复杂的模糊、不确定性和优化问题，为工程和科学领域的研究和实践提供有力的支持。

希望这个回答能够帮助到你。

云模型简介及个人理解m a t l a b程序集团档案编码：[YTTR-YTPT28-YTNTL98-UYTYNN08]随着不确定性研究的深入，越来越多的科学家相信，不确定性是这个世界的魅力所在，只有不确定性本身才是确定的。

在众多的不确定性中，和是最基本的。

针对和在处理不确定性方面的不足，1995年我国工程院院士教授在概率论和模糊数学的基础上提出了云的概念，并研究了模糊性和随机性及两者之间的关联性。

自李德毅院士等人提出云模型至今，云模型已成功的应用到、、、智能控制、等众多领域.设是一个普通集合。

, 称为论域。

关于论域中的模糊集合，是指对于任意元素都存在一个有稳定倾向的随机数，叫做对的隶属度。

如果论域中的元素是简单有序的，则可以看作是基础变量，隶属度在上的分布叫做隶属云；如果论域中的元素不是简单有序的，而根据某个法则，可将映射到另一个有序的论域上，中的一个且只有一个和对应，则为基础变量，隶属度在上的分布叫做隶属云[1] 。

数字特征云模型表示自然语言中的基元——语言值，用云的数字特征——期望Ex，熵En和超熵He表示语言值的数学性质[3] 。

期望 Ex：云滴在论域空间分布的期望，是最能够代表定性概念的点，是这个概念量化的最典型样本。

熵 En：“熵”这一概念最初是作为描述热力学的一个状态参量，此后又被引入统计物理学、信息论、复杂系统等，用以度量不确定的程度。

在云模型中，熵代表定性概念的可度量粒度，熵越大，通常概念越宏观，也是定性概念不确定性的度量，由概念的随机性和模糊性共同决定。

一方面, En是定性概念随机性的度量，反映了能够代表这个定性概念的云滴的离散程度；另一方面，又是定性概念亦此亦彼性的度量，反映了在论域空间可被概念接受的云滴的取值范围。

用同一个数字特征来反映随机性和模糊性，也必然反映他们之间的关联性。

超熵 He：熵的不确定性度量，即熵的熵，由熵的随机性和模糊性共同决定。

反映了每个数值隶属这个语言值程度的凝聚性，即云滴的凝聚程度。

Matlab仿真建模的基本原理与技术Matlab（Matrix Laboratory）是一种高级编程语言和环境，广泛应用于科学与工程领域。

它具备强大的数值计算和数据可视化功能，能够帮助工程师和科学家解决各种实际问题。

本文将探讨Matlab仿真建模的基本原理与技术。

一、Matlab的基本特点Matlab是一款强大的数学工具，具有以下特点：1. 矩阵运算能力：Matlab的核心功能是进行矩阵数学运算。

它提供了简洁而强大的语法，使得矩阵和向量的计算变得方便且高效。

2. 大量的内置函数：Matlab拥有丰富的内置函数库，包括数值计算、信号处理、图像处理、优化、统计等领域。

这些函数可以极大地简化复杂问题的求解过程。

3. 可视化功能：Matlab提供了丰富的数据可视化工具，能够直观地显示和分析数据。

用户可以通过绘制曲线、制作动画等方式，深入了解数据的规律。

4. 兼容性：Matlab是跨平台的，可以在多个操作系统上运行，如Windows、Linux和MacOS等。

这使得用户可以在不同的计算环境下无缝切换和共享代码。

5. 可扩展性：Matlab支持用户自定义函数和工具箱的开发。

这样，用户可以根据自己的需求进行定制和扩展，使Matlab更适应各种应用场景。

二、Matlab仿真建模的基本步骤Matlab中的仿真建模可以分为以下步骤：1. 确定仿真建模目标：首先，需要明确仿真的目标是什么，例如系统性能评估、控制策略设计等。

这有助于确定仿真的范围和需要建立的模型。

2. 收集输入数据：仿真建模需要用到输入数据，在确定仿真目标后，需收集和准备相应的输入数据。

输入数据可以是实验数据、统计数据或者通过其他模型得到的数据。

3. 建立模型：根据仿真的目标，使用Matlab编写代码，建立合适的数学模型。

在建立模型过程中，可借助Matlab提供的内置函数和工具箱，以及自己编写的辅助函数。

4. 设定参数和初始条件：模型的运行需要设定相应的参数和初始条件。

第一篇MATLAB入门第1章MATLAB简介MATLAB（Matrix Laboratory）是由MathWorks公司于1984年推出的一套科学计算软件，分为总包和若干个工具箱。

它具有强大的矩阵计算和数据可视化能力。

1.1 MATLAB的主要特点该软件的主要特点：⑴简单易学：MATLAB是一门编程语言，其语法规则与一般的结构化高级编程语言大同小异，而且使用更方便，具有一般语言基础的用户很快就可以掌握。

⑵代码短小高效：由于MATLAB已经将数学问题的具体算法编成了现成的函数，用户只要熟悉算法的特点、使用场合、函数的调用格式和参数意义等，通过调用函数很快就可以解决问题，而不必花大量的时间纠缠于具体算法的实现。

⑶计算功能非常强大：该软件具有强大的矩阵计算功能，利用一般的符号和函数就可以对矩阵进行加、减、乘、除运算以及转置和求逆等运算，而且可以处理稀疏矩阵等特殊的矩阵，非常适合于有限元等大型数值算法的编程。

此外，该软件现有的数十个工具箱，可以解决应用中的很多数学问题。

⑷强大的图形绘制和处理功能：该软件可以绘制常见的二维三维图形，还可以对三维图形进行颜色、光照、材质、纹理和透明性设置并进行交互处理。

⑸可扩展性能：可扩展性能是该软件的一大优点，用户可以自己编写M文件，组成自己的工具箱，方便地解决本领域内常见的计算问题。

此外，利用MATLAB编译器可以生成独立的可执行程序，从而可以隐藏算法并避免依赖MATLAB。

1.2 MATLAB桌面简介启动MATLAB时，MA TLAB的桌面如图1－1。

可以根据需要改变桌面外观，包括移动、缩放和关闭工具窗口等。

MATLAB桌面包括表1－1中的几种工具窗口，在默认情况下，它们中间有一些没有显示。

1.2.1 启动按钮(“Start”)打开MATLAB主界面以后，单击“Start”按钮，显示一个菜单，利用“Start”菜单及其子菜单中的选项，可以直接打开MA TLAB的有关工具。

第三章云模型简介在人类认知以及进行决策过程中，语言文字是一种强有力的思维工具，它是人类智能和其他生物智能的根本区别。

人脑进行思维不是纯粹地应用数学知识，而是靠自然语言特别是客观事物在人脑中的反映而形成的概念。

以概念为基础的语言、理论、模型是人类描述和理解世界的方法。

自然语言中，常常通过语言值，也就是词来表示概念。

而语言值、词或概念与数学和物理的符号的最大区别就是其中包含太多的不确定性。

在人工智能领域，不确定性的研究方法有很多，主要有概率理论，模糊理论，证据理论和粗糙集理论；对于确定性系统的不确定性的研究还有混沌和分形的方法。

这些方法从不同的视角研究了不确定性，优点是：有切入点明确、边界条件约束清楚、能够对问题进行深入研究等，但是在研究中常常将不确定性分成模糊性和随机性分开进行研究，然而两者之间有很强的关联性，往往不能完全的分开。

随机性是指有明确定义但是不一定出现的事件中所包含的不确定性。

例如在投掷硬币试验中，硬币落地时要么有国徽的一面向上，要么标有分值的一面向上，结果是明确的可以预知的，但是每次试验结果是随机的。

概率论和数理统计是研究和揭示这种随机现象的一门学科，至今已有几百年的研究历史．模糊性是另一种不确定性，是已经出现的但是很难精确定义的事件中所包含的不确定性。

在日常工作和生活中存在着许多模糊概念，如“胖子”“年轻人”“收入较高”等。

为处理这些模糊概念，引入了模糊集的概念[41]，使用隶属度来刻画模糊事物彼此间的程度。

隶属度函数常用的确定方法有模糊统计法、例证法专家经验法等，这些方法确定隶属度函数的过程是确定的,本质上说是客观的,但每个人对于同一个模糊概念的认识理解存在差异,因此有很强的主观性，而且一旦隶属度函数确定之后，得到的概念、定理等包含着严密的数学思维，其不具有任何模糊性。

针对上述问题李德毅院士在传统的概率统计理论和模糊理论的基础上提出了定性定量不确定性转换模型——云模型，实现定性概念和定量值之间的不确定性转换。

如何使用MATLAB进行数学建模与分析第一章 MATLAB简介与安装MATLAB是一款强大的数值计算软件，广泛应用于科学计算、工程建模、数据处理和可视化等领域。

本章将介绍MATLAB的基本特点、主要功能以及安装方法。

首先，MATLAB具有灵活的编程语言，可以进行复杂的数学运算和算法实现。

其次，MATLAB集成了丰富的数学函数库，包括线性代数、优化、常微分方程等方面的函数，方便用户进行数学建模和分析。

最后，MATLAB提供了直观友好的图形界面，使得数据处理和结果展示更加便捷。

为了使用MATLAB进行数学建模与分析，首先需要安装MATLAB软件。

用户可以从MathWorks官网上下载最新版本的MATLAB安装程序，并按照提示进行安装。

安装完成后，用户需要根据自己的需要选择合适的许可证类型，并激活MATLAB软件。

激活成功后，用户将可以使用MATLAB的全部功能。

第二章 MATLAB基本操作与语法在开始进行数学建模与分析之前，用户需要了解MATLAB的基本操作和语法。

本章将介绍MATLAB的变量定义与赋值、矩阵运算、函数调用等基本操作。

首先，MATLAB使用变量来存储数据，并可以根据需要对变量进行重新赋值。

变量名可以包含字母、数字和下划线，但不允许以数字开头。

其次，MATLAB支持矩阵运算，可以方便地进行矩阵的加减乘除、转置和求逆等操作。

用户只需要输入相应的矩阵运算符和矩阵变量即可。

然后，MATLAB提供了丰富的数学函数，用户可以直接调用这些函数进行数学运算。

最后，用户可以根据需要编写自定义函数，实现更复杂的算法和数学模型。

第三章数学建模与优化数学建模是利用数学方法和技巧，对实际问题进行描述、分析和求解的过程。

本章将介绍如何使用MATLAB进行数学建模与优化。

首先，数学建模的第一步是问题描述和模型构建。

用户需要明确问题的目标、约束条件和决策变量，并将其转化为数学模型。

其次，用户可以使用MATLAB提供的优化函数，对数学模型进行求解。

1.绘制云图Ex=18En=2He=0.2hold onfor i=1:1000Enn=randn(1)*He+En;x(i)=randn(1)*Enn+Ex;y(i)=exp(-(x(i)-Ex)^2/(2*Enn^2)); plot(x(i),y(i),'*')endEx=48.7En=9.1He=0.39hold onfor i=1:1000Enn=randn(1)*He+En;x(i)=randn(1)*Enn+Ex;y(i)=exp(-(x(i)-Ex)^2/(2*Enn^2)); plot(x(i),y(i),'*')end2.求期望、熵及超熵X1=[51.93 52.51 54.70 43.14 43.85 44.48 44.61 52.08];Y1=[0.91169241573 0.921875 0.96032303371 0.75737359551 0.76983848315 0.7808988764 0.78318117978 0.9143258427];m=8;Ex=mean(X1)En1=zeros(1,m);for i=1:mEn1(1,i)=abs(X1(1,i)-Ex)/sqrt(-2*log(Y1(1,i)));endEn=mean(En1);He=0;for i=1:mHe=He+(En1(1,i)-En)^2;endEn=mean(En1)He=sqrt(He/(m-1))3.平顶山so2环境:X1=[0.013 0.04 0.054 0.065 0.07 0.067 0.058 0.055 0.045];Y1=[0.175675676 0.540540541 0.72972973 0.8783783780.945945946 0.905405405 0.783783784 0.743243243 0.608108108]; m=9;Ex=mean(X1)En1=zeros(1,m);for i=1:mEn1(1,i)=abs(X1(1,i)-Ex)/sqrt(-2*log(Y1(1,i)));endEn=mean(En1);He=0;for i=1:mHe=He+(En1(1,i)-En)^2;endEn=mean(En1)He=sqrt(He/(m-1))1.绘制正向云图Ex=18En=2He=0.2hold onfor i=1:1000Enn=randn(1)*He+En;x(i)=randn(1)*Enn+Ex;y(i)=exp(-(x(i)-Ex)^2/(2*Enn^2));plot(x(i),y(i),'*')endEx=48.7En=9.1He=0.39hold onfor i=1:1000Enn=randn(1)*He+En;x(i)=randn(1)*Enn+Ex;y(i)=exp(-(x(i)-Ex)^2/(2*Enn^2));plot(x(i),y(i),'*')end2.逆向云发生器中需要剔除隶属度大于0. 9999 的云滴，剩下个云滴。

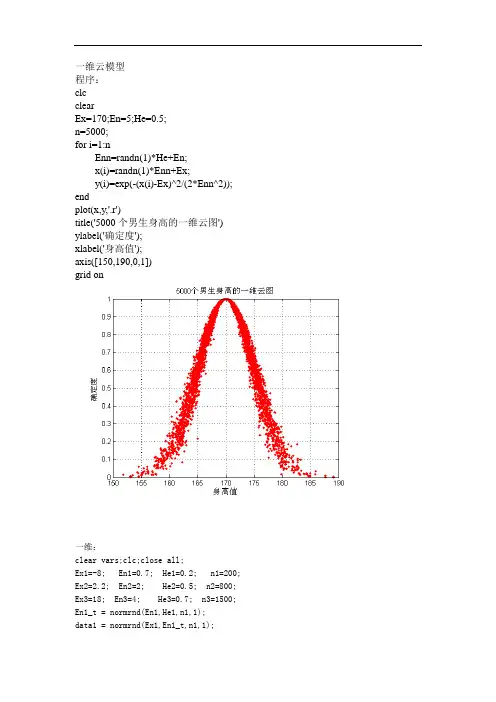
一维云模型程序：clcclearEx=170;En=5;He=0.5;n=5000;for i=1:nEnn=randn(1)*He+En;x(i)=randn(1)*Enn+Ex;y(i)=exp(-(x(i)-Ex)^2/(2*Enn^2)); endplot(x,y,'.r')title('5000个男生身高的一维云图') ylabel('确定度');xlabel('身高值');axis([150,190,0,1])grid on一维：clear vars;clc;close all;Ex1=-8; En1=0.7; He1=0.2; n1=200; Ex2=2.2; En2=2; He2=0.5; n2=800; Ex3=18; En3=4; He3=0.7; n3=1500; En1_t = normrnd(En1,He1,n1,1);data1 = normrnd(Ex1,En1_t,n1,1);mu1 = exp(-0.5*((data1-Ex1)./En1_t).^2);En2_t = normrnd(En2,He2,n2,1);data2 = normrnd(Ex2,En2_t,n2,1);mu2 = exp(-0.5*((data2-Ex2)./En2_t).^2);En3_t = normrnd(En3,He3,n3,1);data3 = normrnd(Ex3,En3_t,n3,1);mu3 = exp(-0.5*((data3-Ex3)./En3_t).^2);figure(1);plot(data1,mu1,'.b',data2,mu2,'*r',data3,mu3,'+k'); axis equal;二维云模型程序：clcclearEx1=170;En1=5;He1=0.5;Ex2=65;En2=3;He2=0.2;n=5000;for i=1:nEnn1=randn(1)*He1+En1;x1(i)=randn(1)*Enn1+Ex1;Enn2=randn(1)*He2+En2;x2(i)=randn(1)*Enn2+Ex2;y(i)=exp(-(x1(i)-Ex1)^2/(2*Enn1^2)-(x2(i)-Ex2)^2/(2*Enn2^2)); endplot3(x1,x2,y,'.r')title('5000个男生身高体重的二维云图')axis([148,190,50,80,0,1])grid on结果：多个一维clear vars;clc;close all;Ex1=0; En1=0.103; He1=0.013; n1=5000;Ex2=0.309; En2=0.064; He2=0.008; n2=5000;Ex3=0.5; En3=0.039; He3=0.005; n3=5000;Ex4=0.691; En4=0.064; He4=0.008; n4=5000;Ex5=1; En5=0.103; He5=0.013; n5=5000;En1_t = normrnd(En1,He1,n1,1);data1 = normrnd(Ex1,En1_t,n1,1);mu1 = exp(-0.5*((data1-Ex1)./En1_t).^2);En2_t = normrnd(En2,He2,n2,1);data2 = normrnd(Ex2,En2_t,n2,1);mu2 = exp(-0.5*((data2-Ex2)./En2_t).^2);En3_t = normrnd(En3,He3,n3,1);data3 = normrnd(Ex3,En3_t,n3,1);mu3 = exp(-0.5*((data3-Ex3)./En3_t).^2);En4_t = normrnd(En4,He4,n4,1);data4 = normrnd(Ex4,En4_t,n4,1);mu4 = exp(-0.5*((data4-Ex4)./En4_t).^2);En5_t = normrnd(En5,He5,n5,1);data5 = normrnd(Ex5,En5_t,n5,1);mu5 = exp(-0.5*((data5-Ex5)./En5_t).^2);figure(1);plot(data1,mu1,'.r',data2,mu2,'.r',data3,mu3,'.r',data4,mu4,'.r',data5,mu5,'.r' );title('评价集')ylabel('隶属度');axis([-0.4,1.4,0,1])grid on一维Ex=1100;En=84.926;He=0.1;n=1000;X=zeros(1,n);Y=zeros(1,n);X(1:n)=normrnd(En,He,1,n);for i=1:nEn1=X(1,i);X(1,i)=normrnd(Ex,En1,1);Y(1,i)=exp((-(X(1,i)-Ex)^2)/(2*En1^2));plot(X,Y,'.','MarkerEdgeColor','k','markersize',4); title('强等级','fontsize',16);grid on;end逆发生器代码X1=X ;Y1=Y;i=1;while i<=(n-flag)If Y1(1,i)>0.9999Y1(:,i)=[ ] ;X1(:,i)=[ ] ;flag=flag+1;End;Ex=mean(X1) ;En1=zeros(1,m) ;for i=1:m ;En1(1,i)=abs(X1(1,i)-Ex)/sqrt(-2*log(Y1(1,i))) ; End ;En=mean(En1) ;He=0 ;for i=1:m ;He=He+(En1(1,i)-En)^2 ;He=sqrt(He/(m-1)) ;End ;X1 =X;Y1=Y;i=1;while i<=(n-flag)if Y1(1,i)>0.9999Y1(:,i)=[];X1(:,i)=[];flag=flag+1;elsei=i+1;m=m +1;endendEx=mean(X1)En1=zeros(1,m);for i= l:mEn1(1,i)=abs(X1(1,i)-Ex)/sqrt(-2 *log(Y1(1,i))); endEn=mean(En1);He=0;for i=l:mHe=He+(En1(1,i)-En)^2;endHe=sqrt(He/(m-1))clear vars;clc;close all;Ex1=0.457; En1=0.150; He1=0.050; n1=4000; Ex2=0.454; En2=0.156; He2=0.056; n2=4000;Ex3=0.435; En3=0.229; He3=0.067; n3=4000;Ex4=0.415; En4=0.177; He4=0.071; n4=4000;Ex5=0.414; En5=0.298; He5=0.099; n5=4000; Ex6=0.410; En6=0.242; He6=0.061; n6=4000;Ex7=0.410; En7=0.188; He7=0.061; n7=4000;Ex8=0.500; En8=0.039; He8=0.005; n8=5000;En1_t = normrnd(En1,He1,n1,1);data1 = normrnd(Ex1,En1_t,n1,1);mu1 = exp(-0.5*((data1-Ex1)./En1_t).^2);En2_t = normrnd(En2,He2,n2,1);data2 = normrnd(Ex2,En2_t,n2,1);mu2 = exp(-0.5*((data2-Ex2)./En2_t).^2);En3_t = normrnd(En3,He3,n3,1);data3 = normrnd(Ex3,En3_t,n3,1);mu3 = exp(-0.5*((data3-Ex3)./En3_t).^2);En4_t = normrnd(En4,He4,n4,1);data4 = normrnd(Ex4,En4_t,n4,1);mu4 = exp(-0.5*((data4-Ex4)./En4_t).^2);En5_t = normrnd(En5,He5,n5,1);data5 = normrnd(Ex5,En5_t,n5,1);mu5 = exp(-0.5*((data5-Ex5)./En5_t).^2);En6_t = normrnd(En6,He6,n6,1);data6 = normrnd(Ex6,En6_t,n6,1);mu6 = exp(-0.5*((data6-Ex6)./En6_t).^2);En7_t = normrnd(En7,He7,n7,1);data7 = normrnd(Ex7,En7_t,n7,1);mu7 = exp(-0.5*((data7-Ex7)./En7_t).^2);En8_t = normrnd(En8,He8,n8,1);data8 = normrnd(Ex8,En8_t,n8,1);mu8 = exp(-0.5*((data8-Ex8)./En8_t).^2);figure(1);plot(data1,mu1,'.r',data2,mu2,'.r',data3,mu3,'.r',data4,mu4,'.r',data5,mu5,'.r' ,data6,mu6,'.r',data7,mu7,'.r',data8,mu8,'.r');title('评价集')ylabel('隶属度');axis([-0.4,1.4,0,1])grid onclear vars;clc;close all;Ex1=0.716; En1=0.123; He1=0.045; n1=4000;Ex2=0.545; En2=0.140; He2=0.052; n2=4000;Ex3=0.534; En3=0.233; He3=0.085; n3=4000;Ex4=0.461; En4=0.202; He4=0.063; n4=4000;Ex5=0.691; En5=0.064; He5=0.008; n5=6000;En1_t = normrnd(En1,He1,n1,1);data1 = normrnd(Ex1,En1_t,n1,1);mu1 = exp(-0.5*((data1-Ex1)./En1_t).^2);En2_t = normrnd(En2,He2,n2,1);data2 = normrnd(Ex2,En2_t,n2,1);mu2 = exp(-0.5*((data2-Ex2)./En2_t).^2);En3_t = normrnd(En3,He3,n3,1);data3 = normrnd(Ex3,En3_t,n3,1);mu3 = exp(-0.5*((data3-Ex3)./En3_t).^2);En4_t = normrnd(En4,He4,n4,1);data4 = normrnd(Ex4,En4_t,n4,1);mu4 = exp(-0.5*((data4-Ex4)./En4_t).^2);En5_t = normrnd(En5,He5,n5,1);data5 = normrnd(Ex5,En5_t,n5,1);mu5 = exp(-0.5*((data5-Ex5)./En5_t).^2);figure(1);plot(data1,mu1,'.r',data2,mu2,'.r',data3,mu3,'.r',data4,mu4,'.r',data5,mu5,'.r' );title('评价集')ylabel('隶属度');axis([-0.4,1.4,0,1]) grid on。

利用Matlab绘制云模型许大亮【摘要】The cloud model is an uncertainty model for transformation between qualitative concept and quantitative descrip-tion, then it can express qualitative concept and process quantitative calculation. The development of cloud model is from one-dimension to two-dimension and even multidimensional model at present.As a result, it is used to represent more compli-cated natural language concept. This paper mainly introduces the one-dimension and two-dimension normal cloud generator implementation algorithm.In addition, the Matlab implements cloud generator algorithm and draws the graphs of two different dimension cloud models.%云模型是定性概念与定量描述的不确定性转换模型，可以用来表示定性概念并进行定量计算。

目前云模型由一维发展到二维甚至多维，这样就可以利用它表示更加复杂的自然语言概念。

介绍了一维和二维云模型的正向云发生器，并用Matlab语言实现了云模型算法，绘制了两种不同维数云模型的图形。

【期刊名称】《科技创新与生产力》【年(卷),期】2016(000)001【总页数】3页(P108-110)【关键词】云模型;不确定性;正向云发生器;Matlab【作者】许大亮【作者单位】安徽理工大学测绘学院，安徽淮南 232001【正文语种】中文【中图分类】G202E-mail：*****************。

目录：1.MATLAB 简介2.MATLAB 的优势3.MATLAB 的应用领域4.MATLAB 基础语法5.MATLAB 编程技巧6.MATLAB 的工具箱7.我的使用体验8.结论1. MATLAB 简介MATLAB 是一种高级的数学软件和编程语言，广泛应用于科学计算、数据分析、工程模拟和算法开发等领域。

它由 MathWorks 公司开发，具有强大的数值计算和图形处理能力，并且易于上手和学习。

2. MATLAB 的优势MATLAB 具有以下几个优势：•简单易学：MATLAB 的语法设计简洁明了，与数学领域的符号表达相近，使得使用者可以快速上手。

•丰富的工具库：MATLAB 提供了众多的工具箱，涵盖了信号处理、图像处理、控制系统、优化算法等多个领域，方便用户进行各种科学计算和工程应用。

•强大的数值计算能力：MATLAB 采用矩阵运算的思想，能够高效地处理向量和矩阵运算，大大减少了编写循环代码的复杂性。

•优秀的图形展示功能：MATLAB 提供了丰富的绘图函数和工具，用户可以方便地生成高质量的二维或三维图形，用于数据可视化和结果展示。

•广泛的社区支持：MATLAB 拥有庞大的用户社区，用户可以在网上查找各种问题的解答和代码示例，便于学习和解决实际问题。

3. MATLAB 的应用领域MATLAB 在各个领域都有广泛的应用，包括但不限于：•工程学科：MATLAB 可以帮助工程师进行信号处理、控制系统设计、系统仿真、图像处理等工作。

•科学研究：MATLAB 可以用于数据分析、统计建模、数学模拟、算法开发等科学研究工作。

•金融领域：MATLAB 提供了专门的金融工具箱，可以用于投资组合分析、金融风险评估、衍生品定价等金融相关的计算任务。

•生物医学：MATLAB 在生物信号处理、遗传算法、图像处理等方面有着广泛的应用。

•教育领域：MATLAB 作为一种易学易用的编程语言，被广泛应用于高校和中学的数学和工程教育中。

Only in boiling water, tea can develop the rich aroma of life.简单易用轻享办公（页眉可删）Matlab学习心得与体会Matlab学习心得与体会篇一：MATLAB学习心得一．对MATLAB的认识正如课本《MATLAB教程及实训》中的前言所说，MATLAB是MathWords公司于1984年开发的，目前已经发展成国际上最流行、应用最广泛的科学与工程计算软件之一。

MATLAB集合矩阵云运算、数值分析、图形显示和仿真等于一体，被广泛应用于自动控制、数学运算、计算机技术、图像信号处理、汽车工业、语音处理等行业。

MATLAB它将计算、可视化和编程等功能同时集于一个易于开发的环境。

MATLAB主要应用于数学计算、系统建模与仿真、数学分析与可视化、科学与工程制图和用户界面设计等。

目前，MATLAB已经成为应用代数、自动控制理论、数字信号处理、动态系统仿真和金融等专业的基本数学工具，各国高校纷纷将MATLAB正式列入本科生和研究生课程的教书计划中，成为学生必须掌握的软件之一。

MATLAB是matrix laboratory的缩写，它的产生是与数学计算有密切的关系。

从1980年发展到现在已经是一个交互式开发系统，其基本数据要素是矩阵。

MATLAB系统是由MATLAB开发环境和MATLAB语言，MATLAB数学函数库、MATLAB图形处理系统和MATLAB应用程序接口（APL）5部分组成。

MATLAB的有以下特点1运算功能强大 2编程效率高3强大而智能化的作图功能 4可扩展性强 5Simulink 动态仿真功能二．我对MATLAB的掌握程度在短课时选择了本书1、2、3、4、5、7章的内容学习1. MATLAB R20__a软件的概述(略)。

2. MATLAB常见字符及基本运算在本人的自主学习以及老师的授课下我已经初略的掌握了MATLAB R20__a的基本使用方法：MATLAB R20__a的开发环境、MATLAB R20__a的其他管理、MATLAB的文件处理工具、MATLAB R20__a的帮助系统（1）数据类型数组：字符型、数值型、元胞型、结构体型、Java型和函数句柄，其中数值型有包括单精度型和双精度型。