圆柱的侧面积、表面积、体积计算

所有体积表面积侧面积公式
一、正方体。

1. 体积公式：V = a^3（a为正方体的棱长）
2. 表面积公式：S = 6a^2
3. 侧面积公式：正方体的侧面有4个正方形，每个正方形边长为a，所以侧面积S_侧=4a^2
二、长方体。

1. 体积公式：V=abh（a、b、h分别为长方体的长、宽、高）
2. 表面积公式：S = 2(ab+ah+bh)
3. 侧面积公式：长方体侧面积S_侧=2h(a + b)
三、圆柱。

1. 体积公式：V=π r^2h（r为底面半径，h为圆柱的高）
2. 表面积公式：S = 2π r^2+2π rh
3. 侧面积公式：S_侧=2π rh
四、圆锥。

1. 体积公式：V=(1)/(3)π r^2h（r为底面半径，h为圆锥的高）
2. 表面积公式：S=π r^2+π rl（l为圆锥的母线长，l = √(r^2)+h^{2}）
3. 侧面积公式：S_侧=π rl
五、球。

1. 体积公式：V=(4)/(3)π R^3（R为球的半径）
2. 表面积公式：S = 4π R^2，球没有侧面积概念（因为球是一个完全对称的几何体）。

圆柱圆锥的表面积公式和体积公式是什么？
圆锥体积：V=1/3Sh（S是底面积，h是高）。

圆锥表面积的计算公式是：圆锥的表面积＝底面积＋侧面积（侧面积将圆锥的侧面积不成曲线地展开，是一个扇形。

），用字母表示就是S=πr²+πrl（其中l=母线，是圆锥的顶点到圆锥的底面圆周之间的距离）。

圆柱体体积公式：圆柱体积＝π＊r²*h=S底面积＊高（h）；先求底面积，然后乘高。

圆柱体积公式是用于计算圆柱体体积的公式。

圆柱体表面积公式：S=2πr(r+h)。

π是圆周率，r是圆柱底面的半径，h是圆柱体的高。

相关公式
正方形的周长＝边长×4
长方形的面积＝长×宽
长方形的周长＝（长＋宽）×2
正方形的面积＝边长×边长
三角形的面积＝底×高÷2
平行四边形的面积＝底×高
梯形的面积＝（上底＋下底）×高÷2
直径＝半径×2半径＝直径÷2
圆的周长＝圆周率×直径＝圆周率×半径×2圆的面积＝圆周率×半径×半径。

圆柱的表面积和体积计算圆柱是一种常见的几何体，它由一个圆和一个垂直于圆的轴线组成，而圆柱的表面积和体积是我们在数学中经常需要计算的内容。

下面，我们将详细介绍圆柱表面积和体积的计算方法。

一、圆柱的表面积计算圆柱的表面积包括圆的面积和侧面的面积。

首先，我们来计算圆的面积。

圆的面积公式为：S=πr^2，其中π取值约为3.14159，r为圆的半径。

接下来，我们计算圆柱的侧面积。

对于一个圆柱而言，它的侧面可以展开成一个矩形。

而矩形的面积公式为：S=2πrh，其中π取值约为3.14159，r为圆的半径，h为圆柱的高度。

所以，圆柱的表面积等于圆的面积加上侧面的面积，即S=πr^2+2πrh。

二、圆柱的体积计算圆柱的体积是指圆柱所占据的空间大小。

它的计算公式为：V=πr^2h，其中π取值约为3.14159，r为圆的半径，h为圆柱的高度。

三、实例分析为了更好地理解圆柱表面积和体积的计算方法，我们来做一个实例分析。

假设有一个圆柱，其半径为3cm，高度为5cm。

首先，计算圆柱的表面积。

根据前面的公式，我们可以得到表面积的计算公式为S=πr^2+2πrh。

将半径r和高度h代入计算公式中，得到S=3.14159*3^2+2*3.14159*3*5=165.39cm^2。

接下来，计算圆柱的体积。

根据圆柱体积的计算公式V=πr^2h，将半径r和高度h代入计算公式中，得到V=3.14159*3^2*5=141.37cm^3。

四、小结通过以上的介绍和实例分析，我们了解到圆柱的表面积和体积的计算方法。

需要注意的是，在实际计算过程中，我们应该根据具体的数值进行计算，并保留适当的小数位数。

另外，在计算过程中，也可以利用计算器等工具来提高计算的准确性和效率。

总之，圆柱的表面积和体积计算是数学中的基础内容，掌握计算方法可以帮助我们更好地理解并应用几何概念。

希望通过本文的介绍，您对圆柱的表面积和体积计算有所了解与掌握。

圆柱体侧面积计算的公式
公式：侧面积=底面周长×高；侧面积=半径×2×3.14×高；侧面积=直径×3.14×高。

圆柱是由两个大小相等、相互平行的圆形（底面）以及连接两个底面的一个曲面（侧面）围成的几何体。

圆柱体性质
1.圆柱的两个圆面叫底面，周围的面叫侧面，一个圆柱体是由两个底面和一个侧面组成的。

2.圆柱体的两个底面是完全相同的两个圆面。

两个底面之间的距离是圆柱体的高。

3.圆柱的体积=底面积x高，即V=S底面积×h=(π×r×r)h
4.等底等高的圆柱的体积是圆锥的3倍。

5.圆柱体可以用一个平行四边形围成。

6.圆柱的表面积=侧面积+底面积x2。

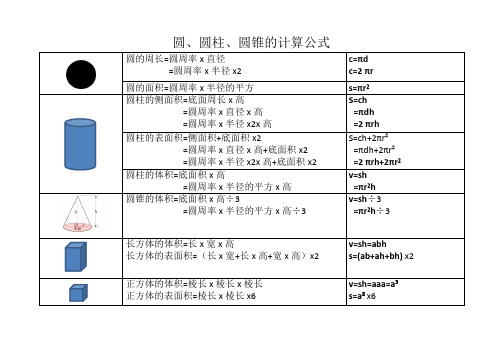
圆、圆柱、圆锥的计算公式
圆的周长=圆周率x直径
=圆周率x半径x2 c=πd c=2 πr
圆的面积=圆周率x半径的平方s=πr²
圆柱的侧面积=底面周长x高
=圆周率x直径x高
=圆周率x半径x2x高S=ch =πdh =2 πrh
圆柱的表面积=侧面积+底面积x2
=圆周率x直径x高+底面积x2
=圆周率x半径x2x高+底面积x2 S=ch+2πr²
=πdh+2πr²=2 πrh+2πr²
圆柱的体积=底面积x高
=圆周率x半径的平方x高v=sh =πr²h
圆锥的体积=底面积x高÷3
=圆周率x半径的平方x高÷3 v=sh÷3 =πr²h÷3
长方体的体积=长x宽x高
长方体的表面积=（长x宽+长x高+宽x高）x2 v=sh=abh
s=(ab+ah+bh) x2
正方体的体积=棱长x棱长x棱长正方体的表面积=棱长x棱长x6 v=sh=aaa=a³s=a²x6。

圆柱的表面积体积公式圆柱是一种常见的几何体，它由一个圆形底面和一个平行于底面的圆柱体侧面组成。

圆柱的表面积和体积是我们在学习数学和物理时经常会涉及的概念。

在本文中，我们将探讨圆柱的表面积和体积公式，并介绍一些应用。

首先，让我们来看看圆柱的表面积公式。

圆柱的表面积是指其底面和侧面的总面积。

假设圆柱的底面半径为r，高为h，则其表面积公式为：S = 2πr + 2πrh其中，2πr是底面的面积，2πrh是侧面的面积。

这个公式的推导可以通过将圆柱展开成一个矩形来得到。

具体来说，我们可以将圆柱的侧面展开成一个矩形，其长为2πr，宽为h。

然后，将底面的面积2πr加上侧面矩形的面积2πrh，即可得到圆柱的表面积。

接下来，我们来看看圆柱的体积公式。

圆柱的体积是指其底面和侧面组成的空间大小。

假设圆柱的底面半径为r，高为h，则其体积公式为：V = πrh这个公式的推导可以通过将圆柱的侧面切割成若干个薄片来得到。

具体来说，我们可以将圆柱的侧面切割成n个薄片，每个薄片的宽度为Δh。

然后，将每个薄片的面积πrΔh加起来，即可得到圆柱的体积。

圆柱的表面积和体积公式在数学和物理中有着广泛的应用。

例如，在工程中，我们经常需要计算圆柱形的管道、容器和筒体的表面积和体积。

在建筑设计中，圆柱形的柱子和圆筒形的塔楼也需要用到这些公式。

此外，在物理中，圆柱形的轮子和滚筒也需要用到这些公式。

除了圆柱，其他几何体的表面积和体积公式也是非常重要的。

例如，长方体的表面积公式为S = 2lw + 2lh + 2wh，体积公式为V = lwh；球体的表面积公式为S = 4πr，体积公式为V = (4/3)πr。

掌握这些公式可以帮助我们更好地理解和应用数学和物理知识。

总之，圆柱的表面积和体积公式是数学和物理中的基础概念。

通过掌握这些公式，我们可以更好地理解和应用几何体的知识。

希望本文能够对读者有所帮助。

圆柱体与圆锥体的计算方法圆柱体和圆锥体是几何学中常见的立体图形。

在进行计算时，我们需要掌握一些基本的计算方法，以便求解其体积、表面积和侧面积等相关参数。

下面将详细介绍圆柱体和圆锥体的计算方法。

一、圆柱体的计算方法圆柱体是由一个底面为圆形的圆筒和两个平行于底面的圆盖组成的立体。

求解圆柱体的体积、表面积和侧面积等参数时，我们需要以下一些计算方法：1. 圆柱体的体积计算方法圆柱体的体积是指圆柱体内部可以容纳的空间大小。

计算圆柱体的体积时，我们需要知道圆柱体的底面半径r和高h。

圆柱体的体积公式如下：V = π * r² * h其中，V表示圆柱体的体积，π为圆周率，r为底面圆的半径，h为圆柱体的高度。

2. 圆柱体的表面积计算方法圆柱体的表面积是指圆柱体所有表面的总面积。

计算圆柱体的表面积时，我们需要知道圆柱体的底面半径r和高h。

圆柱体的表面积公式如下：S = 2 * π * r² + 2 * π * r * h其中，S表示圆柱体的表面积，π为圆周率，r为底面圆的半径，h 为圆柱体的高度。

3. 圆柱体的侧面积计算方法圆柱体的侧面积是指圆柱体侧边的面积。

计算圆柱体的侧面积时，我们需要知道圆柱体的底面半径r和高h。

圆柱体的侧面积公式如下：A = 2 * π * r * h其中，A表示圆柱体的侧面积，π为圆周率，r为底面圆的半径，h 为圆柱体的高度。

二、圆锥体的计算方法圆锥体是由一个底面为圆形的圆锥和一个连接底面中心与顶点的侧面组成的立体。

求解圆锥体的体积、表面积和侧面积等参数时，我们需要以下一些计算方法：1. 圆锥体的体积计算方法圆锥体的体积是指圆锥体内部可以容纳的空间大小。

计算圆锥体的体积时，我们需要知道底面圆的半径r和圆锥体的高h。

圆锥体的体积公式如下：V = (1/3) * π * r² * h其中，V表示圆锥体的体积，π为圆周率，r为底面圆的半径，h为圆锥体的高度。

2. 圆锥体的表面积计算方法圆锥体的表面积是指圆锥体所有表面的总面积。

圆柱和圆锥的表面积公式和体积公式圆柱和圆锥的表面积公式和体积公式圆柱和圆锥是几何形体中比较常见的一种，它们都具有旋转对称性，因此具有一些比较特殊的性质。

本文将介绍圆柱和圆锥的表面积公式和体积公式，其中包括基本的公式推导和应用实例。

一、圆柱的表面积公式和体积公式圆柱是由一对平行于底面的圆面和一个连接两个圆面的侧面组成的。

下面分别介绍圆柱的表面积公式和体积公式。

1. 表面积公式圆柱的表面积可以看做是由两个底面和一个侧面组成。

底面的面积为圆面积，侧面的面积为矩形面积，因此圆柱的表面积公式可以表示为：S = 2πr² + 2πrh其中，S为圆柱的表面积，r为圆柱的底面半径，h为圆柱的高。

在实际应用中，我们常常需要计算圆柱的侧面积，即矩形的面积。

可以将圆柱展开成一个矩形，用矩形的面积公式进行计算。

2. 体积公式圆柱的体积可以看做是由底面面积和高度组成的。

圆柱的高度就是圆柱的侧面的长度，因此圆柱的体积公式可以表示为：V = πr²h其中，V为圆柱的体积。

二、圆锥的表面积公式和体积公式圆锥是由一个圆锥面和一个连接圆锥面的点并且垂直于底面的直线组成的。

下面分别介绍圆锥的表面积公式和体积公式。

1. 表面积公式圆锥的表面积可以看做是由底面和锥面组成。

锥面的面积可以通过毕达哥拉斯定理计算得到，因此圆锥的表面积公式可以表示为：S = πr² + πrl其中，S为圆锥的表面积，r为圆锥的底面半径，l为圆锥的斜高。

在实际应用中，我们常常需要计算圆锥的侧面积，即锥面的面积。

可以将圆锥展开成一个扇形和一个三角形，用扇形的面积公式和三角形的面积公式进行计算。

2. 体积公式圆锥的体积可以看做是由底面面积、高度和一个三角锥面积组成的。

圆锥的高度就是连接底面和顶点的直线的长度，因此圆锥的体积公式可以表示为：V = 1/3 × πr²h其中，V为圆锥的体积。

三、应用实例下面通过一些具体的实例来应用圆柱和圆锥的表面积公式和体积公式。

圆柱体侧面积公式表面积公式圆柱体体积公式圆柱体是一种几何体，由两个平行且相等的圆底面联结而成。

圆柱体的侧面是由底面沿着垂直于底面的方向移动所得的表面，可以看作是一个长方形的形状，高度等于圆柱体的高。

1.圆柱体的侧面积公式：
圆柱体的侧面积可以通过将它展开成一个矩形，再计算矩形的面积来求得。

矩形的长为圆的周长，即2πr，宽为圆柱体的高度h。

因此，圆柱体的侧面积公式可以表示为：
侧面积=周长×高度=2πr×h
2.圆柱体的表面积公式：
圆柱体的表面积由两个底面和一个侧面构成。

圆柱体的底面积为圆的面积，即πr²。

假设圆柱体的高为h，则两个底面的面积共为2πr²。

另外，圆柱体的侧面积为2πrh。

所以，圆柱体的表面积公式可以表示为：表面积 = 2底面积 + 侧面积= 2πr² + 2πrh = 2πr(r + h)
3.圆柱体的体积公式：
圆柱体的体积可以通过将其底面面积乘以高度来计算。

圆柱体的底面面积为πr²，且高度为h，所以圆柱体的体积公式可以表示为：体积=底面积×高度=πr²×h
以上是圆柱体侧面积、表面积和体积的公式。

这些公式在几何学和实际生活中都有重要的应用。

在工程领域，圆柱体的体积公式可以用来计算容器的容积；在建筑领域，圆柱体的表面积公式可以用来计算柱子的表面
积；在物理学中，圆柱体的侧面积公式可以用来计算液体流动的表面积等等。

圆柱体积公式表面积公式在同一个平面内有一条定直线和一条动线，当这个平面绕着这条定直线旋转一周时，这条动线所成的面叫做旋转面，这条定直线叫做旋转面的轴，这条动线叫做旋转面的母线。

如果用垂直于轴的两个平面去截圆柱面，那么两个截面和圆柱面所围成的几何体叫做直圆柱，简称圆柱体。

圆柱体体积公式圆柱体积公式是用于计算圆柱体体积的公式。

圆柱体积=π*r2*h=S底面积*高（h）先求底面积，然后乘高。

圆柱体表面积公式π是圆周率，r是圆柱底面的半径，h是圆柱体的高S=2πrr+h相关公式正方形的周长=边长×4长方形的面积=长×宽长方形的周长=（长+宽）×2正方形的面积=边长×边长三角形的面积=底×高÷2平行四边形的面积=底×高梯形的面积=（上底+下底）×高÷2直径=半径×2 半径=直径÷2圆的周长=圆周率×直径=圆周率×半径×2圆的面积=圆周率×半径×半径长方体的表面积=（长×宽+长×高＋宽×高）×2长方体的体积=长×宽×高正方体的表面积=棱长×棱长×6正方体的体积=棱长×棱长×棱长圆柱的侧面积=底面圆的周长×高圆柱的表面积=上下底面面积+侧面积圆柱的体积=底面积×高圆锥的体积=底面积×高÷3长方体（正方体、圆柱体）的体积=底面积×高感谢您的阅读，祝您生活愉快。