六年级数学圆柱的侧面积和表面积的计算

六年级下册-打印版
圆柱侧面积的计算方法
知识回顾长方形的面积=长×宽，用字母表示为S=ab；正方形的面积=边长×边长，用字母表示为S=a2。

问题导入怎样计算圆柱的侧面积呢？
过程讲解
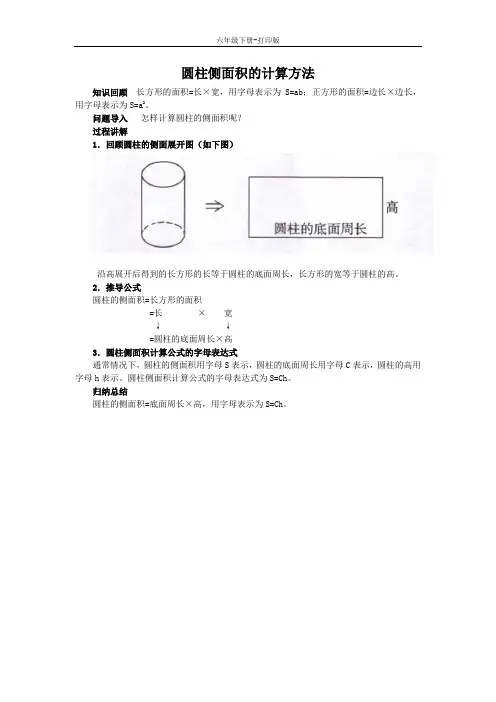
1．回顾圆柱的侧面展开图（如下图）
沿高展开后得到的长方形的长等于圆柱的底面周长，长方形的宽等于圆柱的高。

2．推导公式
圆柱的侧面积=长方形的面积
=长×宽
↓↓
=圆柱的底面周长×高
3．圆柱侧面积计算公式的字母表达式
通常情况下，圆柱的侧面积用字母S表示，圆柱的底面周长用字母C表示，圆柱的高用字母h表示。

圆柱侧面积计算公式的字母表达式为S=Ch。

归纳总结
圆柱的侧面积=底面周长×高，用字母表示为S=Ch。

圆柱的侧面积和表面积公式首先，让我们先介绍一下什么是圆柱。

圆柱是一个由两个平行相等的圆底面和它们之间的侧面组成的几何体。

其中，圆底面的直径称为圆柱的底面直径，它与底面上的圆心距离称为圆柱的高。

1.圆柱的侧面积公式：侧面积=底面周长×高侧面积=2πr×h其中，r是圆柱的底面半径，h是圆柱的高。

2.圆柱的表面积公式：圆柱的表面积等于两个底面加上侧面的总面积，即：表面积=2×底面积+侧面积表面积=2×πr²+2πr×h表面积=2πr×(r+h)其中，r是圆柱的底面半径，h是圆柱的高。

通过上述公式，我们可以计算出圆柱的侧面积和表面积。

下面我们将通过一些实际问题的应用案例来具体应用这些公式。

案例一：假设一个圆柱的底面半径为5cm，高为10cm，求该圆柱的侧面积和表面积。

根据圆柱的侧面积公式计算侧面积：侧面积=2πr×h侧面积=2π×5×10侧面积= 100π cm²根据圆柱的表面积公式计算表面积：表面积=2πr×(r+h)表面积=2π×5×(5+10)表面积=2π×5×15表面积= 150π cm²所以，该圆柱的侧面积为100π cm²，表面积为150π cm²。

案例二：一个铁管的内径为7cm，高度为30cm，如果该管的厚度为2cm，求这个铁管的侧面积和表面积。

首先，我们需要计算出铁管的外径。

由于铁管的厚度为2cm，所以外径等于内径加上2倍的厚度。

外径=内径+2×厚度外径=7+2×2外径 = 11cm根据圆柱的侧面积公式计算侧面积：侧面积=2πr×h侧面积=2π×11×30侧面积= 660π cm²根据圆柱的表面积公式计算表面积：表面积=2πr×(r+h)表面积=2π×11×(11+30)表面积=2π×11×41表面积= 902π cm²所以，这个铁管的侧面积为660π cm²，表面积为902π cm²。

圆柱体积的计算公式圆柱的体积和表面积怎么算
圆柱体的体积和面积计算公式是什幺？如何计算圆柱的体积与表面积？ 
 圆柱的体积和表面积如何计算圆柱体的体积计算公式：
 圆柱体的体积=底面积×高=（V=πr²h）；圆的面积=圆周率×半径×半径。

 圆柱的侧面积=底面圆的周长×高
 圆柱的表面积=上下底面面积+侧面积
 圆柱体的表面积计算公式：
 圆柱表面积：S表=2πr*r+2πrh
 常用数学图形计算公式长方形的周长=（长+宽）×2
 正方形的周长=边长×4
 长方形的面积=长×宽
 正方形的面积=边长×边长
 三角形的面积=底×高÷2
 平行四边形的面积=底×高
 梯形的面积=（上底+下底）×高÷2
 直径=半径×2 半径=直径÷2
 圆的周长=圆周率×直径=
 圆周率×半径×2
 圆的面积=圆周率×半径×半径
 长方体的表面积=
 （长×宽+长×高＋宽×高）×2
 长方体的体积=长×宽×高。

六年级数学圆柱的侧面积和表面积的计算
圆柱的侧面积和表面积的计算
永川市永红学校
授课教师：任润虎复习：准备活动：3.14×2=1、口算：
6.283.14×3=9.423.14×4=12.563.14×5=15.73.14×6=18.843.14×7=21.983.14×8=25. 123.14×9=28.263.14×10=31.43.14×20=62.83.14×0.5=1.573.14×0.1=0.314复习：准备活动：
2、计算：121144169196225256289324361400250010000 复习：准备活动：
周长：3.14×4=
3、计算：在圆中，
(1)、已知d=4 厘米，求C=？S=？
12.56(厘米)
面积：3.14×3.14×4=12.56(平方厘米)
周长：2×3.14×4=
(1)、已知r =4 分米，求C=？S=？
面积：3.14×3.14×16=50.24(平方分米)
25.12(分米)复习：准备活动：
4、圆柱体的各部分名称和特征
是什幺？
圆柱体侧面积计算公式的推导：
进入角色：
∴圆柱体的侧面积=底面周长×高
∵圆柱体的侧面展开是一个长方形，这个长方形的长等于圆柱底面的周。

圆柱的外表面积公式
圆柱，作为三维几何体的一种，具有独特的形态美和丰富的数学属性。

它的外表面积，指的是圆柱体外部所占据的面积，是数学和物理领域中经常需要计算的一个量。

圆柱的表面积是由其底面和顶面以及侧面所组成的。

底面是一个圆，其面积计算公式为πr²，其中r是圆的半径。

这个公式描述了圆的面积与半径之间的关系，是数学中一个基础而重要的公式。

顶面与底面完全相同，因此其面积也是πr²。

侧面则是一个曲面，其面积的计算稍微复杂一些。

侧面积是由圆柱的高h和底面的周长c所决定的。

周长c可以通过公式2πr计算，因此侧面积的计算公式为ch=2πrh。

这个公式揭示了圆柱侧面积与其高和底面半径之间的联系。

将底面积和侧面积相加，就可以得到圆柱的总表面积。

因此，圆柱的表面积公式为S=ch=πdh=2πrh。

这个公式简洁明了地表达了圆柱表面积与各参数之间的关系。

另外，还有一个扩展的表面积公式S=2πr(r+h)，这个公式在某些情况下更为实用。

它通过将底面半径和高的线性组合与π相乘，简化了计算过程。

这个公式突出了圆柱表面积与其各部分尺寸之间的紧密关系。

无论是基础公式还是扩展公式，它们都体现了数学在描述形状特性方面的强大和简洁。

通过这些公式，我们可以方便地计算出圆柱的表面积，从而进一步研究其几何属性和与其他形状的关系。

2021-2022学年六年级数学下册典型例题系列之第二单元圆柱的表面积问题基础部分（解析版）编者的话：《2021-2022学年六年级数学下册典型例题系列》是基于教材知识点和常年考点考题总结与编辑而成的，该系列主要包含典型例题和专项练习两大部分。

典型例题部分是按照单元顺序进行编辑，主要分为计算和应用两大部分，其优点在于考题典型，考点丰富，变式多样。

专项练习部分是从常考题和期末真题中选取对应练习，其优点在于选题经典，题型多样，题量适中。

本专题是第二单元圆柱的表面积问题基础部分。

本部分内容主要是圆柱的认识以及侧面积、表面积的基本计算和应用，内容相对简单，多偏向于公式的运用，建议作为必须掌握内容进行讲解，一共划分为八个考点，欢迎使用。

【考点一】圆柱的认识。

【方法点拨】圆柱有三个部分组成，即底面、侧面、高：【典型例题1】下图中哪些是圆柱，在（）里打√，不是的打×。

( )( )( )( )( )( ) 解析：×√××√×【典型例题2】标出下面圆柱的底面、侧面和高。

(1) (2)（3）解析：(1)(2)(3)【典型例题3】圆柱体有上下两个底面，它们是完全相同的两个（），两底面之间的距离叫做圆柱的（）。

解析：圆；高【对应练习1】下面各图中h表示的是圆柱的高吗？是的在括号里画“√”，不是的画“×”。

( )( )( )( )( )解析：×；√；√；×；×【对应练习2】圆柱是由( )个面围成的。

圆柱的上、下两个面叫做( )。

圆柱周围的面（上、下底面除外）叫做( )。

圆柱的两个底面之间的距离叫做( )，圆柱有( )条高。

解析：3；底面；侧面；高；无数【对应练习3】从一个圆柱的上面和前面进行观察，看到的形状分别如图。

（1）这个圆柱的底面半径是________厘米，高是________厘米。

（2）这个圆柱应是下面的图________。

如何计算圆柱体与圆锥体的表面积圆柱体与圆锥体是常见的几何体，计算它们的表面积有一定的规律和公式。

本文将介绍如何计算圆柱体与圆锥体的表面积，并提供了详细的计算步骤。

1. 圆柱体表面积的计算方法圆柱体由一个底面和一个高度组成。

它的表面积由三部分构成：底面积、侧面积和顶面积。

1.1 底面积的计算圆柱体的底面为一个圆形，其半径为r。

底面积的计算公式为：底面积= π * (r^2)，其中π取近似值3.14159。

1.2 侧面积的计算圆柱体的侧面是一个圆的展开面，其形状为一个矩形。

矩形的长为圆柱体的高度h，宽为圆的周长，也就是2πr。

侧面积的计算公式为：侧面积= 2πrh。

1.3 顶面积的计算圆柱体的顶面与底面形状相同，所以顶面积也等于底面积。

因此，圆柱体的表面积等于底面积加上侧面积再加上顶面积：表面积= 2πr(r + h)。

2. 圆锥体表面积的计算方法圆锥体由一个底面和一个侧面组成。

它的表面积同样由三部分构成：底面积、侧面积和斜面积。

2.1 底面积的计算圆锥体的底面为一个圆形，其半径为r。

底面积的计算公式与圆柱体相同：底面积= π * (r^2)。

2.2 侧面积的计算圆锥体的侧面是由底面到顶点所形成的三角形。

这个三角形的周长为底面圆的周长，也就是2πr。

根据勾股定理可知，锥体的高为h，斜边为l。

根据勾股定理，l^2 = r^2 + h^2，所以斜边的长度l可以用sqrt(r^2 + h^2)表示。

侧面积的计算公式为：侧面积= πrl。

2.3 斜面积的计算圆锥体的斜面实际上就是侧面。

所以它的斜面积也等于侧面积。

综上所述，圆锥体的表面积等于底面积加上侧面积再加上斜面积：表面积= πr(r + l)。

3. 示例计算假设有一个圆柱体，其底面半径为3，高度为5。

首先计算底面积：底面积= π * (3^2) = 9π。

然后计算侧面积：侧面积= 2π * 3 * 5 = 30π。

最后计算表面积：表面积= 2 * 9π + 30π = 48π。

圆柱的侧面积公式圆柱是一种常见的几何形体，它由两个平行且相等的圆面和连接两个圆面的侧面组成。

在数学中，我们经常需要计算圆柱的各种属性，其中之一就是圆柱的侧面积。

圆柱的侧面积是指连接两个平行圆面的侧面的表面积。

为了计算圆柱的侧面积，我们需要知道圆柱的高度和半径。

圆柱的高度是指连接两个平行圆面的直线段的长度。

圆柱的半径是指圆柱的底面上任意一个圆的半径。

一旦我们知道了圆柱的半径和高度，我们就可以使用以下公式来计算圆柱的侧面积：侧面积= 2πr * h其中，π是一个数学常数，约等于3.14159。

r是圆柱的底面圆的半径，h是圆柱的高度。

这个公式的推导思路是，圆柱的侧面可以看做是一个展开的长方形，长方形的周长等于底面圆的周长，也就是2πr，高度就是圆柱的高度h。

所以，我们将长方形的周长乘以高度，就得到了圆柱的侧面积。

下面举一个例子来说明如何使用这个公式计算圆柱的侧面积：假设一个圆柱的底面圆的半径是5cm，高度是10cm。

我们可以将这些值代入公式，计算出圆柱的侧面积：侧面积 = 2 * 3.14159 * 5 * 10 = 314.159 平方厘米所以，这个圆柱的侧面积是314.159 平方厘米。

需要注意的是，圆柱的侧面积是一个二维的量，单位是平方长度单位，如平方厘米、平方米等。

它只描述了圆柱侧面的面积，而不包括圆柱的底面和顶面。

如果我们需要计算整个圆柱的表面积，应该将侧面积加上圆柱的两个底面积。

总结起来，计算圆柱的侧面积可以使用公式侧面积= 2πr * h，其中r是底面圆的半径，h是圆柱的高度。

将实际数值代入公式，即可计算出圆柱的侧面积。

这个公式在解决各种实际问题中非常有用，例如在建筑设计、工程计算和日常生活中都有广泛应用。

25. 立体图形的表面积知识要点梳理一、立体图形的切割1．立体图形每切割一次，增加两个面的面积。

2．立体图形每拼一次，减少两个面的面积。

二、表面积表面积：物体表面面积的总和叫做物体的表面积。

表面积通常用 S 表示，常用面积单位有平方千米、公顷、平方米、平方分米、平方厘米。

1．长方体、正方体的表面积为 6 个面的面积和。

2．圆柱的表面积＝侧面积＋2 个底面面积。

3．圆锥的表面积＝侧面积＋底面积三、立体图形的表面积计算公式考点精讲分析典例精讲考点1 长方体与正方体的表面积【例 1 】一个长 40 厘米，截面是正方形的长方体，如果长增加 5 厘米，表面积就增加80 平方厘米，原来长方体的表面积是多少？【精析】根据题意可知，一个长方体如果长增加 5 厘米，增加的80 平方厘米是 4个同样的长方形的面积和。

【答案】 80÷4÷5=4（厘米）0×4×4＋4×4×2＝672（平方厘米）答：原来长方体的表面积是672 平方厘米。

【归纳总结】根据长方体增加的面积，计算出长方体的宽和高，然后根据长方体的表面积计算公式解答即可。

【例2】学校新建一个游泳池，长50 米，宽 20 米，深 2 米。

这个游泳池占地面积有多大？如果游泳池的四壁和底面都要贴上瓷砖，一共需要贴多少平方米的瓷砖？【精析】此题主要考查长方体底面积及表面积的计算方法在实际生活中的应用。

解答时要清楚长方体游泳池的占地面积是指长方体的底面积。

贴瓷砖的面积，就等于游泳池的表面积减去上面的面积。

【答案】占地面积：50× 20＝ 1000（平方米）贴瓷砖的面积：（ 50× 2＋ 20× 2）×2＋50× 20＝ 1280（平方米）答：这个游泳池占地面积有1000 平方米，共需要贴1280 平方米的瓷砖。

【归纳总结】这类题目解答时一般遵循下列步骤：①识别形体；②搞清问题（求表面积还是求体积、容积、求表面积涉及几个面）；③回忆公式；④正确列式；⑤计算解答。

数学中很多同学对圆柱体积不知道如何计算，公式也不熟练，以下是由编辑为大家整理的“圆柱体积公式有哪些怎么算”，仅供参考，欢迎大家阅读。

圆柱体积公式1.π是圆周率，一般取3.14r是圆柱底面半径h为圆柱的高还可以是v=1/2ch×r侧面积的一半×半径2.圆柱体体积=底面积×高V=πR^2H=V=sh圆柱相关公式圆柱体积：V=底面积×高或V=1/2侧面积×高圆锥体积：V=底面积×高÷3圆柱侧面积：S侧=底面周长×高圆柱表面积：S表=侧面积+2个底面积字母表示：圆柱体积：V=sh圆锥体积：V=sh÷3圆柱侧面积：S=ch/2πrh/πdh圆柱表面积：s=ch+2πr2如何计算圆柱体积求圆基的半径。

两个圆都会做，因为它们大小相同。

如果你已经知道半径，你可以继续前进。

如果你不知道半径，那么你可以用尺子测量圆的最宽部分，然后除以2。

这将比测量直径的一半更准确。

我们说，这个圆筒的半径是1英寸(2.5厘米)。

把它写下来。

如果你知道这个圆的直径，就把它分成2个。

如果你知道周长，然后除以2π得到半径。

计算圆形基的面积。

要做到这一点，只是用公式求圆的面积，πR2=。

只要把你找到的半径插进去就可以了。

这里是如何做到这一点：aπx12==πx1。

因为π约3.14到三的数字，你可以说，圆形底座的面积是3.14。

2找到圆柱体的高度。

如果你已经知道高度了，继续前进。

如果没有，用尺子量一下。

高度是两个基棱之间的距离。

比方说，圆柱体的高度是4英寸(10.2厘米)。

把它写下来。

把基础的面积乘以高度。

你可以把圆柱体的体积看作是圆柱体的面积在圆柱的整个高度上延伸的体积。

因为你知道基的面积是3.14的2，高度是4，你可以把两者相乘，得到圆柱体的体积。

3.14英寸，2英寸，4英寸。

这是你最后的答案。

总是以立方单位陈述你的最终答案，因为体积是三维空间的量度。

六年级下册-打印版
圆柱侧面积计算公式的应用
应用一已知圆柱的底面周长和高，求圆柱的侧面积。

例一个圆柱，底面周长是3. 25 dm，高是1.6 dm，求它的侧面积。

分析知道圆柱的底面周长和高，直接根据公式S= Ch就可以求出圆柱的侧面积。

解答 3. 25×1.6=5. 2(dm²)
答：它的侧面积是5.2 dm2。

应用二已知圆柱的底面直径和高，求圆柱的侧面积。

例一个圆柱，底面直径是0.5 m，高是1.8 m，求它的侧面积。

（得数保留两位小数。

）分析先根据公式C=d求出圆柱的底面周长，再根据侧面积公式S=Ch进行计算，求出圆柱的侧面积，即S=dh。

解答 3. 14×0.5×1.8
=1. 57×1.8
≈2. 83(m2)
答：它的侧面积约是2. 83m2。

总结已知圆柱的底面直径和高，可以根据公式S=dh直接求出圆柱的侧面积。

应用三已知圆柱的底面半径和高，求圆柱的侧面积。

例计算右面圆柱的侧面积。

(单位：dm)
分析根据公式C= 2r先求出圆柱的底面周长，再根据公式S=Ch求出圆
柱的侧面积，即S=2rh。

解答：2×3. 14×5×15
=31.4×15
=471(dm2)
答：圆柱的侧面积是471 dm2。

总结已知圆柱的底面半径和高，可以根据公式S= 2 rh直接求出圆柱的侧面积。