当前位置：文档之家 › 交错等幅振荡函数

交错等幅振荡函数

  • 格式：pdf
  • 大小：115.28 KB
  • 文档页数：2

下载文档原格式

  / 2

合集下载

信号与系统第七章 系统函数

信号与系统第七章 系统函数

=
K
N1N 2 " N m e j(ψ1+ψ2 +"ψm ) M1 M2 " Mn ej(θ1+θ2 +"θn )
H (jω)
=
K
N1N2 " Nm M1M2 "Mn
ϕ (ω) = (ψ1 +ψ2 + "ψm ) − (θ1 +θ 2 + "θ n )
当ω 沿虚轴移动时，各复数因子(矢量)的模和辐角都
①H(z)在单位圆内的极点所对应的响应序列为衰减的。 即当k→∞时，响应均趋于0。 ②H(z)在单位圆上的一阶极点所对应的响应函数为稳 态响应。
③H(z)在单位圆上的高阶极点或单位圆外的极点，其 所对应的响应序列都是递增的。即当k→∞时，响应 均趋于∞。
第 19 页
三、由系统函数零、极点分布 决定频响特性
v1(t ) −
R
+
C v2(t )
−
写出网络转移函数表达式
H (s)
=
V2 (s) V1 (s )
=
1 RC
⎜⎛ ⋅⎜ ⎜⎜⎝
s
1 +1
RC
⎟⎞ ⎟ ⎟⎟⎠
=
1 RC
1 M1 ejθ1
= V2 ejϕ (ω) V1
M1
θ1
−1 RC
jω
O
σ
第 28 页
频响特性
jω
M1
V2 1 V1 1
2 θ1
−1 RC
O
σ
O1 RC
( ) H
jω
=
1 RC
1 M1 e jθ1
= V2 ejϕ (ω) V1

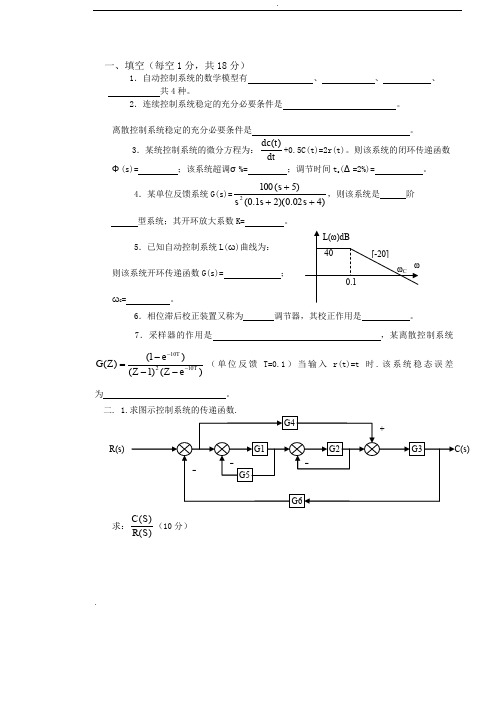
自动控制原理试题库20套和答案详细讲解

自动控制原理试题库20套和答案详细讲解

.一、填空（每空1分，共18分）1．自动控制系统的数学模型有 、 、 、共4种。

2．连续控制系统稳定的充分必要条件是 。

离散控制系统稳定的充分必要条件是 。

3．某统控制系统的微分方程为：dtt dc )(+0.5C(t)=2r(t)。

则该系统的闭环传递函数 Φ(s)= ；该系统超调σ%= ；调节时间t s (Δ=2%)= 。

4．某单位反馈系统G(s)=)402.0)(21.0()5(1002+++s s s s ，则该系统是 阶 型系统；其开环放大系数K= 。

5．已知自动控制系统L(ω)曲线为：则该系统开环传递函数G(s)= ；ωC = 。

6．相位滞后校正装置又称为 调节器，其校正作用是 。

7．采样器的作用是 ，某离散控制系统)()1()1()(10210T T e Z Z e Z G -----=（单位反馈T=0.1）当输入r(t)=t 时.该系统稳态误差为 。

二求：)()(S R S C （10分）R(s)2.求图示系统输出C（Z）的表达式。

（4分）四．反馈校正系统如图所示（12分）求：（1）K f=0时，系统的ξ，ωn和在单位斜坡输入下的稳态误差e ss.（2）若使系统ξ=0.707，k f应取何值？单位斜坡输入下e ss.=？..（1）（2）（3）五.已知某系统L（ω）曲线，（12分）（1）写出系统开环传递函数G（s）（2）求其相位裕度γ（3）欲使该系统成为三阶最佳系统.求其K=？，γmax=?六、已知控制系统开环频率特性曲线如图示。

P为开环右极点个数。

г为积分环节个数。

判别系统闭环后的稳定性。

.七、已知控制系统的传递函数为)1005.0)(105.0(10)(0++=s s s G 将其教正为二阶最佳系统，求校正装置的传递函数G 0（S ）。

（12分）一.填空题。

（10分）1.传递函数分母多项式的根，称为系统的2. 微分环节的传递函数为3.并联方框图的等效传递函数等于各并联传递函数之4.单位冲击函数信号的拉氏变换式5.系统开环传递函数中有一个积分环节则该系统为 型系统。

带通滤波器幅频相频分析

带通滤波器幅频相频分析
h(t)衰减
极点：
右半s平面→h(t)增长
一阶极点→h(t) 等幅振荡或阶跃
虚轴上
二阶极点→h(t) 呈增长形式
h(t)衰减
稳定系统（极点在左半s平面）
h(t)增长
如果在虚轴上→
非稳定系统（极点在右半s平面）
一阶：阶跃或等幅振荡（临界稳定）
二阶：以上不稳定系统
零极点分析
o
1.580
1.575
1.570
1.565 0
500
1000
1500
2000
系统的幅频、相频特性曲线
结论
当原件参数取合适值时为带通滤波 器，由传递函数看相当于一个高通 和一个低通滤波器串联
原件参数满足一定条件时可组成微 分电路、高通电路、积分电路、低 通电路或比例电路。
极点关系到系统的稳定性 零点影响系统冲激相应的幅值和相
位，不影响h(t)的形状。
h 2 ( t ) 1 [ H 2 ( s ) e ] t[c t o ss i t ] n e tA co t ) s(
其中： A 1()2, arctan
结论：H(s)的零点只影响h(t)的幅度和相位，而不影响形状。
系统的幅频、相频特性曲线
H (s)R 1(s s1/1)C 2(s 11/2)
-1/R1C1 -1/R2C2
H (s)R 1(s s1/1)C 2(s 11/2)
S平面上的负实轴的极点
H (s) 1 h(t) eatu(t) sa
冲激相应按指数规律衰减，为稳定的系统
H(s)零点的位置对系统的特性的影响
考虑如下两个系统：
H H2 1((ss)) ((ss s)s )2 2 2 2(s s h 1 )( 2 t ) 2 (1 s[H 1 ()s 2 ) ]e 2 tco ts

自动控制原理-第3章

自动控制原理-第3章

响应曲线如图3-2所示。图中
为输出的稳态值。
第三章 线性系统的时域分析 法
图 3-2 动态性能指标
第三章 线性系统的时域分析 法
动态性能指标通常有以下几种:
延迟时间td: 指响应曲线第一次达到稳态值的一半所需的时间
上升时间tr: 若阶跃响应不超过稳态值, 上升时间指响应曲线从 稳态值的10%上升到90%所需的时间; 对于有振荡的系统, 上升时 间定义为响应从零第一次上升到稳态值所需的时间。上升时间越 短, 响应速度越快。
可由下式确定: (3.8)
振荡次数N: 在0≤t≤ts内, 阶跃响应曲线穿越稳态值c(∞)次 一半称为振荡次数。
上述动态性能指标中, 常用的指标有tr、ts和σp。上升时间tr 价系统的响应速度; σp评价系统的运行平稳性或阻尼程度; ts是同
时反映响应速度和阻尼程度的综合性指标。 应当指出, 除简单的一 、二阶系统外, 要精确给出这些指标的解析表达式是很困难的。
中可以看出, 随着阻尼比ζ的减小, 阶跃响应的振荡程度加剧。 ζ =0时是等幅振荡, ζ≥1时是无振荡的单调上升曲线, 其中临界阻尼 对应的过渡过程时间最短。 在欠阻尼的状态下, 当0.4＜ζ＜0.8时过
渡过程时间比临界阻尼时更短, 而且振荡也不严重。 因此在 控制工程中, 除了那些不允许产生超调和振荡的情况外, 通常都希
第三章 线性系统的时域分析法 4. 脉冲函数 脉冲函数(见图3-1(d))的时域表达式为
(3.4)
式中,h称为脉冲宽度, 脉冲的面积为1。若对脉冲的宽度取趋于 零的极限, 则有
(3.5) 及
(3.6)
称此函数为理想脉冲函数, 又称δ函数(见图3-1(e))。
第三章 线性系统的时域分析 法

5-典型环节传递函数-振荡环节

5-典型环节传递函数-振荡环节
振荡环节(Oscillating Element)
2．传递函数与功能框
振荡环节的 功能框图阶跃响应振荡环节(Oscillating Element)
3．动态
当ξ=0时，c(t)为等幅自由振荡(又称为无阻尼振荡)。 其振荡频率为ωn，ωn称为无阻尼自然振荡 频率。
当0<ξ<1时，c(t)为减幅振荡(又称为阻尼振荡)。其振 荡频率为ωd, ωd称为阻尼自然振荡频率。
振荡环节(Oscillating Element)
4．举例
【实例1】 图为一RLC串联电路。若以 电源电压作为输入电压 ，以电容器两 端电压作为输出电压，此电路的传递 函数。并分析此为振荡电路的条件。 【解】 由基尔霍夫定律有
而流过电容的电流
其传递函数

自动控制原理第9章 习题及解析

自动控制原理第9章 习题及解析

第9章 习题参考答案9-1 设一阶非线性系统的微分方程为3x x x =-+试确定系统有几个平衡状态，分析各平衡状态的稳定性，并作出系统的相轨迹。

解 3x x x =-+由30x x -+=解得1230, 1, 1e e e x x x ===-。

作出系统的相轨迹图如下：平衡状态(0, 0)稳定，平衡状态(1, 0), (1, 0)-不稳定。

9-2 已知非线性系统的微分方程为(1) 320x x x ++= (2) 0x xx x ++= (3) 0x x x ++= (4) 2(1)0x x x x --+= 试确定系统的奇点及其类型，并概略绘制系统的相轨迹图。

解 (1) 奇点(0, 0)。

特征方程为2320λλ++=两个特征根为1,21, 2λ=--平衡点(0, 0)为稳定节点。

在奇点附近的概略相轨迹图：x(2) 奇点(0, 0)。

在平衡点(0, 0)的邻域内线性化，得到的线性化模型为0x x +=其特征方程为210λ+=两个特征根为1,2j λ=±平衡点(0, 0)为中心点。

在奇点附近的概略相轨迹图：x(3) 奇点(0, 0)。

原方程可改写为0000x x x x x x x x ++=≥⎧⎨+-=<⎩其特征方程、特征根和类型为21,221,2100.50.866 10 1.618, 0.618 j λλλλλλ⎧++==-±⎪⎨+-==-⎪⎩稳定焦点鞍点 在奇点附近的概略相轨迹图：(4) 奇点(0, 0)。

在平衡点(0, 0)的邻域内线性化，得到的线性化模型为x x x-+=其特征方程为210λλ-+=两个特征根为1,20.50.866jλ=±平衡点(0, 0)为不稳定焦点。

在奇点附近的概略相轨迹图：xx9-3 非线性系统的结构图如图9-48所示。

系统开始是静止的，输入信号r(t)＝4·1(t)，试写出开关线方程，确定奇点的位置和类型，在e-e平面上画出该系统的相平面图，并分析系统的运动特点。

二阶系统的传递函数


原点，其幅值越来越小，衰减越来越快；而另一个极点越来
越靠近原点，其幅值越来越大，衰减越来越慢。当阻尼比
ζ》1时，式右边最后一项可以忽略，二阶系统可以用靠近 原点的那个极点所表示的一阶系统来近似分析。
4. 系统阶跃响应的特点分析
①①响响应应特特性性 与与闭闭环环极极点点 位位置置有有关关
闭闭环环极极点点具具有有负负实实部部，，时时间间趋趋向向无无穷穷大大时时，， 瞬瞬态态响响应应趋趋于于零零，，系系统统稳稳定定。。
共共轭轭复复数数极极点点：：衰衰减减正正弦弦振振荡荡曲曲线线，，系系统统稳稳定定。。 负负实实数数极极点点：：响响应应是是单单调调上上升升曲曲线线，，系系统统稳稳定定。。 共共轭轭虚虚极极点点：：等等幅幅振振荡荡曲曲线线，，系系统统临临界界稳稳定定。。
②②响响应应的的快快慢慢与与极极点点 极极点点距距离离虚虚轴轴近近，，对对应应的的响响应应模模 距距离离虚虚轴轴的的远远近近有有关关 式式衰衰减减慢慢；；距距离离越越远远衰衰减减越越快快。。
（二） 二阶系统的阶跃响应
1. 二阶系统的传递函数
二阶系统结构如图
二阶系统闭环传递函数为
W (s) Y(s)
2 n
R(s) s 2 2 n s 2
二阶系统开环传递函数为
G(s)H (s)
2 n
s(s 2 n )
注注意意
典型环节与系统 的联系与区别
2. 二阶系统闭环极点的分布
根据系统阻尼比ζ的值，二阶系统有：
t 1 , w(t) 1 0.37
n n e
两个相同的负实数极点，两个相同的惯性环节的串联
④④过过阻阻尼尼系系统统
有两个负实数极点
y(t) 1
2 1 e s1

第5章 瞬态响应和稳态响应分析

2 ωn C ( s) = 2 2 R( s ) s + 2ζωn s + ωn
5.3 二阶系统
将标准闭环传递函数的特征方程进行因式分解， 将标准闭环传递函数的特征方程进行因式分解，得
ωn2 C (s) = R( s) s + ζωn + ωn ζ 2 − 1 s + ζωn − ωn ζ 2 − 1
3、一阶系统的单位脉冲响应 、
单位脉冲响应的函数的拉氏变换为： 单位脉冲响应的函数的拉氏变换为：
R( s) = 1
因此，有 因此，
C ( s) =
其拉氏反变换
1 Ts + 1
1 −t / T c(t ) = e T
），响应速度很大 当t=0时，系统有一个峰值很高的输出响应（脉冲），响应速度很大；然后输 时 系统有一个峰值很高的输出响应（脉冲），响应速度很大； 出响应迅速减小，响应速度也呈快速下降趋势； 出响应迅速减小，响应速度也呈快速下降趋势；当t= ∞ 时，系统输出响应趋近于 稳态值0。 稳态值 。
1 T T2 C (s) = 2 − + s s Ts + 1
c(t ) = t − T + Te −t / T
= r (t ) − c(t )
= T (1 − e − t / T )
误差信号函数： 误差信号函数： e(t )
表明： 表明：当t= ∞ 时，
因而， e− t / T = 0，因而，误差
ζ =1 ζ >1
（临界阻尼） 临界阻尼） （过阻尼） 过阻尼）
5.3 二阶系统
（1）欠阻尼情况（ 0 < ζ < 1 ） ）欠阻尼情况（
2 ωn C (s) = R( s) s + ζωn + ωn ζ 2 − 1 s + ζωn − ωn ζ 2 − 1

热工过程自动调节3

热工过程自动调节31调节量:即通过调节需要维持的物理量。

被调节对象：即被调节的生产设备或生产过程。

调节作用量:即在调节作用下，控制被调量变化的物理量。

2自动调节系统的分类：（1）按给定的信号的特点:恒值调节系统、程序调节系统、随机调节系统（2）按调节系统的结构分:反馈调节系统、前馈调节系统、复合调节系统。

（3）按调节系统闭环回路的数口分类:单回路调节系统、多回路调节系统。

（4）按调节作用的形式分:连续调节系统、离散调节系统。

（5）按系统的特性分:线性调节系统、非线性调节系统。

3反馈调节的特点（1）在调节结束时，可以使被调节量等于或接近于给定值，基于偏差的调节（2）在调节系统受到扰动作用时，必须等到被调量出现偏差后才开始调节，所以调节速度相对较慢。

前馈调节的特点：（1）由于扰动影响被调量的同时，调节器的调节作用已产生，所以调节速度响度较快。

基于扰动的调节（2）由于没有被调量的反馈，所以调节结束时不能保证被调量等于给定值。

4自动调节系统的性能指标：（1）稳定性（2）准确性（3）快速性5自动调节系统典型的调节过程:非周期调节过程、衰减振荡调节过程、等幅振荡调节过程、渐扩振荡调节过程6自动调节系统的数学模型:微分方程、传递函数、时间特性、频率特性7环节的基本连接方式:串联、并联、反馈连接8基本环节：比例环节、积分环节、惯性环节、微分环节、纯迟延环节。

各环节的特点：比例环节（响应非常及时），积分环节（响应比较缓慢），惯性环节（响应比较缓慢取决于时间常数T）,微分环节（超前响应），纯迟延环节（响应落后与输入信号）9热工对象存在的特性:输出量的变化过程是不振荡的，在扰动发生的开始阶段有迟延和惯性。

在过程的最后阶段，有自平衡能力的对象输出量达到新的稳态值P不为0,无自平衡能力的对象输出量不断变化，不能达到新的稳态值P为0。

10热工对象分为:有自平衡能力的对象（指对象在阶跃扰动作用下，不需要经过外加调节作用，对象经过一段时间后能自己稳定在一个新的平衡状态）；无自平衡能力的对象。

现代机械控制工程 第五章 系统的稳定性


其中，ai>0 (i=0,1,2,…,n)，即满足系统稳定的 必要条件。
劳斯稳定判据的判别过程如下：
n列出劳斯阵列 s a0 a2 sn-1 a1 a3 sn-2 b1 b2 sn-3 c1 c2 sn-4 d1 d2 …… s2 e1 e2 s1 f1 s0 g1
a1a2 a0a3 b1 a1 b2
K 0 6 5 K 0
即：当0<K<30时系统稳定。
例2：单位反馈系统的开环传递函数为：
K ( s 1) G( s) s(Ts 1)(5s 1)
求系统稳定时K和T的取值范围。 解：系统闭环特征方程为：
5Ts3 (5 T )s 2 (1 K )s K 0
系统稳定条件为：
T 0 K 0 (5 T )(1 K ) 5TK 0
T 0 5T 0 K 4T 5
劳斯阵列的特殊情况 劳斯阵列表某一行中的第一列元素等于 零，但其余各项不等于零或不全为零。 处理方法：用一个很小的正数 代替该行第 一列的零，并据此计算出阵列中的其余 各项。然后令 0，按前述方法进行判别。 如果零( )上下两项的符号相同，则系统存在 一对虚根，处于临界稳定状态；如果零 ( )上 下两项的符号不同，则表明有一 个符号变化，系统不稳定。
e t (a1 a2t ar t r 1)
当- < 0时，该输出分量指数单调衰减。 当- > 0时，该输出分量指数单调递增。 当- = 0时，该输出分量多项式递增。 对于一对r重复根-+j，相应的时域分量为：
e t (b1 b2t br t r 1 ) cos t (c1 c2t cr t r 1 ) sin t e t
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。