当前位置：文档之家 › 波函数与波动方程

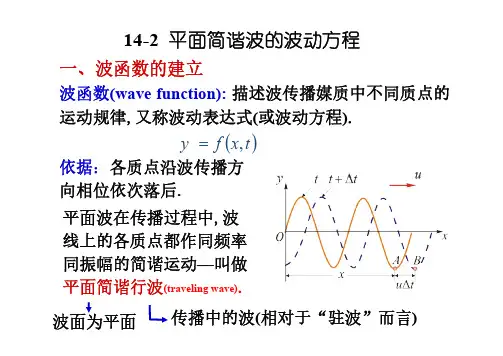
波函数与波动方程

  • 格式：ppt
  • 大小：18.96 MB
  • 文档页数：10

下载文档原格式

  / 10

合集下载

波函数的几种不同的形式

波函数的几种不同的形式

C、若 t 一定， E k 、 E p 随 x 周期分布。
D、能量以速度 u 传播。
二、波的能流（描述波的能量传播的物理量）：
1)能流 — 单位时间内垂直通过某一截面的能量。
设波速为u ，在 时t 间内通过垂直于波速截面
E u t S
的Su能量:
S
ε为截面所在位置的能量密度。
能流为：
ut
P E u S uS 2 A2 sin2[(t x )]
cos(t
20
2
r2 )
在 P 点的振动为同方向同频率振动的合成。
y1( p, ty2 ( p, t )
A2
cos(t
20
2
r2 )
由叠加原理P 点合振动：
y y1 y2 Acos(t )
A A12 A22 2 A1 A2 cos
( 20
干涉减弱
r2 r1
(2n 1)
2
n 0,1,2,3,...
[例1]在同一媒质中相距为20m 的两平面简谐波源S1 和S2 作同方
向,同频率(ν=100Hz )的谐振动,振幅均为A=0.05m,点S1 为波峰时,点S2恰为波谷,波速u = 200m / s 。
求：两波源连线上因干涉而静止的各点位置.
y2
Acos[2 (t
20
x)]
因干涉而静止的点的条件为:
[2 (t x 20 ) ] 2 (t x ) (2n 1)
n 0,1,2,
化简上式,得:
x n 10
2
将 u 代2入m,可得:
x n 10(m)
所以在两波源的连线上因干涉而静止的点的位置分别为:
x 1,2,3,,17,18,19m

波动方程或称波方程

波动方程或称波方程

波动方程或称波方程（英语：wave equation)是一种重要的偏微分方程，主要描述自然界中的各种的波动现象，包括横波和纵波，例如声波、光波、无线电波和水波。

波动方程抽象自声学、物理光学、电磁学、电动力学、流体力学等领域.历史上许多科学家，如达朗贝尔、欧拉、丹尼尔·伯努利和拉格朗日等在研究乐器等物体中的弦振动问题时,都对波动方程理论作出过重要贡献。

波动方程是双曲形偏微分方程的最典型代表，其最简形式可表示为：关于位置x 和时间t的标量函数u（代表各点偏离平衡位置的距离）满足：这里c通常是一个固定常数，代表波的传播速率。

在常压、20°C的空气中c为343米/秒（参见音速）.在弦振动问题中,c依不同弦的密度大小和轴向张力不同可能相差非常大.而在半环螺旋弹簧（一种玩具，英文商标为 Slinky)上,波速可以慢到1米/秒.在针对实际问题的波动方程中，一般都将波速表示成可随波的频率变化的量,这种处理对应真实物理世界中的色散现象。

此时，c应该用波的相速度代替：实际问题中对标准波动方程的另一修正是考虑波速随振幅的变化，修正后的方程变成下面的非线性波动方程：另需注意的是物体中的波可能是叠加在其他运动(譬如介质的平动，以气流中传播的声波为例）上的。

这种情况下，标量u的表达式将包含一个马赫因子（对沿流动方向传播的波为正，对反射波为负）。

三维波动方程描述了波在均匀各向同性弹性体中的传播。

绝大多数固体都是弹性体，所以波动方程对地球内部的地震波和用于检测固体材料中缺陷的超声波的传播能给出满意的描述。

在只考虑线性行为时，三维波动方程的形式比前面更为复杂,它必须同时考虑固体中的纵波和横波:式中：•和被称为弹性体的拉梅常数(也叫“拉梅模量”，英文Lamé constants 或 Lamé moduli)，是描述各向同性固体弹性性质的参数;•表示密度；•是源函数（即外界施加的激振力）；•表示位移；注意在上述方程中，激振力和位移都是矢量，所以该方程也被称为矢量形式的波动方程。

15-7波函数 玻恩统计解释

15-7波函数 玻恩统计解释

为了区别于经典波动，将上式写成：
( x, t ) 0e
i 2 (t x )
i (Et px)
0e
ψ0 e
第十五章
量子物理
1
物理学
第五版
15-7波函数 波函数物理意义
பைடு நூலகம்
玻恩统计解释
物质波与光波的对比
（波动观点） （微粒观点）
光波振幅平方大 光强大 光子在该处出现 的概率大
物理学
第五版
15-7波函数
玻恩统计解释
一、波函数（描写物质波的函数） 自由粒子的波函数 由波动理论，沿x轴传播的平面波波动方程：
y( x, t ) A cos 2 (t x )
y( x , t ) Ae
i 2 (t x )
只取实部
i 2 ( Et px ) h
2 2 势场中的一维运动粒子 E p i 2 2m x t
第十五章 量子物理
6
粒子在该处出现的 （微粒观点） 概率大 在空间某点波函数的平方和粒子在该点出现的 概率成正比. —玻恩统计解释.
第十五章 量子物理
2
物质波的 强度大
波函数振幅的平方大 （波动观点） | |2= *
物理学
第五版
15-7波函数
玻恩统计解释
物质波与经典波的本质区别
物质波是复函数，本身无具体的物理意义，
玻恩统计解释
一维自由粒子薛定谔方程 自由粒子波函数:
( x , t ) 0e
i ( Et px )
2 p2 2 2 x
非相对论粒子:
i E t
p2 E 2m

14-2平面简谐波的波动方程

14-2平面简谐波的波动方程

u
振动曲线 图形
A O
波形曲线
t A O t 0 P

t0 P
T

v
v
u x
研究 某质点位移随时间 对象 变化规律
由振动曲线可知
某时刻，波线上各质点 位移随位置变化规律
由波形曲线可知 该时刻各质点位移 波长 , 振幅A 只有t=0时刻波形才能提供初相
物理 周期 T 振幅 A 初相 0 意义
14-2 平面简谐波的波动方程
一、波函数的建立
波函数(wave function): 描述波传播媒质中不同质点的 运动规律,又称波动表达式(或波动方程).
y f x, t
依据：各质点沿波传播方 向相位依次落后. 平面波在传播过程中,波 线上的各质点都作同频率 同振幅的简谐运动—叫做 平面简谐行波(traveling wave). 波面为平面 传播中的波(相对于“驻波”而言)
x y A cos t u
(1)
P为任意点,波动表达式为
u O P( x )
x
方法2 波线上沿传播方向每走一个,相位落后2
P点相位比O落后
y P A cos(t
即
x

2π
x
y A cos(t
2π
P在 t=0 时刻过平衡位置向负向运动 ——波向左移
y(m)
0.2 O 1
t=0 P
2
yP(m) x(m)
0.2 O 0.1 0.2
t (s)
3 yO 0.2 cos(10πt π) 2 x 3 波向-x方向传播 y 0.2 cos[10 π(t ) π] 10 2 π π b) 以 P 为参考点 P yP 0 2cos( 10π t ) 2 2 波向-x方向传播 x 1 π 0 2 cos[10 π(t x ) π ] y 0 2 cos[10 π(t ) ] 10 2 10 2

波函数波动方程

波函数波动方程

量子力学中概率密度：p | ( x, t ) |2 * ( x, t )( x, t )
在量子力学中，可测量的函数f（x）的平均值：
f(x)=
L
0
* ( x) f ( x) ( x)dx

L
0
* ( x) ( x)dx
* ( x) f ( x) ( x)dx，
0
L
（若 = ( x, t )，意味着f(x)的测量值与时间有关）
动量的平均值
px *( x) px ( x)dx


( x)
坐标表象（representation） 用坐标（例如一维坐标系中的x）来表示物理体系 （物理量）的行为。
若存在p=p(x),与海森伯不确定关系违背，也与波粒 二象性违背。因此 px(x)是没有意义的，就无法用上 面的公式获得动量的平均值。


f (t )eit dt , 2 / T

傅立叶拟变换：f (t )
1 2


F ( )eit d
类比，可得到具有空间周期性的函数f(x)：
1 傅立叶变换：F (k ) 2


f ( x)eikx dx, k 2 /

1 傅立叶拟变换：f ( x) 2
ˆ xx) ˆ ˆ x ](x)=(xp ˆ ˆ x -p ˆ (x) [x,p d d x[i (x)] (i )[ x(x)] dx dx i (x)
ˆ xy) ˆ ˆ x ](x)=(yp ˆ ˆ x -p ˆ (x) [y,p d d y[i (x)] (i )[ y(x)] dx dx 0
ˆ ,L ˆ ]i [L 利用上关系式和角动量 x y 直角坐标分量算符的表达 [ L ˆ ,L ˆ ]i y z 式,也不难证明 ˆ ,L ˆ ]i [L z x

第2章 波函数与波动方程

第2章 波函数与波动方程

第2章波函数和薛定谔方程既然辐射和粒子都具有波动性和微粒性，那么，如何理解这两属性呢？它们如何统一起来？ 经典物理观点必须被修改。

主要表现：a. 波－粒两象性P （粒子） ν λ （波）ω=ν= h E （Planck 假设）Einstein 关系k P = （P h =λ，λπ=2k ） （de Broglie 假设） de Broglie 关系 ∴ 具有确定动量的自由粒子被一平面波所描述)Et r P (i )t r k (i AAe-⋅ω-⋅==ψb. 物理量取值不一定是连续的辐射体辐射的能量取值 ν=nh E ,2,1,0n = 氢原子的能量202n 8n a eE πε⋅-=cm 10529.0em 4a 82e 200-⋅=πε=由于平常粒子的波长1010-<λÅ，所以观察不到干涉, 衍射现象。

微观粒子，如电子1≈λÅ，因此在原子线度下可能显示出波动性。

而在宏观测量尺度下，几乎也不显示波动性。

将粒子所具有的微粒性和波动性统一起来，这在经典物理学中看来是不可能的，因经典粒子 经典波√原子性（整体性） ⨯实在物理量的空间分布 ⨯轨道 √干涉，衍射这两者是不相容的。

描述微观粒子既不能用经典粒子，也不能用经典波，当然也不能用经典粒子和经典波来描述。

§1 波函数的统计解释一、波函数的引入描述自由粒子可用平面波波函数)(Et r p ipAe -⋅=ψ来描述。

如果粒子处于随时间和位置变化的力场中运动，这样的微观粒子的运动状态也可以用较复杂的波(,)r t ψ完全描述。

二、波函数的解释1、经典物理学中粒子与波的有关概念经典概念中粒子意味着： 1.有一定质量、电荷等“颗粒性”的属性;2．有确定的运动轨道，每一时刻有一定位置和速度。

经典概念中波意味着：1. 某种实在的物理量的空间分布作周期性的变化; 2．干涉、衍射现象，即相干叠加性。

2、对波粒二象性的两种错误的看法 (1). 波由粒子组成波是由粒子组成的，把波看成是由大量粒子相互作用而在空间形成的一种疏密相间的周期分布。

4_2_2波动方程、波的能量、声波

引子： 引子：悬浮的小动物 究竟是什么力量使小 动物悬浮在空中的？ 动物悬浮在空中的？ 答案在本次讲课中。 答案在本次讲课中。
§2.4 波动方程与波速
一、波动方程 简谐波的波函数为： 简谐波的波函数为： y(x,t)=Acosk(ut-x) 2 y y = k 2u2 A sin k(ut x) = kuAsin k(ut x) 2 t t y 2 y = kAsin k(ut x) = k 2 A sin k(ut x) x x 2 2 2 y 2 y =u --- 平面波的波动方程 平面波的波动方程 2 2 t x 其通解为 y = f1 ( x + ut ) + f 2 ( x ut ) --- 平面波函数 平面波函数 u 为波速
w = w
k
W V
p
1 y = E 2 x
2
2
+ w
p
1 y 1 y = ρ + E t x 2 2
2
3.能量密度 能量密度 w = w
k
+ w
p
1 y 1 y = ρ + E t 2 2 x
E ρ
2
2
棒中纵波速度 u =
E = ρu 2
1 2 y w p = ρu 2 x
1 y = ρ t 2
2
2.势能密度 势能密度
--- 与弹性（形变）有关 与弹性（形变）
考虑一棒的线变， 考虑一棒的线变， 棒长： 截面： 棒长：l ，截面：S 两端拉力： 两端拉力：由0 → F 相应形变：增至 ， 应变。 相应形变：增至l，应力 ∝ 应变。
F ES l =E F= l = kl S l l 1 2 k (l ) 势能： W p = 势能： 2

02波函数与波动方程1


我们如何来理解这一点呢？因如果对一个体 系去测量发现粒子可能就处于 x1 ，只测得一个 值。 但可想像有很多很多同样的体系，对体系 进行同时，完全相同的测量，测得的结果发现 n1次 x1 x1 dx n2次 x2 x2 dx
nm次

xm xm dx

当对足够多的同样的体系进行测量后，即 在大量的完全相同的体系中，同时测量，那发 现粒子在 xi xi dx 处的几率
ni 2 ( x i , t ) dx nm
m
体系的波函数 (r, t ) 给出了体系所有信息 （可能范围内的），它给出体系一个完全的描述
例如，测量粒子的能量时，可给出预言可能测 得那些能量值和测得该能量值的几率等等。正 因为如此，我们可以说波函数描述了体系所处的 (r , t ) 描述体系，就称 量子状态，或称状态。以 (r , t ) 态，或称 (r , t ) 为体系的态函数。 体系处于
ei (k r t )
当然应该相等。因此，在任何条件下 (r, t ) 应连 续； 2 ② 有界：我们讲有界是指 (r, t ) dr 有界， 即使是在某些孤立奇点（对于 (r, t ) ）也可能不 违背波函数这一性质。只要在包含它的小区域中 的几率有界，实际上就是波函数平方可积。 例如： ，
B. 物质粒子波动性的实验证据 1. 戴维逊、革末实验（Davisson andGermer, P.R. 30(27) 707） 当可变电子束（30 600eV）照射到抛光的 镍单晶上，发现在某角度 方向有强的反射（即 有较多电子被接收），而 满足
a sin φn n h P
它证明了，电子入射到晶体表面，发生干涉散射， 具有波动性，而相应波长为

大学物理第二章 行波波动方程

应表示出所有质元在时刻 t 的位移，
除了取决 t o 外，
还应与质元的位置坐标有关
下面来写出平面简谐波的表达式
假设一平面简谐波在理想的、不吸收振动能量的 均匀无限大媒质中传播。
波传播的速度为 u ，方向如图 u
●
o
x
选择平行波线方向的直线为 x 轴。
u
●
o
x
在垂直 x 轴的平面上的各质元（振动状态相同），
即应变，则有
K 叫体变弹性模量,它由物质的性质决定,
“－”表示压强的增大总导致体积的减
§2.1 行波
一. 机械波的产生 1. 机械波产生的条件
振源 作机械振动的物体——波源 媒质 传播机械振动的物体 在物体内部传播的机械波，是靠物体的弹性形成的， 因此这样的媒质又称弹性媒质。
什么是物质的弹性？
机械振动是如何靠弹性来传播呢？
T
将上式改写


u

表明：波的频率等于单位时间内通过媒质 某一点的“完整波”的个数。
4. 波速 u
振动状态或振动位相的传播速度，也称相速度
波速的大小决定于媒质的性质，
(1) 固体中的横波
(2) 固体棒中的纵波
u
G

u E

G — 切变模量
E — 杨氏弹性模量 — 体密度
∵G < E, 固体中 ｕ横波 <ｕ纵波

a
2. 表达式也反映了波是振动状态的传播
y( x x，t t) y( x, t)
x ut
y
o●
u
t
ut
●
●
x
x x x
y Acos( t 2 x )

物理学14-平面简谐波的波函数与波动方程


若波源（原点）振动初位相不为零 y0 A cos( t 0 )
x y A cos[ (t ) 0 ] u
或
t x y A cos[ 2 ( ) 0 ] T 2x y A cos[ 2t ) 0 ] 2 y A cos[ (ut x) 0 ] A cos[ k (ut x) 0 ]
y
O
u
x
x
p
x O点振动状态传到p点需用 t u t 时刻p处质点的振动状态重复
y
O
u
x
x
p
x t 时刻O处质点的振动状态 u
x p点的振动方程： y A cos ( t ) u 沿x轴正向传播的平面简谐波的波动方程
沿着波传播方向，各质点的振动依次落后于波源振动 x 为p点的振动落后与原点振动的时间 u x 沿x轴负向传播的 y A cos ( t ) 平面简谐波的波动方程 u
在时间t内整个波形沿波的 传播方向平移了一段距离x
y
O
u
t
t t
x x
x
可见，波函数y(x,t)反映了波形的传播。 它描述的是在跑动的波，这种波被称为 行波（travelling wave）
三、平面波的波动微分方程
x y A cos[ ( t ) 0 ] u
求t 的二阶导数
2x0

若x0= 则 x0处质点落后于原点的位相为2
为x0处质点落后于原点的位相
是波在空间上的周期性的标志
同一波线上任意两点的振动位相差 x2 x1 x 2 1 2 2


பைடு நூலகம்
2、如果给定t，即t=t0 则y=y(x) Y x y A cos[ ( t 0 ) 0 ] u 表示给定时刻波线上各质 O 点在同一时刻的位移分布 ，即给定了t0 时刻的波形
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1.光电子的发射依赖于频率，而与光
强度无关。要有光电子发射，光频率就必
须大于某一值，即有一最低频率。
2.当照射光的频率
时m，in 发射出的
光电子动能大小与光强度无关，而仅与光
频率有关。
A. Einstein假设一束单色光由辐射能 量
大小为 的h量子组成，即假设光与物质
粒子交换能量时，是以“微粒”形式出现，
第一讲 回顾
Ⅰ. 辐射的微粒性 A. 黑体辐射 辐射本领：单位时间内，从辐射体
表面的单位面积上发射出的辐射能量的 频率分布，称为辐射本领，以 E(,T) 表示。 E(, T) 2 E(, T)
c
可以证明，辐射本领与辐射体的能量 密度的频率分布的关系为
E(, T) c u(, T) 4
(
u单(位, T为)
W(T)
u( , T)d
4 c
E( , T)d
45k 4 15h3
T4ቤተ መጻሕፍቲ ባይዱ
(
2 c3
)
W(T)
u( , T)d
4 c
E( , T)d
45k 4 15h3
T4
(
2 c3
)
可推出固体中原子振动能为
45k4 15h3
T4
(
2 v3T
1 v3L
)
固体低温下比定容热容 T3
C. 光电效应 当单色光照射到金属表面上，发现
)焦 耳 秒
米3
吸收率：照到物体上的辐射能量分布
吸收的份额,
A( 。, T)
G. Kirchhoff（基尔霍夫）证明，对 任何一个物体，辐射本领与吸收率之比
E(, T) A(, T) f (, T)
（ f (,T)与组成物体的物质无关）
EB(,T) f (,T)
1. 黑体的辐射本领 实验测得黑体辐射本领 的变化关系
这种 “微粒”带有能量 。 h
所以飞出电子的动能
Ek h w h( min ) 从而获得解释。
核心的问题是一束频率为 的单色
光，转移给一个电子的能量 E 除以频
率 为一常数
E 常数（h)
而这一常数与 ，光强度，电子及金属
材料无关。这一常数不能由经典物理学中 的常数给出。
D. 康普顿散射（ A. H. Compton ） 实验发现，单色 射X线与电子作用而 发生散射，其散射的 X 射线的波长为
动性外，在与物质的能量和动量的交换时
，还显示出微粒性（量子性），两者之间
的关系
E h
P E n h n h n k c c
h 6.626 1034焦耳 秒
1.054 1034焦耳 秒
Ⅱ. 原子结构的稳定性
A. 原子行星模型
卢瑟福（Rutherford）组用 粒子轰击原 子 发现， 粒子 以一定概率散射到
2c 4
kT（
Rayleigh–Jeans
）
应改为
E(, T)
2hc2 5
(ehc kT 1)
这就是普朗克 假设下的辐射本领 ，它与实验完全符 合。
① 当 kT hc （高频区）
E(, T)
2hc2 5
e hc
kT
Wein公式
当 kT hc （低频区）
E(,
T)
2c 4
kT
Rayleigh–Jeans公式
E与(,T)
在理论上
维恩（Wein）的辐射本领公式
E(, T)
C1 5
c e4 C2c
T
和瑞利―金斯（Rayleigh-Jeans）的辐
射本领公式
E(, T)
2c 4
kT
（ k为Boltzmann 常数：1.381023 焦）耳 K
这两个公式并不完全符合实验结果
2. 斯特藩－玻尔兹曼定律（StefanBoltzmann law）
R
(
1 n2
1) m2
R 3.2898 1015s1
C. Franch-Hertz实验 Franch-Hertz实验直接证明了汞原子
在4.9eV处存在量子化能级。
N.Bohr（尼.玻尔）提出三点假设： 1. 原子仅能稳定地处于与分立能量 （ E1,E2）,相对应的一系列定态中，不辐 射 能量； 2. 原子从一个定态到另一个定态时，
h 1）.0545 1034焦耳 秒
2
对于连续分布的辐射平均能量为
E EeE kTdE eE kTdE kT
0
0
而按 Planck 假设，辐射平均能量则为
E nh enh kT
enh kT
n0
n0
hc (ehc kT 1)
于是，用电动力学和统计力学导出的公式
E( , T)
也就是电子从一个轨道跃迁到另一轨道时 ，将吸收或发射电磁辐射，其辐射的能量 等于两定态的能量差，其频率为
是常数 3nR R 8.314焦，耳 但克分子 K
在低温下，其比定容热容是以 T3 0
普朗克（ M. Planck， 1900年）
普朗克假设：无论是 黑体辐射也好，还是
固体中原子振动也好， 它们都是以分立的能 量显示，即能量模式 是不连续的。
En nh n n 0,1,2,
（ h 6.626 1034焦耳 秒
s i A(1 cos )
A. Einstein 提出了 Einstein 关系
P E n h n h n c c
于是求得
s
i
h mec
(1
cos )
h 2.43 称10为12电m 子的康普顿波长
mec
从黑体辐射，固体低温比定容热容，光
电效应和康普顿散射的实验事实的讨论中
，我们可以得出结论：辐射除了显示其波
② Stefan-Boltznmann law
R(T) E(,T)d
25k4 15c2h3
T4
③ 维恩位移定律
由
E(, T)
2hc2 5
(ehc kT 1)
可得
hc (1 ehc kT ) 5 kT
于是
kT 0.2014 hc
0T0 0.2898 102 K m
④ 固体比定容热容 由辐射体的能量密度（ 焦耳 米3）
黑体辐射能量（单位时间，单位面积上
发射的能量）是与绝对温度 T成4正比
E(, T)d T4
（ 事实上，
）
3. 维恩位移定律 对于一确定的 T，0 相应地有一波长 ，0 使 E(0,T0达) 极大, 而
0T0 =常数 即
0T0 1T1 2T2
0.2898 102 K 米
B. 固体低温比定容热容 实验发现，在室温下固体比定容热容
大角度方向上。从而提出原子的行星模型 用这一模型计算散射微分截面，与实
验符合得非常好。
但是根据经典电动力学，带电粒子组成 的体系是不稳定的。原子应该坍塌。但事 实上，原子基态是稳定的。
B. 元素的线光谱，即有标志频率
h(n,m) 13.6eV( 1 1 ) n m（氢原子） n2 m2
(n,m)