波动方程和赫姆霍兹方程

亥姆霍兹涡量方程和亥姆霍兹波动方程
亥姆霍兹涡量方程和亥姆霍兹波动方程都是描述流体动力学的方程，但它们描述的是不同的物理量。

亥姆霍兹涡量方程（或涡旋运动方程）描述的是流体中涡旋的运动状态。

它是纳维-斯托克斯方程的一个变形，描述了在粘性流体中，由于流体粒子的运动和流体内部粘性力的作用，会形成涡旋，并使其发生运动。

这个方程的解可以用来描述涡旋的形状、大小、旋转速度等物理量的变化。

亥姆霍兹波动方程则描述的是流体中的压力分布。

它也是纳维-斯托克斯方程的一个变形，描述了在粘性流体中，由于流体粒子的运动和流体内部粘性力的作用，会形成压力波，并使其发生传播。

这个方程的解可以用来描述压力波的形状、速度、传播方向等物理量的变化。

总的来说，亥姆霍兹涡量方程和亥姆霍兹波动方程都是描述流体动力学中的涡旋和压力波的物理量及其变化的方程，但它们描述的是不同的物理量，因此在应用中需要根据具体的问题来选择使用哪个方程。

量子力学中的波动方程与亥姆霍兹方程量子力学是描述微观粒子行为的物理学理论，其核心是波动方程。

波动方程是描述波动现象的数学方程，而亥姆霍兹方程是波动方程的一种特殊形式。

本文将深入探讨量子力学中的波动方程与亥姆霍兹方程的关系和应用。

首先，我们来了解一下波动方程。

波动方程是描述波动现象的数学方程，它可以用来描述光、声波等各种波动现象。

在量子力学中，波动方程被应用于描述微观粒子的行为。

量子力学中的波动方程是薛定谔方程，它描述了微观粒子的波函数随时间和空间的变化。

薛定谔方程可以写成如下形式：Hψ = Eψ其中，H是哈密顿算符，ψ是波函数，E是能量。

薛定谔方程的解决了微观粒子的波函数，从而可以得到粒子的各种性质。

接下来，我们来了解一下亥姆霍兹方程。

亥姆霍兹方程是波动方程的一种特殊形式，它描述了平面波的传播。

亥姆霍兹方程可以写成如下形式：∇²ψ + k²ψ = 0其中，∇²是拉普拉斯算符，ψ是波函数，k是波数。

亥姆霍兹方程描述了波函数在空间中的传播和干涉。

在量子力学中，亥姆霍兹方程被应用于描述波函数的传播和干涉。

量子力学中的波函数具有波粒二象性，既可以看作是粒子的概率幅，又可以看作是波的传播。

亥姆霍兹方程描述了波函数的传播和干涉，从而可以解释一系列量子现象，如干涉、衍射等。

除了描述波函数的传播和干涉，亥姆霍兹方程还被应用于求解量子力学中的一些问题。

例如，在量子力学中，我们常常需要求解粒子在势场中的行为。

亥姆霍兹方程可以用来求解势场中的波函数，从而得到粒子的能量和态函数。

这对于研究微观粒子的行为和性质非常重要。

此外，亥姆霍兹方程还被应用于量子力学中的一些数值计算方法。

例如，有限差分法和有限元法等数值计算方法可以用来求解亥姆霍兹方程的近似解。

这些数值计算方法在量子力学的研究中扮演着重要的角色，可以帮助研究者更好地理解和探索量子世界。

总结起来，量子力学中的波动方程和亥姆霍兹方程是描述微观粒子行为的数学方程。

拉普拉斯方程泊松方程亥姆霍兹方程波动方程标题：深度解读拉普拉斯方程、泊松方程、亥姆霍兹方程和波动方程在数学和物理学领域中，拉普拉斯方程、泊松方程、亥姆霍兹方程和波动方程是一些重要的偏微分方程，它们在不同领域中扮演着重要的角色。

本文将从深度和广度的角度来探讨这些方程，并分析它们的意义和应用。

一、拉普拉斯方程1.1 拉普拉斯方程的定义拉普拉斯方程是一个偏微分方程，通常用Δu=0表示，其中Δ表示拉普拉斯算子，u是未知函数。

在数学物理学中，拉普拉斯方程是一个重要的调和方程，它描述了没有源项的稳态温度分布、电势分布或流体流动等物理现象。

1.2 拉普拉斯方程的应用拉普拉斯方程在电磁学、热传导、流体力学等领域有着广泛的应用。

通过求解拉普拉斯方程，可以得到电场、温度场和流速场等物理量的分布规律，从而为工程设计和科学研究提供重要的参考依据。

1.3 个人观点和理解对于拉普拉斯方程，我认为它在自然科学和工程领域中都具有重要意义。

通过深入理解和应用拉普拉斯方程，可以更好地理解和解释大量物理现象，为实际问题的求解提供了有力工具。

二、泊松方程2.1 泊松方程的定义泊松方程是一个偏微分方程，通常用Δu=f表示，其中Δ表示拉普拉斯算子，u是未知函数，f是已知函数。

泊松方程是拉普拉斯方程加上一个源项后得到的方程，它描述了包含源项的稳态温度分布、电势分布或流体流动等物理现象。

2.2 泊松方程的应用泊松方程在电磁学、热传导、流体力学等领域同样有着广泛的应用。

通过求解泊松方程，可以得到包含源项的电场、温度场和流速场等物理量的分布规律，从而更准确地反映实际问题的特性。

2.3 个人观点和理解对于泊松方程，我认为它在描述带有源项的物理现象时具有重要意义。

通过对泊松方程的深入理解和求解，可以更准确地预测现实世界中的电场、温度场和流速场等物理量分布规律，为工程设计和科学研究提供了有力工具。

三、亥姆霍兹方程3.1 亥姆霍兹方程的定义亥姆霍兹方程是一个偏微分方程，通常用Δu+k²u=0表示，其中Δ表示拉普拉斯算子，u是未知函数，k是已知常数。

亥姆霍兹方程（Helmholtz equation）是一条描述电磁波的椭圆偏微分方程，以德国物理学家亥姆霍亥姆霍兹兹的名字命名。

亥姆霍兹方程通常出现在涉及同时存在空间和时间依赖的偏微分方程的物理问题的研究中。

因为它和波动方程的关系，亥姆霍兹方程出现在物理学中电磁辐射、地震学和声学研究这样的领域里的问题中。

如：电磁场中的▽^2 E+k^2 E=0，▽^2 H+k^2 H=0，称为亥姆霍兹齐次方程，是在谐变场的情况下，E波和H波的波动方程。

其中：k^2=μω^2(ε-jσ/ω) 为波数，当忽略位移电流时，k^2=μεω^2；以上^2为平方。

相关书籍数学上具有(墷2+k2)ψ =f形式的双曲型偏微分方程。

式中墷2为拉普拉斯算子，在直角坐标系中为；ψ为待求函数;k2为常数；f为源函数。

当f等于零时称为齐次亥姆霍兹方程;f不等于零时称为非齐次亥姆霍兹方程。

在电磁学中，当函数随时间作简谐变动时,波动方程化为亥姆霍兹方程。

亥姆霍兹方程相关书籍亥姆霍兹方程亥姆霍兹方程相关书籍相关书籍。

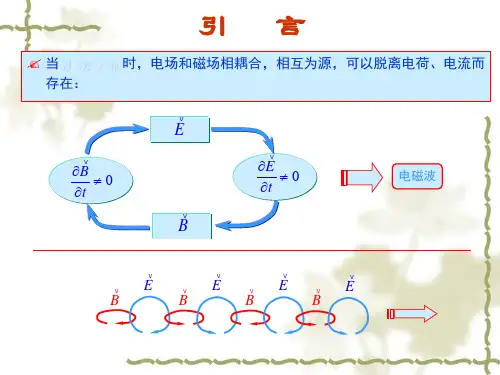
《电磁场与电磁波》（第四版）习题集：第4章时变电磁场第4章时变电磁场在时变的情况下，电场和磁场相互激励，在空间形成电磁波，时变电磁场的能量以电磁波的形式进行传播。

电磁场的波动方程描述了电磁场的波动性，本章首先对电磁场的波动方程进行讨论。

在时变电磁场的情况下，也可以引入辅助位函数来描述电磁场，使一些复杂问题的分析求解过程得以简化。

本章对时变电磁场的位函数及其微分方程进行了讨论。

电磁能量一如其它能量服从能量守恒原理，本章将讨论电磁场的能流和表征电磁场能量守恒关系的坡印廷定理。

本章在最后讨论了随时间按正弦函数变化的时变电磁场，这种时变电磁场称为时谐电磁场或正弦电磁场。

4. 1 波动方程由麦克斯韦方程可以建立电磁场的波动方程，揭示了时变电磁场的运动规律，即电磁场的波动性。

下面建立无源空间中电磁场的波动方程。

在无源空间中，电流密度和电荷密度处处为零，即0ρ=、0=J 。

在线性、各向同性的均匀媒质中，E 和H 满足的麦克斯韦方程为t ε=?EH （4.1.1） tμ=-?HE （4.1.2） 0?=H （4.1.3） 0?=E （4.1.4）对式（4.1.2）两边取旋度，有()()tμ=-E H 将式（4.1.1）代入上式，得到22()0t με+=?EE利用矢量恒等式2()()=??-?E E E 和式（4.1.4），可得到2220tμε??-=?EE （4.1.5）此式即为无源区域中电场强度矢量E 满足的波动方程。

同理可得到无源区域中磁场强度矢量H 满足的波动方程为2220tμε??-=?H H （4.1.6）无源区域中的E 或H 可以通过求解式（4.1.5）或式（4.1.6）的波动方程得到。

在直角坐标系中，波动方程可以分解为三个标量方程，每个方程中只含有一个场分量。

例如，式（4.1.5）可以分解为222222220x x x xE E E E x y z tμε++-= （4.1.7） 222222220yyyyE E E E x y z t με++-= （4.1.8）222222220z z z zE E E E x y z t με++-= （4.1.9）在其它坐标系中分解得到的三个标量方程都具有复杂的形式。

亥姆霍兹方程推导嘿，朋友！咱来聊聊亥姆霍兹方程的推导，这就像是一场奇妙的数学魔法之旅。

想象一下，你站在一个充满神秘符号和数字的迷宫前，这个迷宫就是物理学中的各种场和波动现象。

亥姆霍兹方程呢，就像是这个迷宫里隐藏的超级宝藏的地图。

咱们先从波动方程开始说起。

波动方程就像一个调皮的小精灵，跳来跳去的。

它描述着波的传播，就好像是在讲述一个关于水波如何在池塘里荡漾，或者声音如何在空气中传播的有趣故事。

波动方程大概长这样：∇²u = (1/c²) ∂²u/∂t²，这里的u就像是那个被波带着到处跑的小粒子，∇²就像是一个超级放大镜，在观察这个小粒子周围的情况，c呢，那就是波传播的速度，这个速度快得像闪电侠一样。

然后呢，我们假设这个波是一种特殊的波，就像一个有着固定发型的潮人，它是一种具有特定频率ω的时谐场。

这时候，我们就可以把u写成u(r,t) = A(r)e^(-iωt)，这就像是给这个波穿上了一件华丽的、带有特定风格的外套。

接着，我们把这个穿着华丽外套的表达式代入到波动方程里。

这就好比是把一个打扮奇特的人推进了那个神秘的迷宫里。

经过一番捣鼓，就像在迷宫里左拐右拐一样，我们就得到了亥姆霍兹方程：∇²A+ k²A = 0，这里的k = ω/c，这个k就像是这个迷宫里某个特殊区域的密码。

这个亥姆霍兹方程啊，它的意义可重大了。

它就像是一把万能钥匙，可以打开很多物理现象的大门。

比如说在电磁学里，就像打开了一个装满电磁魔法的宝箱，能帮助我们理解电磁场在特定情况下的分布，就像知道了小精灵在宝箱里的具体位置一样。

再看它的推导过程，就像是一场充满惊喜的冒险。

每一步的数学变换就像是在跨越一个又一个的小陷阱。

从波动方程到亥姆霍兹方程的转变，就像是把一个普通的故事变成了一个神秘的传说。

而且这个方程在声学里也超级有用。

如果把声音比作一群叽叽喳喳的小鸟，亥姆霍兹方程就能告诉我们这群小鸟在空间里是怎么分布着叽叽喳喳的，哪里声音大，哪里声音小。

一、介绍亥姆霍兹方程是描述波动现象的重要方程之一，在电动力学中也有着重要的应用。

本文将围绕亥姆霍兹方程推导波动方程在电动力学中的应用展开讨论，旨在深入探讨相关理论，并提供前沿的研究成果。

二、亥姆霍兹方程的基本原理1. 亥姆霍兹方程的概念及作用亥姆霍兹方程是描述波动现象的偏微分方程。

它是一种线性波动方程，能够描述一维波动现象，如声波、光波等。

亥姆霍兹方程也是电磁波方程中的一个重要组成部分，具有广泛的应用价值。

2. 亥姆霍兹方程的数学表示亥姆霍兹方程可用数学符号表示为△u+k²u=0，其中△为拉普拉斯算子，u为波函数，k为波数。

该方程是一个关于波函数u的二阶偏微分方程，描述了波在空间中的传播过程。

三、亥姆霍兹方程在电动力学中的应用1. 电磁波方程的推导电磁波是由电场和磁场相互作用形成的波动现象，其传播过程可由亥姆霍兹方程描述。

通过麦克斯韦方程和波动方程的推导，可以得到描述电磁波传播的波动方程，从而揭示了电磁波的性质和特点。

2. 电磁波的传播特性利用亥姆霍兹方程可以研究电磁波的传播特性，如波速、频率、偏振等。

通过对波动方程的分析和求解，可以深入了解电磁波在空间中的传播规律，为相关技术和应用提供理论依据。

3. 电磁波在介质中的传播介质对电磁波的传播具有影响，利用亥姆霍兹方程可以研究介质中电磁波的传播性质。

介质的介电常数和磁导率对电磁波的传播速度和衰减效应有重要影响，因此通过亥姆霍兹方程可进行相关研究和分析。

四、前沿研究与应用1. 亥姆霍兹方程的数值模拟随着计算机技术的发展，利用亥姆霍兹方程进行电磁波传播的数值模拟成为研究的热点。

采用有限差分、有限元等方法，可以对电磁波在复杂介质和结构中的传播进行模拟和分析，为相关领域的工程设计和优化提供支持。

2. 电磁波的控制与调制利用亥姆霍兹方程可以研究电磁波的控制和调制技术。

通过改变波函数的边界条件、介质特性等方式，可以实现对电磁波的传播和辐射特性的调控，为通信、雷达、遥感等领域的应用提供新的思路和方法。

声场亥姆霍兹方程一、亥姆霍兹方程的引出（一）波动方程在声学中，对于小振幅声波的传播，在均匀的、静止的理想流体介质中，声波的波动方程为：∇^2p - (1)/(c^2)frac{∂^2p}{∂ t^2} = 0其中p是声压，∇^2是拉普拉斯算符，c是声速，t是时间。

（二）时谐声波假设当考虑时谐声波（即声波随时间作简谐变化）时，设p(→r,t)=P(→r)e^-iω t，这里→r是空间位置矢量，ω = 2π f是角频率，f是频率，P(→r)是仅与空间位置有关的复声压幅值。

将p(→r,t)=P(→r)e^-iω t代入波动方程∇^2p - (1)/(c^2)frac{∂^2p}{∂ t^2} = 0，可得：∇^2(P(→r)e^-iω t)-(1)/(c^2)frac{∂^2(P(→r)e^-iω t)}{∂ t^2} = 0由于(∂)/(∂ t)(e^-iω t)=-iω e^-iω t，frac{∂^2}{∂ t^2}(e^-iω t)=-ω^2e^-iωt方程变为：e^-iω t∇^2P(→r)+frac{ω^2}{c^2}P(→r)e^-iω t= 0两边同时消去e^-iω t，就得到了亥姆霍兹方程：∇^2P(→r)+k^2P(→r) = 0，其中k = (ω)/(c)称为波数。

二、亥姆霍兹方程在声场中的物理意义（一）描述稳态声场亥姆霍兹方程描述的是稳态（时谐）声场中声压幅值P(→r)的空间分布规律。

它反映了在给定频率ω下，声波在空间中的传播和分布特性，与声源的特性、传播介质的性质以及边界条件等因素密切相关。

（二）与能量分布的联系在声场中，声能量密度与声压的平方成正比。

亥姆霍兹方程通过确定声压幅值的分布，间接地反映了声场中能量的分布情况。

例如，在亥姆霍兹方程的解中，声压幅值较大的区域通常对应着较高的声能量密度区域，这有助于我们理解声波在空间中的聚焦、散射等能量相关的现象。

三、求解亥姆霍兹方程（一）分离变量法1. 直角坐标系下- 对于直角坐标系(x,y,z)，设P(x,y,z)=X(x)Y(y)Z(z)，将其代入亥姆霍兹方程∇^2P + k^2P = 0，其中∇^2=frac{∂^2}{∂ x^2}+frac{∂^2}{∂ y^2}+frac{∂^2}{∂z^2}。