a
2k 1
nm
极点之和减去 零点之和。
k依 次 取0, 1, 2,一 直
到 获得n m个 倾角 为 止。
例1、某单位反馈系统的开环传递函数为
Gs
ss
K
1s
2
开环有三个极点 p1 0, p2 1, p3 2
开环无零点
n 3, m 0, 故三条根轨迹趋向处。
渐进线与实轴交点的坐标为
[S]
Apj s pj
pj s pj
i 1,2,m j 1,2,n
因此有:幅角条件
m
n
zi pj 180 2k 1
i 1
j 1
k 0,1,2,
m
Azi
幅值条件
K
i 1 n
1
Apj
j 1
可见,幅角条件与K 无关;
而幅值条件与K 有关,且K 由0 ~ 。
因 此 , 复 平 面[ S ]上 所 有 满 足 幅 角 条 件 的点 都 是
零点,另外n m条根轨迹趋向于何处呢?
n m,且K
s z1 s s p1 s
z2 s zm p2 s pn
1 K
0
只有当s 时,上式可写为:
sm sn 0
即1 snm
0
s
当 K 时,有n m条根轨迹趋于无穷远处。
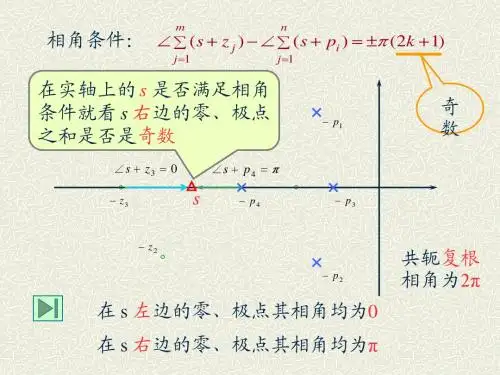
四、实轴上的根轨迹
实轴上根轨迹区段的右侧,开环零点、极点数目之和应为奇 数。
K
1
M
s s2
K 1s
[S]
K s s2
1 j 1 j 2
-2
0
1 j 1 j 2 2 2
K
N
K 1 2
4.2 绘制根轨迹的基本法则