当前位置：文档之家 › 第四章根轨迹分析法

第四章根轨迹分析法

  • 格式：pdf
  • 大小：549.28 KB
  • 文档页数：73

下载文档原格式

  / 73

合集下载

自动控制原理-第4章 根轨迹

自动控制原理-第4章 根轨迹

又 ∵ 根轨迹方程
n
n
(spi) sn( pi)sn 1L
n
m
Kim 1
i 1 m
snm( pi zj)snm 1L
(szj) sm( zj)sm 1L
i 1
j 1
j 1
j 1
n
m
∴ sn-m-1项系数对应相等
(nm)(a) pi zj
n
m
i1
j1
(2k 1) ,
nm
pi zi
闭环零、极点与开环零、极点的关系
闭环传递函数 (s) G(s)
1G(s)H(s)
开环传递函数 Gk(s)G(s)H(s)
f
l
(s zi)
(s z j)
G (s) KG
i 1 q
H
(s)
K
H
j 1 h
(s pi)
(s p j)
i 1
j 1
f
l
(szi)(szj)
Gk(s)G(s)H(s)K
如何应用根轨迹方程在[s]平面上找到闭环极点。
解： G ( s ) K 0 .5 K K * s(2 s 1) s(s 0.5) s(s 0.5)
K * 0.5 K 开 环 极 点 p1 0， p2 0.5 无开环零点 根据相角方程
s2
p2 4 5 o -0.5 s1
135o
p1 0
m
(s z j)
K j1 n
1
(s pi)
i1
m
n
(szj) (spi)(2k1)
j1
i1
k0,1,2,L
（1）相角条件是决定闭环根轨迹的充要条件； 在测量相角时，规定以逆

自动控制原理(胡寿松版)课件第四章

自动控制原理(胡寿松版)课件第四章

第一节 根轨迹的基本概念
二、根轨迹与系统性能
根轨迹图可以分析系统的各种性能： ω j ∞ ↑ 稳定性: 根轨迹均在s的左半平 Kr 面，则系统对所有k>0的值是稳定的。 s K =0 1 1 s1 2 r 0 σ -1 稳态性能：如图有一个开环极点 -2 -1 s=0，说明属于I型系统，阶跃作用 Kr ∞ 下的稳态误差为0。 动态性能：过阻尼 临界阻尼 欠阻 尼。 K越大，阻尼比 越小，超调量σ%越大。
第四章 根轨迹分析法
第一节 根轨迹的基本概念
当系统的某个参数变化时，特征方程的根随 之在S平面上移动，系统的性能也跟着变化。研究 S 平面上根的位置随参数变化的规律及其与系统 性能的关系是根轨迹分析法的主要内容。
第一节 根轨迹的基本概念
一、根轨迹
设系统的结构如图 K r变化时,闭环特征 Kr 根在 s平面上的轨迹 : 极点；右半平面为 C(s) 2+2s+K s1 s2 Kr 不稳定极点；虚轴 R(s) =s∞ ω r j ↑ -2 0 0 上为临界极点。 闭环特征方程式 Kr 1 -1 -1 1 2 (2) 0<Kr<1时，系统 s 0 s2 +2s+K Kr=0 1r= s1 -1-j -1+j 2 0 σ -1 有呈过阻尼状态。 -2 特征方程的根 -1 -1+j∞ -1-j∞ Kr (3) 当 时，系统 ∞Kr=1 s1.2 =-1± 1-Kr ∞ 呈临界阻尼状态 。 得相应的闭环特征根值: (4) 1<Kr<∞时，系统呈欠阻尼状态。
↑
↑
第一节 根轨迹的基本概念
三、闭环零、极点与开环零、极点的关系
系统传递函数为
G( s) ( s) 1 G(s) H (s)

自动控制原理第四章-根轨迹分析法

自动控制原理第四章-根轨迹分析法
jω
×
p4 z 2
×
p3
×
×
p 2 z1 p1
σ
规则4：根轨迹的分会点（分离点和会合点）d。 （1）定义：分会点是指根轨迹离开实轴进入复平面的点（分 离点）或由复平面进入实轴的点（汇合点），位于相邻两极点 或两零点之间。
（2）位置：大部分的分会点在实轴上，若出现在复平面内时，则 成对出现。
（3）特点：分会点对应于闭环特征方程有重根的点；根轨迹离开
（4）与虚轴的交点：
方法1：闭环特征方程为s3 + 6s2 + 8s + K*= 0 令s = jω得：-jω3 -6ω2 + j8ω + K* = 0
-6ω2 + K* = 0 即
-ω3 + 8ω= 0
K* = 48 ω= 2.8 s-1
方法2：闭环特征方程为 s3 + 6s2 + 8s + K*= 0 列劳斯表如下：
规则1：根轨迹的起点和终点。 根轨迹起始于开环极点，终止开环零点或无穷远。
m
i 1
s
zi
n
s
l 1
pl
1 K
K
K
0 s pl
s s
zi , m条 （, n
m）条
规则2: 根轨迹的条数和对称性。 n阶系统有n条根轨迹。根轨迹关于实轴对称。
规则3: 实轴上的根轨迹分布。
由实数开环零、极点将实轴分为若干段，如某段右边 开环零、极点（包括该段的端点）数之和为奇数，则该段就 是根轨迹，否则不是。如下图所示。
又因为开环传函的零极点表达式为：
m
GK (s)
G(s)H(s)
K
n
(s

第四章控制系统的根轨迹分析法

第四章控制系统的根轨迹分析法
○
− p4
− p3
∠s + z 2
∠s + p2
− p2
共轭复根 相; ∠s + p2 = 2π 在 s 左边的零、极点其相角均为0
∠s + z1 + ∠s + z2 = 2π 在 s 右边的零、极点其相角均为π
n m 0 出射角公式： 出射角公式： θ pc =180 + ∑θzj − ∑θ pi j =1 i=1
ζ = 0.707
s’ s’
-2 0
K −1
Re
-1
根轨迹法的分析基本思路: 根轨迹法的分析基本思路 目的: 目的
①解决高阶系统求解特征根比较困难 的实现; 寻找到一种方便、 的实现 ②寻找到一种方便、有效的描述 系统的根轨迹的方法。 系统的根轨迹的方法。
方法: 方法
① 根据开环零极点的分布绘制出系统 的根轨迹图； 的根轨迹图；②利用根轨迹法来分析和设 计系统. 计系统
S1
0 -1 -1+j -1+j∞
∞ ↑ K
S2
-2 -1 -1-j -1-j∞ jω
1 S1 0 σ -1
闭环特征方程式 S2+2S+K= 0
S2 -2
特征方程的根 S1.2 = -1± 1-K ±
K变化时,闭环特征根 变化时,
在S平面上的轨迹图形
-1 K ∞ ↑
系统特征方程为 求得两个极点： 求得两个极点：
jω
z1 p3 -2 p2 -1 z2 1 p
1 0
-1
3、实轴上的根轨迹 、
实轴上某区间存在根轨迹， 实轴上某区间存在根轨迹，则 该区间右边的开环零、 该区间右边的开环零、极点数之和 必为奇数。 必为奇数。

第4章 根轨迹法

第4章 根轨迹法
i =1
m n
sk
s+
jω
s+p
s
j=1 n
=
1 ； K gk
−z j
z
j
i
αj
βi
σ
0
∑ α jk − ∑ βik = ±180 (1 + 2k) (k = 1, 2,⋯)
j=1 i =1
−p i
幅值条件为：
∏ s + zj ∏ s + pi
i =1 j=1 n
m
1 = Kg
幅角条件：
∑ α j − ∑ βi = ±180 (1 + 2k)
j=1 i =1
m
n
(k = 1, 2,⋯)
三、应用幅值条件确定 K g 值
jω
△
某控制系统的开环传递函数为
1 K g (s + ) K(8s + 1) 8 G(s)H(s) = 2 = s (2s + 1) s 2 (s + 1 ) 2
-0.5 L3
sk L 1,2 l 60° σ
1 8 1 p1 = − 2 z1 = −
可见，闭环零点由前向通道的零点和反馈通道的极点组成， 闭环零极点放大系数等于前向通道零极点放大系数 K Gg 。
一、根轨迹的连续性 第二节 绘制根轨迹的一般规则 二、根轨迹的分支数 三、根轨迹的对称性 四、根轨迹的起点和终点
m m
j=1 lim n s→∞ i =1
∏ s + zj ∏ s + pi
六、根轨迹的分离点和会合点
D(s) K g (s) = − N(s)
dK g (s) ds
=0
D' (s)N(s) − N ' (s)D(s) = 0

第四章 控制系统根轨迹分析法

第四章 控制系统根轨迹分析法
i j 1 j
4.1 根轨迹的概念
模条件与角条件的作用： 1、角条件与k无关，即s平面上所有满足角条件的 点都属于根轨迹。（所以绘制根轨迹只要依据角条 件就足够了）。 2、模条件主要用来确定根轨迹上各点对应的根轨 I 迹增益k值。
m
k

j 1 m
n
s p
j
s Zi
args Z i
1
所以结论：实轴上线段右侧的零、极点数目之和为奇 数时，此区段为根轨迹。
jω
例
k G0 ( s ) Ts 1
1 T
×
×
×
×
σ
1 p T
j


1 1 T F 1 T 2k 1 1
k' G0 ( s ) s( s 0.5 )
j
p1 0 p2 0.5
k G0 s 举例： 开环传函： ss 1
K为开环增益（因为标准型） 有两个开环极点 无开环零点
rs
k ss 1
C s
k G s 2 闭环传函： s sk
2 D s s sk 0 则闭环特征方程为：
1 1 闭环特征根（即闭环传函的极点）： s1 1 4k
0 0 .5 F 0.25 2 2k 1 3 , 2 2 2

-0.5 0
4.2 根轨迹的绘制规则
规则四：根轨迹的渐近线： （1）条数： （n-m）条 （2）与实轴所成角度 当
m n 2k 1
n m
s 时，认为所有开环零极点引向s的角相同
Z1 Z m p1 p n
G 0 s k
m
为m个开环零点

根轨迹分析法

根轨迹分析法

在极点0和极点-1之间的根轨迹上一定有分离点存在， 令d[G(s)H(s)]/ds＝0，整理后求得s1= -0.42（在根轨迹上， 是分离点），s2 = -1.58 （不在根轨迹上，舍），所对应K* 由幅值条件确定：
K1* s1 s1 1 s1 2 0.42 0.581.58 0.38 用劳斯判据法与虚轴交点：
s 3 3s 2 2s K * 0
s3 s2 s
1
1 3 6 K* 0 3 K*
2 K*
3s 2 6 0
K* 6 s j 2
自动控制原理
12
s0
(8)根轨迹的出射角和入射角
（8）根轨迹的入射角和出射角 出射角：根轨迹离开开环复数极点处的切线方向与正实 轴之间的夹角 入射角：根轨迹进入开环复数零点处的切线方向与正实 轴之间的夹角 结论：开环复数极、零点的出射角与入射角由下面公式 计算 出射角： p 180 ( s zi ) ( s p j )
j 1
n
j
K
*
sz
i 1
m
i
0
当K* →0时， s→pj (j=1，2，…，n)为系统的开环极点； 当K*→∞时，s→zi (i=1，2，…，m)为系统的开环零点。 结论：根轨迹起始于开环极点，终止于开环零点。如果开环 零点数目m小于开环极点数目n，则有n-m条根轨迹终止于无 穷远处。
令K从0到∞变化，则闭环特征根在复 平面上描绘出若干曲线（根轨迹）。
自动控制原理
4
4.2
根轨迹的概念（续）
（2）从根轨迹图分析闭环系统各种性能 分析稳定性：在0<K<∞范围内，系统是稳定的。 分析动态性能：当0<K<0.5时，系统是过阻尼的； 当K=0.5时，系统为临界阻尼状态； 当K>0.5时，系统是欠阻尼的。 若已知K=1，则闭环极点为-1±j，参数ζ=0.707， ω=0.414，系统的瞬态响应指标超调量σ%= 4.3%，调节 时间ts＝3秒。 当K继续增大时，其超调量σ%将增大，而调节时 间基本不变。 分析稳态性能：系统是Ⅰ型的，阶跃函数作用下的稳态误 差为零。

第4章 根轨迹

第4章 根轨迹

m
(s p
j 1
n
1
j
)
因ｓ为复变量，根轨迹方程又可分解为幅值方程和相 角方程。 幅值方程为
K r (s zi )
i 1 m
(s p
j 1
n
1 或
(s z )
i
m
j
)
(s p
j 1
i 1 n
j
)
1 Kr
相角方程为
(s z ) (s p ) (2k 1)
设p3的出射角为θ3，如图所示。
假设s1为根轨迹上的一点，则s1应 满足相角方程
(s
i 1
1
1
z i ) ( s1 p j ) (2k 1)
j 1
4
由此可推得出射角的一般表达式
l ( pl zi ) ( pl p j ) i j
例4-6 已知系统的开环传递函数为
K r (s 1.5)(s 2 4s 5) G( s) H ( s) s(s 2.5)(s 2 s 1.5)
试绘制系统的根轨迹图。
18
7. 根轨迹与虚轴的交点
根轨迹与虚轴的交点是系统稳定与不稳定的分界点，常 常需要求得这一交点和相应的Kr值。 设与虚轴相交的闭环极点为ｓ=jω，代入闭环特征方程得：
根为两个复数根，系统呈欠阻尼 状态，即输出呈衰减振荡形式。 特征根的实部σ为衰减系数，虚 部ω为振荡频率。
4
4.1.2 根轨迹方程
设系统的结构如图所示。 系统的闭环传递函数为
C ( s) G(s) R( s ) 1 G ( s ) H ( s )
开环传递函数的一般表达式为

第四章根轨迹分析法1244页PPT

第四章根轨迹分析法1244页PPT
方程的根的变化。
例4-1 系统结构图如图所示，分析l 随开环放大系 数K变化的趋势。
解. G(s) K Kg
s(0.5s1) s(s2)
K : 开环放大系数
Kg 2K: 根轨迹增益
(s)C(s) Kg R(s) s22sKg
D (s)s22sKg0
l1,2 1 1Kg
Kg l1 l2
2.根轨迹方程
j 1
则根轨迹的条件方程为 幅值条件
m
(s zi )
K i1 gn
1
(s p j )
j 1
m
argK[g
(szi
i1
)
]180(2k1)
n
(spj )
j 1
方程
相角条 件方程
m
n
ars g zi)( ars gpj( ) 1 8 (2 k 0 1 )
i 1
j 1
注意：
相角条件是确定根轨迹的充分而必要条件 可从幅值条件方程求解得出Kg 。
解：
j 平面
-4
-1.5 -1 -0.5 0
取实轴上的点s
开环共轭极（零点）对相角条件无影响
j
[s]
p3
p1
z2 p5 s p2
z1 0
p4
实轴上的根轨迹仅由实轴上的开环零极点的分 布所决定
6. 根轨迹的渐近线 若 n>m，则 Kg 时，有n-m条根轨迹
k g= 0 .2 5 kg= 0
-1 -0 .5
k g= 0 .5
j
s1,2
1 2
1 2
s平面
1 4Kg
0 kg= 0
系统的开环传递函数中某一参数变化时，系统闭 环特征方程的根在S平面上的变化轨迹即为根轨迹

自动控制原理第四章根轨迹法(管理PPT)

自动控制原理第四章根轨迹法(管理PPT)

根轨迹法的优化建议
结合其他方法
将根轨迹法与其他分析方 法（如频率响应法）相结 合，以获得更全面的系统 性能分析。
ቤተ መጻሕፍቲ ባይዱ开发软件工具
开发专门用于根轨迹分析 的软件工具，以提高分析 的效率和准确性。
加强实践应用
在实际工程中加强根轨迹 法的应用，通过实践不断 优化和完善该方法。
05
CATALOGUE
根轨迹法与其他控制方法的比较
根轨迹分析的实例
假设一个开环传递函数为 G(s)H(s) = (s+1)(s+2)/(s^2+2s+5)，对其进行 根轨迹分析。
分析根轨迹图，确定系统的稳定性、 动态性能和系统参数的影响。
根据开环传递函数，绘制出根轨迹图 ，并标注出系统的极点和零点。
根据根轨迹图进行系统设计和优化， 例如调整开环传递函数的增益参数， 以改善系统的性能。
对于非线性系统，根轨迹法可能无法给出准确的描述和分析。
04
CATALOGUE
根轨迹法的改进与优化
根轨迹法的局限性与挑战
参数敏感性
根轨迹法对系统参数的微小变化非常敏感，可能导致根轨迹的剧 烈变化，影响系统的稳定性。
无法处理非线性系统
根轨迹法主要适用于线性系统，对于非线性系统的分析存在局限性 。
计算复杂度较高
和设计。
对于具有特定性能指标要求的系统，如 快速响应、低超调量等，可以根据系统 特性和性能要求选择适合的控制方法，
如状态反馈控制器等。
06
CATALOGUE
根轨迹法的实际应用案例
根轨迹法在工业控制系统中的应用
根轨迹法在工业控制系统中广泛应用于系统的分析和设计。通过绘制根轨迹图，可以直观地 了解系统性能的变化，如稳定性、响应速度和超调量等。

《自动控制原理》第4章_根轨迹分析法

《自动控制原理》第4章_根轨迹分析法
一般有两个解，从中
因此求分离点和会合点公式： 可以判断是分离点或
N(s)D '(s) N '(s)D(s) 0 会合点，只有满足条
Kg 0
件Kg≥0的是有用解。
例4-1.设系统结构如图， 试绘制其概略根轨迹。
R(s)
k(s 1) c(s)
s(s 2)(s 3)
解：画出 s 平面上的开环零点（-1），开环极点（0， -2，-3）。
逆时针为正。（- ， ）
m
n
pj (2k 1) ( z j pi ) pj pi
j 1
j 1
ji
m
n
zi (2k 1) ( z j zi ) p j zi
j 1
j 1
j i
k 0,1,
k 0, 1,
例3.设系统开环传递函数为： G(s) Kg(s 1.5)(s 2 j)(s 2 j) s(s 2.5)(s 0.5 j1.5)(s 0.5 j1.5)
K
s1
00
0.5 1
1 1 j1
s2
K
K 2.5
2
K 1
1 K 0
1 j1
2 1
2 1 j 3 1 j 3
1 j 1 j
j
2
1
0
K 0.5
1
2
一、根轨迹的一般概念
开环系统（传递函数）的某一个参数从零变化到 无穷大时，闭环系统特征方程根在 s 平面上的轨迹 称为根轨迹。
根轨迹法:图解法求根轨迹。 借助开环传递函数来求闭环系统根轨迹。
nm
独立的渐近线只有（n-m）条 u=0,1…,(n-m-1)
（2）渐近线与实轴的交点
分子除以分母

第四章根轨迹分析法

第四章根轨迹分析法

j=1
i=1 ≠b
例 设系统开环传递函数零、极点的分布如图4-9所
示，试确定根轨迹离开复数共极点- p1 、- p2的出
射角。
解 按公式（4-28），由作图结果得
øb= +180°（2k+1) + - p1+ z1- - p1+ p2-
jw
- p1+ p3- - p1+ p4
S平面
= +180°（2k+1) +45° -90°-135°-26.6°
根轨迹与虚轴相交，意味着闭环特征方程出现 纯虚根。故可在闭环特征方程中令s=jw，然后令 其实部和虚部分别等于0，从中求得交点的坐标 值及其相应的Kg值。 例 设系统的开环传递函数为
Gk（s）=s（s+1K）g（s+2）
试求根轨迹和虚轴的交点，并计算临界根轨迹增 益Kgp。
解 闭环系统的特征方程为 s（s+1）（s+2）+Kg=0
确定根轨迹上某点对应的K*值
例：开环传函 G(s)H(s)= K ，求根轨迹
(s+1)(s+2)
解 1、确定极点、零点
开环 –p1= -1, –p2= -2
无零点
1、相角条件
∠(s+zi)- ∠(s+pj) = 0-[∠(s+1)+ ∠(s+2)] =±180o(2k+1)
试差法 s= -1.5
∠θ1+ ∠θ2=180 o
故 D’(s)=3s2+6s+2
N’(s)=0
解得 s1=-0.423 s2=-1.577
由于s2不在根轨迹上，因而分离点是s1 。

自动控制原理第四章根轨迹法

自动控制原理第四章根轨迹法
仿真与实验研究
根轨迹法可用于仿真和实验研究，通过模拟和实验 验证系统的性能和稳定性，为实际系统的设计和优 化提供依据。
根轨迹法的历史与发展
历史
根轨迹法最早由美国科学家威纳于1940年提出，经过多年的 发展与完善，已经成为自动控制领域中一种重要的分析和设 计方法。
发展
随着计算机技术和数值分析方法的不断发展，根轨迹法的应 用范围和精度得到了进一步拓展和提高。未来，根轨迹法有 望与其他控制理论和方法相结合，形成更加完善和高效的控 制系统分析和设计体系。
根轨迹的性能分析
根轨迹的增益敏感性和鲁棒性
通过分析根轨迹在不同增益下的变化情况，可以评估系统的性能和鲁棒性。
根轨迹与性能指标的关系
通过比较根轨迹与某些性能指标（如超调量、调节时间等），可以评估系统的 性能。
04
根轨迹法与其他控制方法的比较
根轨迹法与PID制根轨迹图，直观地分析系统的稳定性、响应速度和超调量等性
特点
根轨迹法具有直观、简便、易于掌握等优点，特别适合用于分析 开环系统的稳定性和性能。
根轨迹法的应用场景
控制系统设计
根轨迹法可用于控制系统设计，通过调整系统参数 ，优化系统的性能指标，如稳定性、快速性和准确 性等。
故障诊断与排除
根轨迹法可用于故障诊断与排除，通过观察系统根 轨迹的变化，判断系统是否出现故障，以及故障的 类型和程度。
在绘制根轨迹时，需要遵循一定 的规则，如根轨迹与虚轴的交点 、根轨迹的分离点和汇合点等。
03
根轨迹分析方法
根轨迹的形状分析
根轨迹的起点和终点
根轨迹的起点是开环极点的位置，而 终点是闭环极点的位置。通过分析起 点和终点的位置，可以判断根轨迹的 形状。
根轨迹的分支数

第四章根轨迹分析法

第四章根轨迹分析法

闭环系统的阶次为3 ，有3条根轨迹 。
规则三、
证明：（1）连续性 从代数方程的性质可知，当方程中的系数连续变化 时，方程的根也连续，因此特征方程的根轨迹是连 续的。
证明：（2）对称性 因为特征方程的根或为实数，或为共轭复数，所以 根轨迹对称于实轴。
法则三、渐近线：根轨迹有n-m条渐进线。
渐近线与实轴的夹角为： (2k 1)1800 k 0,1,2,..
nm
n
m
pi z j
渐近线与实轴的交点为： i1
j 1
nm
l 它们是针对n-m条趋向无穷远点的根轨迹而设立的
l 如果知道了渐近线，可以马上画出根轨迹的大致形状
法则四、实轴上的根轨迹：在实轴上某线段右侧的实数 开环零、极点个数之和为奇数，则该线段为根轨迹。
对于例题，在实轴上的根轨迹： G(s)H (s) K*(s 5)
若当根轨迹出现在两相邻开环零点间（包括无穷
远处）时，必有一分离点。 分
离 点
K=∞
K=∞
分 离 点
××
K=0
K=0
它们可以利用代数重根法或极值法求出。(介绍后者)
由求极值的公式求出：
1 H (s)G(s) 1 K * N (s) 0 D(s)
K* D(s) N (s)
在实轴根轨迹上，求使K*达到最大（最小）值的s 值:
令虚轴的交点： s j 代入上式，得
( j)3 3( j)2 2 j K ( j 5) 0 Re 5K 3 2 0 Im (2 K ) 3 0 解得： 0，K 0;
本章主要内容
以K*为变量的常规根轨迹的绘制方法 以其它参数为变量的广义根轨迹的绘制方法 根轨迹分析方法的应用
－利用根轨迹分析和设计控制系统

第4章 根轨迹分析法

第4章 根轨迹分析法

i 1
其余n m,
m
(s zi )
i 1 n
(s pj )
m
(1
m
i 1
pj
(1 s)
zi
n
s
) (s
p
j
)
1 Kg
j 1
j 1
j m 1
此时s ，即无穷远处
8/63
五.实轴上的根轨迹
在实轴上，右方的实数开环极点和实数开环零 点的总和为奇数时，此为根轨迹上点。
GK (s)
m
n
闭环系统特征方程 或根轨迹方程
4/63
GK (s) GK (s) e jGK (s) 1
幅值条件: GK (s) 1 相角条件: GK (s) 180o (2k 1) k 0,1, 2,
或:
m
(s zi )
充要条
K i1 gn
1
件
(s pi )
m
n
j 1
s zi s p j 180o (2k 1) k 0,1,2,
当 nm2
n
n
an1 ( pj ) (sj ) s j 为系统的闭环极点
j 1
j 1
随着根轨迹增益的变化，若一些闭环极点向右移动，则另一些
必向左移动
n
(sj )=(-1)n (a0 Kgb0) j 1
22/63
十条法则：
1.连续性 2.对称性 3.分支数 4.起点、终点 5.实轴上的根轨迹 6.渐近线 7.分离点、会合点 8.出射角、入射角 9.虚轴交点 10.闭环极点的和与积
D(s)N(s) N(s)D(s) 0,3s2 6s 2 0
ss21
0.423 1.577

第四章-根轨迹分析法

第四章-根轨迹分析法

i 1
K
K*(sz1) (szm)
(sp1)(sp2) (spn)K 0 K 0 K
6 5
° 3
！绘制注意点
1）实轴、虚轴相同的刻度 5.53
2）“×”、 “〇” 3）加粗线及箭头
4）关键点的标注
j
• K 35, 1.35
1 1
1
0
• K 35, 1.35
29
绘制根轨迹的基本法则
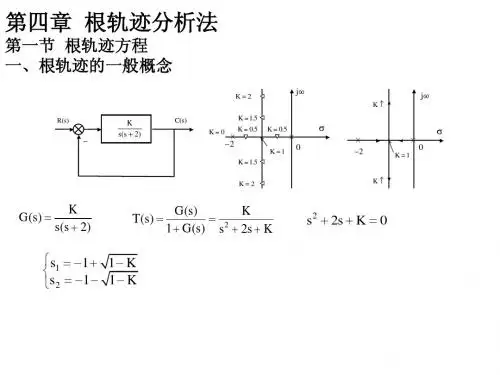
从特征根的表达式中看出每个特征根都随K的变化 而变化。例如，设
K=0 K=0.5 K=1 K=2.5 K=+∞
s1 0, s2 2 s1 1, s2 1 s1 1 j, s2 1 j s1 1 2 j, s2 1 2 j s1 1 j , s2 1 j
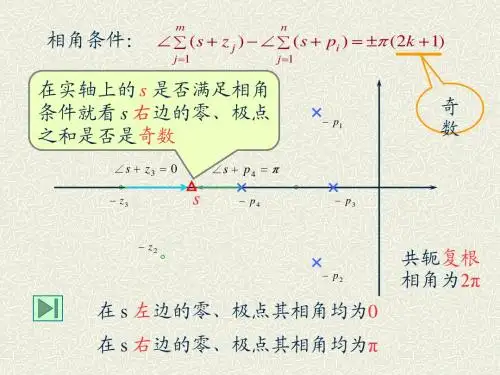
l
h
(szj) (spi)(lh)
j1
i1
•如满足辐角条件必有
(lh)(21)
所以，L-h必为奇数，当然L+h也为奇数。
证毕
36
例3
设一单位负反馈系统的开环传递函数为 G(s)=K(s+1)/[s(0.5s+1)],求 K0 时的闭环根轨迹。
解：将开环传递函数写成零、极点形式 G(s) 2K(s 1) s(s 2)
因此，渐近线交点总在实轴上。
41
例4
已知系统的开环传递函数
G(s)H(s)s(s4 K)g((ss2 12)s2)
试根据6，求出根轨迹的渐近线。
解：
零点 z1, m1 极点 p 10,p2 4,p 3 1j1 ,p4 1j1 ,
n4
42
按照公式得
1800(1 2) 1800(1 2)
nm
➢1.根轨迹的连续性 ➢2.根轨迹分支数 ➢3.根轨迹的对称性 ➢4.根轨迹的起点和终点 ➢5.实轴上的根轨迹 ➢6.根轨迹的渐近线

第四章：根轨迹分析法

第四章：根轨迹分析法

n
m
j
n−m
2k+1 ϕa = π n− m
(k = 0,1,2,⋯, n− m−1)
18
在例4-1中，开环传递函数为
G(s)H(s) =
Kg s(s+ 2)
开环极点数n=2,开环零点数m=0,n-m=2,两条渐近线 在实轴上的交点位置为
−2 σa = = −1 2
π 它们与实轴正方向的交角分别为 (k = 0) 2 3 π 和 (k =1) ，两条渐近线正好与 Kg ≥1 时的根轨迹 2 重合。
在绘 制根轨 迹时 ，可 变参数 不 限定 是 根轨 迹 增 益 Kg ，可为系统的其它参数（如时间常数、反馈系数 等）这时只要把系统的特征方程化为上式，将感兴趣 的系统参数取代根轨迹增益 Kg 的位置都可以绘制根 轨迹。
8
根轨迹方程是一个向量方程，用模和相角的形式 表示
| G(s) H(s) | ej∠G(s)H(s) =1⋅ ej(±180°+k⋅360°) (k = 0,1,2,⋯ )
15
规则三 实轴上的根轨迹
若实轴上某线段右侧的开环零、 若实轴上某线段右侧的开环零、极点的个数之 和为奇数，则该线段是实轴上的根轨迹。 和为奇数，则该线段是实轴上的根轨迹。 例4-3 设系统的开环传递函数为
G(s) H(s) = Kr (s− z1)(s − z2 )(s − z3 )(s − z4 ) (s− p1)(s− p2 )(s− p3 )(s − p4 )(s − p5 )
24
jω
P 1
θ p1
[s]
P 3
0
σ
P 2
θ p2
图4-8(a) 根轨迹的出射角
25
jω

自动控制原理第4章

自动控制原理第4章

z2 ) p2 )
m
sm z j n1
i 1
(s zm )
(s pn )
m
(zj)
j 1
n
( pi )
i 1
自动控制原理
第四章 复域分析法－根轨迹法
如果开环零、极点的数目满足n-m 2，则 闭环特征方程为
snnp isn 1 n( p i)K *m( zj) 0
证明：系统的闭环特征方程
n
m
D(s) (spi)K* (szj)0
i1
j1
根轨迹有分离点，说明闭环特征方程有重
根。因此，
n
m
(s pi ) K* (s zj ) 0
i1
j1
d
ds
n i1
(s
pi )
K*
m j1
(s zj )
0
自动控制原理
第四章 复域分析法－根轨迹法
将上面两式相除，整理得
自动控制原理
第四章 复域分析法－根轨迹法
4.1 根轨迹的基本概念
一、根轨迹的定义
根轨迹：是指系统开环传递函数中某个参数 (如开环增益K)从零变到无穷时，闭环特征 根在s平面上移动所画出的轨迹。
常规根轨迹：当变化的参数为开环增益时 所对应的根轨迹。
广义根轨迹：当变化的参数为开环传递函 数中其它参数时所对应的根轨迹。
自动控制原理
第四章 复域分析法－根轨迹法
证明： 由根轨迹方程，得
m
(s
j 1
n
(s
zj) pi )
1 K*
i1
令K* =0，得
m
j 1 n
(s (s
zj) pi )
1 K*
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
0
Re
4-2 根轨迹绘制的基本法则
一. 绘制根轨迹的基本法则
法则一. 根轨迹的起点和终点
K G ( s) H (s)
*
(s z )
j 1 j i
m
(s p )
i 1
n
* ( s p ) K (s zi ) 0 j j 1 i 1
n
m
s p j ，根轨迹起于开环极点。 当 K * 0 时，
j 1 j i 1 i
m
n
相角条件
K
*
| s z
j 1 i
m
j
| 1
K*
(s p ) (s z )
j 1 j i 1 m i
n
| s p |
i 1
n
模值条件

凡是满足相角条件的点一定是根轨迹上的点（相 角条件是确定根轨迹的充要条件），而其对应的 值由幅值条件求出。
另一方面
K *| s z j |
j 1 m
| s z
1
j 1 n i 1
m
j
|
| s p |
i 1 i
n
| s p |
i
.
1 * K
* K 时，右边 0 当
s zj
或者
s
s zi , 有m条根轨迹终止在开环传递函数的零点。 s ，有（n m）条根轨迹终止在无穷远处。
φ2
z2
θ1
0
sk
θ4
法则四.实轴上根轨迹 考虑幅角条件： ( s z j ) ( s pi ) (2k 1)
j 1 i 1 m n
只有当 sk 点右侧实轴上的开环极点和开环零点的个 数之和为奇数时，才满足相角条件。 结论：实轴上的右边开环零极点个数之和为 奇数时，则此线段为实轴上的根轨迹。

用根轨迹图来分析自动控制系统十分方便。 对于高阶系统，求解特征方程的根非常困难。 如果要研究系统参数的变化对闭环系统特征方程 根的影响，就需要大量反复的计算。 1948年伊万斯（W·R·EVANS）解决了这个问题，提 出了根轨迹法。 根轨迹方法不需要求解闭环系统的特征方程，只 需依据开环传函便可会绘制系统的根轨迹图。
前向通路根 轨迹增益
G ( s ) K1
( s 1)
s (T j s 1)
j 1 i 1 q i
f
* KG
(s z ) (s p
j 1 i 1 h i j
f
)
H ( s) K * H
反馈通路根 轨迹增益
(s z ) (s p
j 1 i 1 h i j




二. 根轨迹方程

通常，系统的开环零、极点已知，因此建 立开环零、极点与闭环极点之间的关系， 有助于闭环系统根轨迹的绘制。
R(s)
－
G(s) H(s)
G (s) (s) 1 G (s) H (s)
C(s)
前向通路传递函数G(s)和反馈通路传递函数H(s) 可分别表示成因式相乘的形式：
j
K
( K 0)
-2
( K 0.5) ( K 0)
-1 0

K
系统的根轨迹
根轨迹变化与系统性能的关系 根轨迹
K
0 1 2 … ∞
s1
0 -1 -1+j … -1+j∞
s2
稳定性
动态性能
系统稳定 过阻尼系统 -2 临界阻尼系统 -1 欠阻尼系统 -1-j … 无阻尼系统 -1-j∞
pj )
sk
nm
n m n m 1 p j zi sk j 1 i 1
(s
j 1 m i 1
n
k
pj ) zi )
.
(s
n
sk n m (n m) a sk n m 1
j
A
a
B -4 -3
180 °
60°
a 0 -2 -1
300°
60°

C
图 根轨迹的渐近线
法则四. 实轴上根轨迹 令 sk 为实轴上的试探点 左侧开环零极点构成 的向量夹角均为零度； 右侧开环零极点构成 的向量夹角均为 ； 一对共轭零点或极点 的向量夹角之和为2 。
p3 j
θ3
i 1 i
n
开环极点
K
*
(s z )
j 1 j i
m
(s p )
i 1
n
1 e j (2 k 1)
K
*
sz
j 1
m
j
e
j ( s z j )

i 1
n
e
j (2 k 1)
s pi e j ( s pi )
(s z ) (s p ) (2k 1)
G(s) H(s) s 2 (s 1)(s 4) K r (s 2)
试画出该系统根轨迹的渐近线。 解：对于该系统有n=4，m=1，n-m=3；三条渐 近线与实轴交点位置为
1 4 2 σa 1 3
它们与实轴正方向的交角分别是
(2k 1) a : , 3 3
第四章 线性系统的根轨迹分析
4-1 根轨迹法的基本概念 4-2 根轨迹绘制的基本法则 4-3 广义根轨迹 4-4 系统性能的分析 (自学)
4-1 根轨迹法的基本概念
一. 根轨迹概念及应用
• • 系统的参数发生变化，其特征方程式的 根的值改变。 当系统参数连续变化时（如从0→∞）， 其特征方程的根在根平面上留下的轨迹， 叫根轨迹。 根轨迹与系统性能密切相关。
n n 1 n n m 1 p j sk p j sk n m 1 j j 1 1 n m 1 p j sk 1 zi sk m m i 1 sk m zi sk m 1 1 zi sk 1 j 1 i 1 i 1
a ) a ) ( sk a ) n m sk n m (n m) a sk n m 1
(s
k
k
n n 1 n n 1 sk p j sk ( sk p j ) p j sk n sk j 1 j 1 j 1 m m m 1 m m 1 m m 1 m m m ( sk zi ) sk zi sk sk zi sk sk z i s k i 1 i 1 i 1 i 1
k
( n m) k p j z i
j 1 i 1
m
a
p z
j 1 j i 1
n
m
i
nm
法则三. 根轨迹的渐近性
(2k 1) a n m n m p j zi i 1 a j 1 nm
例： 已知系统的开环传递函数为
n n
当
sk
m n
1 x 0时， 1 x 1-x
sk
m nm
.
sk m zi sk m 1 i 1
1 zi sk 1 i 1
sk
nm
m 1 m n m 1 nm 1 zi sk sk zi sk i 1 i 1
例:已知单位负反馈系统的开环传递函数为：
K ( s 1) G (s) s (T1s 1)(T2 s 1)
试画出根轨迹。 解：将开环传函进行变换后得到：
K g ( s z1 ) K ( s 1) G (s) s (T1s 1)(T2 s 1) s ( s p1 )( s p2 )
(s
j 1 m i 1
n
m n m nm2 nm n m 1 n m 1 sk zi sk p j sk zi sk i 1 j i 1 1 (sk zi ) k


法则三. 根轨迹的渐近性

当开环极点数n大于开环零点数m时，系统有 n-m条根轨迹终止于S平面的无穷远处，这n-m 条根轨迹变化趋向的直线叫做根轨迹的渐近 线，因此，浙近线也有n-m条，且它们交于实 轴上的一点。

确定渐近线：
1)渐近线与实轴间夹角a 由两个因素决定 2)渐近线与实轴交点 a
l
)
开环系统根轨 迹增益
G ( s) H ( s) K *
( s z ) ( s z ) ( s p ) ( s p
j 1 j j 1 i 1 h i i 1 h i j
f
l
)
开环零点
G ( s) H ( s)
K * (s z j )
j 1
m
(s p )
设 K 的变化范围是〔0, ∞﹚，K 当K 0时, s1 0, s 2 2 ; 当 0 K 0.5 时， s1 与 s 2 为不等的两个负实 根: s1 1 1 2 K , s2 1 1 2 K 当 K 0.5 时， s1 s 2 1,为等实根； 当K 0.5 时， s1,2 1 j 2 K 1为共轭复根; 当 K 时， s1、 s 2 的实部都等于-1，是 常数，虚部趋向无穷远处
夹角 a 计算： 设试探点 sk 在无穷远处的根轨迹上，所以，渐近 线与实轴交角 a 与到各零极点的幅角均相等。