第四章根轨迹法
- 格式:doc
- 大小:2.30 MB
- 文档页数:24










第四章:根轨迹法第四章根轨迹法本章⽬录4.1 根轨迹的⼀般概念4.2 绘制根轨迹的数学依据及其性质4.3 绘制根轨迹的⼀般规则4.4 *绘制根轨迹的MATLAB函数介绍4.5 例题4.6 参数根轨迹和多回路系统的根轨迹4.7 正反馈回路和⾮最⼩相位系统根轨迹——零度根轨迹⼩结本章简介从前章得知闭环极点在根平⾯上的分布,反映着系统的固有性能。
故为了获得较好性能,就希望极点在根平⾯上有较好的分布。
亦即,为了研究系统的动态性能,就可以通过闭环极点在根平⾯上的分布来进⾏。
闭环极点是系统特征⽅程的根sb。
若其特征⽅程中,各系数变化,则⽆疑,其根sb也在变化。
各系数的变化往往相应着系统的许多实际参数的变化⽽形成。
在根迹中,⼀般总是以增益 (当然也可其它参数,如时间常数 )的变化⽽导致各系数的变化,即sb的变化。
如果连续变化,则sb也连续变化。
相应于由0连续变化到∞时, sb在根平⾯上的连续变化⽽形成的轨迹,即闭环系统特征根的根轨迹--若⼲条曲线。
这样,相应于各个值下的闭环极点在根平⾯上的分布就⼀⽬了然了。
这对系统的分析、设计带来了极⼤的⽅便.。
所谓根轨迹法,就是⽤图解的⽅法确定出闭环特征根的⼀种⽅法。
先在复数平⾯上画出系统某⼀参数的全部数值下的特征⽅程的所有根,即根轨迹。
然后⽤图解的⽅法确定出该参数某⼀特定数值时的闭环特征根。
从⽽分析出系统所具有的性能。
或反之,在根迹上先确定出符合系统性能要求的闭环特征根。
从⽽⽤图解的⽅法求出相应的系统应具有的参数值。
相对时域法,很直观,且避免了求解系统⾼阶特征⽅程的困难。
现在计算机科学有了飞速发展,特别是MATLAB语⾔及其相应⼯具箱,有强⼤的数值计算和图形绘制功能。
所以利⽤MATLAB语⾔相关函数绘制系统根迹及求根等均是轻⽽易举的事。
这就给根迹法的应⽤开辟了更好的前景。
本章在介绍传统的根轨迹法及其⽰例的同时,有机结合介绍MATLAB语⾔相关的根轨迹函数及相应⽰例的解题程序。
第 根轨迹法在时域分析法中已知控制系统的闭环特征根决定该控制系统的性能。
那么,是否对于每一个控制系统都必须求出其闭环特征根,才能够了解其性能呢?如果答案是肯定的,那么当特征多项式是三阶及以上时,求解特征根是一项比较复杂的工作。
特别是要分析系统特征式中某一参数(比如K *)变化时对系统性能的影响,这种准确求解每一个特征根的工作将会变得十分困难。
W .R.Evans 提出了一种描述特征方程中某一参数与该方程特征根之间对应关系的图解法,比较方便的解决了上述问题。
这种方法就是本章要介绍的根轨迹法。
第一节 根轨迹的基本概念一、根轨迹的定义系统参数(如开环增益K *)由零增加到∞时,闭环特征根在s 平面移动的轨迹称为该系统的闭环根轨迹。
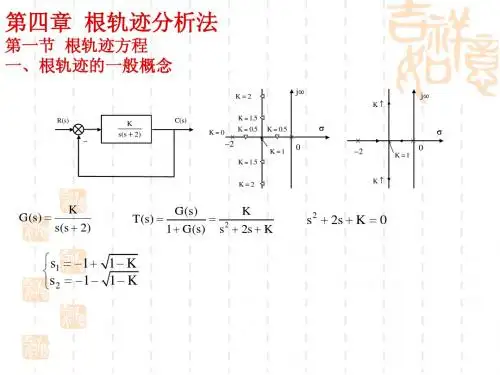
[例4-1] 单位反馈控制系统如图4-1,绘制K *变化时,系统极点的变化情况。
图4-1 反馈控制系统的方块图*2*222)()()(Ks s Ks U s Y s G k ++==特征方程 022)(*2=++=K s s s D 特征根 *2,1211K s -±-= 讨论 当0*=K 时,01=s ,22-=s5.0*=K时,121-==s s1*=K时,112,1j s ±-=∞→*K时,∞±-=j s 12,1绘出特征根的变化轨迹如图4-2σ图4-2 例4-1的根轨迹图显然,当5.00*<<K 时,系统取得二不相等实数根(过阻尼); 5.0*=K 时,系统取得二相等实数根(临界阻尼); 5.0*>K 时,系统取得一对共轭复数根(欠阻尼)。
*K 越大,共轭复数根离对称轴(实轴)越远.指定一个*K 值,就可以在根轨迹上找到对应的二个特征根,指定根轨迹上任意一特征根的位置,就可以求出该特征根对应的*K 值和其余特征根。
下面我们讨论根轨迹的一般情况。
二、根轨迹方程既然根轨迹是闭环特征根随参数变化的轨迹,则描述其变化关系的闭环特征方程就是根轨迹方程。
四根轨迹分析法2-4-1 设系统的开环零、极点分布如题2-4-1图所示,试绘制相应的根轨迹草图。
题2-4-1图【解】:题2-4-1解图2-4-2 设负反馈系统的开环传递函数分别如下:<1) <2)<3)<4)试绘制由变化的闭环根轨迹图。
【解】:<1)系统有三个开环极点。
①,有三条根轨迹,均趋于无穷远。
② 实轴上的根轨迹在区间。
③ 渐近线④ 分离点。
方法一由得不在根轨迹上,舍去。
分离点为。
分离点处K值为方法二特征方程为:重合点处特征方程:令各项系数对应相等求出重合点坐标和重合点处增益取值。
⑤ 根轨迹与虚轴的交点。
系统的特征方程为方法一令,得方法二将特征方程列劳斯表为令行等于0,得。
代入行,得辅助方程⑥ 系统根轨迹如题2-4-2<1)解图所示。
<2)① 根轨迹方程开环零点,开环极点。
② 实轴上的根轨迹区间。
③ 分离会合点方法一均在根轨迹上,为分离点,为会合点。
方法二系统特征方程:重合点处特征方程:联立求解重合点坐标:④ 可以证明复平面上的根轨迹是以为圆心,以为半径的圆<教材已证明)。
根轨迹如题2-4-1<2)解图所示。
b5E2RGbCAP<3)① 开环零点开环极点。
② 实轴上的根轨迹区间为③ 分离点题2-4-2<3)解图为分离点,不在根轨迹上,舍去。
分离点K值④ 出射角⑤ 复平面上的根轨迹是圆心位于、半径为的圆周的一部分,如题2-4-1<3)解图所示。
<4)①四个极点。
②渐近线③实轴上的根轨迹区间为。
④分离点得,均为分离点,。
分离角正好与渐近线重合。
⑤出射角⑥根轨迹与虚轴的交点⑦系统根轨迹如题2-4-1<4)解图所示。
2-4-3 已知单位负反馈系统的开环传递函数为:试绘制由变化的闭环根轨迹图,并求出使系统闭环稳定的值范围。
p1EanqFDPw【解】:系统有两对重极点。
① 渐近线② 实轴上的根轨迹为两点,也为分离点。
分离角均为。
③ 根轨迹与虚轴的交点坐标系统特征方程即令代入特征方程,得令上式实部虚部分别等于0,则有④ 该系统根轨迹如题2-4-3解图所示。
由图可知,当时,闭环系统稳定。
2-4-4 已知单位负反馈系统的开环传递函数为<1)试绘制由变化的闭环根轨迹图;<2)用根轨迹法确定使系统的阶跃响应不出现超调时的值范围;<3)为使系统的根轨迹通过两点,拟加入串联微分校正装置,试确定的取值。
【解】:<1),根据一般根轨迹绘制法则求得①渐近线与实轴的交点:渐近线倾角:。
②实轴上的根轨迹在区间。
③分离点:。
④根轨迹与虚轴的交点坐标:。
⑤ 该系统根轨迹如题2-4-4解图所示。
<2)系统的阶跃响应不出现超调的条件是特征根在左半平面的实轴上。
根轨迹在实轴上的分离点的K值已由<1)求得,所以在时系统不产生超调。
DXDiTa9E3d<3)串联微分校正环节后系统的开环传递函数变为系统特征方程为若是根轨迹上的点,则必满足特征方程。
代入特征方程,得:2-4-5 已知单位负反馈系统的闭环传递函数为<1)试绘制参数由变化的闭环根轨迹图;<2)判断点是否在根轨迹上;<3)由根轨迹求出使闭环系统阻尼比时a的值。
【解】:<1)系统的特征方程为等效开环传递函数为:,a由变化为一般根轨迹。
①开环零点,开环极点。
②实轴上的根轨迹在区间。
③分离点由得解得为分离点,不在根轨迹上,舍去。
④共轭复根的出射角⑤复平面的根轨迹是圆心位于、半径为的圆周的一部分,如题2-4-5解图所示。
<2)把代入相角条件中,若满足则是根轨迹上的点,反之则不是。
点不在根轨迹上。
<3)求等超调线与根轨迹的交点方法一,设等超调线与根轨迹交点坐标实部为,则,有令等式两边s各次项系数分别相等,得方法二由特征方程,按照典型二阶系统近似计算得:另外,把代入特征方程也可求得同样结果。
2-4-6 已知单位负反馈系统的开环传递函数为<1)试绘制参数由变化的闭环根轨迹图;<2)求出临界阻尼比时的闭环传递函数。
【解】:<1)系统特征方程为等效开环传递函数为:a 由变化为一般根轨迹。
①开环极点。
②渐近线与实轴的交点:,渐近线倾角:。
③实轴上的根轨迹在区间。
④分离点由得解得为起点,为分离点。
⑤根轨迹与虚轴的交点令,代入特征方程得⑥ 该系统根轨迹如题2-4-6解图所示。
<2)时,对应实轴上根轨迹的分离点,。
因为,可由开环极点之和等于闭环极点之和求得另一实轴上的极点坐标系统闭环传递函数为2-4-7 已知单位负反馈系统的开环传递函数为:<1)试绘制由变化的闭环根轨迹图;<2)求出使系统产生相重实根和纯虚根时的值。
【解】:<1)根轨迹方程为由变化,为根轨迹。
①开环零点,开环极点。
②实轴上的根轨迹在区间。
③分离点和会合点解得为会合点,为分离点。
④根轨迹与虚轴的交点特征方程为令,代入特征方程得⑤ 该系统根轨迹如题2-4-7解图所示。
<2)实轴上根轨迹的分离点和会合点即为相重实根,其K值分别为纯虚根时的K值即为根轨迹与虚轴交点的K值,由<1)所求得之。
2-4-8系统方框图如题2-4-8图所示,试绘制由变化的闭环根轨迹图。
RTCrpUDGiT【解】:<1)根轨迹方程为由变化为零度根轨迹。
①开环极点。
②实轴上的根轨迹在区间。
③该系统根轨迹如题2-4-8解<1)图所示。
<2)根轨迹方程为由变化为一般根轨迹。
①开环极点。
②渐近线与实轴的交点:,渐近线倾角:。
③实轴上的根轨迹在区间。
题2-4-8解图④分离点<1) <2)题2-4-8解图复平面上的根轨迹与渐近线重合,如题2-4-8解图<2)所示。
5PCzVD7HxA2-4-9单位负反馈系统开环传递函数为,绘制由变化的闭环根轨迹图。
【解】:等效根轨迹方程为当由时为零度根轨迹。
①开环零点,开环极点。
,有一个无穷远的极点。
②实轴上的根轨迹在区间。
③分离点和会合点解得为分离点,为会合点。
④根轨迹与虚轴的交点特征方程为令,代入特征方程得⑤复平面上的根轨迹是圆,如题2-4-9解图所示。
2-4-10 系统方框图如题2-4-10图所示,试求:<1)当闭环极点为时的值;<2)在上面所确定的值下,当由变化的闭环根轨迹图。
【解】:<1)特征方程为闭环极点为时的系统特征方程为两方程联立求解得:<2)系统开环传递函数为等效根轨迹方程为:当由时为一般根轨迹。
①开环零点,开环极点。
②实轴上的根轨迹在区间。
③会合点解得为起点,为会合点,。
④复平面上的根轨迹是圆,如题2-4-10解图所示。
2-4-11 系统闭环特征方程分别如下,试概略绘制由变化的闭环根轨迹图。
<1) <2)【解】:<1)由系统闭环特征方程得等效根轨迹方程为由变化为一般根轨迹。
①开环零点,开环极点。
③分离点和会合点解得<起点),<分离点),<会合点),<舍去)。
④根轨迹与虚轴的交点根据特征方程列劳斯表令行等于零,得,代入行辅助方程,得⑤该系统根轨迹如题2-4-11<1)解图所示。
<2)由系统闭环特征方程得等效根轨迹方程为由变化为一般根轨迹。
①开环零点,开环极点。
②渐近线与实轴的交点渐近线倾角④分离点解得<分离点),<舍去),<舍去)。
⑤根轨迹与虚轴的交点根据特征方程列劳斯表令行等于零,得,代入行辅助方程,得⑥该系统根轨迹如题2-4-11<2)解图所示。
2-4-12 已知单位负反馈系统的开环传递函数为<1)试概略绘制由和变化的闭环根轨迹图;<2)求出其单位阶跃响应为单调衰减、振荡衰减、等幅振荡、增幅振荡、单调增幅时的值。
【解】:<1)特征方程为,等效根轨迹方程为:<a )由变化时为一般根轨迹。
①开环零点,开环极点②实轴上的根轨迹在区间。
③会合点解得<舍去),<会合点)。
④出射角⑤ 复平面的根轨迹是圆心位于、半径为的圆周的一部分,如题2-4-12解图实线部分所示。
<b )由变化为零度根轨迹。
①实轴上的根轨迹在区间。
②会合点计算同上。
会合点为,。
③ 复平面的根轨迹是圆心位于、半径为的圆周的另一部分,如题2-4-12解图虚线部分所示。
<2)由根轨迹看出,根轨迹与虚轴的交点在原点,。
根轨迹在实轴上重合时,。
根轨迹在复平面上时。
结论:系统无等幅和增幅振荡。
在取值时,为衰减振荡;时为单调衰减;时为单调增幅。
2-4-13 系统方框图如题2-3-13图所示,绘制由的闭环根轨迹图,并要求:<1)求无局部反馈时系统单位斜坡响应的稳态误差、阻尼比及调节时间;<2)讨论时局部反馈对系统性能的影响;<3)求临界阻尼时的值。
题2-4-13图【解】: 系统开环传递函数为系统特征方程为)1(1 s s as)(s R )(s E )(s C等效根轨迹方程为由变化为一般根轨迹。
①开环零点,开环极点。
②实轴上的根轨迹在区间。
③会合点解得<舍去),<会合点)。
会合点时的a值④复平面的根轨迹是圆心位于、半径为的圆周的一部分,如题2-4-13解图所示。
(1)稳态误差系统开环传递函数为,Ⅰ型系统,。
阻尼比和调节时间方法一:根据题意,对应根轨迹起点方法二:对应开环传递函数有<2)由根轨迹看出,此时系统特征根为两个不相等的实根,,系统无超调,稳定性变好。
但由于其中一个实根更靠近虚轴,使调节时间增长。
系统仍为Ⅰ型,开环增益减小,斜坡信号输入时稳态误差增大。
jLBHrnAILg<3)系统闭环根轨迹在实轴上出现会合点时为临界阻尼情况,此时。
从特征方程上也可以直接看出。
2-4-14设单位负反馈系统的开环传递函数为确定值,使根轨迹分别具有:0,1,2个分离点,画出这三种情况的根轨迹。
xHAQX74J0X【解】:根轨迹分离点由下式确定,为原点处重极点的分离点,实轴上其他的分离点和汇合点。
<1) 0个分离点只要原点处有两个极点,无论何种情况,至少有一个分离点,所以令,则开环传递函数为当由变化,即零度根轨迹时没有分离点。
其根轨迹如题2-2-14解图<1)所示。
<2) 1个分离点对于一般根轨迹,是一个分离点。
所以当不存在,即,时,根轨迹具有一个分离点。
设渐近线倾角和渐近线与实轴的交点分别为实轴上的根轨迹在区间。
其根轨迹如题2-2-14解图<2)所示。
<3) 2个分离点当或时,有两个分离点。
其中对应零度根轨迹的情况。
设渐近线倾角和渐近线与实轴的交点分别为实轴上的根轨迹在区间。
分离点会合点其根轨迹如题2-2-14解图<3)所示。
LDAYtRyKfE1-0σωj σωj 1-5.0-01-0σωj 45.0-。