当前位置：文档之家 › 第七章 平面立体与曲面立体

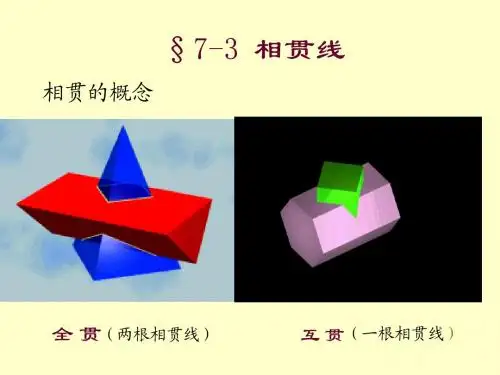
第七章 平面立体与曲面立体

  • 格式：pptx
  • 大小：589.34 KB
  • 文档页数：19

下载文档原格式

  / 19

合集下载

7. 平面立体

7. 平面立体

A′ a
立体表面取点的 步骤﹕ 步骤﹕ AA先由已知点的投性,分析判断该 点所属的表面 表面; 点所属的表面;若该面有 积聚投影, 积聚投影,利用它可直接 补出点的另一投影; 补出点的另一投影;若该 面无积聚投影, 面无积聚投影,则过点在 该面内作一条辅助线, 该面内作一条辅助线,再 于此线上定点, 于此线上定点,并判别可 见性。 见性。
例题
求直线KL与三棱锥的贯穿点 求直线KL与三棱锥的贯穿点 KL
l′
k′ l
k
求贯穿点的方法﹕
P
N M K
L
包含直线作辅助平面,求得该辅助平面与立体的截 交线，而贯穿点是直线与截交线的交点。
作图过程： 作图过程： l′
(n′) m′ 1′ 2′ 3′
PV ① 包含直线作辅 助平面 ② 求辅助平面与 立体的截交线 ③ 求上述截交线 与被包含直线的交点 即贯穿点。
例题 求五棱柱的截交线
4′5′ 3′ 6′ 2′ 1′ 1〞 6″ 2″ 5″ 4″ 3″
分析图形
6 5 1 4 2 3
求截交线上的 转折点 依次连接转折点 完成图形
例题﹕求作正垂面P截割六棱柱的截交线。 PV (5′) 3′ (6′) 2′ 1′
1、棱柱上截交线的求法
⑴ 分析
截平面P与六棱柱的六个 棱面都相交,截交线为一 个六边形;截平面P是正 垂面,其正面投影PV有积 聚性,截交线的正面投影 3〞 积聚在PV上,又因为六棱 柱的六个侧棱面都垂直 2〞于水平面,故截交线的水 平投影积聚在六棱柱各 棱面的水平投影上。所 以只需求截交线的侧面 投影。
求平面立体截交线的方法
• 交点法：求出截平面与立体各棱线的交点，再 按一定的连线原则将交点相连，即得截交线。 • 交线法：求出截平面与立体各棱面的交线，即 得截交线。 • 交点连成截交线的原则是：位于立体的同一表 面的两点才能相连，通常为闭合的平面折线。 位于可见平面的截交线为可见线，画成粗实线， 位于不可见平面的截交线为不可见线，画成细 虚线。

曲面 立体

曲面 立体
例1、求圆柱体截交线
2' 5'（6'）
3'（4'）
7'（8） 1'
4 86
1
2
75
3
2"
解题步骤：
6"
5" 1.进行线面
4"
3" 分析，判断
截交线的形
状和特点.
8"
7" 1"
2.作特殊位
置点的投影.
3.作一般位 置点的投影.
4.画截交线.
5.整理轮廓.
§7-2 平面和曲面立体相交
椭圆的长、短轴随 截平面与圆柱轴线 夹角的变而改变。
nd f
a lc
b e
§7-2 平面和曲面立体相交
[例题5]：求作侧平面Q与圆锥的截交线。
分析： 因截平面Q与圆锥轴线平 行，可知截交线是双曲线(一叶)。它 的正面投影和水平投影均由于Q面的 积聚性而落在QV上和QH上；它的侧 面投影，因Q面与W面平行而具有显 实性。
第二节 平面和曲面立体相交
学习内容：
学
➢ 平面和圆锥的相交形式及截交线画法
习
内
➢ 平面和圆柱的相交形式及截交线画法
容
及 学
➢ 平面和球的相交形式及截交线画法
习 重
学习重点：
点
➢ 平面和曲面立体相交截交线的画法
➢ 辅助平面法
§7-2 平面和曲面立体相交
一、曲面立体截切的基本形式
截交线性质 截交线形状
§7-1 曲面立体的投影
圆柱体的投影分析（回转轴垂直于H面）
侧面投影的左、 右边线分别是圆柱 最前、最后的两条 轮廓素线的投影， 这两条素线把圆柱 分为左、右两半， 它们在V面上的投 影与回转轴的投影 重合。

机械工程图学习题集加详细答案 第7章

机械工程图学习题集加详细答案 第7章

7-5完成被截切圆柱的三面投影。
(2)完成水平和侧面投影
7-5完成被截切圆柱的三面投影。
(3)完成水平和正面投影
7-5完成被截切圆柱的三面投影。
(3)完成水平和正面投影
7-5完成被截切圆柱的三面投影。
(4)完成侧面投影。
7-5完成被截切圆柱的三面投影。
(4)完成水平投影。
7-5完成被截切圆柱的三面投影。
(2)完成水平及侧面投影(注意整理轮廓线)。
7-9完成相贯体(平面立体与曲面立体)的投影。
(2)完成水平及侧面投影(注意整理轮廓线)。
7-9完成相贯体(平面立体与曲面立体)的投影。
(3)完成正面和侧面投影(注意整理轮廓线)。
7-9完成相贯体(平面立体与曲面立体)的投影。
(3)完成正面和侧面投影(注意整理轮廓线)。
7-10完成相贯体(曲面立体与曲面立体)的投影。 (6)
7-10完成相贯体(曲面立体与曲面立体)的投影。 (6)
7-10完成相贯体(曲面立体与曲面立体)的投影。 (7)
7-10完成相贯体(曲面立体与曲面立体)的投影。 (7)
7-10完成相贯体(曲面立体与曲面立体)的投影。 (8)
7-10完成相贯体(曲面立体与曲面立体)的投影。 (8)
7-6完成被截切圆锥的三面投影。
(4)完成水平和侧面投影。
7-6完成被截切圆锥的三面投影。
(5)完成水平和侧面投影。
7-6完成被截切圆锥的三面投影。
(5)完成水平和侧面投影。
7-6完成被截切圆锥的三面投影。
(6)完成水平和侧面投影。
7-6完成被截切圆锥的三面投影。
(6)完成水平和侧面投影。
7-10完成相贯体(曲面立体与曲面立体)的投影。 (1)

相贯线

相贯线

相贯线相贯线概述平面立体与平面立体相贯平面立体与曲面立体相贯曲面立体与曲面立体相贯相贯线概述两立体相交称为相贯，两立体表面的交线称为相贯线。

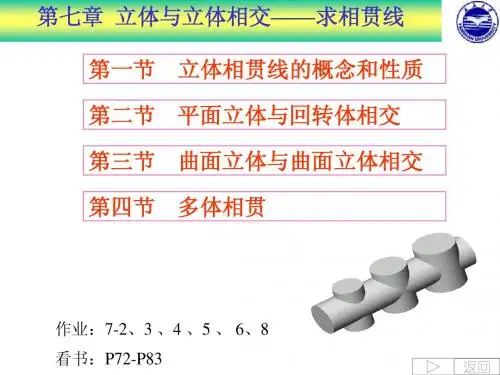
常见的立体相贯分为三种：1）平面立体与平面立体相贯2）平面立体与曲面立体相贯3）曲面立体与曲面立体相贯常见的曲面立体相贯线1、相贯线的性质：1）相贯线是两个立体表面的共有线，相贯线上的点是两个立体表面的共有点；2）相贯线通常是一封闭的空间曲线。

2、相贯线的形状取决于：1）两立体的形状；2）两立体的相对位置。

求相贯线就是求出两立体表面的共有点或共有线。

平面立体与平面立体相贯[例] 试求两三棱柱的相贯线。

[例] 试求四棱柱与三棱锥的相贯线。

平面立体与曲面立体相贯平面立体与曲面立体相贯[例] 试求三棱柱与圆球的相贯线。

曲面立体与曲面立体相贯常用的相贯线作图方法为辅助平面法。

选择辅助平面的原则：辅助平面与两回转面交线的投影都是简单易画的图形——直线或圆。

辅助平面法作图步骤是：1）找特殊点，如转向轮廓线上的点，相贯线的最高、最低、最左、最右、最前、最后点等；2）适当作一些一般点；3）判断可见性将各点依此光滑连成曲线。

判断可见性：相贯线只有同时位于两个立体的可见表面时，相贯线的投影才可见。

[例] 试求圆柱与圆柱的相贯线。

分析：1）对称性：前后、左右对称，故正面投影前后半段重合在一起。

2）积聚性：垂直圆柱的水平投影和水平圆柱的侧面投影都有积聚性，只要作出相贯线的正面投影。

辅助平面为：水平面、正平面、侧平面[例] 试求圆柱与圆柱的相贯线。

两实心圆柱相交圆柱与圆柱孔相交两圆柱孔相交两回转体相对位置的变化引起交线的变化[例] 试求圆柱与圆锥的相贯线。

[例] 试求圆柱与圆锥的相贯线。

曲面立体与曲面立体相贯两回转体的特殊相贯线1) 同轴回转体相贯——相贯线为圆2) 公切于球的两回转体相贯——相贯线为两椭圆曲面立体与曲面立体相贯结束放映。

工程制图B ! 第七章--基本体及其表面上的点和线

工程制图B ! 第七章--基本体及其表面上的点和线

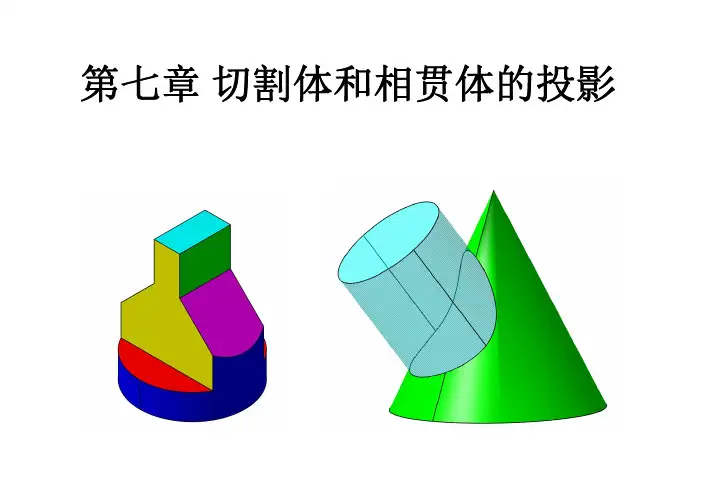
第七章基本体及其表面上的点和线一、平面立体及其表面上的点和线（掌握）二、曲面立体及其表面上的点和线（掌握）平面立体：由若干平面多边形围成的实体。

棱柱棱柱棱锥棱台圆柱圆锥球圆环曲面立体：由曲面和平面或全部由曲面围成的实体。

常见的基本体包括平面立体和曲面立体两大类7-1 平面立体及其表面上的点和线一、平面立体的投影上、下底面平行棱面为平行四边形棱线相互平行棱柱正棱拄——底面为正多边形，且棱线垂直于底面斜棱拄——棱线倾斜于底面棱线交于一点棱面是三角形正棱锥——底面为正多边形，且锥顶与正多边形中心连线垂直于底面棱柱和棱锥均由若干平面多边形围成，故绘制其投影图就是绘制表面的多边形，也即是绘制组成这些多边形的基本几何元素（顶点和边）的投影。

VH 投影分析：棱柱的上顶面、下底面为水平面，前、后棱面为正平面，其余侧棱面则均为铅垂面。

二、棱柱的投影及其表面上的点和线空间状态W1. 画基准线2. 作俯视图（底面实形）3. 作主、左视图三视图aa"a'(b')bb"平面立体表面上的点与平面上取点的方法相同，要判别投影的可见性。

ABB点的位置？AB Cy Ay Aaby cca׳b׳c׳a׳׳b׳׳y c(c׳׳)棱柱体利用积聚性作图VH 投影分析：底面为水平面（等边三角形），水平投影反映实形，其余两面投影积聚成直线。

三个棱锥面（等腰三角形）中，左、右侧棱锥面为一般位置平面，后锥面为侧垂面。

三、棱锥的投影及其表面上的点和线空间状态Wc'a'a"b'b"(c'')abcSS'S"作图步骤：1. 画基准线2. 作俯视图（底面实形）3. 作主、左视图c'a'a"b'b"(c'')abcSS'S"k'k"kK棱锥表面上的点利用辅助线作图（一）——素线法。

第七章立体的投影

第七章立体的投影
1 5 (6) 2 (4) 3 7 (8) 6(8) 4 1(3) 5(7) 2
步骤： 1 分析 空间分析 投影分析 2 作图 • 求特殊点 • 作一般点 • 判别可见性， 并连线 • 整理，检查
6 1 5
4
8 3
2
7
讨论： 1 两正交圆柱相贯线的变化趋势
动 画
交线向大圆 柱一侧弯
Ⅰ
求截交线的实质是求两平面的交线(共有性)。 截交线的每条边都是截平面与立体表面、或截平面与截 平面的交线,顶点是截平面与平面立体的各棱线或边的交点。
3 作图步骤
（1）分析 空间分析：确定截交线的形状。 投影分析：确定截交线投影的形状。 （2）作图 • 作出截平面与各棱线或边的交点;如立体被多个 平面截切,应求出截平面间的交线. • 判别可见性,依次连线; 判别截交线可见性的原则：截交线所在面可见 则截交线可见，否则，不可见。 • 检查,整理.
首先判断点在立体的哪个表面，再具体作图。
k m ( n) k
n
m
n
k
m
圆柱上、下底面上取点同平面取点。 圆柱面上取点应利用圆柱面积聚性的投影作图。
例1 已知圆柱面上的直线AB、曲线BC的正面投影， 求其另外两面投影。
c
c
f d e a(b)
f
a b e d
平面立体——由若干平面围成的立体。 常见的平面立体有棱柱、棱锥和棱台等。
画平面立体的投影，只要画出组成平面立体的平面和 棱线(相邻棱面的交线)的投影，然后判别可见性。 平面立体的棱线和边的投影可见时，画成粗实线；不 可见时，画成虚线；当多种图线发生重叠时，应以粗实线、 虚线、点画线等顺序优先绘制。
二 棱柱
交线为两条平面 曲线（椭圆）

第七章(平-相)

第七章(平-相)

求相贯线的方法
1.线面交点法： 求各侧棱或底边对另一形体表面的交点 2.面面交线法： 求一形体各侧面或底面与另一形体各侧 面的交线
连线规则：
• 把位于甲立体同一侧面又位于乙立体同一 侧面上的两点，依次连接起来。
可见性判断:
•位于甲立体可见面上，又位于乙立体可见面 上的部分，才是可见的。
（三） 直线与平面立体相交
a'
a
c'
6 4 3 5
b' b
a" b"
c"
2 1

c
思考题（2）
如果三棱锥与三棱柱相贯， 相贯线将如何变化？
思考题（3）
如果在三棱锥上钻一个三棱 孔，相贯线又将如何变化？
！ ？
相 贯 线——两立体相交时，它们表面所产生的交线 形状：
一般情况下： 封闭的空间折线
特殊情况下：
封闭的平面图形
折线的顶点是两平面体上参与相交的棱线与平面体的交点
一、 两平面体相贯
（二） 求相贯线的方法：
（1） 求各棱线与立体表面的交点； （2） 依次连接各交点，同表面交 点相连； （3） 判定可见性。
3'
(n') 例题1：求直线与三棱锥的贯穿点
s’
m'
s"
(n')
3'
(n")
Pv a'
1'
2'
m"
b' 1 s
m
a
n
c'
a"
c"
b"
2
3
c
b
例题2：求直线与四棱柱的贯穿点

平面立体曲面立体的投影

平面立体曲面立体的投影
2．曲面立体投影及面上点的投影
归纳法
多媒体演示
学生倾听
10分钟
作业（思考与练习）
将长方体切割一个三棱柱后其投影画法（用橡皮泥完成）
P10
教师说明作业要求
讲授法
学生倾听
5分钟
后记
高职教改课程教学设计案例集——清华大学出版社
中华人民共和国建设部主编《建筑制图标准》GB/T50104-2001），北京，中国计划出版社
二、教学设计
步骤
教学内容
教学方法
教学手段
学生活动
时间分配
复习旧课
特殊位置直线的投影规律
一般位置直线的投影规律
讲授法
多媒体
学生倾听
10分钟
告知
（教学内容、目的）
1告知本课程的能力目标：最终目标：能熟练绘出基本几何平面立体、曲面立体图形的三面投影
《道路工程制图》课程单元教学设计
《平面立体与曲面立体的投影》
一、教案头NO 5
本次课标题：平面投影及点、线、面综合训练
授课班级
111641
上课时间：11月2日1-4
4课时
上课地点
213、214
教
学
目
标
能力（技能）目标
知识目标
最终目标：能熟练绘出基本几何平面立体、曲面立体图形的三面投影
促成目标：
1．熟练绘出点、直线、平面的三面投影
促成目标：
1．熟练绘出点、直线、平面的三面投影
2．熟练运用平面的投影特征及平面上求点的方法对位置的投影
讲授
教师讲授
学生倾听
10分钟
2告知本课程的知识目标：1．掌握长方体、三棱柱平面立体投影特征
2．掌握平面立体表面上的点、直线的投影画法

第七章 求相贯线

第七章 求相贯线

三 相贯线的形状及投影 相贯线为封闭的空间折线。 相贯线为封闭的空间折线。相贯线在非积聚 封闭的空间折线 性投影上总是向被穿的回转体里面弯折 向被穿的回转体里面弯折， 性投影上总是向被穿的回转体里面弯折，而且在 两体相交区域内不应有回转体轮廓线的投影 相交区域内不应有回转体轮廓线的投影。 两体相交区域内不应有回转体轮廓线的投影。
返回
求圆柱与圆锥的相贯线（辅助平面法） 例3 求圆柱与圆锥的相贯线（辅助平面法）
y PV QV RV
返回
例 4
辅助平面的选择原则： 辅助平面的选择原则： 选择原则 使辅助平面与 辅助平面与 两回转体表面 表面截交 两回转体表面截交 线的投影简单易画 简单易画， 线的投影简单易画， 例如直线 直线或 例如直线或圆。
圆柱才可用
返回
例2 两圆柱筒相贯 •内外分别求 内外分别求 •先求特殊点 先求特殊点 •本例以圆弧近似 本例以圆弧近似 代替相贯线
返回
2、利用辅助平面法 、利用辅助平面法
选辅助平面的原则： 选辅助平面的原则： 要使辅助平面与两立体表面交线的投影为直线 直线或 要使辅助平面与两立体表面交线的投影为直线或圆, 常用的辅助平面为投影面的平行面或垂直面。 平行面或垂直面 常用的辅助平面为投影面的平行面或垂直面。
立体与立体相交——求相贯线 第七章 立体与立体相交 求相贯线 第一节 立体相贯线的概念和性质 平面立体与回转体相交 第二节 平面立体与回转体相交 第三节 曲面立体与曲面立体相交 多体相贯 第四节 多体相贯
作业：7-2、3 、4 、5 、 6、8 看书：P72-P83
返回
第一节 立体相贯线的概念和性质
返回
4、依次连接各点 5、判断可见性 、 、
平面立体与回转体相交 第二节 平面立体与回转体相交

第七章~《画法几何》

第七章~《画法几何》

由锥顶S过M做辅助线SH，因点M在SH上，则点M的投影必在直线SH的同面投影上。因此，下面为求作棱锥表面上点的另一种
作图方法。
作图步骤（方法二）：
① 如图7-8所示，在俯视图中连接sm交直线ab于点h。
② 点H在底面ABC的线段AB上，ABC为水平面，根据
“长对正”得到h′，连接s′h′。
③ m′在直线s′h′上，根据“长对正”得到m′。 ④ 根据点的投影规律，由点m′和点m求出点M的侧面投 影m″，如图7-8（c）所示。
（a）
（b）
图7-4 作棱柱表面上点的投影
8
画法几何
7.1.2 棱锥及其表面上点的投影
1．棱锥的投影
棱锥由一个多边形底面和若干个侧棱面组成，相邻两侧面的交线称为棱 线，各侧棱线均过锥顶，常见的棱锥有三棱锥、四棱锥、五棱锥等。当底面为 正多边形，锥顶在底面多边形高线上时，形成的棱锥称为正棱锥。
棱锥的作图方法：一般先画底面的三面投影（先画底面多边形的投影）， 再画锥顶的三面投影，最后连接锥顶与底面各顶点，即为棱锥的三视图投影。 按图7-5位置放置棱锥，其底面平行于水平投影面（H面），水平投影反映实 形，其他两个投影积聚成直线，再画锥顶的三面投影，连接各侧棱线的同面投 影，即为棱锥的投影。
【例7-2】 已知三棱锥表面上点M和点N的正面投影，试求作其水平投影和侧面投影。
作图步骤（方法一）： ① 如图7-7（a）所示，由于点M的正面投影不可见，因此该点在后棱 面SAC上。由于此棱面是侧垂面，其侧面投影具有积聚性，因此点M的侧面 投影m''一定积聚在直线s''a''上，根据点的投影规律求出点m''。最后由点m'和 点m''求出M点的水平投影m。 ② 由于点N的正面投影可见，因此该点在右侧棱面SBC上。首先通过点 n'作辅助线n'1'平行于b'c'并交s'c'于点1' ；然后求出Ⅰ点的水平投影1；接着 过点1作平行于bc的直线；最后根据点的投影规律求出点N的水平投影n。根 据点的投影规律，由点n'和点n求出点N的侧面投影n''，如图7-7（b）所示。

第七章 平面立体与曲面立体

第七章 平面立体与曲面立体
《土木工程制图与识图》
建筑工程学院 主讲人：许胜才、邱秀丽、韩晶晶
第7章 平面立体与曲面立体
第7章 平面立体与曲面立体
1 2
基本概念
平面立体 曲面立体
3
基本概念
平面立体 表面全是平面的立体。 棱面 平面立体的每个表面 是平面多边形
基本平面立体 棱柱、棱锥
棱线 棱面的交线
平面立体的投影，实 质上是各棱面、各棱 线及各顶点的投影。
画五条棱线 V、W投影
b’
d’ c’ d s c
e” (d”)
a” (c”)
b”
e
a
b
棱锥体投影图作图基本步骤均为底面投影、锥顶的VW投影、棱线的VW投影。
平面立体——棱台体
将棱锥体用平行于底面的平面切割后去上部，余下的部分称为棱台体。
棱台的两个底面为相互平行的相似的平面图形。
V
长
高
W
宽
四棱台的投影图
作平面立体表面上的点和线的投影时， 应遵循点、线 、面、体之间的从属性关系。
顶点 棱线的交点
平面立体——棱柱体
直棱柱
棱线垂直于 底面棱柱
底面
棱柱上平行的上下两个 表面
斜棱柱
棱线与底面 斜交的棱柱
棱柱
棱面
除底面以外的称为棱柱的 侧面或棱面
正棱柱
底面是正多边形的 直棱柱 上下底面平行 棱线互相平行的平面立体
e”(d”)
s”
s” a’ e’
a”(c”)
பைடு நூலகம்b’
d’ c’ d s c
e” (d”)
a” (c”)
b”
C s
e
d B c
b
b”
a H

7 平面立体及回转体的投影

7 平面立体及回转体的投影
基本体和切割体
1. 平面立体的投影 2. 曲面立体（回转体）的投影
平面立体：表面都是平面多边形的立体
曲面立体：既有平面、又有曲面的立体
常见的基本几何体 平面基本体 曲面基本体
平面立体的投影
平面立体的投影实质是关于其表面上点、线、 面投影的集合，且以棱边的投影为主要特征，对 于可见的轮廓线，其投影以粗实线表示，不可见 的轮廓线，则以虚线表示。在投影图中，当多种 图线发生重叠时，应以粗实线、虚线、点画线等 顺序优先绘制。
a”
(b)
a
三、圆球表面上取线
end
例1 已知半圆柱体的俯视图，其高度为50 mm， 补画主 、左视图，并完成半圆柱体上点 A 和B 的投影。
例2 已知四分之一圆台的左视图，其长度为50 mm， 补画主 、俯视图，并完成四分之一圆台上线CD 的投影。
例3 已知二分之一圆球体的主视图及其半径大小 ，补画俯、左视图，并完成球体上线EF 的投影。
例4 已知鼓形体的三视图，补画其上线GH 的 另外两个投影。
s’
Z
s”
a’
X
c’ s
b’
b
O a”(b”)
c”
YW V
Z s' S a' b' A a s
a
s"
W Ca" c" Bc b"
YH 正三棱锥的三面投影图
c
X
b
Y
3、三棱锥表面上取点M
方法一： Z s’ s” S
素线
m’ a’
X
2’ c’
b’ b
m”
a”(b”)
c”
YW
M
a
s
2 m c

《工程制图与识图》第七章 相贯线

《工程制图与识图》第七章 相贯线

((cd))作清(图a理)过已图程知面和条后结件的果投影图
(b)解题分析
图2.187 补全具有三棱柱孔的三棱锥的投影
7.2 平面立体和曲面立体相交
平面立体和曲面立体相交，其相贯线是由若 干段平面曲线或由若干段平面曲线和直线所组成。 每一段平面曲线或直线的转折点，就是平面立体 的棱线对曲面体表面的贯穿点。因此，求平面立 体与曲面立体的相贯线，可归结为求平面、直线 与曲面立体表面的交线和交点。
例7-3：求三棱柱与半球的相贯线。
a"
a
7.3 两曲面立体相交
●Hale Waihona Puke ●●●●
例7-4：圆柱与圆柱相贯，求其相贯线。
●
●
●
●
求相贯线的投影：
空间及投影分析： 小圆利柱用轴积线聚垂性直，于采H面，水平投 影积用聚表为面圆取，点根法据。相贯线的共有
性，☆相找贯特线殊的点水平投影即为该圆。 大圆☆柱补轴充线中垂间直点于W面，侧面投 影积☆聚光为滑圆连，接相贯线的侧面投影
在该圆上。
相贯后的三视图：
7.3 两曲面立体相交
例7-5 求圆柱与圆锥的相贯线。
素线法
7.3 两曲面立体相交
相贯线为平面曲线 球面法求解
球面法求解的条件： 1、两立体为回转体。 2、两立体轴线平行 一投影面，且相交。
3、平行一投影面的 两立体交线可用球面 法求解。
4、两立体若存在一 公共内切球，则此相 贯线为平面曲线。
(b)解题分析
图2.186 作三棱柱与三棱锥的相贯线，并补全投影
如图所示，三棱锥被前后穿通了一个正三棱柱形状的贯通孔， 求作孔口线的水平投影，补全这个具有三棱柱贯通孔的三棱 锥的水平投影，并作出它的侧面投影。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
H
四棱台的立体图
棱台体投影图作图方式与棱锥体类似，不同点是棱椎体顶点变成棱台体顶面 10
宽
平面立体的投影性质
三面投影的度量关系
V面投影反映了 形体的正面形状 和长度及高度
Z
W 面投影反映了形 体的左侧面形状和 高度及宽度
高
高
长
宽
X
长
H 面 投 影反映 了 形体水平面的形 状和长度及宽度
O
YW
宽
YH
平面立体的投影性质
三面正投影的投影关系
高
V面投影和H面投影 “长相等”
Z
高
V面投影和W面投 影“高相等”
长
宽
X
长
O
YW
H面投影和W面投 影“宽相等”
宽
YH
长对正 高平齐 宽相等
平面立体表面上取点和直线
【例】已知棱柱上点K及直线MN的V投影，求H、W投影
Z
k’ m’ K N X M O YH k”
平面立体——棱椎体 棱锥体的基本概念
棱锥
底面是多边形，各个棱面 都是有一个公共点的三角 形的平面体。
S
C B
D
E
A
正棱锥
底面是正多边形，顶点与正多边 形中心的连线垂直于底面的棱锥 称为正棱锥。
底面为几边形即为几棱锥，如底面三角形——三棱锥；底面四边形——四棱锥等
平面立体——棱椎体
s’ V V s’ W S a’ e’ b’ d’ c’ E e A D
棱线
相邻的两棱面的交线
平面立体——棱柱体
e' c"(f") d(f') a'
V
b"(e")
W
a' b"(d") b'(c') c a
e' d’(f') f c"(f")
a"(e") b"(d")
F C A B
f c a b
E D
e d
b'(c')
e
b
d
立体图
投影图
三棱柱的投影特性:长对正；宽相等、高平齐
曲面立体——回转面与回转体
过点作锥面上垂直于轴线的纬圆，求出纬圆的各个投影。 由于点在纬圆上，则点的投影一定在纬圆的同面投影上。
Z
M
X m
m'
m"
YW
m YH
17
本章总结
1
平面立体与曲面立体的基本概念；
2
3
平面立体与曲面立体的分类；
平面立体与曲面立体的投影作图 的基本步骤。
e”(d”)
s”
s” a’ e’
a”(c”)
b’
d’ c’ d s c
e” (d”)
a” (c”)
b”
C s
e
d B c
b
b”
a H
a
b
五棱锥的立体图
五棱锥的投影图
五棱锥的立体图与投影图的对比。直线为可见线，虚线为不可见线。
平面立体——棱椎体
画底面投影
s’
s”
作图步骤
画锥顶的 V W投影
a’ e’
作平面立体表面上的点和线的投影时， 应遵循点、线 、面、体之间的从属性关系。
顶点 棱线的交点
平面立体——棱柱体
直棱柱
棱线垂直于 底面棱柱
底面
棱柱上平行的上下两个 表面
斜棱柱
棱线与底面 斜交的棱柱
棱柱
棱面
除底面以外的称为棱柱的 侧面或棱面
正棱柱
底面是正多边形的 直棱柱 上下底面平行 棱线互相平行的平面立体
《土木工程制图与识图》
建筑工程学院 主讲人：许胜才、邱秀丽、韩晶晶
第7章 平面立体与曲面立体
第7章 平面立体与曲面立体
1 2
基本概念
平面立体 曲面立体
3
基本概念
平面立体 表面全是平面的立体。 棱面 平面立体的每个表面 是平面多边形
基本平面立体 棱柱、棱锥
棱线 棱面的交线
平面立体的投影，实 质上是各棱面、各棱 线及各顶点的投影。
n’
（n”）
（ m”）
n
k m
YW
曲面立体——回转面与回转体
（ 1 ）圆锥面的形成
圆锥面是由直母线绕与它相交于一点 的轴线旋转一周而形成的曲面。 素线
轴线
母线
由圆锥面和底面组成的回转体就是圆 锥体，简称圆锥。
当圆周所在平面与轴线垂直时，称 为正圆锥。
底圆
曲面立体——回转面与回转体
（2）圆锥的投影
画五条棱线 V、W投影
b’
d’ c’ d s c
e” (d”)
a” (c”)
b”
e
a
b
棱锥体投影图作图基本步骤均为底面投影、锥顶的VW投影、棱线的VW投影。
平面立体——棱台体
将棱锥体用平行于底面的平面切割后去上部，余下的部分称为棱台体。
棱台的两个底面为相互平行的相似的平面图形。
V
பைடு நூலகம்
长
高
W
宽
四棱台的投影图
V面投影是等腰三角形
Z
W面投影是等腰三角形
X
O
YW
H面投影是一个圆周
YH
曲面立体——回转面与回转体
1)求圆锥面上点的方法—素线法
Z
m'
M
X N O m n n m YH n'
m"
n" YW
素线法是过已知点作圆锥的素线，先求素线的投影，然后用线上定点的方法求点的投影。
2)求圆锥面上点的方法—纬圆法