平面立体与曲面体相贯
- 格式:ppt
- 大小:76.00 KB
- 文档页数:3




题目:基本形体可分为两大类,分别为()选项A:平面立体和曲面立体选项B:立方体和长方体选项C:正方体和球体选项D:棱柱体和棱锥体答案:平面立体和曲面立体题目:正三棱柱放置位置为上下三角形底面为水平面,则其W面投影形状为()选项A:直线选项B:矩形选项C:三角形选项D:不能确定答案:矩形, 直线题目:正三棱柱放置位置为上下三角形底面为水平面,则其V面投影形状轮廓为()选项A:不能确定选项B:矩形选项C:三角形选项D:直线答案:矩形, 直线题目:下列关于棱台说法错误的一项是()选项A:棱台的两个底面为相互平行的相似的平面图形选项B:棱台是棱锥顶部被平行于底面的平面切割后形成的选项C:所有的棱线延长后仍应汇交于一公共顶点,即锥顶选项D:正四棱台上下底面为水平面,左右侧面为正垂面,则前后侧面为铅垂面答案:正四棱台上下底面为水平面,左右侧面为正垂面,则前后侧面为铅垂面题目:下列各形体均属于曲面立体的是()选项A:三棱锥、三棱台、立方体选项B:三棱台、四棱台、无棱台选项C:球体、圆锥体、圆柱体选项D:三棱锥、圆锥、四棱锥答案:球体、圆锥体、圆柱体题目:某圆柱其轴线垂直于水平面,其上下底面为水平圆,则圆柱面上各素线为()选项A:铅垂线选项B:正平线选项C:侧垂线选项D:水平线答案:铅垂线题目:下列关于圆锥及投影作图方法说法有误的一项是()选项A:绘制圆锥投影时,通常最后画出圆锥在各投影位置上的对称中心线选项B:圆锥是由底面和圆锥面组成的选项C:圆锥的轴线垂直于水平面时,圆锥底面为水平圆选项D:圆锥底面为水平圆时,其正面投影和侧面投影积聚为正平线答案:圆锥底面为水平圆时,其正面投影和侧面投影积聚为正平线题目:下列关于圆球及投影作图方法说法有误的一项是()选项A:画球的投影应先定球心,画出中心线,作圆选项B:球面的三个投影为三个大小不等的圆选项C:球面是以圆作为母线,以该圆直径为轴线旋转而成选项D:圆球的表面就是球面答案:球面的三个投影为三个大小不等的圆题目:下列关于截交线说法有误的一项是()选项A:截交线既在截平面上,又在立体表面上选项B:截交线是截平面与立体表面的共有线选项C:截平面与立体表面的交线称为截交线选项D:曲面体截交线的形状一定是由直线段围成的平面多边形答案:曲面体截交线的形状一定是由直线段围成的平面多边形题目:下列关于圆柱截交线说法有误的一项是()选项A:根据平面与圆柱轴线的相对位置的不同,其截交线形状不同选项B:当截平面垂直于圆柱轴线时,它与圆柱面的截交线为一纬圆选项C:当截平面倾斜于圆柱轴线时,它与圆柱面的截交线为一椭圆选项D:当截平面平行于圆柱轴线时,它与圆柱面的截交线为一圆形答案:当截平面平行于圆柱轴线时,它与圆柱面的截交线为一圆形题目:平面切割圆锥时,根据平面与圆柱轴线的相对位置的不同,其截交线的形状不可能为()选项A:四边形选项B:圆形选项C:椭圆形选项D:三角形答案:四边形题目:平面立体又分为()选项A:正方体和球体选项B:平面立体和曲面立体选项C:立方体和长方体选项D:棱柱体和棱锥体答案:棱柱体和棱锥体题目:平面切割圆球时,其截交线的形状为()选项A:三角形选项B:圆形选项C:椭圆形选项D:四边形答案:圆形题目:平面切割圆球时,其截交线的投影不可能是()选项A:四边形选项B:圆形选项C:三角形选项D:椭圆形答案:四边形题目:下列关于圆球截交线说法有误的一项是()选项A:当截平面与投影面倾斜时,截交线圆在投影面上的投影为椭圆选项B:当截平面与投影面平行时,截交线圆的投影反映实形选项C:当截平面与投影面垂直时,截交线圆在投影面上的投影为抛物线选项D:当截平面与投影面平行时,截交线圆的另二投影重影成长度等于该圆直径的直线段答案:当截平面与投影面垂直时,截交线圆在投影面上的投影为抛物线题目:相贯体表面的交线称为()选项A:相贯线选项B:素线选项C:双曲线选项D:截交线答案:相贯线题目:下列关于形体相贯线说法有误的一项是()选项A:两曲面立体相交,其相贯线通常为平面多边形选项B:相贯线是两个相交立体表面的共有线选项C:相贯线上的点即为两个形体表面的共有点选项D:两平面立体相交,其相贯线在一般情况下是封闭的空间折线答案:两曲面立体相交,其相贯线通常为平面多边形题目:下列关于平面立体和曲面立体的相贯说法有误的一项是()选项A:平面体与曲面体相交时,相贯线是由若干段平面曲线或平面曲线和直线所组成选项B:绘制相贯线时,应先求每段曲线和直线,再求出曲线和直线的转折点选项C:相贯线上的点即为两个形体表面的共有点选项D:相贯线是两个相交立体表面的共有线答案:绘制相贯线时,应先求每段曲线和直线,再求出曲线和直线的转折点题目:两曲面体的相贯线的形状绝大多数为()选项A:空间曲线选项B:平面曲线选项C:空间直线选项D:平面直线题目:侧棱垂直于底面的棱柱为()选项A:不能确定选项B:直棱柱选项C:斜棱柱选项D:正棱柱答案:直棱柱题目:侧棱倾斜于底面的棱柱为()选项A:直棱柱选项B:斜棱柱选项C:正棱柱选项D:不能确定答案:斜棱柱题目:当直棱柱的底面为正多边形时,称为()选项A:正棱柱选项B:直棱柱选项C:不能确定选项D:斜棱柱答案:正棱柱题目:当长方体放置位置为上下底面为水平面,前后两个侧面为正平面,则左右两个侧面为()选项A:水平面选项B:铅垂面选项C:侧平面选项D:侧垂面答案:侧平面题目:当长方体放置位置为前后两个侧面为正平面,则左右两个侧面为侧平面,则上下底面为()选项A:侧垂面选项B:铅垂面选项C:水平面选项D:侧平面答案:水平面题目:正六棱柱放置位置为上下底面为水平面,前后两个侧面为正平面,则左右四个侧面为()选项A:侧垂面选项B:铅垂面选项C:侧平面答案:铅垂面题目:当长方体放置位置为上下底面为水平面,左右两个侧面为侧平面,则前后两个侧面为()选项A:侧垂面选项B:水平面选项C:铅垂面选项D:侧平面答案:侧平面题目:将形体的某一局部结构形状向基本投影面作正投影,所得到的投影图称为()选项A:背立面图选项B:局部视图选项C:斜视图选项D:基本视图答案:基本视图题目:为了表达形体倾斜于基本投影面部分的真实形状,可以设置一个与该部分表面平行的辅助投影面,然后将该部分向辅助投影面作正投影,所得到的视图称为()选项A:背立面图选项B:基本视图选项C:局部视图选项D:斜视图答案:斜视图题目:下列关于剖面图相关说法有误的一项是()选项A:同一物体若需要几个剖面图表示时,可进行几次剖切,且互不影响选项B:在每一次剖切前,都应按整个物体进行考虑选项C:对剖切面没有切到、但沿投射方向可以看见部分的轮廓线不得用中粗实线画出选项D:剖切是一个假想的作图过程,目的是为了清楚地表达物体内部形状答案:同一物体若需要几个剖面图表示时,可进行几次剖切,且互不影响题目:假想用剖切平面将物体切断,仅画出该剖切面与物体接触部分的图形,并在该图形内画上相应的材料图例,这样的图形称为()选项A:基本视图选项B:背立面图选项C:局部视图选项D:斜视图答案:题目:下列关于组合体相关说法有误的一项是()选项A:组合体的组合方式可以是叠加、相贯、相切、切割等多种形式选项B:组合体是由若干个基本几何体组合而成选项C:绘制组合体的投影图最后一步是进行形体分析选项D:表达组合体一般情况下是画三投影图,从投影的角度讲三投影图已能唯一的确定形体答案:绘制组合体的投影图最后一步是进行形体分析题目:为能正确、迅速、清晰地画出组合体的三面投影图,首先应()选项A:检查所画的投影图是否正确选项B:逐个画出各组成部分的投影选项C:进行形体分析选项D:进行投影分析,确定投影方案答案:进行形体分析题目:读图的基本方法可概括为两类,分别为()选项A:形体分析和线面分析选项B:归纳分析和验算分析选项C:形体分析和计算归结选项D:计算归结和线面分析答案:形体分析和线面分析题目:下列关于轴侧投影图性质说法有误的一项是()选项A:形体上平行于某坐标轴的直线,其轴测投影垂直于相应的轴测轴选项B:轴测投影是在单一投影面上获得的平行投影选项C:平行二线段长度之比,等于其轴测投影长度之比选项D:空间平行的线段,其轴测投影仍相互平行答案:形体上平行于某坐标轴的直线,其轴测投影垂直于相应的轴测轴题目:下面关于轴侧图相关说法有误的一项是()选项A:正轴测图投影方向垂直于投影面,比较接近人的视觉选项B:轴测图轴间角是特殊角,三个轴间角均为120°选项C:常用的轴测图有正等轴测图、正面斜二轴测图和水平斜轴测图选项D:正轴测图的轴向伸缩系数为2答案:正轴测图投影方向垂直于投影面,比较接近人的视觉。



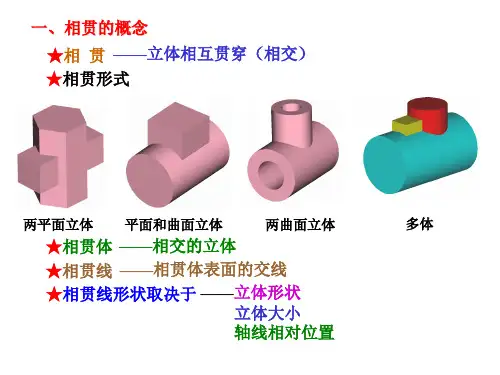
9.1 两平面立体相贯9.2 同坡屋面9.3 平面立体与曲面立体相贯9.4 两曲面立体相贯9.5 常见曲面立体相贯线的讨论两立体相交,也称两立体相贯,它们表面的交线称为相贯线。
工程形体一般是多种几何形体的组合,当这些基本几何体表面相交时,会产生相贯线。
相贯线是几何体表面的分界线。
在绘制工程形体的视图时,需要画出相贯线的投影。
坝体与闸墩之间、进水口处、两廊道相交处均有相贯线。
立体与立体相贯可分为三种情况:(1)两平面立体相交。
(2)平面立体与曲面立体相交。
(3)两曲面立体相交。
由于立体的形状、大小及相互位置的不同,相贯线的形状也各不相同,可能是直线段或平面曲线段的组合,也可能是空间曲线。
但是,所有相贯线都有下列基本性质:1. 相贯线是相交两立体表面的共有线,它的投影必在两立体投影重叠部分的范围以内;2. 由于立体有一定的范围,所以相贯线一般是封闭的;3. 相贯线是相交立体表面间的分界线,每个参加相交的立体的轮廓线都不能穿过相贯线而进入另一立体内部。
当一立体全部棱线或素线与另一立体表面相交时称为全贯,全贯时一般有两条相贯线;当两立体都只有部分棱线或素线与另一立体表面相交时称为互贯,互贯时则只有一条相贯线。
求相贯线实质上是求两立体表面一系列共有点,然后依次光滑连接,并判别可见性。
一般地说这些共有点是一个立体的素线与另一立体表面的交点,也称为贯穿点。
求相贯线的步骤一般如下:1.分析两立体的相对位置及其相对于投影面的位置;2.分析相贯线的性质——空间形状及投影情况,选择解题方法;3.求相贯线上的控制点及中间点。
控制点包括:轮廓线(棱线)上的点,极限位置点——最高最低点、最左最右点、最前最后点,相贯线端点,曲线特征点(如椭圆的长短轴端点、曲线的拐点等);4.根据相贯线的性质依次连接所求各点;5.区别相贯线各段的可见性,并补全立体的投影。
判别相贯线可见性的原则只有位于两形体都可见的表面上的交线,是可见的。
只要有一个表面不可见,则交线就不可见。