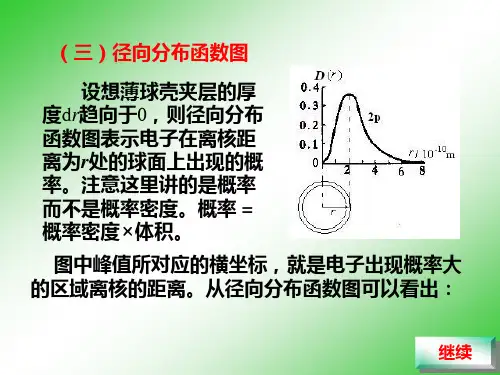
氢原子的径向概率密度
- 格式:ppt
- 大小:1.09 MB
- 文档页数:9





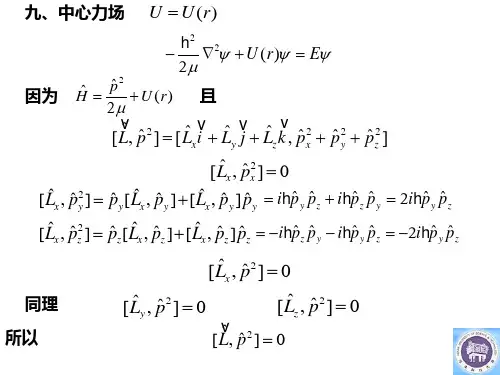

量子力学期末考试题解答题[标签:标题]篇一:量子力学期末考试题解答题1. 你认为Bohr的量子理论有哪些成功之处?有哪些不成功的地方?试举一例说明。
(简述波尔的原子理论,为什么说玻尔的原子理论是半经典半量子的?)答:Bohr理论中核心的思想有两条:一是原子具有能量不连续的定态的概念;二是两个定态之间的量子跃迁的概念及频率条件。
首先,Bohr的量子理论虽然能成功的说明氢原子光谱的规律性,但对于复杂原子光谱,甚至对于氦原子光谱,Bohr理论就遇到了极大的困难(这里有些困难是人们尚未认识到电子的自旋问题),对于光谱学中的谱线的相对强度这个问题,在Bohr理论中虽然借助于对应原理得到了一些有价值的结果,但不能提供系统解决它的办法;其次,Bohr理论只能处理简单的周期运动,而不能处理非束缚态问题,例如:散射;再其次,从理论体系上来看,Bohr理论提出的原子能量不连续概念和角动量量子化条件等,与经典力学不相容的,多少带有人为的性质,并未从根本上解决不连续性的本质。
2. 什么是光电效应?光电效应有什么规律?爱因斯坦是如何解释光电效应的?答:当一定频率的光照射到金属上时,有大量电子从金属表面逸出的现象称为光电效应;光电效应的规律:a.对于一定的金属材料做成的电极,有一个确定的临界频率?0,当照射光频率0时,无论光的强度有多大,不会观测到光电子从电极上逸出;b.每个光电子的能量只与照射光的频率有关,而与光强无关;c.当入射光频率0时,不管光多微弱,只要光一照,几乎立刻?10?9s观测到光电子。
爱因斯坦认为:(1)电磁波能量被集中在光子身上,而不是象波那样散布在空间中,所以电子可以集中地、一次性地吸收光子能量,所以对应弛豫时间应很短,是瞬间完成的。
(2)所有同频率光子具有相同能量,光强则对应于光子的数目,光强越大,光子数目越多,所以遏止电压与光强无关,饱和电流与光强成正比。
(3)光子能量与其频率成正比,频率越高,对应光子能量越大,所以光电效应也容易发生,光子能量小于逸出功时,则无法激发光电子。


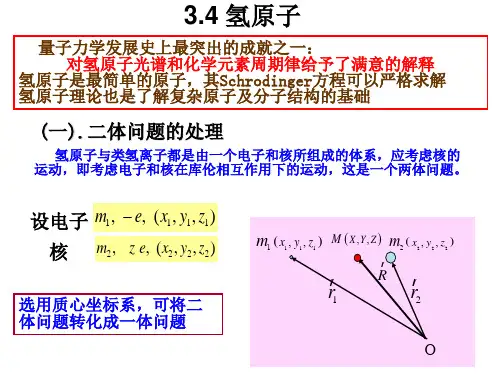
第十一章 原子与激光§11.1 氢原子的能级和能量本征函数 一、能量的本征方程、本征值与本征态 氢原子的哈密顿算子为(),r U mH +∇-=222ˆ 其中()r e r U 024πε-=其能量本征方程是nlmn nlm E H ψψ=ˆ 解得能量本征值222024132n me E n επ-=及对应本征态()()()ϕφθψm lm nl nlm r R Ξ=其中,n 为主量子数、l 为轨道量子数、m 为磁量子数,记nlnlrR =χ是径向的概率密度幅、Ξθ(lm )是θ横向的概率密度幅、()ϕϕφim m e =是φ方向的概率密度幅。
氢原子能量本征方程的处理思路:1、将直角坐标系转换到球坐标系]sin )(sin sin )([22222221122φθθθθθμμ∂+∂∂+∂∂-=∇-r r r r 2、在质心系中处理:等效准粒子mM Mm+=μ绕质心粒子m M +的运动3、分离变量)()()(),,(φθφθψm lm nl nlm r R r ΦΞ=4、量子数m l n ,,由波函数的标准化条件得到)()()(),,(φθφθψm lm nl nlm r R r ΦΞ=是驻波由原子定态的稳定性,氢原子束缚能量本征态一定是一个概率密度幅驻波,例如:230102a r e a r //-=χ 在0=r 和r →∞处有一个节点,n =1,l=0,节点数2=r N 。
20223021621a r e a r a //-=χ 在r = 0及r →∞各有一个节点,n =2,l=1,2=r N 。
()020302022a r e a r a r /-⎪⎪⎭⎫ ⎝⎛-=χ 在r =0,r =2a 0及r →∞各有一个节点,n =2,l=0,3=r N 。
它们都是驻波。
量子数n ,l 的节点数r N 有关系:l n N r -+=1 (11-1.1)即n 、l 决定了能量本征态的径向概率密度幅驻波的节点数,图11-1-3,给出一些nl χ驻波及节点分布。
《结构化学》第二章习题2001 在直角坐标系下, Li 2+ 的Schr ödinger 方程为________________ 。
2002 已知类氢离子 He +的某一状态波函数为:()022-023021e 222241a r a r a ⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛π 则此状态的能量为 )(a , 此状态的角动量的平方值为 )(b , 此状态角动量在 z 方向的分量为 )(c , 此状态的 n , l , m 值分别为 )(d , 此状态角度分布的节面数为 )(e 。
2003已知 Li 2+ 的 1s 波函数为03130s1e 27a r -α⎥⎦⎤⎢⎣⎡π=ψ (1)计算 1s 电子径向分布函数最大值离核的距离;(2)计算 1s 电子离核平均距离; (3)计算 1s 电子概率密度最大处离核的距离。
(10!d e +∞-=⎰n ax n a n x x )2004 写出 Be 原子的 Schr ödinger 方程 。
2005 已知类氢离子 He +的某一状态波函数为 ()02-023021e 222241a r a r a ⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛π则此状态最大概率密度处的 r 值为 )(a , 此状态最大概率密度处的径向分布函数值为 )(b , 此状态径向分布函数最大处的 r 值为 )(c 。
2006 在多电子原子中, 单个电子的动能算符均为2228∇π-mh 所以每个 电子的动能都是相等的, 对吗? ________ 。
2007 原子轨道是指原子中的单电子波函数, 所以一个原子轨道只能容纳一个电子,对吗? ______ 。
2008 原子轨道是原子中的单电子波函数, 每个原子轨道只能容纳 ______个电子。
2009 H 原子的()υr,θψ,可以写作()()()υθr R ΦΘ,,三个函数的乘积,这三个函数分别由量子数 (a) ,(b), (c) 来规定。
量子力学中的氢原子和波函数的密度量子力学是一门研究微观物质和能量的科学,它在20世纪初由一些杰出的科学家,如普朗克、玻尔和薛定谔等人所创立。
量子力学的基本原理和概念被广泛应用于物理、化学、生物和工程学等领域,它已经成为现代科学的基石之一。
在量子力学理论中,氢原子是研究的重点之一。
氢原子是最简单的原子,由一个质子和一个电子组成。
根据薛定谔方程,氢原子的波函数可以通过解析方法得到。
波函数描述了氢原子在不同位置和动量下的概率分布,它是描述微观粒子行为的数学函数。
在氢原子中,波函数的密度分布对于理解原子结构和化学反应具有重要意义。
首先,让我们讨论氢原子的波函数及其密度分布。
氢原子的波函数通常由球坐标系来描述,它包含了径向部分和角向部分。
径向部分描述了原子的位置,角向部分描述了原子的方向。
波函数的模方给出了粒子在不同空间点被测到的概率密度。
在标准的氢原子波函数中,第一个量子数n决定了波函数的主要特征。
主量子数n越大,波函数的径向部分在原子核周围的振动更加复杂。
而角向部分则由两个量子数l和m决定。
量子数l决定了角动量的大小,量子数m决定了角动量在空间中的方向。
角向部分的形状决定了波函数的轨道形状。
通过计算波函数的模方,我们可以得到氢原子中电子在不同位置的概率分布情况。
由于氢原子的波函数具有球对称性,电子的概率分布也将具有球对称性。
这意味着在氢原子中,电子更有可能分布在离原子核较远的区域,而几乎没有几率在原子核附近出现。
根据波函数的密度分布,我们可以绘制出氢原子的电子云图。
电子云图以原子核为中心,展示了电子存在的区域。
电子云图可以帮助我们理解原子的形状和大小。
对于氢原子来说,电子云图呈现出球对称的形状。
除了电子云图,我们还可以通过波函数的其他性质来揭示氢原子的特性。
例如,波函数的平均值给出了氢原子的位置和动量的期望值。
位置算符和动量算符作用在波函数上,得到的数值可以给出氢原子在不同状态下的平均位置和动量。
此外,我们还可以利用波函数的密度分布来研究氢原子的能级结构。