下载文档原格式
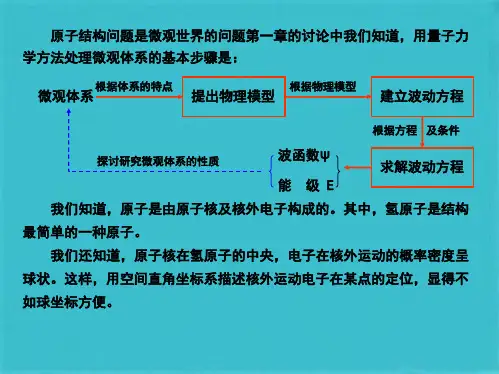
氢原子是所有原子中最简单的原子，它核外仅有一个电子，电子在核外运动时的势能，只决定于核对它的吸引，它的Schrödinge r方程可以精确求解。
能够精确求解的还有类氢离子，如He+、Li2+离子等。
为了求解方便，要把直角坐标表示的ψ(x，y，z) 改换成球极坐标表示的ψ(r,θ，φ)，二者的关系如图8-3所示：r表示P点与原点的距离，θ、φ称为方位角。
x = r sinθcosφy = r sinθsinφz = r cosθ解出的氢原子的波函数ψn,l,m(r,θ，φ)及其相应能量列于表8-1中。
图8-3 直角坐标转换成球极坐标表8-1氢原子的一些波函数及其能量cos cossin sinsin sin* A1、A2、A3、B均为常数为了方便起见，量子力学借用Bohr N H D理论中“原子轨道” (atomic orbit)的概念，将波函数仍称为原子轨道(atomic orbital)，但二者的涵义截然不同。
例如：Bohr N H D认为基态氢原子的原子轨道是半径等于52.9 pm的球形轨道。
而量子力学中，基态氢原子的原子轨道是波函数ψ1S(r,θ,φ)=A1e-Br，其中A1 和B均为常数，它说明ψ1S在任意方位角随离核距离r改变而变化的情况，它代表氢原子核外1s电子的运动状态，但并不表示1s电子有确定的运动轨道。
1s电子具有的能量是-2.18³10-18J。
氢原子核外电子的运动状态还有许多激发态，如ψ2s(r,θ,φ)、(r,θ,φ)等，相应的能量是-5.45³10-19J。
要解出薛定谔方程的ψ和E，必须要满足一定的条件，才能使解是合理的，因此，在求解过程中必需引进n , l , m三个量子数。
这三个参数的取值和组合一定时，就确定了一个波函数。
三个量子数的取值限制和它们的物理意义如下：常用符号n表示。
它可以取非零的任意正整数，即1，2，3 …n 。
它决定电子在核外空间出现概率最大的区域离核的远近，并且是决定电子能量高低的主要因素。
第二节氢原子的波函数波函数氢原子是所有原子中最简单的原子，它核外仅有一个电子，电子在核外运动时的势能，只决定于核对它的吸引，它的Schrödinger方程可以精确求解。
能够精确求解的还有类氢离子，如He+、Li2+离子等。
为了求解方便，要把直角坐标表示的ψ(x，y，z) 改换成球极坐标表示的ψ(r,θ，φ)，二者的关系如图8-3所示：r表示P点与原点的距离，θ、φ称为方位角。
x = r sinθcosφy = r sinθsinφz = r cosθ解出的氢原子的波函数ψn,l,m(r,θ，φ)及其相应能量列于表8-1中。
图8-3 直角坐标转换成球极坐标表8-1氢原子的一些波函数及其能量轨道ψn，l，m(r,θ, φ)R n，l (r)Y l，m (θ, φ)能量/J1sA1e-B rA1e-B r-2.18×10-182sA2re-B r/2A2re-B r/2-2.18×10-18/222p zA3re-B r/2cosθA3re-B r/2cosθ-2.18×10-18/222p xA3re-B r/2sinθcosφA3re-B r/2sinθcosφ-2.18×10-18/222p yA3re-B r/2sinθsinφA3re-B r/2sinθsinφ-2.18×10-18/22* A1、A2、A3、B均为常数为了方便起见，量子力学借用Bohr N H D理论中“原子轨道”(atomic orbit)的概念，将波函数仍称为原子轨道(atomic orbital)，但二者的涵义截然不同。
例如：Bohr N H D认为基态氢原子的原子轨道是半径等于52.9 pm的球形轨道。
而量子力学中，基态氢原子的原子轨道是波函数ψ1S(r,θ,φ)=A1e-Br，其中A1和B均为常数，它说明ψ1S在任意方位角随离核距离r改变而变化的情况，它代表氢原子核外1s电子的运动状态，但并不表示1s电子有确定的运动轨道。
