轴对称画图
- 格式:ppt
- 大小:2.22 MB
- 文档页数:18







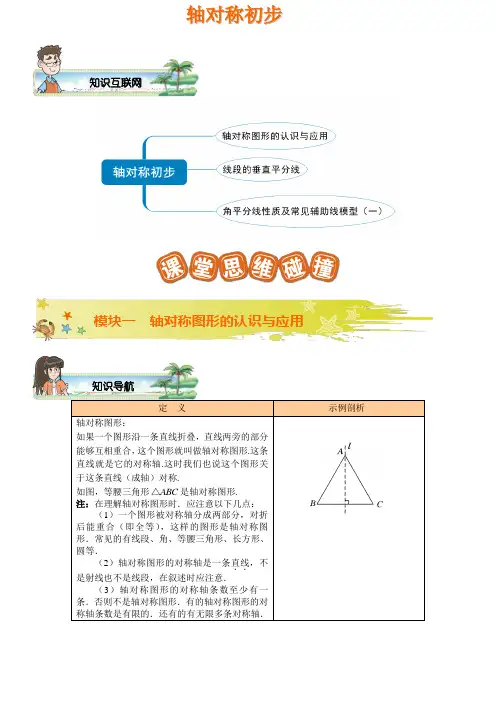
定 义示例剖析轴对称图形:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形.这条直线就是它的对称轴.这时我们也说这个图形关于这条直线(成轴)对称.如图,等腰三角形ABC △是轴对称图形.注:在理解轴对称图形时.应注意以下几点:(1)一个图形被对称轴分成两部分,对折后能重合(即全等),这样的图形是轴对称图形.常见的有线段、角、等腰三角形、长方形、圆等.(2)轴对称图形的对称轴是一条直线..,不是射线也不是线段,在叙述时应注意.(3)轴对称图形的对称轴条数至少有一条.否则不是轴对称图形.有的轴对称图形的对称轴条数是有限的.还有的有无限多条对称轴.知识互联网知识导航模块一 轴对称图形的认识与应用轴对称初步两个图形轴对称:把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做对称点.如图,ABC△与'''A B C△关于直线l对称,l叫做对称轴.A和'A,B和'B,C和'C是对称点.注:把成轴对称的两个图形看成一个整体,它就是一个轴对称图形.轴对称的性质:1.关于一条直线轴对称的图形全等;2.对称点连成的线段被对称轴垂直平分.【例1】⑴在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是()A B C D⑵在3×3的正方形格点图中,有格点△ABC和△DEF,且△ABC和△DEF关于某直线成轴对称,请在下面给出的图中画出4个这样的△DEF.A BCA BCA BCCBA⑶正六边形是轴对称图形,它有条对称轴.⑷下列图形中对称轴最多的是()A.圆B.正方形C.等腰三角形D.线段⑸判断下列图形是否为轴对称图形?如果是,说出它有几条对称轴.⑹已知两条互不平行的线段AB和A′B′关于直线l对称,AB和A′B′所在的直线交于点P,下面四个结论:①AB=A′B′;②点P在直线l上;③若A、A′是对应点,则直线l垂直平分线段AA′;④若B、B′是对应点,则PB=PB′,其中正确的是()夯实基础A .①③④B .③④C .①②D .①②③④【例2】 ⑴ 图1的长方形ABCD 中,E 点在AD 上,且∠ABE =30°.分别以BE 、CE 为折线,将A 、D 向BC 的方向折过去,图2为对折后A 、B 、C 、D 、E 五点均在同一平面上的位置图.若图2中,∠AED =15°,则∠BCE 的度数为( )A .30°B .32.5°C .35°D .37.5°⑵如图是一台球桌面示意图,图中小正方形的边长均相等,黑球放在如图所示的位置,经白球撞击后沿箭头方向运动,经桌边反弹最后进入球洞的序号是( ) A .① B .② C .③ D .④⑶ 已知30AOB ∠=°,点P 在AOB ∠内部,1P 与P 关于OB 对称,2P 与P 关于OA 对称,则1P ,O ,2P 三点确定的三角形是( )A .直角三角形B .钝角三角形C .腰底不等的等腰三角形D .等边三角形定 义示例剖析线段的垂直平分线:经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线,也称之为中垂线.EDC BA 如图,若AC BC =,AB CD ⊥,则直线DE 是线段AB 的垂直平分线.模块二 线段的垂直平分线知识导航能力提升图2图1ABCD EED④②线段垂直平分线的性质:线段垂直平分线上的点与这条线段两个端点的距离相等.EDC BA如图,已知直线DE 是线段AB 的垂直平分线,则DA DB =.线段的垂直平分线的判定:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.EDC BA如图,若DA DB =,则点D 在线段AB 的垂直平分线上.【例3】 ⑴ 如何用圆规与直尺作线段AB 的垂直平分线?⑵ 证明:线段的垂直平分线上的点与这条线段两个端点的距离相等(线段垂直平分线的性质).⑶ 证明:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上(线段垂直平分线的判定).【例4】 ⑴ 如下图1,在△ABC 中,DE 是AC 的中垂线,AE =3cm ,△ABD 得周长为13cm ,则△ABC 的周长是 .⑵ 如下图2,BD 垂直平分线段AC ,AE ⊥BC ,垂足为E ,交BD 于P 点,PE =3cm ,则P 点到直线AB 的距离是 .夯实基础⑶ 如下图3,在ABC △中,90A ∠=︒,:2:3ABD DBE ∠∠=,DE BC ⊥,E 是BC 的中点,求C ∠的度数.图3图2图1ED CBAPE DCBAED CBA【例5】 ABC △的两边AB 和AC 的垂直平分线分别交BC 于点D 、E ,⑴若BC =8,求△ADE 的周长;⑵若150BAC DAE ∠+∠=︒,求BAC ∠.定 义示例剖析角平分线的性质定理:在角的内部平分线上的点到这个角的两边的距离相等.DFEO CBA如图,若射线OC 是∠AOB 的角平分线,则DE=DF .角平分线的判定定理:在角的内部到一个角两边距离相等的点在这个角的平分线上.DFEOCB A能力提升知识导航模块三 角平分线性质及常见辅助线模型(一)H FEDCB A如图,若DE=DF ,则OC 是∠AOB 的角平分线.角平分线的两种基本模型1. 点垂线,垂两边,对称全等要记全A BCDO12E已知:12∠=∠,CD OA ⊥,作CE OB ⊥于E ,则OCD OCE △≌△.2.角平分线+平行线,等腰三角形必呈现321OD CBA已知:12∠=∠,CD OB ∥交OA 于D ,则ODC △为等腰三角形(即OD CD =).【教师铺垫】证明:⑴ 角平分线上的点到这个角的两边的距离相等(角平分线的性质定理).⑵ 在角的内部到一个角两边距离相等的点在这个角的平分线上(角平分线的判定定理).⑶ 三角形的三条内角平分线交于一点.(此点称之为三角形的内心).⑷ 三角形的内心到三边的距离相等.(三角形内心性质).夯实基础CPB ANM O CPBANMO【例6】 ⑴ 如图,已知ABC △的周长是21,OB ,OC 分别平分ABC ∠和ACB ∠,OD BC ⊥于D ,且3OD =,求ABC △的面积.⑵ 如图所示,2AB AC =,1∠2=∠,DA DB =. 求证:DC AC ⊥.【例7】 如图,在△ABC 中,AD 是∠BAC 平分线,AD 的垂直平分线分别交AB 、BC 延长线于F 、E ,求证:⑴∠EAD =∠EDA ;⑵DF ∥AC ;⑶∠EAC =∠B .训练1. D 为BC 中点,DE BC ⊥交BAC ∠的平分线于点E ,EF AB ⊥于F ,EG AC ⊥于G .求证:BF CG =.思维拓展训练(选讲)能力提升21ADCBA B C DE F O G ODCBAFAGEDCB训练2.已知:如图,ABC∠及两点M、N.求作:在平面内找一点P,使得PM PN=,且P点到ABC∠两边所在的直线的距离相等.NMBCA训练3.如图,在ABC△中,BD、CD分别平分ABC∠和ACB∠.DE AB FD AC∥,∥.如果6BC=,求DEF△的周长.训练4.已知:如图,在POQ∠内部有两点M、N,MOP NOQ∠=∠.⑴画图并简要说明画法:在射线OP上取一点A,使点A到点M和点N的距离和最小;在射线OQ上取一点B,使点B到点M和点N的距离和最小;⑵直接写出AM AN+与BM BN+的大小关系.知识模块一轴对称图形的认识与应用课后演练【演练1】⑴下面四个图形中,从几何图形的性质考虑,哪一个与其他三个不同?请指出这个图形,并简述你的理由.实战演练FEDCBAMNQO④③②①答:图形__________;理由是__________.⑵ 画出下图所示的轴对称图形的对称轴:⑶ 如图是奥运会会旗上的五环图标,它有( )条对称轴.A .1B .2C .3D .4⑷ 下列图形中,不是轴对称图形的是( ).A .角B .等边三角形C .线段D .不等边三角形⑸ 如图,它们都是对称的图形,请观察并指出哪些是轴对称图形,哪些图形成轴对称.【演练2】 如图,把ABC △纸片沿DE 折叠,当点A 落在四边形BCED 的外部时,则A ∠与1∠和2∠之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( ). A .12A ∠=∠-∠B .212A ∠=∠-∠C .3212A ∠=∠-∠D .()3212A ∠=∠-∠知识模块二 线段的垂直平分线 课后演练【演练3】 如图,已知40AOB ∠=︒,CD 为OA 的垂直平分线,求ACB ∠的度数.21E ADCBO DC BA知识模块三角平分线性质及常见辅助线模型(一)课后演练【演练4】如图,BD CD=,90ABD ACD∠=∠=°,点E、F分别在AB、AC 上,若ED平分BEF∠.①求证:FD平分EFC∠;②求证:EF BE CF=+.【演练5】证明:三角形一个内角的平分线与另外两个外角的平分线交于一点.FEDC BA。



第五章轴对称的性质与作图本章进步目标★★★★★☆Level 5通过对本节课的学习,你能够:1.对轴对称的性质与判定达到【高级理解】级别;2.对垂直平分线与角平分线的相关概念达到【初级运用】级别;3.对路径最短问题达到【高级理解】级别。
VISIBLE PROGRESS SYSTEM进步可视化教学体系据说,古希腊有一位聪明过人的学者,名叫海伦。
有一天,一位将军向他请教了一个问题:从A地出发到河边饮马,然后再去B地,走什么样的路线最短?如何确定饮马的地点?提起路线最短的问题,大家知道,连结两点之间的所有线中,最短的是线段。
这个题中马走的是一条折线。
这该怎么办呢?海伦的方法是这样的:取A关于河岸的对称点A',连结A'B,与河岸线相交于C,则C点就是饮马的地方。
将军只要从A出发,沿直线走到C,饮马之后,再由C沿直线走到B,所走的路程就是最短的。
如果将军在河边的另外任一点C'饮马,所走的路程就是AC'+C'B,但是,AC'+C'B=A'C'+C'B>A'B=A'C+CB=AC+CB.可见,在C点外任何一点C'饮马,所走的路程都要远一些.这里有几点需要说明:(1)由作法可知,河流l相当于线段AA'的中垂线,所以AD=A'D。
(2)由上一条可知,将军走的路程就是AC+BC,就等于A'C+BC,而两点确定一线,所以C点为最优。
年轻朋友们喜欢打台球,实际上打台球无时无刻都需要应用海伦的妙法。
下面我们看一个有关打台球的实例。
若在矩形的球台上,有两个球在M和N的位置上。
假如从M打出球,先触及AB边E点,弹出后又触到CB边F点,从CB边再反射出来。
问用怎样的打法,才能使这个球反射后正好撞上在N点放置的球?具体做法是:先作M关于AB的对称点M’,再作N关于BC的对称点N’,那么M’N’和BC的交点为E,F;E、F就是球和各边的撞击点。
圆的专题三:无刻度直尺画图中的轴对称1.如图,在△AB C中AB=AC,D点为边BC的中点,(1)如图1,点P为边AB上面任意一点,请在AC上找一点Q,使得AQ=AP,保留作图痕迹,不用证明.图1图2图3图4【变式训练1】如图2,连AD,在AD上面画一点H,使得∠AHP=90°;【变式训练2】如图3,在AC上面画一点R,PR∥BC.(2)如图4,点F为线段BD上任意一点,请在CD上找一点G,使得CG=BF,保留作图痕迹,不用证明.【利用三线交于同一点解题】2.在三角形中,三边的高或高的延长线交于一点,这个交点我们叫做三角形的垂心,请根据上述性质,完成下列各题,不用说明理由,保留作图痕迹即可.(1)如图1,△ABC的各顶点在以AB为直径的半圆上,则△ABC的垂心是;(2)如图2,只用不带刻度的直尺(不能用圆规),从半圆外的C点向直径AB作垂线(不写画法);(3)如图3,作图工具要求不变,从C点向直径AB的延长线作垂线(不写画法);图1图2图33.请用无刻度直尺完成下列作图,不写画法,保留画图痕迹.(用虚线表示画图过程,实线表示画图结果),如图4,BC是⊙O的直径,A是⊙O内一点,画△ABC的高AD.【利用轴对称找相等的圆周角,再得弦相等】【2021元调】4.如图是由小正方形构成的6×6网格,每个小正方形的顶点叫做格点.⊙P经过A,B 两个格点,仅用无刻度的直尺在给定网格中按要求画图(画图过程用虚线表示,画图结果用实线表示).(1)在图(1)中,⊙P经过格点C,画圆心P,并画弦BD,使BD平分∠ABC;(2)在图(2)中,⊙P经过格点E,F是⊙P与网格线的交点,画圆心P,并画弦FG,使FG=FA.5.(1)如图1,已知:A、B为格点,C为圆上一点,求作∠ACB的平分线CD,交圆于点D;(2)如图2,已知:A、B、D均为格点,P为圆与格线的交点,在圆上求作一点B,使∠CAP=∠BAP.(3)A、P、B均为格点,C为圆与格线的交点,在圆上求作一点M,使得AC=MC.图1图2图36.如图,在5×5的网格中,△ABC的三个顶点都在格点上.用无刻度的直尺作图:(1)在图1中画出一条恰好平分△ABC周长的直线l;(2)在图2中画出△ABC的外接圆的一条切线AD;(3)在图2中画出△ABC关于直线AB对称的△ABE;(4)在图2中若CE交AB于点H,画出平行四边形HACF.图1图2【利用圆周角定理或者圆内接四边形对角互补的性质画图】7.(本题8分)请仅用无刻度的直尺画图,不写作法,保留画图痕迹.(1)如图1,点O是等腰△ABC底边BC的中点,E是AB上一点,请在AC上作出点F,使EF∥BC;(2)如图2,△ABC为⊙O的内接三角形,请在AB,AC上分别作出点M,N,使MN∥BC;8.(本题8分)如图,已知A,B,C均在⊙O上,请用无刻度的直尺作图.(1)如图1,若点D是AC的中点,试画出∠B的平分线;(4分)(2)若∠A=42°,点D在弦BC上,在图2中画出一个含48°角的直角三角形.(4分)9.作图题:⊙O上有三个点A,B,C,∠BAC=70°,请画出要求的角,并标注.(1)画一个140°的圆心角;(2)画一个110°的圆周角;(3)画一个20°的圆周角.【武昌区七校】10.图1、图2是正八边形,DH 是对角线,图3是圆内接正五边形,请用无刻度的直尺,完成下列要求(辅助线画虚线,要求所作的线画实线):(1)如图1,在DH 上取点P ,使得PA =PB ;(2)如图2,在DH 上取点P ,使得PA+PB 最小;(3)如图3,在圆上取点P ,使得圆周角∠PAB =126°.11.【洪山区】(1)如图1,在7×7的正方形网格中,每个小正方形的边长为1,小正方形的顶点叫做格点,△ABC 的顶点在格点上,过点A 画一条直线平分△ABC 的面积(2)如图2,点E 在正方形ABCD 的内部,且EB=EC,过点E 画一条射线平分∠BEC(3)如图3,点A、B、C 均在⊙O 上,且∠BAC=120°,在优弧BC 上画M、N 两点,使∠MAN=60°【三寄宿】12.请用无刻度直尺按要求画图,不写画法,保留画圏痕迹.(用虚线表示画图过程,实线表示画图结果)(1)如图1,在正方形网格中,有一圆经过了两个小正方形的顶点A,B,请画出这个圆的一条直径;(2)如图2, ABC 内接于⊙O ,∠BAC=50°,在图中画一个含有50°的直角三角形;(3)如图3,BA,BD 是⊙O 中的两条弦,C 是BD 上一点,∠BAC=50°,在图中画一个含有50°角的直角三角形;F G H AB C D E 图1F G H A B C D E图2A C B D O E 图3。
1 一,画图:1.如图,在正方形网格上有一个△ABC. (1)作△ABC 关于直线MN 的对称图形(不写作法); (2)若网格上的最小正方形的边长为1,求△ABC 的面积.2. (1) 如图所示编号为①、②、③、④的四 个三角形中,关于y 轴对称的两个三角形的编号为 ;关于坐标原点O 对称的两个三角形的编号为 ;(2) 在图4中,画出与△ABC 关于x 轴对称的△A 1B 1C 13、画出线段AB 的中垂线。
4、画出∠AOB 的角平分线。
5、在AB 上找一点P ,使P 到6、在直线MN 上找一点P 点,使PM 、N 两点的距离相等。
到射线OA 和OB 的距离相等。
(4)(3)(2)(1)yx -1-2-4-3-5-1-2-4-5-31243512435O y x -1-2-4-3-5-1-2-4-5-31243512435C B AOAB C MN 第21题A B BO A A B M N B O A N M2 7、如图,A 、B 、C 三点表示三个工厂,要建一个供水站,使它到这三个工厂的距离相等。
8、如图,l 1、l 2交于A 点,P 、Q 的位置如图所示,试确定M 点,使它到l 1、l 2的距离相等,且到P 、Q 两点的距离也相等。
9、画出以下图形的对称轴。
10、画出以下图形的轴对称图形。
11、在铁路a 的同侧有两个工厂A 和B ,要在铁路边建一货场C ,使A 、B 两厂到货场C 的距离和最小,试在图上作出C 。
二,轴对称图形:1. 下列图形中,是轴对称图形的有 ( )A.1个B.2个C.3个D.4个2.从镜子中看到钟的时间是8点25分,正确的时间应是几点?( )A.3点25分B.3点30分C.3点35分D.3点45分3. 下列图案中,有且只有三条对称轴的是( )AB C A Q P l 2 l 1 Aa BA BC D A Bl l A B C D4. 下列图形中,是轴对称图形的有()个.新-课-①角;②线段;③等腰三角形;④等边三角形;⑤三角形.A.1个B.2个C. 3个D.45.观察下列图案,是轴对称图形的是()6.下列数中,成轴对称图形的有()个A.1 B.2 C.3 D.47.如图所示,将一张正方形纸片经过两次对折,并剪出一个菱形小洞后展开铺平,得到的图形是().8.已知点P(-2,1),那么点P关于x轴对称的点P 的坐标是()A.(-2,1)B.(-2,-1)C.(-1,2)D.(2,1)9.下列轴对称图形中,对称轴条数最少的是()A.等腰直角三角形B.正方形C.等边三角形D.长方形10.如图2所示是一张画有小白兔的卡片,卡片正对一面镜子,这张卡片在镜子里的影像是下列各图中的().图2 A B C D11.(2013•徐州)若等腰三角形的顶角为80°,则它的底角度数为()A.80°B.50° C.40° D.20°12.(2013•新疆)等腰三角形的两边长分别为3和6,则这个等腰三角形的周长为()A.12 B.15 C.12或15 D.1813.(2013•武汉)如图,△ABC中,AB=AC,∠A=36°,BD是AC边上的高,则∠DBC的度数是()A.18°B.24° C.30° D.36°14.(2013•钦州)等腰三角形的一个角是80°,则它顶角的度数是()A.80°B.80°或20°C.80°或50°D.20°15.(2013•淮安)若等腰三角形有两条边的长度为3和1,则此等腰三角形的周长为()34 C D A B A .5B .7C .5或7D .6三,经典练习:1. △ABC 中,AB=AC ,BC=5cm ,作AB 的垂直平分线交另一腰AC 于D ,连结BD ,如果△BCD 的周长17cm ,则腰长为( )A .12cm ;B .6cm ;C .7cm ;D .5cm .2.如图,已知,△ABC 中AQ=PQ ,PR=PS ,PR ⊥AB 于R ,PS ⊥AC 于S ,则三个结论①AS=AR ;②QP ∥AR ;③△BRP ≌△QSP 中( )A .全部正确B .仅①和②正确C .仅①正确D .仅①和③正确3.已知,如图,∠C=90°,若∠1=∠2,BC=10,BD=6,则D 到AB 边的距离是4.如图,∠C=90°,DE 垂直平分AB ,∠1:∠2 = 2:3,则∠BAC= 度5. 如图,在ABC △中,90C ∠=,AD 平分CAB ∠,8cm 5cm BC BD ==,,那么D 点到直线AB 的距离是 cm .6.如图,在Rt △ABC 中,∠C=90°,∠A=30°,BD 是∠ABC 的平分线,若BD=10,则CD=7.如图,△ABC 中,AB=AC ,DE 是AB 的垂直平分线, AB=8,BC=4,∠A=36°,则∠DBC= ,△BDC 的周长C △BDC = .8.如图,△ABC 中,AB=AC,∠BAC=100°,AD ⊥BC 于D,求∠B,∠CAD 的度数.(9分)21D CB A 21 E D C B A第6题 第7题 第5题 B5。