轴对称作图

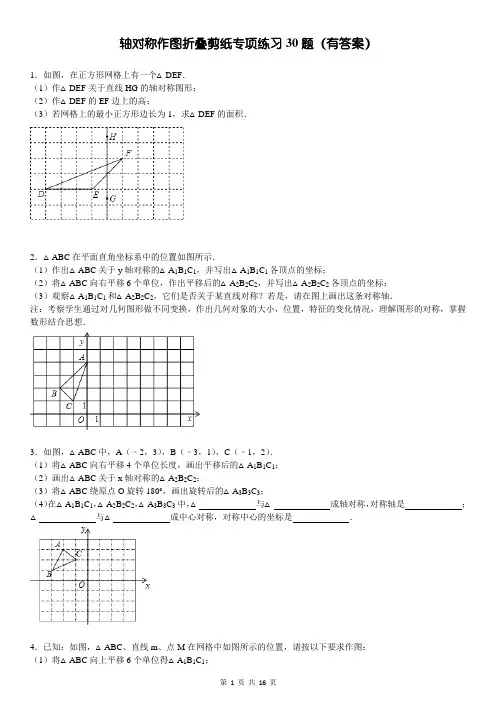
轴对称作图折叠剪纸专项练习30题（有答案）1．如图，在正方形网格上有一个△DEF．（1）作△DEF关于直线HG的轴对称图形；（2）作△DEF的EF边上的高；（3）若网格上的最小正方形边长为1，求△DEF的面积．2．△ABC在平面直角坐标系中的位置如图所示．（1）作出△ABC关于y轴对称的△A1B1C1，并写出△A1B1C1各顶点的坐标；（2）将△ABC向右平移6个单位，作出平移后的△A2B2C2，并写出△A2B2C2各顶点的坐标；（3）观察△A1B1C1和△A2B2C2，它们是否关于某直线对称？若是，请在图上画出这条对称轴．注：考察学生通过对几何图形做不同变换，作出几何对象的大小，位置，特征的变化情况，理解图形的对称，掌握数形结合思想．3．如图，△ABC中，A（﹣2，3），B（﹣3，1），C（﹣1，2）．（1）将△ABC向右平移4个单位长度，画出平移后的△A1B1C1；（2）画出△ABC关于x轴对称的△A2B2C2；（3）将△ABC绕原点O旋转180°，画出旋转后的△A3B3C3；（4）在△A1B1C1，△A2B2C2，△A3B3C3中，△_________与△_________成轴对称，对称轴是_________；△_________与△_________成中心对称，对称中心的坐标是_________．4．已知：如图，△ABC、直线m、点M在网格中如图所示的位置，请按以下要求作图：（1）将△ABC向上平移6个单位得△A1B1C1；（2）作出△ABC关于直线m的轴对称图形△A2B2C2；（3）作出△A2B2C2绕点M顺时针旋转90°的图形△A3B3C3．5．△ABC在平面直角坐标系中如图所示，（1）作出△ABC关于x轴对称的图形△A1B1C1；若P（a，b）是△ABC内一点，请用a，b表示出点P关于x轴对称的点P1的坐标；（2）作出△ABC关于原点对称的图形△A2B2C2，写出点C2的坐标．（3）△A2B2C2能否由△A1B1C1通过某种变换而得到？若能，请指出是何种变换．6．在平面直角系中，已知△ABC和△DEF的顶点分别为A（1，0）、B（3，0）、C（2，1）、D（4，3）、E（6，5）、F（4，7）．按下列要求画图：（1）画出△ABC以点O为位似中心，在y轴异侧放大2倍后得到的△A1B1C1，并写出点C1的坐标；（2）画出△A1B1C1关于x轴的对称图形△A2B2C2．并写出点C2的坐标；（3）指出△A2B2C2经过哪些变换，可以与△DEF拼成一个正方形．7．作图题（1）如图1，作出△ABC关于直线l的对称图形；（2）“西气东输”是造福子孙后代的创世纪工程．现有两条高速公路和A、B两个城镇（如图2），准备建立一个燃气中心站P，使中心站到两条公路距离相等，并且到两个城镇距离相等，请你画出中心站位置．8．（1）如图，作出△ABC关于直线l的对称图形；（2）“西气东输”是造福子孙后代的创世纪工程．现有两条高速公路和A、B两个城镇（如图），准备建立一个燃气中心站P，使中心站到两条公路距离相等，并且到两个城镇距离相等，请你画出中心站位置．9．如图，C、D、E、F是一个长方形台球桌的4个顶点，A、B是桌面上的两个球，怎样击打A球，才能使A球撞击桌面边缘CF后反弹能够撞击B球？请画出A球经过的路线，并写出作法．10．如图，直线m是一个轴对称图形的对称轴，画出这个轴对称图形的另一半；若它是一个正五角星，那么它一共有几条对称轴？它的五个星角（最外围5个角）度数之和是多少度？11．把一张正方形纸片按如图①、图②对折两次后，得到图③，并在其中挖去一个三角形小孔，请你画出展开后的图形（折痕用虚线画出）．12．小明把一张长方形纸片对折两次，画上一个四边形，再剪去这个图形（镂空），展开长方形纸，得到如下的图案，设折痕为l1、l2、l3，观察图并填空：（1）图中有_________条对称轴；（2）四边形①与四边形②关于_________成轴对称，折痕l2既是_________与_________的对称轴，又是_________与_________的对称轴，整体上看也是_________与_________的对称轴；（3）若小明把纸片对折三次，展开后，得到的四边形有几个，有几条对称轴？13．如图所示，将三角形纸片ABC的一个角折叠，折痕为EF，若∠A=80°；∠B=68°；∠CFE=78°，求∠CEF的度数．14．如图，在△ABC中，点D是BC边上的一点，∠B=50°，∠BAD=30°，将△ABD沿AD折叠得到△AED，AE与BC 交于点F．（1）填空：∠AFC=_________度；（2）求∠EDF的度数．15．如图，在△ABC中，AD是BC边上的高，将△ABD沿AD折叠得到△AED，点E落在CD上，∠B=50°，∠C=30°．（1）填空：∠BAD=_________度；（2）求∠CAE的度数．16．如图，矩形ABCD，AB＞AD，E在AD上，将△ABE沿BE折叠后，A点正好落在CD上的点F．（1）用尺规作出E、F；（2）若AE=5，DE=3，求DF的长．17．如图所示，将矩形ABCD沿着直线BD折叠，使点C落在点C′，BC′交AD于点E，AD=8，AB=4．（1）求证：△BED是等腰三角形；（2）求△BED的面积．18．如图所示，在矩形ABCD中，已知BC=2AB，E是CD上一点，连接BE，将矩形沿直线BE折叠，使点C落在AD的F点上，连接CF，求∠DCF的度数．19．如图，请你用三种方法把左边的小正方形分别平移到右边三个图形中，使它成为轴对称图形．20．长方形具有四个内角均为直角，并且两组对边分别相等的特征．如图，把一张长方形纸片ABCD折叠，使点C 与点A重合，折痕为EF．（1）如果∠DEF=123°，求∠BAF的度数；（2）判断△ABF和△AGE是否全等吗？请说明理由．21．将矩形纸片ABCD沿着对角线AC折叠，使点B落在点E处．（1）EF和DF的大小关系如何？请说明理由．（2）若∠ACB=20，求∠EAF的度数．22．如图，将长方形纸片的两角分别折叠，使顶点B落在B′处，顶点A落在A′处，EC为折痕，点E、A′、B′在同一条直线上．（1）猜想折痕EC和ED的位置关系，并说明理由．（2）ED的反向延长线交CA交于F，若∠BED=35°，求∠AEF和∠A′EC的度数．23．如图，将一张长方形纸片ABCD先以FG为折痕斜折过去，使角的顶点A落在A′处，再把BF折过去，折痕为EF．若∠AFG=25°，则∠BFE的度数是多少？24．（1）如图1，把△ABC沿DE折叠，使点A落在点A’处，试探索∠1+∠2与∠A的关系．（不必证明）．（2）如图2，BI平分∠ABC，CI平分∠ACB，把△ABC折叠，使点A与点I重合，若∠1+∠2=130°，求∠BIC的度数；（3）如图3，在锐角△ABC中，BF⊥AC于点F，CG⊥AB于点G，BF、CG交于点H，把△ABC折叠使点A和点H 重合，试探索∠BHC与∠1+∠2的关系，并证明你的结论．25．如图，在Rt△ABC中，∠ACB=90゜，∠A=50゜，将其折叠，使点A落在边CB上A′处，折痕为CD．求∠A′DB 的度数．26．如图，把正方形ABCD对折，折痕为MN．把顶点D折到MN上的一点P上，折痕为CE，再把顶点A折到MN上的同一点，折痕为BF，请回答下列问题：（1）线段PC、PB与正方形的边长有什么关系？（2）∠CPB的度数是多少？（3）还能知道哪些角的度数？请指出来．27．如图，△AOB纸片沿CD折叠，若O′C∥BD，那么O′D与AC平行吗？请说明理由．28．如图，折叠长方形ABCD的一边AD，点D落在BC边的D′处，AE是折痕，已知AB=8cm，CD′=4cm，求AD的长．29．如图，已知△ABC中，∠BAC=140°，现将△ABC进行折叠，使顶点B、C均与顶点A重合，求∠DAE的度数．30．如图所示，已知O是∠APB内的一点，点M、N分别是O点关于PA、PB的对称点，MN与PA、PB分别相交于点E、F，已知MN=5cm，求△OEF的周长．参考答案：1．解：（1）如图所示，△D′E′F′即为所求作的△DEF关于直线HG的轴对称图形；（2）如图所示，DH为EF边上的高线；（3）△DEF的面积=×3×2=32．解：（1）各点坐标为：A1（0，4），B1（2，2），C1（1，1）（2）各点坐标为：A2（6，4），B2（4，2），C2（5，1）（3）△A1B1C1与△A2B2C2关于直线x=3轴对称3．解：（1）（2）（3）如图所示；（4）由图可知：△A2B2C2与△A3B3C3呈轴对称，且对称轴为y轴；△A1B1C1与△A3B3C3呈中心对称，且对称中心为（2，0）．故答案为：A2B2C2 ，A3B3C3，y轴；A1B1C1，A3B3C3，（2，0）．4．解：（1）如图所示：△A1B1C1即为所求；（2）如图所示：△A2B2C2即为所求；（3）如图所示：△A3B3C3即为所求．5．解：（1）△A1B1C1如图所示，点P1的坐标为（a，﹣b）；（2）△A2B2C2如图所示，点C2的坐标（2，0）；（3）△A2B2C2能由△A1B1C1通过变换得到，是关于y轴对称．6．解：（1）如图所示，△A1B1C1即为所求作的三角形，C1（﹣4，﹣2）；（2）如图所示，△A2B2C2即为所求作的三角形，C2（﹣4，2）；（3）如图，利用△A2B2C2关于x轴的对称图形△A1B1C1，向下平移1个单位，再绕点Q顺时针旋转90°，使B2A2与DF重合，可以与△DEF拼成一个正方形7．解：（1）如图1所示：（2）如图2所示，8．解：（1）如图所示：（2）如图所示：有两个P点．9．解：作点A关于直线CF对称的点G，连接BG交CF于点P，则点P即为A球撞击桌面边缘CF的位置10．解：所画图形如右所示：这个图形是一个五角星，它有5条对称轴；∵∠1+∠2=∠6，3+∠4=∠5，∠1+∠5+∠6=180°，∴∠1+∠2+∠3+∠4+∠7=180°，故它的五个星角（最外围5个角）度数之和是180度11．解：当正方形纸片两次沿对角线对折成为一直角三角形时，在直角三角形中间的位置上剪三角形形，则直角顶点处完好，即原正方形中间无损，且三角形关于对角线对称，三角形的AB边平行于正方形的边12.解：（1）3；（2）l1，②与③，①与④，①②与③④；（3）若小明把纸片对折三次，展开后得到的四边形有八个，有7条对称轴13．解：∵△ABC中，∠A=80°，∠B=68°，∴∠C=180°﹣80°﹣68°=32°，∵△AEF中，∠C=32°，∠CFE=78°，∴∠CEF=180°﹣32°﹣78°=70°14．解：（1）∵△ABD沿AD折叠得到△AED，∴∠BAD=∠DAF，∵∠B=50°∠BAD=30°，∴∠AFC=∠B+∠BAD+∠DAF=110°；故答案为110．（2）∵∠B=50°，∠BAD=30°，∴∠ADB=180°﹣50°﹣30°=100°，∵△ABD沿AD折叠得到△AED，∴∠ADE=∠ADB=100°，∴∠EDF=∠EDA+∠BDA﹣∠BDF=100°+100°﹣180°=20°15．解：（1）∵AD是BC边上的高，∠B=50°，∴∠BAD=180°﹣90°﹣50°=40°．故答案为：40；（2）解法一：∵△AED是由△ABD折叠得到，∴∠AED=∠B=50°，∵∠AED是△ACE的外角，∴∠AED=∠CAE+∠C，∴∠CAE=∠AED﹣∠C=50°﹣30°=20°．解法二：∵△AED是由△ABD折叠得到，∴∠EAD=∠BAD=40°，∴∠BAE=80°，∴∠CAE=180°﹣∠B﹣∠C﹣∠BAE=180°﹣50°﹣30°﹣80°=20°16．解：（1）作法：①作BF=BA交CD于F，②连BF作∠ABF的平分线，则点E、F为所求；（2）连接EF，由条件知：Rt△ABE≌Rt△FBE，∴EF=AE，又∵AE=5，DE=3，∠D=90°，∴DF===417．（1）证明：根据翻折的性质可得：∠2=∠3，又AD∥BC，∴∠1=∠3，∴∠1=∠2，△BED是等腰三角形，得证．（2）解：设ED=x，则AE=8﹣x，BE=ED=x，在Rt△ABE中，根据勾股定理有AB2+AE2=BE2，代入得：42+（8﹣x）2=x2，解得：x=5，S△BED=ED•AB==1018．解：∵将矩形沿直线BE折叠，使点C落在AD的F点上，∴BF=BC，EF=EC，∠EFB=∠BCD=90°，在Rt△ABF中，BF=BC，而BC=2AB，∴BF=2AB，∴∠AFB=30°，∴∠DFE=90°﹣30°=60°，∴∠DEF=30°，∵EF=EC，∴∠ECF=∠EFC，∴∠ECF=∠DEF=15°19．解：设计图案如下：20．解：（1）∵四边形ABCD是矩形，∴AB=CD，∠B=∠DAB=90°，AD∥BC．∴∠AEF=∠CFE．∵∠DEF+∠AEF=180°，且∠DEF=123°，∴∠AEF=57°，∴∠CFE=57°．∵四边形CDEF与四边形AGEF关于EF对称，∴四边形CDEF≌四边形AGEF∴∠G=∠C=∠D=∠GAF=90°．AG=CD，∠AFE=∠CFE．∴∠AFE=57°．∵∠BFA+∠AFE+∠CFE=180°，∴∠BFA=66°．∵∠BFA+∠BAF=90°，∴∠BAF=24°．答：∠BAF的度数为24°；（2）△ABF≌△AGE．∵AG=CD∴AB=AG．∵∠BAE=90°，∠GAF=90°，∴∠BAE=∠GAF，∴∠BAE﹣∠EAF=∠GAF﹣∠EAF，∴∠BAF=∠GAE．在△ABF和△AGE中，∴△ABF≌△AGE（ASA）21．解：（1）EF=DF，理由为：由折叠的性质得到△ABC≌△AEC，再由矩形的性质得到△ABC≌△ADC，∴△AEC≌△ADC，∠E=∠D=90°，∴∠DAC=∠ECA，∴AF=CF，在△AEF和△CDF中，，∴△AEF≌△CDF（AAS），则EF=DF；（2）∵AD∥BC，∴∠DAC=∠ACB=20°，∵在Rt△ABC中，∠B=90°，∠ACB=20°，∴∠BAC=∠EAC=60°，则∠EAF=∠EAC﹣∠DAC=40°22．解：（1）折痕EC和ED是垂直关系．∵EC和ED是折痕，理由：∴∠1=∠2，∠3=∠4，又∵∠1+∠2+∠3+∠4=180°，∴2（∠2+∠3）=180°，∴∠2+∠3=90°，即CE⊥ED，∴折痕EC和ED是垂直关系．（2）由（1）知CE⊥ED，∴∠2+∠3=90°，又∵∠2=∠1=35°，∴∠3=90°﹣∠1=90°﹣35°=55°，即∠A′EC=55°；∵ED的反向延长线交CA交于F，∴∠AEF=∠1=35°．23．解：∵△A′GF由△AGF翻折而成，四边形B′C′EF由四边形BCEF翻折而成，∴∠AFG=∠A′FG=25°，∠BFE=∠B′FE，∴∠BFE+∠B′FE=180°﹣（∠AFG+∠A′FG）=180°﹣50°=130°，∴∠BFE==65°．答：∠BFE的度数是65°24．解：（1）∠1+∠2=2∠A；（2）由（1）∠1+∠2=2∠A，得2∠A=130°，∴∠A=65°∵IB平分∠ABC，IC平分∠ACB，∴∠IBC+∠ICB=（∠ABC+∠ACB）=（180°﹣∠A）=90°﹣∠A，∴∠BIC=180°﹣（∠IBC+∠ICB），=180°﹣（90°﹣∠A）=90°+×65°=122.5°；（3）∵BF⊥AC，CG⊥AB，∴∠AFH+∠AGH=90°+90°=180°，∠FHG+∠A=180°，∴∠BHC=∠FHG=180°﹣∠A，由（1）知∠1+∠2=2∠A，∴∠A=（∠1+∠2），∴∠BHC=180°﹣（∠1+∠2）25．解：∵将△ACD折叠，使点A落在边CB上A′处，折痕为CD，∠ACB=90°，∴∠DCA=∠BCD=45°，∠CDA=∠CDA′，∴∠CDA=180°﹣∠DCA﹣∠A=180°﹣45°﹣50°=85°，∴∠CDA′=85°，∵∠BDC=∠A+∠DCA=50°+45°=95°，∴∠A′DB=∠BDC﹣∠A′DC=95°﹣85°=10°．26．解：（1）通过翻折变换的特点可知线段PC、PB与正方形的边长相等；（2）∵PC=PB=BC，∴∠CPB=60°；（3）由（2）可知：∠DCP=∠ABP=∠PEF=∠PFE=30°，∠PED=∠AFP=150°．27．解：O′D与AC平行．理由如下：∵O′C∥BD，∴∠2=∠4．∵∠2=∠1，∠3=∠4，∴∠3=∠1．∴O′D∥AC28．解：∵折叠长方形ABCD的一边AD，点D落在BC边的D′处，∴AD=AD′，设AD=xcm，则BD′=（x﹣4）cm，在Rt△ABD′中，AD′2=AB2+D′B2，即x2=82+（x﹣4）2，解得x=10，即AD的长为：10cm29．解：在△ABC中，∠BAC=140°，∴∠B+∠C=180°﹣140°=40°，根据翻折的性质，∠BAD=∠B，∠CAE=∠C，∴∠BAD+∠CAE=∠B+∠C=40°，∴∠DAE=∠BAC﹣∠DAC﹣∠CAE=140°﹣40°=100°30．解：根据轴对称的性质得：OE=EM，OF=FN△OEF的=OE+OF+EF=ME+EF+FN=MN=5cm∴△OEF的周长为5cm．。

八年级数学轴对称画图题专题难点训练学校:___________姓名：___________班级：___________考号：___________一、解答题1．如图，点P是线段AB上的一点，请在图中完成下列操作．（1）过点P画BC的垂线，垂足为H；（2）过点P画AB的垂线，交BC于Q；（3）线段的长度是点P到直线BC的距离．2．作图题:（1）过点A画高AD；（2）过点B画中线BE；（3）过点C画角平分线CF．3．在下面的方格纸中，（1）先画△A1B1C1，使它与△ABC关于直线l1对称；再画△A2B2C2，使它与△A1B1C1关于直线l2对称；（2）若△ABC向右平移2格，则△A2B2C2向平移格．4．如图，在正方形网格上有一个△DEF．（1）画出△DEF关于直线HG的轴对称图形（不写画法）；（2）画EF边上的高（不写画法）；（3）若网格上的最小正方形边长为1，则△DEF的面积为．5．如图，在每个小正方形的边长均为1 个单位长度的方格纸中，有线段AB 和直线MN，点A、B、M、N 均在小正方形的顶点上，在方格纸中画四边形ABCD（四边形的各顶点均在小正方形的顶点上），使四边形ABCD 是以直线MN 为对称轴的轴对称图形，点A 的对称点为点D，点B 的对称点为点C．6．已知：如图，已知△ABC(1)点A关于x轴对称的点A1的坐标是，点A关于y轴对称的点A2的坐标是；(2)画出与△ABC关于x轴对称的△A1B1C1；(3)画出与△ABC关于y轴对称的△A2B2C2．7．如图所示的点A、B、C、D、E．（1）点和点关于x轴对称；（2）点和点关于y轴对称；（3）点A和点D关于直线l成轴对称，请画出直线l．（要求用尺规作图，保留作图痕迹，不必写作法和证明过程）8．如图，根据要求回答下列问题：（1）点A关于y轴对称点A’的坐标是；点B关于y轴对称点B’的坐标是；（2）作出△ABC关于y轴对称的图形△A’B’C’（不要求写作法）（3）求△ABC的面积是9．如图，根据要求回答下列问题：（1）点A关于y轴对称点A′的坐标是；点B关于y轴对称点B′的坐标是（2）作出△ABC关于y轴对称的图形△A′B′C′（不要求写作法）（3）求△ABC的面积．10．如图，利用关于坐标轴对称的点的坐标特点，分别作出△ABC关于x轴和y轴对称的图形．11．如图，（1）在网格中画出ABC 关于y 轴对称的111A B C △；（2）写出ABC 关于x 轴对称的222A B C △的各顶点坐标2A （ ）2B （）2C （ ）参考答案1．（1）详见解析；（2）详见解析；（3）PH．【解析】【分析】利用尺规作出过一点作已知直线的垂线即可解决问题.【详解】解：（1）过点P画BC的垂线，垂足为H，如图所示；（2）过点P画AB的垂线，交BC于Q，如图所示；（3）线段PH的长度是点P到直线BC的距离．故答案为PH．【点睛】本题考查作图-基本作图，点到直线的距离等知识，解题的关键是熟练掌握五种基本作图，属于中考常考题型.2．（1）见解析；（2）见解析；（3）见解析．【解析】【分析】（1）从A点向CB的延长线作垂线．垂足为D，线段AD即所求作的高；（2）作AC的垂直平分线找到中点E，连接BE．BE就是所求的中线；（3）作∠ACB的角平分线，与AB交于点F，CF就是所求的角平分线．【详解】解：（1）如图，用圆规以点A为圆心，大于点A与BC的距离长为半径画弧，与直线CB交于点G，H，分别以G、H为圆心，大于GH的一半为半径画弧，两弧的交于点O，连接AO，交CB的延长线于点D，线段AD即所求作的高；（2）如图，分别以A、C为圆心，大于AC的一半为半径画弧，两弧的交于点J、K，连接JK，与AC交于点E，连接BE，BE就是所求的中线；（3）如图，用圆规以点C为圆心，任意长为半径画弧，再以弧与∠ACB两边的交点M，N 为圆心，大于MN的一半为半径画弧，两弧的交点为P，连接CP并延长，与AB交于点F，CF就是所求的角平分线．【点睛】本题考查作图-复杂作图：复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法．解题的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．3．(1)详见解析;(2)10.【解析】【分析】(1)根据平移性质即可画出图形.(2)由图象格子数即可判断.【详解】(1)由题意画图如下:(2)由图上可得出:若△ABC向右平移2格，则△A2B2C2向左平移10格.【点睛】本题考查平移和对称,关键在于熟练掌握定义.4．（1）详见解析；（2）详见解析；（3）3【解析】【分析】（1）根据网格结构找出点D、E、F关于直线HG的对称点D′、E′、F′的位置，然后顺次连接即可；（2）根据网格结构以及EF的位置，过点D作小正方形的对角线，与FE的延长线相交于H，DH即为所求作的高线；（3）DE为底边，点F到DE的距离为高，根据三角形的面积公式列式进行计算即可得解．【详解】解：（1）如图所示，△D′E′F′即为所求作的△DEF关于直线HG的轴对称图形；（2）如图所示，DH为EF边上的高线；（3）△DEF的面积＝12×3×2＝3．故答案为：3．【点睛】本题考查轴对称作图，熟记相关概念是解题关键.5．图详见解析【解析】【分析】过点A作垂线使AO=DO，过点B作垂线使BP=CP找到点D和点C即可.【详解】如图过点A作垂线使AO=DO，过点B作垂线使BP=CP，依次连接ABCD即可.【点睛】本题考查了图形的对称，解题关键在于对称图形的对应点的连线垂直于对称轴，且对应点距离对称轴的距离相等.6．(1) (－4，－2)，(4，2)； (2)图形见解析(3)图形见解析【解析】试题分析：（1）分别利用关于x轴以及y轴对称点的性质得出对应点坐标即可；（2）直接利用关于x轴对称点的性质得出对应点坐标即可；（3）直接利用关于y轴对称点的性质得出对应点坐标即可．试题解析：(1) (－4，－2)，(4，2)；(2)如图所示：△A1B1C1，即为所求；(3)如图所示：△A2B2C2，即为所求．7．（1）A，E；（2）B，C；（3）详解见图．【解析】【分析】（1）直接利用关于x轴对称点的性质得出答案；（2）直接利用关于y轴对称点的性质得出答案；（3）直接利用线段垂直平分线的作法分析得出答案．【详解】解：（1）点A和点E关于x轴对称；故答案为A，E；（2）点B和点C关于y轴对称；故答案为B，C；（3）如图所示：直线l即为所求．【点睛】此题主要考查了轴对称变换以及线段垂直平分线的作法，正确得出对应点位置是解题关键．8．（1）（3，2），（4，-3）；（2）见解析；（3）13 2【解析】【分析】（1）根据关于y轴对称的点的坐标特点即可得出结论；（2）在坐标系内描出A′，B′，C′三点，再顺次连接即可；（3）利用矩形的面积减去三个顶点上三角形的面积即可．【详解】（1）根据关于y轴对称的点的坐标特点：纵坐标不变，横坐标为相反数，∵A（-3，2），B（-4，-3），∴A′（3，2），B′（4，-3）．故答案为：（3，2），（4，-3）；（2）如图所示；（3）ABC111 35512323 222S=⨯-⨯⨯-⨯⨯-⨯⨯513153322=---=．【点睛】本题考查的是作图-轴对称变换，熟知关于y轴对称的点的坐标特点是解答此题的关键．9．（1）（3，2），（4，﹣3）；（2）图形见解析（3）13 2【解析】试题分析：（1）对照图形可知点A、B的坐标分别：（-3，2）、（-4，-3），由此写出点A′、B′的坐标即可；（2）分别作出点A、B、C关于y轴的对称点A′、B′、C′，再顺次连接这三点即可得到所求三角形；（3）如图，由S△ABC=S矩形DBEF-S△ADB-S△BEC-S△AFC，计算出△ABC的面积即可.试题解析：（1）由图可知：点A、B的坐标分别：（-3，2）、（-4，-3），∴点A、B关于y轴的对称点A′和B′的坐标分别为：（3，2），（4，﹣3）；（2）如下图所示；△A′B′C′为所求的图形；（3）如图：S △ABC =S 矩形DBEF -S △ADB -S △BEC -S △AFC =11135512323222⨯-⨯⨯-⨯⨯-⨯⨯ =515332--- =132． 10．见解析【解析】【分析】根据题意，分别找出三角形各顶点与y 轴、x 轴的对应点，再连接即可.【详解】关于y 轴对称：△A’B’C’为所求；关于x 轴对称：△A’’B’’C’’为所求；11．（1）见解析；（2）32--，；4,3-；1,1-；【解析】【分析】（1）在网格中画出△ABC 关于y 轴对称的△A 1B 1C 1即可；（2）写出△ABC 关于x 轴对称的△A 2B 2C 2的各顶点坐标即可；【详解】解：（1）如图△A 1B 1C 1即为所求作的图形；∴111A B C 即为所求；（2）∵A （-3，2），B （-4，-3），C （-1，-1），∴△ABC 关于x 轴对称的△A 2B 2C 2的各顶点坐标为：A 2（-3，-2），B 2（-4，3），C 2（-1，1）．故答案为：-3，-2；-4，3；-1，1；【点睛】本题考查了轴对称变换、坐标与图形、以及画轴对称图形，解决本题的关键是掌握轴对称性质．。

轴对称作图及应⽤（讲义）（含答案）轴对称作图及应⽤（讲义）课前预习1. 作⼀条线段等于已知线段．已知：如图，线段a ．求作：线段AB ，使AB =a ．作法：（1）作射线AP ；（2）以_________为圆⼼，_______为半径作弧，交射线AP 于点B ．___________即为所求．2. 作⼀个⾓等于已知⾓．已知：如图，∠AOB ．求作：∠A′O′B′，使∠A′O′B′=∠AOB ．OAB作法：（1）作射线O′A′；（2）以________为圆⼼，_______为半径作弧，交OA于点C ，交OB 于点D ；（3）以____为圆⼼，____为半径作弧，交O′A′于点C ′；（4）____________，__________作弧，交前弧于点D ′；（5）过点D ′作射线O′B′．∠A′O′B′_____________．证明：如图，连接________，________．在___________和___________中，______________________________________________________??（已作）（已作）（已作）∴____________________（）∴____________________a知识点睛1.五种基本作图：①作⼀条线段等于已知线段；②作⼀个⾓等于已知⾓；③作已知⾓的⾓平分线；④作已知线段的垂直平分线；⑤过平⾯内⼀点，作已知直线的垂线．精讲精练1.作已知线段的垂直平分线．已知：线段MN．求作：直线AB，使AB垂直平分MN．N作法：（1）分别以_______，______为圆⼼，___________为半径作弧，两弧相交于点A和点B；（2）_______________________________________．_______________________________________．2.（1）过直线上⼀点，作已知直线的垂线．已知：A为直线MN上⼀点．求作：直线AB，使AB⊥MN．A作法：①________________________________________________________________________________________________；②________________________________________________________________________________________________；③________________________________________________．_________________________________________________．（2）过直线外⼀点，作已知直线的垂线．已知：A为直线MN外⼀点．求作：直线AB，使AB⊥MN．AM N作法：①________________________________________________；②________________________________________________________________________________________________；③________________________________________________________________________________________________；④________________________________________________．_________________________________________________．3.作已知⾓的⾓平分线．已知：如图，∠AOB．求作：射线OP，使∠AOP=∠BOP（即OP平分∠AOB）．AOB作法：（1）________________，__________________作弧，交OA于点M，交OB于点N；（2）分别以______，______为圆⼼，______________为半径作弧，两弧在________________交于点P；（3）_________________________．______________________________．4.作已知⾓的四等分线．已知：如图，∠AOB．求作：射线OP，OQ，OM，使∠AOP=∠POQ=∠QOM=∠MOB（即OP，OQ，OM四等分∠AOB）．AOB5.在以下三个图形中，根据尺规作图的痕迹，能判断射线AD平分∠BAC的是（）A．图2 B．图1与图2C．图1与图3 D．图2与图3A BCD图1AB CD图2图3DCBA6.电信部门要修建⼀座电视信号发射塔，如下图，按照设计要求，发射塔到两个城镇A，B的距离必须相等，到两条⾼速公路m，n的距离也必须相等，发射塔P应修建在什么位置？（不写作法，保留作图痕迹）7. 如图，在Rt △ABC 中，∠B =90°，分别以A ，C 为圆⼼，⼤于12AC 长为半径作弧，两弧相交于点M ，N ，作直线MN ，分别交AC ，BC 于点D ，E ，连接AE ，则：（1）∠ADE =_________．（2）AE _______EC ；（填“=”“＞”或“＜”）（3）当AB =3，BC =4时，△ABE 的周长为______．MNED CBAA BCD NM第7题图第8题图8. 如图，在△ABC 中，按以下步骤作图：①分别以点B ，C 为圆⼼，以⼤于12BC 长为半径作弧，两弧相交于M ，N 两点；②作直线MN 交AB 于点D ，连接CD ．若CD =AC ，∠B =25°，则∠ACB 的度数为___________．9. 如图，在△ABC 中，∠C =90°，∠CAB =50°．按以下步骤作图：①以点A 为圆⼼，⼩于AC 的长为半径画弧，分别交AB ，AC 于点E ，F ；②分别以点E ，F 为圆⼼，⼤于12EF 的长为半径画弧，两弧相交于点G ；③作射线AG 交BC 边于点D ．则∠ADC 的度数为_________．GC B A10. 如图，已知点D ，E 分别在∠CAB 的边AB ，AC 上，观察图中作图痕迹，若PD =6，则PE 的最⼩值是（） A ．2B ．3C ．6D ．12EDC BAP11. 如图，在四边形ABCD 中，AD ∥BC ，AD =BC ，AB =CD ，已知CD =8，BC =10，按以下步骤作图：①以点C 为圆⼼，适当长度为半径作弧，分别交BC ，CD 于M ，N 两点；②分别以点M ，N 为圆⼼，以⼤于12MN 的长为半径画弧，两弧在四边形ABCD 的内部交于点P ；③连接CP 并延长交AD 于点E ，交BA 的延长线于点F ，则AE 的长为（） A ．2B ．3C ．4D ．5PF EDC BAMN12. 如图，在四边形ABCD 中，AD ∥BC ，已知∠B =60°，AB =4．以点A 为圆⼼，任意长为半径画弧分别交边AB ，AD 于点M ，N ，再分别以点M ，N 为圆⼼，以⼤于12MN 的长为半径画弧，两弧相交于四边形ABCD 内⼀点P ，连接AP 并延长交BC 边于点E ，连接DE ．当BE =2EC 时，BC 的长为_________．P13.如图，在△ABC中，以点A为圆⼼，AC的长为半径作弧，与BC交于点E，分别以点E，C为圆⼼，⼤于12EC的长为半径作弧，两弧相交于点P，作射线AP交BC于点D．若∠B=45°，∠C=2∠CAD，则∠BAC的度数为（）A．80°B．75°C．65°D．30°E DCBAPCB Al1l21第13题图第14题图14.如图，直线l1∥l2，点A在直线l1上，以点A为圆⼼，适当长度为半径画弧，分别交直线l1，l2于B，C两点，连接AC，BC．若∠ABC=70°，则∠1的⼤⼩为（）A．20°B．35°C．40°D．70°15.已知：如图，线段AB的端点A在直线l上（AB与l不垂直），请在直线l上另找⼀点C，使△ABC是等腰三⾓形．这样的点能找⼏个？请你找出所有符合条件的点．16.已知：如图，线段AB的端点A在直线l上，AB与l的夹⾓为60°，请在直线l上另找⼀点C，使△ABC是等腰三⾓形．这样的点能找⼏个？请你找出所有符合条件的点．【参考答案】 ? 课前预习1. 点Aa 长线段AB 图略2. 作法：（1）作射线O′A′；（2）以点O 为圆⼼，任意长为半径作弧，交OA于点C ，交OB 于点D ；（3）以点O′为圆⼼，OC 长为半径作弧，交O′A′于点C ′；（4）以点C ′为圆⼼，CD 长为半径作弧，交前弧于点D ′；（5）过点D ′作射线O′B′．∠A′O′B′即为所求．证明：如图，连接CD ，C ′D ′．在COD △和C O D '''△中OC O COD O D CD C D ''=??''=??''=?（已作）（已作）（已作）SSS COD C O D '''∴△≌△（） ?∴∠A′O′B′=∠AOB精讲精练 1. 图略（1）点M ，点N ，⼤于12MN 长（2）作直线AB 直线AB 即为所求 2. （1）图略①以点A 为圆⼼，任意长为半径作弧，交直线MN 于C ，D 两点；②分别以点C ，点D 为圆⼼，⼤于12CD 长为半径作弧，两弧交MN 上⽅于⼀点B ；③作直线AB ．直线AB 即为所求．（2）图略①在MN 下⽅任取⼀点P ；②以点A 为圆⼼，AP 长为半径作弧，交MN 于C ，D 两点；③分别以点C ，点D为圆⼼，以⼤于12CD长为半径作弧，两弧交MN下⽅于⼀点B；④作直线AB．直线AB即为所求．3.（1）以点O为圆⼼；任意长为半径；（2）点M；点N；⼤于12MN长；AOB内部；（3）作射线OP；射线OP即为所求．4.略5. C6.略7.（1）90°；（2）=；（3）78.105°9.65°10.C11.A12.613.B14.C15.略16.略。

机器人两朵鲜花第十二讲 设计轴对称图案学习目标：１、能利用轴对称设计简单的图案。

２、经历“操作——猜想——验证”的实践过程，积累数学活动的经验； 3、欣赏生活中的轴对称图案，感受数学丰富的文化价值；重点难点:准确设计的轴对称图案合作探究概念探究：1、分别在下列图形的方格涂上颜色色，使整个图形是成轴对称图形，并与同学交流；2、上台展示你的杰作！3、数学实验：实验一：把一长方形纸片对折两次，画出一个图案并剪去它，把纸展开，与同学交流，教师收集，作为班级厨窗展览材料。

实验二：①制作如图所示的4张正方形纸片； ②将这4张正方形拼合在一起， 就能得到不同的图案，请你试一试还能拼出其它图案吗？优秀作品展示，全班交流，并给作品起名字，注意具有象征意义。

4、操作演示：作△ABC 关于直线l 的对称△A ’B ’C ’例题分析例1、以给定的两个圆、两个三角形、两条平行线为构件，请你尽可能多地构思出独特且有意义的轴对称图形，并写出一两句贴切、灰谐的解说词。

图中就是符合要求的两个图形。

与同学比一比，谁构思的图形多而漂亮。

l例2、某居民小区搞绿化，要在一块长方形空地上建造花坛，现征集设计方案，要求设计的图形由圆与正方形组成（圆与正方形的个数不限），并且使整个长方形场地成轴对称图形，请在下图所示的长方形中画出你设计的方案。

（至少三种）例3、请你应用轴对称的知识画出图中的三个图形，并涂上彩色，与同学比一比，看谁画得正确、漂亮。

例4、在下面的网格内，给出了一个图形和一条直线，试画出已知图形关于直线的轴对称图形。

例5、现有9个相同的小正三角形拼成的大正三角形，将其部分涂黑．如图（1），（2）所示．观察图（1），图（2）中涂黑部分构成的图案．它们具有如下特征：①都是轴对称图形；②涂黑部分都是三个小正三角形．请在图（3），图（4）内分别设计一个新图案，使图案具有上述两个特征．例6、已知图中A，B分别表示正方形网格上的两个轴对称图形（阴影部分），其面积分别记为S1，S2（网格中最小的正方形的面积为一个单位面积），请你观察并回答问题．（1）求s1和s2的值；（2）请你在图C中的网格上画一个面积为8个平方单位的轴对称图形．例7、生活中因为有美丽的图案，才显得丰富多彩，以下是来自现实生活中的三个商标（图1、2、3）（1）以上三个图中轴对称图形有中心对称图形有（2）请在图4中画出是轴对称图形但不是中心对称图形的新图案；在图5中画出是轴对称图形又是中心对称图形的新图案课堂练习达标训练1、聪明的你试试看吧！（1）分析图①，②，④中阴影部分的分布规律，按此规律在图③中画出其中的阴影部分．（2）在下列的图形上补一个小正方形，使它成为一个轴对称图形．2、作图题．（1）观察如图方格子内的两个图形是否成轴对称？若是，请画出它们的对称轴；若不是，请说明理由．（2）请用1个等腰三角形、2个长方形、3个圆形，设计一个轴对称图形，并用简洁的文字说明你的创意．（只留痕迹，不写作法）3、为创建绿色校园，学校决定在一块正方形的空地上种植花草，现向学生征集设计图案．图案要求只能用圆弧在正方形内加以设计，使正方形和所画的图弧构成的图案，是轴对称图形．种植花草部分用阴影表示．请你在图③、图④、图⑤中画出三种不同的设计图案．提示：在两个图案中，只有半径变化而圆心不变的图案属于同一种，例如：图①、图②只能算一种．4、如图是小丽用若干个大小相同的棋子摆成的形如英文大写字母“T”的图形，它是轴对称图形．在以下的方格中请你用若干个棋子重新摆出两个形如英文大写字母的轴对称图形．（用○代表棋子）5、动手操作（1）图1、图2是两张形状、大小完全相同的方格纸，方格纸中的每个小正方形的边长均为1．点A和点B在小正方形的顶点上．①在图1中画出△ABC（点C在小正方形的顶点上），使△ABC为直角三角形（画一个即可）；②在图2中画出△ABD（点D在小正方形的顶点上），使△ABD为等腰三角形（画一个即可）；（2）如图3，画出△ABC关于直线l的对称图形．（3）如图4，A、B、C三点都在方格纸的格点位置上，请你再找一个格点D，使图中的4点组成一个轴对称图形．（画出所有符合条件的点）能力提升1、①在图（1）的方格纸上，将图形沿点划线翻折，画出翻折后的图形．在图（2）的方格纸上，将图形先向右平移3格，再向下平移4格，画出平移后的图形；②在如图所示的方格纸中，经过线段AB外一点C，不用量角器与三角尺，仅用直尺，画线段AB的垂线和平行线．2、如图，DEFG为矩形的台球桌面，现有球A、B位置如图，按下列要求，画出击打后球的线路．（1）击打球A，使它碰撞台边DG后再击中球B；（2）击打球A，使它碰撞台边DG，再碰撞台边DE后击中球B；（3）击打球A，使它碰撞台边GF，再碰撞台边DE后击中球B；（4）击打球A，使它碰撞台边GF，再碰撞台边DG，然后再碰撞台边DE后击中球B．3、生活中，有人喜欢把传送的便条折成“”形状，折叠过程按图①、②、③、④的顺序进行（其中阴影部分表示纸条的反面）：如果由信纸折成的长方形纸条（图①）长为26厘米，分别回答下列问题：（1）如果长方形纸条的宽为2厘米，并且开始折叠时起点M与点A的距离为3厘米，那么在图②中，BE= 厘米；在图④中，BM= 厘米．（2）如果长方形纸条的宽为x厘米，现不但要折成图④的形状，而且为了美观，希望纸条两端超出点P的长度相等，即最终图形是轴对称图形，试求在开始折叠时起点M与点A的距离（结果用x表示）．课外练习1、观察图中的①～④中阴影部分构成的图案．（1）请写出这四个图案都具有的两个共同特征；（2）借助图中之⑤、⑥的网格，请你设计另外二个新的图案，使该图案同时具有你在解答（1）中所写出的两个共同特征．2、用若干根火柴棒可以摆出一些优美的图案．如：下图是用火柴棒摆出的一个图案，此图案表示的含义可以是：天平（或公正）．请你用5根或5根以上火柴棒摆成一个轴对称图案，并说明你画出的图案的含义．3、作图题（1）AC、AB是两条笔直的交叉公路，M、N是两个实习点的同学参加劳动，现欲建一个茶水供应站，使得此茶水供应站到公路两边的距离相等，且离M、N两个实习点的距离也相等，试问：此茶水供应站应建在何处？（2）如图是由25个小正方形组成的正方形网格图，现已将其中的两个涂黑．请你分别在右图（1）、（2）中再涂黑三个空白的小正方形，使得涂黑部分成轴对称图形．（要求图（1）、图（2）的对称轴要有区别）4、现有如图①的瓷砖若干块．（l）用两块这样的瓷砖拼成一个长方形，使拼成的图案呈轴对称图形，请在图②的两个长方形中各画出一种拼法（要求两种拼法不同，所画图案中的阴影部分用斜线表示）；（2）用四块如图①的瓷砖拼成一个正方形，使拼成的图案成轴对称图形，请你在图③的三个正方形中各画出一种拼法，要求同（1）；（3）在第（1）题中，请你计算用如图①的瓷砖拼成的所有长方形中，是轴对称图形的成功率是多少？答案能力提升1、2、解：点A的击打路线分别如图所示：3、。

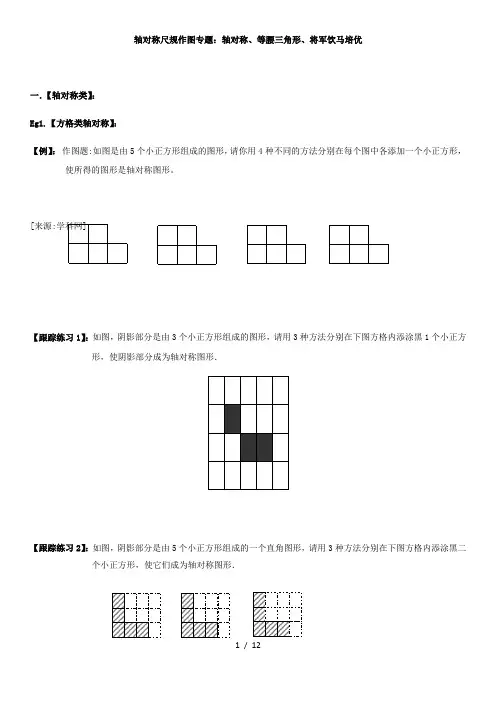
轴对称尺规作图专题：轴对称、等腰三角形、将军饮马培优一．【轴对称类】： Eg1.【方格类轴对称】：【例】： 作图题:如图是由5个小正方形组成的图形，请你用4种不同的方法分别在每个图中各添加一个小正方形，使所得的图形是轴对称图形。

[来源:学科网]【跟踪练习1】：如图，阴影部分是由3个小正方形组成的图形，请用3种方法分别在下图方格内添涂黑1个小正方形，使阴影部分成为轴对称图形．【跟踪练习2】：如图，阴影部分是由5个小正方形组成的一个直角图形，请用3种方法分别在下图方格内添涂黑二个小正方形，使它们成为轴对称图形．【跟踪练习3】：如图是由16个小正方形组成的正方形网格图，现已将其中的两个涂黑．请你用三种不同的方法分别在下图中再涂黑三个空白的小正方形，使它成为轴对称图形．Eg2.【格点类轴对称】：【例1】：在3×3的正方形网格图中，有格点三角形ABC 和格点三角形DEF ，且ABC ∆和DEF ∆ 关于某条直线成轴对称，请在如图①~⑥所示的网格中画出六个这样的DEF ∆.(每种方案均不相同)【跟踪练习】：请在下列三个2×2的方格中，各画出一个三角形，要求所画三角形与图中三角形成轴对称，且所画的三角形顶点与方格中的小正方形顶点重合，并将所画三角形涂上阴影．（注：所画的三个图形不能重复）EABC D【例2】：如图，在所给网格图（每小格均为边长是1的正方形）中完成下列各题：(1)画出格点△ABC （顶点均在格点上）关于直线DE 对称的△A 1B 1C 1 ； (2)在直线DE 上画出点Q ，使最小．【跟踪练习1】：如图，在正方形网格上的一个△ABC ． ⑴ 作△ABC 关于直线MN 的对称图形(不写作法)；⑵ 以P 为一个顶点作与△ABC 全等的三角形（规定点P 与点B 对应，另两顶点都在图中网格交点处)，则可作出____________个三角形与△ABC 全等． (3) 在直线MN 上找一点Q ，使QB+QC 的长最短.【跟踪练习2】：.如图,点A,B,C 都在方格纸的格点上,请你再找一个格点D,使点A,B,C,D组成一个轴对称图形．这QC QA样的点D最多能找到个．【跟踪练习2】：. 如图，在正方形网格中，每个小正方形的边长为1个单位长度.线段AD的两个端点都在格点上，点B是线段AD上的格点，且BD=1，直线l在格线上.(1)在直线l的左侧找一格点C,使得△ABC是等腰三角形(AC<AB)，画出△ABC.(2)将△ABC沿直线l翻折得到△A′B′C′.试画出△A′B′C′.(3)画出点P,使得点P到点D、A′的距离相等,且到边AB、AA′的距离相等.【跟踪练习3】：方格纸中每个小方格都是边长为1的正方形，我们把以格点连线为边的多边形称为“格点多边形”．（1）在图1中画出一个以A、B、C、D为顶点的格点四边形，使其为轴对称图形；（2）在图2中画一个格点正方形，使其面积等于20；（3）直接写出图3中△FGH的面积是________________．【跟踪练习4】：.在图示的方格纸中，（1）画出△ABC关于MN对称的图形△A1B1C1；（2）说明△A2B2C2是由△A1B1C1经过怎样的平移得到的？（3）在直线MN上找一点P，使得PB+PA最短．（不必说明理由）．★【跟踪练习5】：在如图所示的网格中，线段AB和直线l如图所示：（1）借助图中的网格，在图1中作锐角．．△ABC，满足以下要求：①C为格点（网格线交点）；②AB=AC．（2）在（1）的基础上，请只用直尺（不含刻度）在图（1）中找一点P，使得P到AB、AC的距离相等，且PA ＝PB．（友情提醒：请别忘了标注字母！）（3）在图2中的直线l上找一点Q，使得△QAB的周长最小，并求出周长的最小值是．【跟踪练习6】：如图,在每个小正方形的边长均为1个单位长度的方格纸中,有线段AB 和直线MN,点A,B,M,N 均在小正方形的顶点上.(1).在方格纸中画四边形ABCD(四边形的各顶点均在小正方形的顶点上), 使四边形ABCD 是以直线MN 为对称轴的轴对称图形,点A 的对称点为点D, 点B 的对称点为点C;(2).请直接写出四边形ABCD 的周长和面积.Eg3.【等腰三角形类】：【例】：如图，直线l 1、l 2相交于点A ，点B 是直线外一点，在直线l 1、l 2上找一点C ，使△ABC 为一个等腰三角形．满足条件的点C 有（ ） A ．2个 B ．4个C ．6个D ．8个（图1）B Al（图2）B Al⊥，点P是AB上一点，在射线AM与BN上分别作点C、【跟踪练习】：如图，射线AM与BN，MA AB⊥，NB AB点D满足：CPD△为等腰直角三角形，这样的等腰直角三角形可以画（）．A．1个B．2个C．3个D．4个【例】：图l、图2是两张形状、大小完全相同的方格纸，方格纸中的每个小正方形的边长均为1．A和点B在小正方形的顶点上．(1)在图1中画出△ABC(点C在小正方形的顶点上)，使△ABC为直角三角形(画一个即可)；(2)在图2中画出△ABD(点D在小正方形的顶点上)，使△ABD为等腰三角形(画一个即可)；【跟踪练习】：如图A、B在方格纸的格点位置上．若要再找一个格点C，使它们所构成的三角形为轴对称图形，则这样的格点C在图中共有（）A．4个B．6个C．8个D．10个l 2BAl 1Eg4.【垂直平分线与角平分线类】：【例】：“西气东输”是造福子孙后代的创世工程，现有两条高速公路l 1、l 2和两个城镇A 、B （如图），准备建一个燃气控制中心站P ，使中心站到两条公路距离相等，并且到两个城镇等距离，请你画出中心站的位置。

第五章轴对称的性质与作图本章进步目标★★★★★☆Level 5通过对本节课的学习，你能够：1.对轴对称的性质与判定达到【高级理解】级别；2.对垂直平分线与角平分线的相关概念达到【初级运用】级别；3.对路径最短问题达到【高级理解】级别。

VISIBLE PROGRESS SYSTEM进步可视化教学体系据说，古希腊有一位聪明过人的学者，名叫海伦。

有一天，一位将军向他请教了一个问题：从A地出发到河边饮马，然后再去B地，走什么样的路线最短？如何确定饮马的地点？提起路线最短的问题，大家知道，连结两点之间的所有线中，最短的是线段。

这个题中马走的是一条折线。

这该怎么办呢？海伦的方法是这样的：取A关于河岸的对称点A'，连结A'B，与河岸线相交于C，则C点就是饮马的地方。

将军只要从A出发，沿直线走到C，饮马之后，再由C沿直线走到B，所走的路程就是最短的。

如果将军在河边的另外任一点C'饮马，所走的路程就是AC'+C'B，但是，AC'+C'B=A'C'+C'B>A'B=A'C+CB=AC+CB．可见，在C点外任何一点C'饮马，所走的路程都要远一些．这里有几点需要说明：(1)由作法可知，河流l相当于线段AA'的中垂线，所以AD=A'D。

(2)由上一条可知，将军走的路程就是AC+BC，就等于A'C+BC，而两点确定一线，所以C点为最优。

年轻朋友们喜欢打台球，实际上打台球无时无刻都需要应用海伦的妙法。

下面我们看一个有关打台球的实例。

若在矩形的球台上，有两个球在M和N的位置上。

假如从M打出球，先触及AB边E点，弹出后又触到CB边F点，从CB边再反射出来。

问用怎样的打法，才能使这个球反射后正好撞上在N点放置的球？具体做法是：先作M关于AB的对称点M’，再作N关于BC的对称点N’，那么M’N’和BC的交点为E，F；E、F就是球和各边的撞击点。

轴对称尺规作图专题：轴对称、等腰三角形、将军饮马培优一．【轴对称类】：Eg1.【方格类轴对称】：【例】：作图题:如图是由5个小正方形组成的图形，请你用4种不同的方法分别在每个图中各添加一个小正方形，使所得的图形是轴对称图形。

[来源:学科网]【跟踪练习1】：如图，阴影部分是由3个小正方形组成的图形，请用3种方法分别在下图方格内添涂黑1个小正方形，使阴影部分成为轴对称图形．【跟踪练习2】：如图，阴影部分是由5个小正方形组成的一个直角图形，请用3种方法分别在下图方格内添涂黑二个小正方形，使它们成为轴对称图形．【跟踪练习3】：如图是由16个小正方形组成的正方形网格图，现已将其中的两个涂黑．请你用三种不同的方法分别在下图中再涂黑三个空白的小正方形，使它成为轴对称图形．EABC DEg2.【格点类轴对称】：【例1】：在3×3的正方形网格图中，有格点三角形ABC 和格点三角形DEF ，且ABC ∆和DEF ∆ 关于某条直线成轴对称，请在如图①~⑥所示的网格中画出六个这样的DEF ∆.(每种方案均不相同)【跟踪练习】：请在下列三个2×2的方格中，各画出一个三角形，要求所画三角形与图中三角形成轴对称，且所画的三角形顶点与方格中的小正方形顶点重合，并将所画三角形涂上阴影．（注：所画的三个图形不能重复）【例2】：如图，在所给网格图（每小格均为边长是1的正方形）中完成下列各题：(1)画出格点△ABC （顶点均在格点上）关于直线DE 对称的△A 1B 1C 1 ； (2)在直线DE 上画出点Q ，使最小．【跟踪练习1】：如图，在正方形网格上的一个△ABC ． ⑴ 作△ABC 关于直线MN 的对称图形(不写作法)；⑵ 以P 为一个顶点作与△ABC 全等的三角形（规定点P 与点B 对应，另两顶点都在图中网格交点处)，则可作出____________个三角形与△ABC 全等．QC QA +(3) 在直线MN上找一点Q，使QB+QC的长最短.【跟踪练习2】：.如图,点A,B,C都在方格纸的格点上,请你再找一个格点D,使点A,B,C,D组成一个轴对称图形．这样的点D最多能找到个．【跟踪练习2】：. 如图，在正方形网格中，每个小正方形的边长为1个单位长度.线段AD的两个端点都在格点上，点B是线段AD上的格点，且BD=1，直线l在格线上.(1)在直线l的左侧找一格点C,使得△ABC是等腰三角形(AC<AB)，画出△ABC.(2)将△ABC沿直线l翻折得到△A′B′C′.试画出△A′B′C′.(3)画出点P,使得点P到点D、A′的距离相等,且到边AB、AA′的距离相等.【跟踪练习3】：方格纸中每个小方格都是边长为1的正方形，我们把以格点连线为边的多边形称为“格点多边形”．（1）在图1中画出一个以A、B、C、D为顶点的格点四边形，使其为轴对称图形；（2）在图2中画一个格点正方形，使其面积等于20；（3）直接写出图3中△FGH的面积是________________．【跟踪练习4】：.在图示的方格纸中， （1）画出△ABC 关于MN 对称的图形△A 1B 1C 1；（2）说明△A 2B 2C 2是由△A 1B 1C 1经过怎样的平移得到的？（3）在直线MN 上找一点P ，使得PB+PA 最短．（不必说明理由）．★【跟踪练习5】：在如图所示的网格中，线段AB 和直线l 如图所示：（1）借助图中的网格，在图1中作锐角．．△ABC ，满足以下要求：①C 为格点（网格线交点）；②AB =AC ． （2）在（1）的基础上，请只用直尺（不含刻度）在图（1）中找一点P ，使得P 到AB 、AC 的距离相等，且PA＝PB ．（友情提醒：请别忘了标注字母！）（3）在图2中的直线l 上找一点Q ，使得△QAB 的周长最小，并求出周长的最小值是．（图1）BAl（图2）BAl【跟踪练习6】：如图,在每个小正方形的边长均为1个单位长度的方格纸中,有线段AB和直线MN,点A,B,M,N均在小正方形的顶点上.(1).在方格纸中画四边形ABCD(四边形的各顶点均在小正方形的顶点上),使四边形ABCD是以直线MN为对称轴的轴对称图形,点A的对称点为点D,点B的对称点为点C;(2).请直接写出四边形ABCD的周长和面积.Eg3.【等腰三角形类】：【例】：如图，直线l1、l2相交于点A，点B是直线外一点，在直线l1、l2上找一点C，使△ABC为一个等腰三角形．满足条件的点C有（） A．2个 B．4个C．6个 D．8个⊥，点P是AB上一点，在射线AM与BN上分别作点C、【跟踪练习】：如图，射线AM与BN，MA AB⊥，NB AB点D满足：CPD△为等腰直角三角形，这样的等腰直角三角形可以画（）．A．1个B．2个C．3个D．4个【例】：图l、图2是两张形状、大小完全相同的方格纸，方格纸中的每个小正方形的边长均为1．A和点B在小正方形的顶点上．(1)在图1中画出△ABC(点C在小正方形的顶点上)，使△ABC为直角三角形(画一个即可)；(2)在图2中画出△ABD(点D在小正方形的顶点上)，使△ABD为等腰三角形(画一个即可)；l 2B Al 1【跟踪练习】：如图A 、B 在方格纸的格点位置上．若要再找一个格点C ，使它们所构成的三角形为轴对称图形，则这样的格点C 在图中共有（ ）A ．4个B ．6个C ．8个D ．10个Eg4.【垂直平分线与角平分线类】：【例】：“西气东输”是造福子孙后代的创世工程，现有两条高速公路l 1、l 2和两个城镇A 、B （如图），准备建一个燃气控制中心站P ，使中心站到两条公路距离相等，并且到两个城镇等距离，请你画出中心站的位置。