傅里叶光学简介

傅⾥叶光学讲义傅⾥叶光学实验傅⾥叶光学原理的发明最早可以追溯到1893年阿贝（Abbe ）为了提⾼显微镜的分辨本领所做的努⼒。

他提出⼀种新的相⼲成象的原理，以波动光学衍射和⼲涉的原理来解释显微镜的成像的过程，解决了提⾼成像质量的理论问题。

1906年波特（Porter ）⽤实验验证了阿贝的理论。

1948年全息术提出，1955年光学传递函数作为像质评价兴起，1960年由于激光器的出现使相⼲光学的实验得到重新装备，因此从上世纪四⼗年代起古⽼的光学进⼊了“现代光学”的阶段，⽽现代光学的蓬勃发展阶段是从上世纪六⼗年代起开始。

由于阿贝理论的启发，⼈们开始考虑到光学成像系统与电⼦通讯系统都是⽤来收集、传递或者处理信息的，因此上世纪三⼗年代后期起电⼦信息论的结果被⼤量应⽤于光学系统分析中。

两者⼀个为时间信号，⼀个是空间信号，但都具有线性性和不变性，所以数学上都可以⽤傅⽴叶变换的⽅法。

将光学衍射现象和傅⽴叶变换频谱分析对应起来，进⽽应⽤于光学成像系统的分析中，不仅是以新的概念来理解熟知的物理光学现象，⽽且使近代光学技术得到了许多重⼤的发展，例如泽尼克相衬显微镜，光学匹配滤波器等等，因此形成了现代光学中⼀门技术性很强的分⽀学科—傅⾥叶光学。

实验原理：我们知道⼀个复变函数f(x,y)的傅⽴叶变换为：+-=?=dxdy vy ux 2i y x f y x f v u F )](exp[),()},({),(π ( 1 )F (u,v)叫作f(x,y)的傅⽴叶变换函数或频谱函数。

它⼀般也为复变函数，f(x,y)叫做原函数，也可以通过求 F(u,v)逆傅⽴叶变换得到原函数f(x,y)：+=?=-dudv vy ux 2i v u F v u F y x f 1)](exp[),()},({),(π（2）在光学系统中处理的是平⾯图形，当光波照明图形时从图形反射或透射出来的光波可⽤空间两维复变函数（简称空间函数）来表⽰。

在这些情况下⼀般都可以进⾏傅⾥叶变换或⼴义的傅⾥叶变换。

matlab 傅里叶光学全文共四篇示例，供读者参考第一篇示例：傅里叶光学是一种利用傅里叶变换理论研究光传播和光信息处理的方法。

它将光学现象和傅里叶分析有机地结合在一起，通过对光学系统中光场随时间和空间的变化进行频域分析，揭示了光学系统的特性和行为。

傅里叶光学在光学设计、成像系统、数字图像处理等领域具有重要的应用价值，对于提升光学系统的性能和实现更复杂的光学功能具有重要意义。

傅里叶光学的基本原理是将光场视为波动，利用傅里叶变换将光场表示为频谱分解的形式。

在傅里叶光学中，光场的传播和变换可以用傅里叶变换公式描述，通过傅里叶变换可以将一个任意时间或空间变化的光场分解成一系列频率不同的平面波，这些平面波之间的相位和幅度关系代表了原始光场的性质。

通过傅里叶变换，可以实现光场的频域分析，理解光场的传播规律和特性。

在数字图像处理中，傅里叶变换被广泛应用于图像的频域分析和滤波处理。

通过对图像进行傅里叶变换，可以将图像表示为频域上的频谱分布，通过分析频谱特性可以实现图像的去噪、增强、压缩等处理，提高图像质量和清晰度。

傅里叶变换还可以应用于图像配准、图像拼接、图像分割等图像处理任务，为数字图像处理提供了一种有效的工具和方法。

在实际应用中，matlab是一种常用的工具软件，可以实现傅里叶光学的理论研究和数值计算。

matlab软件提供了丰富的函数库和工具箱，可以用于对光场进行傅里叶变换、光学系统的仿真模拟、图像处理和分析等任务。

通过matlab软件，研究者可以方便地进行傅里叶光学的数值计算和模拟，探索光学系统的特性和行为，实现光学功能的设计和优化。

第二篇示例：傅里叶光学是光学领域中一个重要的分支，它利用傅里叶变换的原理来研究光的传播、衍射、干涉等现象。

在傅里叶光学中，光被视为一种波动现象，能够通过数学方法描述和分析光的传播和相互作用。

让我们来了解一下傅里叶光学的基本概念。

在光学中，光波可以被表示为一个复数函数，具有振幅和相位两个要素。

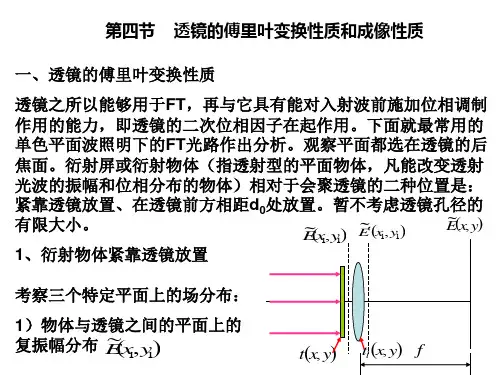
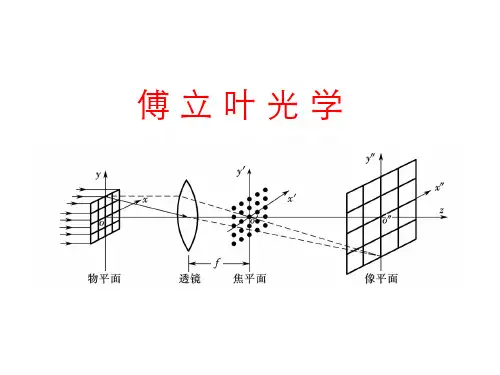
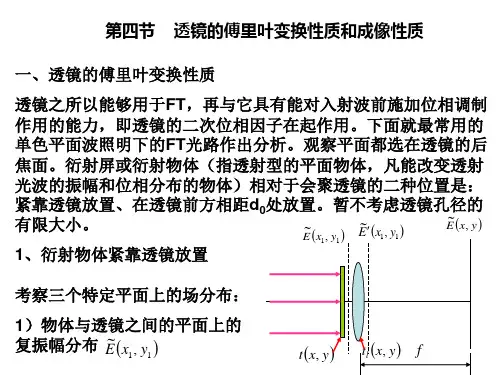
补充读物傅里叶光学和数字图象处理光学与电通讯和电信息理论相互结合，逐渐形成了傅里叶光学。

傅里叶光学的数学基础是傅里叶变换，它的物理基础是光的衍射理论。

一、空间频率和复振幅设一维简谐波以相速度u 沿x 轴正方向传播，)(cos ),(0ϕωξ+−=x k t A t x简谐振动的时间周期性：时间周期T ，时间频率ν，时间角频率ω .简谐波还具有空间周期性？波速u ：(单位时间内振动状态的传播距离称为波速，相速)πλωλνλ2===T u . 空间周期性：空间周期：波长λ (表示振动在一个周期T 内所传播的距离，两个相邻的振动相位相同的点之间距离。

)空间频率：1/λ空间角频率：波数2π/λ若两个单色波沿其传播方向有不同的空间频率，意味着它们有不同的波长。

时间周期性和空间周期性的联系(对单色光)：λ ＝ uT 沿空间任意k 方向传播的单色平面波，复振幅 )(i 00e )(~ϕ−⋅=r k r A E ])cos cos cos ([i 0e ϕγβα−++=z y x k A ,其中α , β 和γ 为传播矢量k 的方位角。

在多数情况下，若不考虑光波随时间的变化，可以只用复振幅表示光波以简化计算。

二、空间频率概念的推广（二维）通常，要处理一个二维的复振幅分布或光强分布，如分析平面上的衍射花样，这时要推广空间频率。

沿k 方向传播的单色平面波，0z z =平面的复振幅分布为 γcos i 000e ),(~z k A y x E =)cos cos (i e βαy x k +对于沿一定方向传播的平面波，γcos i 0e z k ＝常数，则A y x E =),(~0)cos cos (i e βαy x k +x, y 平面上各点复振幅的差别仅来源于不同的(x, y )处有不同的相位差。

x y 平面上的相位分布？k 方向传播的平面波的波面如上图示，0z z =平面与任一波面的交线(虚线)上，各点的位相＝该波面的相位值；交线族 ＝ 等相位线族，其方程为 =+)cos cos (2βαλπy x 常数 故，0z z =平面上复振幅分布的特点：等位相线是一组平行线, 呈周期分布(周期为π2)。

傅里叶光学的应用
傅里叶光学是光学领域的一种重要理论，它被广泛用于光学成像、信号处理、光通信等方面。

在光学成像方面，傅里叶光学应用最为广泛，它可以帮助我们理解复杂的光学图像。

傅里叶光学的应用还包括材料科学、量子光学等领域。

傅里叶光学的一个重要应用是光学相干成像，它利用傅里叶光学的原理，通过波前重构技术，使光束穿过被成像物体时，记录下干涉图像。

然后，通过解析干涉图像，可以重建出物体的三维结构。

这种技术在光学显微成像、医学成像等方面得到了广泛应用。

除此之外，傅里叶光学还可以用于压缩成像。

我们知道，通常成像需要大量的数据才能呈现图片。

但傅里叶光学可以在不损失图像质量的情况下，将图像的数据量大大减少，从而提高成像速度和效率。

这种技术在太空望远镜、医学影像等方面应用广泛。

此外，傅里叶光学在光通信中也有重要应用。

当光信号经过光纤传输时，受到的干扰和失真会导致信号品质下降。

而傅里叶光学可以用于信号重构，对光信号进行滤波、增强和复原等处理，从而提高信号传输的质量和效率。

这种技术在光通信系统中应用广泛。

总之，傅里叶光学的应用广泛，它不仅可以帮助我们实现高效的光学成像，还可以在光通信、材料科学、量子光学等领域发挥重要作用。

傅里叶光学
傅里叶光学的原理是根据傅里叶分析的原理，利用光的波动特性，将一个复杂的光波分解成多个简单的光波，然后利用这些简单的光波来描述复杂的光波的特性。

这种分析方法可以用来研究光的传播，衍射，折射，反射和其他光学相关的现象，可以研究光的空间分布，特性，调制，幅度，相位等特性。

傅里叶光学是一种基于傅里叶变换的光学理论，它用来描述光线的行为，其中光线的行为可以用傅里叶变换的形式表示。

它是由法国物理学家和数学家约瑟夫·傅里叶发现的，他在1822年发表了一篇论文，提出了“傅里叶光学”的概念，并且将其用于描述光线的行为。

傅里叶光学的基本原理是，光线可以用一系列的正弦函数来表示，这些正弦函数的频率和振幅可以用傅里叶变换来表示。

换句话说，傅里叶光学可以用来描述光线如何传播，如何反射，如何折射，以及如何在介质中传播，等等。

傅里叶光学的原理被广泛应用于光学，以及其他科学和工程领域。

它可以用来解释和模拟光线在不同环境中的传播特性，以及光线在介质中的反射、衍射和折射等现象。