傅里叶光学解析
- 格式:ppt
- 大小:8.57 MB
- 文档页数:8


第1篇一、实验目的1. 深入理解傅里叶光学的基本原理和概念。
2. 通过实验验证傅里叶变换在光学系统中的应用。
3. 掌握光学信息处理的基本方法,如空间滤波和图像重建。
4. 理解透镜的成像过程及其与傅里叶变换的关系。
二、实验原理傅里叶光学是利用傅里叶变换来描述和分析光学系统的一种方法。
根据傅里叶变换原理,任何光场都可以分解为一系列不同频率的平面波。
透镜可以将这些平面波聚焦成一个点,从而实现成像。
本实验主要涉及以下原理:1. 傅里叶变换:将空间域中的函数转换为频域中的函数。
2. 光学系统:利用透镜实现傅里叶变换。
3. 空间滤波:在频域中去除不需要的频率成分。
4. 图像重建:根据傅里叶变换的结果恢复原始图像。
三、实验仪器1. 光具座2. 氦氖激光器3. 白色像屏4. 一维、二维光栅5. 傅里叶透镜6. 小透镜四、实验内容1. 测量小透镜的焦距实验步骤:(1)打开氦氖激光器,调整光路使激光束成为平行光。
(2)将小透镜放置在光具座上,调节光屏的位置,观察光斑的会聚情况。
(3)当屏上亮斑达到最小时,即屏处于小透镜的焦点位置,测量出此时屏与小透镜的距离,即为小透镜的焦距。
2. 利用夫琅和费衍射测光栅的光栅常数实验步骤:(1)调整光路,使激光束通过光栅后形成衍射图样。
(2)测量衍射图样的间距,根据dsinθ = kλ 的关系式,计算出光栅常数 d。
3. 傅里叶变换光学系统实验实验步骤:(1)将光栅放置在光具座上,调整光路使激光束通过光栅。
(2)在光栅后放置傅里叶透镜,将光栅的频谱图像投影到屏幕上。
(3)在傅里叶透镜后放置小透镜,将频谱图像聚焦成一个点。
(4)观察频谱图像的变化,分析透镜的成像过程。
4. 空间滤波实验实验步骤:(1)将光栅放置在光具座上,调整光路使激光束通过光栅。
(2)在傅里叶透镜后放置空间滤波器,选择不同的滤波器进行实验。
(3)观察滤波后的频谱图像,分析滤波器对图像的影响。
五、实验结果与分析1. 通过测量小透镜的焦距,验证了透镜的成像原理。

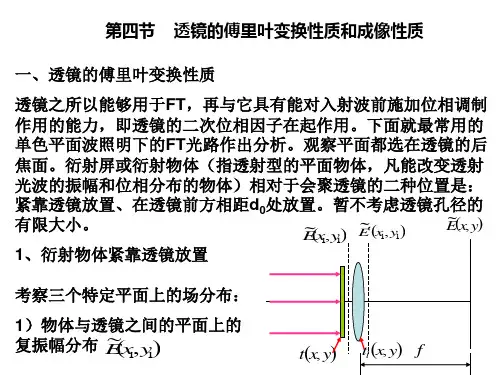

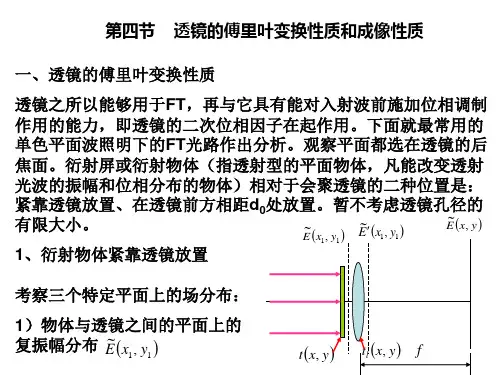
光学成像的傅里叶光学解析光学成像是一种利用光学原理来获取目标物体的图像或信息的技术。
傅里叶光学解析是与光学成像密切相关的一种数学分析方法,它可以帮助我们理解光学成像的原理和性能。
傅里叶光学解析是基于傅里叶变换的数学理论,该理论指出任何波形都可以分解成一系列不同频率的正弦波或余弦波的叠加。
在光学中,傅里叶光学解析将光波分解成不同的频率组成部分,并分析它们对成像的贡献。
在光学成像中,光线从物体表面反射或透过物体后进入成像系统,然后被透镜或其他光学元件聚焦成像。
而傅里叶光学解析则通过对光场的傅里叶变换,计算光场的频谱分布,进而解析出图像的信息。
傅里叶光学解析在光学成像中的应用广泛。
首先,它可以用于评估成像系统的成像性能。
通过分析光波的频谱分布,我们可以了解光学系统在不同频率上的传输特性,从而评估系统的分辨率和失真程度。
这可以帮助我们设计和优化成像系统,以获得更好的图像质量。
其次,傅里叶光学解析可以用于图像复原和重建。
在实际成像过程中,光波会受到各种因素的影响,如散射、衍射、干涉等,并且会产生噪声和畸变。
通过对光场进行傅里叶变换,我们可以在频域上对图像进行修复和重建,减少噪声和畸变的影响,提高图像的质量和清晰度。
此外,傅里叶光学解析还可以用于图像处理和分析。
光学成像获得的图像往往包含大量的信息,通过傅里叶光学解析,我们可以将不同频率的信息分离出来,进一步分析和处理图像。
例如,可以通过滤波的方法去除图像中的某些频率成分,突出图像中的某些特征或结构。
最后,傅里叶光学解析还可以用于其他光学应用,如光学显微镜、光学干涉仪、光学测量等。
通过应用傅里叶光学解析,我们可以获得更多的图像信息,并进一步深入理解和研究光学现象。
综上所述,傅里叶光学解析作为光学成像的数学分析方法,对于理解光学成像的原理和性能非常重要。
它可以帮助我们评估成像系统的性能,修复和重建图像,进行图像处理和分析,以及应用于其他光学领域。
通过深入研究和应用傅里叶光学解析,我们可以进一步推动光学成像技术的发展和创新。


光学经典理论|傅里叶光学基础2018-02-24 17:00今天的光学经典理论为大家带来的是傅里叶光学基础,傅里叶光学是现代光学的一个分支,将电信理论中使用的傅里叶分析方法移植到光学领域而形成的新学科。
光学人们可以看看!在电信理论中,要研究线性网络怎样收集和传输电信号,一般采用线性理论和傅里叶频谱分析方法。
在光学领域里,光学系统是一个线性系统,也可采用线性理论和傅里叶变换理论,研究光怎样在光学系统中的传播。
两者的区别在于,电信理论处理的是电信号,是时间的一维函数,频率是时间频率,只涉及时间的一维函数的傅里叶变换;在光学领域,处理的是光信号,它是空间的三维函数,不同方向传播的光用空间频率来表征,需用空间的三维函数的傅里叶变换。
包含内容60年代发明了激光器,使人们获得了新的相干光源后,傅里叶光学无论在理论和应用领域均得到了迅速发展。
傅里叶光学运用傅里叶频谱分析方法和线性系统理论对广泛的光学现象作了新的诠释。
其主要内容包括标量衍射理论、透镜成像规律以及用频谱分析方法分析光学系统性质等。
推导演示一个光学信息系统和一个电学信息系统有许多相同之处,它们都是收集信息和传递信息,它们都有共同的数学工具──线性系统理论和傅里叶分析。
从信息论角度,关心的是信息在系统中传递过程;同样,对一个光学系统来讲,物和像的关系,也可以根据标量衍射理论由系统中光场的传播来确定,因此光学系统可以看成一个通信信道。
这样,通信理论中已经成熟的线性系统理论可以用来描述大部分光学系统。
当物体用非相干光照射时,在系统像平面上强度分布与物体上强度分布成线性(正比)关系。
而用来描述电学系统的脉冲响应h(t,τ)概念,即系统对一窄脉冲δ(t)(狄喇克δ函数)的响应,也可以用来描述光学系统,即用光学系统对点光源δ(x,y)的响应(点光源的像)h(x,y;ξ,η)来描述系统的性质,两者的区别仅仅在于电学系统的脉冲响应是时间一维函数,光学系统的脉冲函数是空间二维函数,另外两者都具有位移不变性,前者分布不随时间位移而变,后者分布不随空间位移而变(即等晕条件)。



第一章 傅里叶分析第一章内容为傅里叶光学课程的数学基础。
主要介绍了δ函数的定义及其相关性质,由δ函数引申出梳状函数。
介绍了其他一些常用函数:阶跃函数、符号函数、矩形函数、三角形函数、sinc 函数、高斯函数和圆域函数等,主要用于表述振幅透过率或者光强分布等。
重点讲解了以上常用函数的傅里叶变换以及傅里叶变换的主要性质。
另一个重要内容是卷积与相关性,它们在后续的学习中均有十分重要的应用。
δ函数:常用于描述点质量、点电荷、点光源等在某一坐标系中高度集中的物理量。
○1筛选性:()()()0000,,d d ,x x y y x y x y x y δφφ∞--=⎰⎰ ○2比例变换性:()()1,,ax by x y abδδ= ○3与普通函数乘积:()()()()000000,,,,f x y x x y y f x y x x y y δδ--=--梳状函数:常用于对其他函数作等间距抽样。
○1()()n comb x x n δ∞=-∞=-∑ ○2()1n x comb x n δτττ∞=-∞⎛⎫=- ⎪⎝⎭∑ ○3与普通函数乘积:()()()1n x f x comb f n x n τδτττ∞=-∞⎛⎫=- ⎪⎝⎭∑卷积:()()()(),,,,d d f x y h x y f h x y ξηξηξη∞*=--⎰⎰○1展宽:一般卷积的宽度等于被卷积函数宽度之和; ○2平滑化:被卷积函数经卷积运算,其细微结构在一定程度上被消除。
相关:包括自相关与互相关。
互相关是两个信号之间存在多少相似性的量度;自相关是同一函数自变量相差某一大小时,函数值间相关的量度。
对于周期函数(满足狄里赫利条件),可以将其展开为傅里叶级数形式,包括三角傅里叶级数和指数傅里叶级数;它的傅里叶系数是频率的函数,称为频谱函数,是离散的。
对于非周期函数,可以作傅里叶变换,它的频谱函数是连续的。
主要讨论傅里叶变换:空间域 ()()(),,exp 2d d x y x y x y g x y G f f j xf yf f f π∞⎡⎤=+⎣⎦⎰⎰ 频域 ()()(),,exp -2d d x y xy G f f g x y j xf yf x y π∞⎡⎤=+⎣⎦⎰⎰ 卷积定理:()(){}()()()(){}()(),,,,,,,,x y x yx y x yg x y h x y G f f H f f g x y h x y G f f H f f *==*常见傅里叶变换对:见课本p39。
傅里叶光学衍射
傅里叶光学是一种基于傅里叶变换的光学分析方法,用于研究和描述光的传播、传输和干涉等现象。
衍射则是傅里叶光学中的一个重要概念,指的是光波在通过绕射物体或在光学衍射装置中遇到不同障碍物或孔径时发生的偏折、干涉和广泛分布的现象。
当光波通过一个物体或孔径时,由于光的波动性,光波在物体边缘处发生弯曲,并产生干涉、衍射效应。
这导致光波的幅度和相位在空间中发生变化,进而在接收屏幕上形成特定的光强和亮度分布。
衍射现象可以通过傅里叶光学的数学表达进行理解和描述。
根据傅里叶光学的原理,复杂的光波可以被分解成一系列具有不同频率的简单正弦波。
衍射可以被看作是这些不同频率的波在空间中互相干涉和综合的结果。
傅里叶光学提供了描述衍射现象的数学工具和方法,例如使用傅里叶变换分析光的传播和干涉,以及通过傅里叶光学的逆变换来重建或模拟复杂的光场。
衍射现象在许多光学应用中发挥着重要作用,例如在光学衍射实验中观察衍射图样,可用于分析和测量光源、物体的结构和特性。
此外,衍射也被广泛应用于光学显微镜、天文望远镜、激光技术等领域,为光学系统的设计和优化提供
重要参考。