傅里叶光学基础课件

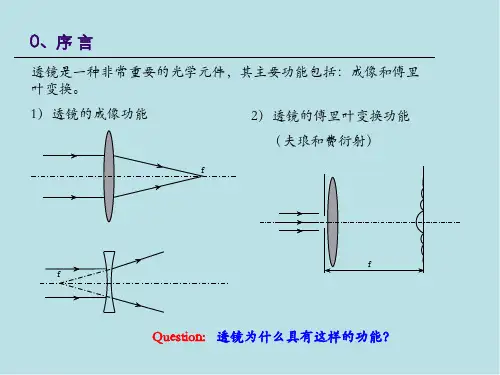
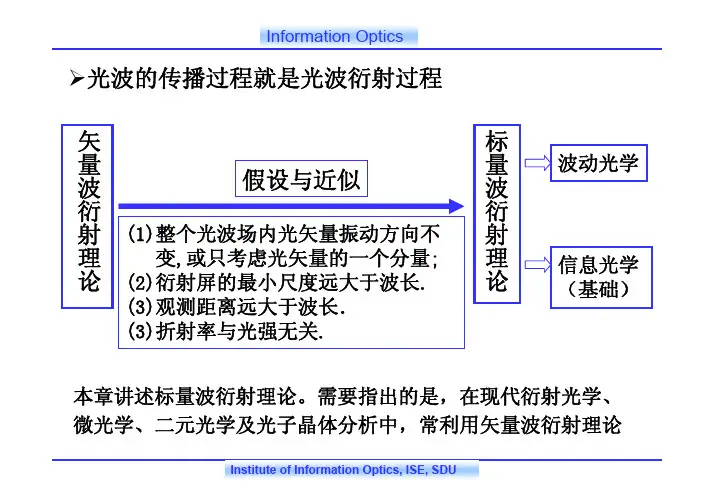
光波的传播过程就是光波衍射过程假设与近似(1)整个光波场内光矢量振动方向不变,或只考虑光矢量的一个分量;(2)衍射屏的最小尺度远大于波长.(3)观测距离远大于波长．光波衍射的线性系统分析基尔霍夫波衍射理论(书2.1惠更斯－菲涅耳原理与基尔霍夫衍射理论一、惠更斯－菲涅耳原理子波(次波)相干叠加0exp()(,)jkr K r θθdU (Q )0)jkr Σ••QrΣnθθS 1S 20exp()1(cos 2jkr r θi是在无限大不透光屏上有一开孔的情况下推导出的. 但可以推广到其它任何复杂的衍射屏。

只是此时，公式中:()()()i P U P t P =入射到衍射屏上的光场的复振幅分布，衍射屏的复振幅透过率。

光波衍射过程是线性系统变换基尔霍夫衍射积分公式为:1e (x )p j krjkr j r 1exp()1(cos 2λ=i 此式是一个叠加积分，满足线性系统的叠加性和均匀性。

因此衍射过程（光波从衍射平面到观察平面的传播过程）可以看作是一个线性系统。

是该线性系统的脉冲响应(点扩散函数可以看作是: 衍射屏上P 点的一个单位脉冲在场产生的复振幅分布。

它描述了衍射系统的特性。

相干光场在自由空间传播的平移不变性2z距z 足够大），且观察范围较0cos 1θ≈(U x 0r Si(x 0这表明，在满足一定条件下，衍射屏上各次波源在场点处所产生的复振幅分布具有相同的分布形式，只是发生了也就是说，具有平移不变性。

可写成卷积形式：21exp jk z zλ⎡+⎣0)(,)y h x x y y −−相干光场在自由空间传播的脉冲响应的近似表达式21exp jk z j zλ⎡⎣220)()1y y z ⎡+−=⎢⎣一、菲涅耳近似(傍轴近似) →菲涅耳衍射在衍射屏和观察范围确定后，当项以后的高次项，不会引起明显的相位误差。

高次项中，起主要作用的是第3项，即当由第20()(28x x zπλ⎡−+⎣201()(8x x λ⎡−+⎣exp()exp jkz jk j z λ⎡=⎢⎣系统的脉冲响应可表示为：菲涅耳衍射的脉冲响应，仍具有平移不变性0002(,)exp exp()exp 2U x y jk jkz x jk j z z λ∞−∞⎡⎢⎣⎡+⎢⎣∫二、夫琅禾费近似（远场近似）→在菲涅耳近似的基础上，如果z 进一步增大，且进一步限定衍射屏透光区域，以至于：2max 2π 可以忽略，忽略该项所引起的相位误差很小22)y y x ⎤−exp())exp jkz x jk j z λ⎛=⎜⎝22exp 2(2y x j x z z πλ⎞+⎡−⎟⎢⎣⎠000)(,;,)y h x y x y dx 则衍射的光场分布为:从上式可以看出：夫琅禾费衍射仍是线性系统，但不是平移不变系统，不再具有平移不变性。

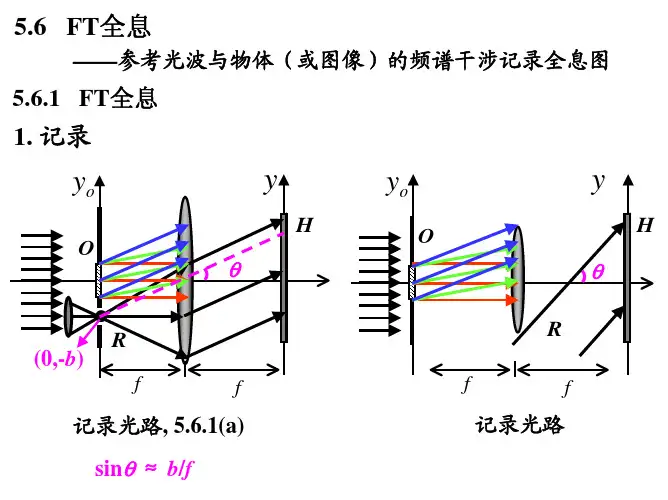
专题：傅里叶光学基础Fundamentals of Fourier Optics§1.1 数学基础知识和傅里叶变换的基本概念§1.2 光波的傅里叶分析§1.3 平面波角谱理论§1.4 透镜的傅里叶变换§1.5 光阿贝成像原理§1.6 光全息术傅里叶光学：研究以光作为载波，实现信息传递、变换、记录和再现的问题。

§1.1 数学基础知识和傅里叶变换的基本概念一、一些常用函数在现代光学中，常用各种非初等函数和特殊函数来描述光场的分布。

常用函数定义图形表示应用阶跃函数1 x0step(x )1step( ) 2 0x x1x0 x 0直边（或刀口）的透过率符号函数1 0xsgn(x) 0 x 01 x 0孔径的一半嵌有相位板的复振幅透过率矩形函数xrect( )ax1 1/ 2a0 else狭缝或矩孔的透过率常用函数定义图形表示应用三角形函数| x|x1 x 1( ) aa0 else光瞳为矩形的非相干成像系统的光学传递函数狭缝或矩孔的sinc函数x sin( x/ a )sinc( )a x/ a 夫琅禾费衍射图样高斯函数2x xGaus( ) expa a 激光器发出的高斯光束x y2 2circ( )r圆域函数圆孔的透过率2 21 x y r0 else二、傅里叶级数的定义一个周期性函数g(x) ，周期为T（频率f = 1/T ），在满足狄里赫利条件（函数在一个周期内只有有限个极值点和第一类不连续点），可以展开为三傅里叶系数角傅里叶级数:ag x a nfx b nfx()cos(2)sin(2)n n2n1在[-T/2, T/2]区间逐项积分：a aT2T2T2T2g x dx dx a nfx dx b nfx dx T()cos(2)sin(2)00(1) nn2 2T2T2T2T2n1因此有：2T2a g(x)dx 02TT将公式(1)两端同乘以cos(2πmfx)，并利用三角函数的正交性：0,for m n0, sin(mx)sin(nx)dx cos(mx)cos(nx)dx,for m n ,sin(mx)cos(nx)dx0,for any m and n for m n for m n逐项积分：aT2T2g(x)cos(2mfx)dx cos(2mfx)dxT2T2= 02= 0T2T2a cos(2nfx)cos(2mfx)dxb sin(2nfx)cos(2mfx)dxn T n T22 n1(m n)T2aa nfx dx Tcos(2)n2n T222T2a g(x)cos(2nfx)dxn TT2系数：2T/2直流分量a g(x)dx0/2TT2T/2余弦分量的幅度a g(x)cos2nfx dxn TT/22T/2正弦分量的幅度b g(x)s in2nfx dxn TT/2用傅里叶级数展开表示矩形周期函数ag x a nfx b nfx ()cos2sin2n n2n1f 周期信号可分解为直流，基波( )和f nf各次谐波( )的线性组合。