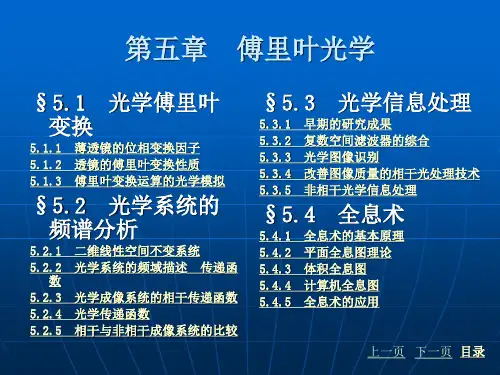
傅里叶光学

第1篇一、实验目的1. 深入理解傅里叶光学的基本原理和概念。

2. 通过实验验证傅里叶变换在光学系统中的应用。

3. 掌握光学信息处理的基本方法，如空间滤波和图像重建。

4. 理解透镜的成像过程及其与傅里叶变换的关系。

二、实验原理傅里叶光学是利用傅里叶变换来描述和分析光学系统的一种方法。

根据傅里叶变换原理，任何光场都可以分解为一系列不同频率的平面波。

透镜可以将这些平面波聚焦成一个点，从而实现成像。

本实验主要涉及以下原理：1. 傅里叶变换：将空间域中的函数转换为频域中的函数。

2. 光学系统：利用透镜实现傅里叶变换。

3. 空间滤波：在频域中去除不需要的频率成分。

4. 图像重建：根据傅里叶变换的结果恢复原始图像。

三、实验仪器1. 光具座2. 氦氖激光器3. 白色像屏4. 一维、二维光栅5. 傅里叶透镜6. 小透镜四、实验内容1. 测量小透镜的焦距实验步骤：（1）打开氦氖激光器，调整光路使激光束成为平行光。

（2）将小透镜放置在光具座上，调节光屏的位置，观察光斑的会聚情况。

（3）当屏上亮斑达到最小时，即屏处于小透镜的焦点位置，测量出此时屏与小透镜的距离，即为小透镜的焦距。

2. 利用夫琅和费衍射测光栅的光栅常数实验步骤：（1）调整光路，使激光束通过光栅后形成衍射图样。

（2）测量衍射图样的间距，根据dsinθ = kλ 的关系式，计算出光栅常数 d。

3. 傅里叶变换光学系统实验实验步骤：（1）将光栅放置在光具座上，调整光路使激光束通过光栅。

（2）在光栅后放置傅里叶透镜，将光栅的频谱图像投影到屏幕上。

（3）在傅里叶透镜后放置小透镜，将频谱图像聚焦成一个点。

（4）观察频谱图像的变化，分析透镜的成像过程。

4. 空间滤波实验实验步骤：（1）将光栅放置在光具座上，调整光路使激光束通过光栅。

（2）在傅里叶透镜后放置空间滤波器，选择不同的滤波器进行实验。

（3）观察滤波后的频谱图像，分析滤波器对图像的影响。

五、实验结果与分析1. 通过测量小透镜的焦距，验证了透镜的成像原理。

第一章光场的表示和Fourier分析1.1 Maxwell方程与标量波1.2 平面波和球面波1.3 二维Fourier变换的定义和物理意义1.4 卷积和相关1.5 Fourier变换的基本性质1.6 可分离变量的Fourier变换1.7 一些常用函数和它们的Fourier变换17空间频率概念的引入f (2j eU )y ,x (U π=/1/1==f f y x λcos =X9112. ( f x , f y )的物理意义方向余弦为(cos α, cos β) 的单色平面波在xoy平面上的复振幅分布是以2π为周期的分布，该复振幅分布可用沿x，y 方向的空间频率( f x , f y ) 来描述3.根据波叠加原理，任何复杂的光场分布可以分解为许多不同方向传播的平面波的叠加，或分解为许多不同空间频率的波的叠加.此式表示一个在xy 平面上沿x方向的空间频率为f x ，沿y方向的空间频率为f y 作周期的复振幅函数，它代表一个传播方向为( cos α＝λf x ，cos β＝λf y )的平面波.)(20),(y f x f j y x eU y x U +=π)cos cos (0),(βαy x jk e U y x U +=四、球面波的复振幅1、定义：点光源发出的单色光波等相位面是球面波1215近轴条件：只考虑xoy 平面上与S 点张角不大的范围.3、近轴条件下球面波的复振幅(1)171.3 Fourier变换的定义和物理意义一、广义变换∫∞∞−=dxx k x f I f ),()()(αα把函数f (x)在x 空间变换成α空间的I f (α)的函数，I f (α) 叫函数f (x) 的以k (α,x) 为核的积分变换.变换Fourier e x k x j −−=−παα2),(拉普拉斯变换−−−x e α梅林变换−−−1αx 阶汉克尔变换n xJ n −−)(α18二、一维Fourier变换1、定义t j eπν2基元函数代表频率为ν的简谐振荡.F (ν)= F {f ( t )}=∫∞∞−−dte tf t j πν2)({}dve v F v F tf vt j π21)()()(∫∞∞−−==F 2、物理意义：1) f (t)可分解为许多基元函数的线性组合;2) F (ν)权重因子.1921四、存在条件(函数g(x,y)存在FT的条件)1、g(x,y)在整个xy平面绝对可积∫∫∞<dxdy y x g |),(|五、广义Fourier变换g (x ,y)＝),(lim y x g n n ∞→G (f x ,f y )＝),(lim y x n n f f G ∞→2、在任一有限区域里，g(x,y) 必须只有有限个间断点和有限个极大和（或）极小点;3、g(x,y)必须没有无限大间断点.23若g(x,y) 为实函数，G( f x , f y ) 是厄米函数，则G (-f x ,-f y ) = ( f x , f y )即振幅|G (-f x ,-f y ) | = |G( f x , f y )|幅角φ(-f x ,-f y ) = -φ( f x , f y )其中( f x , f y )是G( f x , f y )的共轭复数，G ( f x , f y )是中心对称的函数.傅立叶变换并不改变函数的奇偶性,通常该性质称为傅立叶变换的对称性.∗G ∗G24一、卷积（Convolution）1. 定义：αααd x h f x h x f x g )()()()()(−∫=∗=∞∞−展宽：卷积运算的宽度是原来两个函数宽度之和.设f (x) 宽度为b 1, h (x) 的宽度为b 2,则g (x) 的宽度是：b = b 1＋b 2 .1.4 卷积和相关卷积运算的几何解释：先反转h (α)，每平移一个距离x，计算f (α)h (x -α)相乘，∫∞∞−−da a x h a f )()(求面积；再绘成g(x) 随x 变化的图形；积分252627)}()({)}()({)()}()({x h x v b x h x u a x h x bv x au ∗+∗=∗+4)结合性：)()()()()()()()}()({x v x h x u x h x v x u x h x v x u ∗∗=∗∗=∗∗)()()(x u x v x h ∗∗=卷积的次序是无关紧要的.2. 性质：1)平滑性：g (x)的变化率<< f (x)、h (x)的最大变化率；2)对易性：f (x) * h (x)= h (x) * f(x)；3)线性性质：30二、相关（correlation）1. 定义：αααd x h f x h x f x g )()()()()(*−∫==∞∞−★令：x −=αβ得：βββd h x f )()(*∫∞∞−+ηξηξηξd d y x h f y x h y x f y x g ),(),(),(),(),(*−−∫∫=∞∞−＝★ηξηξηξ′′′′∫∫+′+′∞∞−d d h y x f ),(),(*＝与卷积运算的区别：没有反转，只有平移.)(αh )(α−h31相关运算示意图322.性质：1)尖峰化：相关运算是两个信号之间存在相似性的量度.34若f (x) = h (x),则：αααd x f f x f x f x g )()()()()(*−∫==∞∞−★ηξηξηξ∫∫−−=∞∞−d d y x f f y x f y x f ),(),(),(),(*★ηξηξηξ′∫∫′′′+′+′=∞∞−d d f y x f ),(),(*3. 自相关函数：1)定义：3538六、自相关定理七、Fourier积分定理对函数相继进行正FT变换和逆FT，得到原函数.八、FT的FT对函数相继进行FT，所得的函数形式不变，仅将坐标反向.F {g (x,y )☆g (x,y )}=|G (f x , f y )|2F {|G (f x , f y )|2}= g (x,y )☆g (x,y )F –1{F {g (x,y )}}= F {F –1{g (x,y )}}=g (x,y )F {F {g (x,y )}}=g (-x,-y )自相关函数的FT是原函数的功率谱，信号的自相关和功率谱之间存在FT关系.F {g (x,y )☆h (x,y )}= (f x , f y )·H (f x , f y )——互相关定理∗G 两函数的互相关与其互谱密度之间存在FT关系.41结论：在极坐标中可分离变量函数g (r ,θ)=g r (r )g θ(θ)它的频谱在极坐标中也是可分离变量函数，关于φ的函数是exp(j k φ)，关于ρ的函数是G k (ρ) 它为g r (r ) 的k 阶汉克尔变换.=ρ45464748491.7、一些常用函数和它们的FT50。

傅里叶光学
傅里叶光学的原理是根据傅里叶分析的原理，利用光的波动特性，将一个复杂的光波分解成多个简单的光波，然后利用这些简单的光波来描述复杂的光波的特性。

这种分析方法可以用来研究光的传播，衍射，折射，反射和其他光学相关的现象，可以研究光的空间分布，特性，调制，幅度，相位等特性。

傅里叶光学是一种基于傅里叶变换的光学理论，它用来描述光线的行为，其中光线的行为可以用傅里叶变换的形式表示。

它是由法国物理学家和数学家约瑟夫·傅里叶发现的，他在1822年发表了一篇论文，提出了“傅里叶光学”的概念，并且将其用于描述光线的行为。

傅里叶光学的基本原理是，光线可以用一系列的正弦函数来表示，这些正弦函数的频率和振幅可以用傅里叶变换来表示。

换句话说，傅里叶光学可以用来描述光线如何传播，如何反射，如何折射，以及如何在介质中传播，等等。

傅里叶光学的原理被广泛应用于光学，以及其他科学和工程领域。

它可以用来解释和模拟光线在不同环境中的传播特性，以及光线在介质中的反射、衍射和折射等现象。

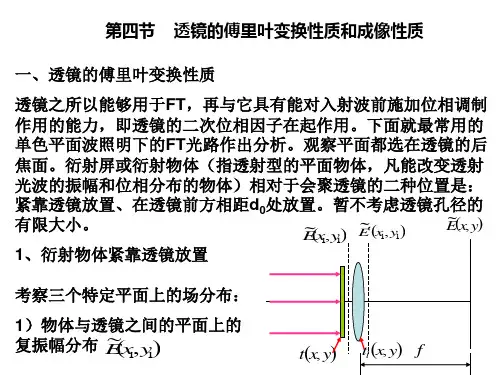
傅里叶变换光学系统
傅里叶变换光学系统是一种基于傅里叶变换原理的光学成像系统。

傅里叶变换可以将一个复杂的光学信号分解成一系列简单的正弦或余弦波，从而实现对信号频率谱的分析。

在光学成像中，傅里叶变换可以用来处理图像，将图像分解成不同的频率成分，从而实现图像增强、滤波、去噪等功能。

傅里叶变换光学系统通常由光源、物镜、频率滤波器、傅里叶变换透镜、像方透镜等组成。

光源产生的光通过物镜投射到目标物体上，然后被反射或透过物体后再次通过物镜进入系统。

接着，通过一系列频率滤波器进行频率筛选，将所需的频率成分传递给傅里叶变换透镜，进而通过像方透镜成像得到频域图像。

通过反傅里叶变换可以将频域图像转换为原始图像。

傅里叶变换光学系统具有高分辨率、高灵敏度、高速度等优点，广泛应用于图像处理、成像、光学检测等领域。

- 1 -。

傅里叶光学变换
傅里叶光学变换是一种将光学信号从时域转换到频域的数学工具。

它通过将光学信号分解为不同的频率成分，可以帮助我们更好地理解和分析光学现象。

傅里叶光学变换基于傅里叶变换的原理，在光学领域广泛应用于光波的传播、衍射和成像等问题。

通过傅里叶光学变换，我们可以把一个光学信号表示为一系列不同频率的正弦波的叠加，这些正弦波的振幅和相位信息可以提供有关原始信号的详细特征。

傅里叶光学变换的数学公式如下：
F(ν) = ∫f(t)e^(-2πiνt)dt
其中，F(ν)表示频率为ν的光学信号的傅里叶变换结果，f(t)表示原始光学信号，e为自然对数的底。

傅里叶光学变换的一个重要应用是光学成像。

通过将光场的复振幅进行傅里叶变换，可以获得物体的光学频谱信息，从而实现对物体的高分辨率成像。

此外，傅里叶光学变换还可以应用于光衍射、光波前传播和信号处理等方面。

通过分析不同频率成分的振幅和相位信息，我们可以了解光场在不同空间位置和时间点的变化规律，从而对光学现象进行更深入的研究。

总之，傅里叶光学变换是光学领域中一种重要的数学工具，它能够帮助我们从频域的角度来理解和分析光学信号的特性和行为，为光学研究和应用提供了有力的支持。

傅里叶光学全复习资料1 傅里叶变换F f _ , f y f _, y e2i f_ _ fy y d_dy F{f (_, y )}式中H 0 (f_,fy)f_ 和 fy 称为空间频率，F f_ , f yF f_ , f y出瞳重叠面积 (f_, fy) 出瞳总面积 0称为 F(_,y)的傅里叶谱或空间频谱。

F (f_,fy)和 F(_,y)分别称为函数 f(_,y)的振幅谱和相位谱，而称为 f(_,y)的功率谱。

2 逆傅里叶变换f ( _, y )F ( f_ , fy )e[ 2 i ( f _ _ f y y )f_fy F 1 {F ( f_ , fy )}3 函数 f(_,y)存在傅里叶变换的充分条件是： f(_,y)必须在 _y 平面上的每一个有限区域内局部连续，即仅存在有限个不连续结点 f(_,y)在 _y 平面域内绝对可积 f(_,y)必须没有无穷大间短点4 物函数 f(_,y)可看做是无数振幅不同，方向不同的平面线性叠加的结果5 sinc 函数常用来描述单缝或矩孔的夫琅禾费衍射图样6 在光学上常用矩形函数不透明屏上矩形孔，狭缝的透射率7 三角状函数表示光瞳为矩形的非相干成像系统的光学传递函数8 高斯函数常用来描述激光器发出的高斯光束，又是用于光学信息处理的“切趾术” 9 δ函数表示某种极限状态。

可用来描述高度集中的物理量。

如点电荷、点光源、瞬间电脉冲等，所以δ函数又称为脉冲函数。

δ函数只有通过积分才有定值 10 在光学上，单位光通量间隔为 1 个单位的点光源线阵之亮度可用一个一维梳状函数表示：42 非相干成像系统的截止频率是相干成像系统的两倍 43 具有像差的系统其调制传递函数只可能下降而绝不会增大，结果会使像面上光强度分布在多个空间频率处的对比率降低，这是一个具有普遍性的重要结论 44 在相干照明条件下，光学成像系统对光场的复振幅变换而言，是线性不变系统；对于光强度的变换，则不是线性系统。