力法的原理与方程

1第六章力法2一. 力法的基本未知量和基本体系力法计算的基本思路：把超静定结构的计算问题转化为静定结构的计算问题，即利用已经熟悉的静定结构的计算方法来达到计算超静定结构的目的。

6-1 力法的基本原理3力法思路基本结构待解的未知问题qEI EIqEIX 1基本体系基本未知量01=Δ基本方程41111=+=P ΔΔΔ11111X Δδ=01111=+⋅P ΔX δ力法方程力法方程P 1Δ其中δ11和Δ1P可图乘法获得；由此确定约束力X 1，通过叠加求内力；超静定问题变成静定问题。

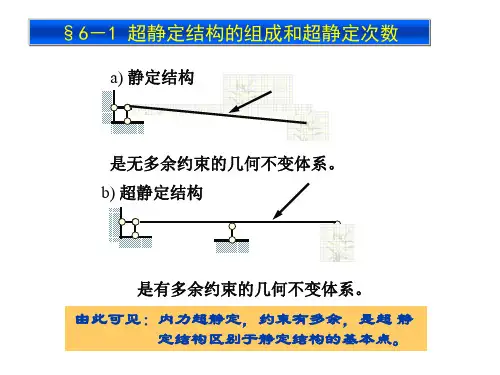
q1X Δ11=X 11δqEIqEIX 11=Δ5)力法是将多余未知力作为基本未知量的分析方法。

)将全部多余约束去掉得到的静定结构称力法的基本结构。

)根据原结构的变形条件而建立的位移方程称力法基本方程。

在变形条件成立条件下，基本体系的内力和位移与原结构相同。

1111=+⋅P ΔX δ6基本结构X 1例：基本体系PV ΔB 1==原结构已知的X 1方向的位移原结构70V ΔB 1==基本结构在X 1和外荷载P 分别作用下的变形：X 111ΔPP1Δ原结构已知的X 1方向的位移基本结构在X 1方向的位移1P 11Δ+Δ1P 11Δ+Δ0=11111X Δδ=11=X 11δ01111=Δ+P X δ力法基本方程的物理意义：基本结构在X 1和外荷载P 共同作用下，在B 点的竖向位移之和＝原结构已知的在B 点的竖向位移（等于零）。

8一个超静定结构可选的力法基本结构往往不只一种。

X 1表示原结构支座B 截面的弯矩。

基本体系二基本体系二选取：原结构PPX 1基本结构Δ1=原结构在B 点左右两截面的相对转角等于零9基本结构:PX 11PΔ11ΔB11111X δ=Δ0ΔX δ=+1P 111基本体系在X 1 和外荷载P 共同作用下，在B 点左右两截面的相对转角之和＝原结构已知的在B 点左右两截面的相对转角（等于零）1P11Δ+Δ0=10（1）（2）（1）基本结构的图和图好绘。

力法和位移法的基本方程力法和位移法是结构力学中常用的两种分析方法。

力法是以外力为基础，通过计算结构内力来求解结构的变形和应力状态；位移法则是以结构变形为基础，通过计算结构位移来求解结构的内力和应力状态。

两种方法各有优缺点，应根据具体情况选择合适的方法进行分析。

力法的基本方程为平衡方程和应力-应变关系式。

平衡方程是指结构受到的外力与内力的平衡关系，可以用以下公式表示：∑F = 0其中，∑F表示结构受到的所有外力的合力，等于内力的合力。

这个方程可以用来计算结构的内力分布。

应力-应变关系式是指材料的应力与应变之间的关系，可以用以下公式表示：σ = Eε其中，σ表示应力，E表示弹性模量，ε表示应变。

这个方程可以用来计算结构的应力分布。

位移法的基本方程为位移-力关系式和应力-应变关系式。

位移-力关系式是指结构的位移与内力之间的关系，可以用以下公式表示：u = ∑(k_i)^(-1)F_i其中，u表示结构的位移，k_i表示第i个节点的刚度，F_i表示第i个节点的外力。

这个方程可以用来计算结构的内力分布。

应力-应变关系式同样适用于位移法，可以用来计算结构的应力分布。

需要注意的是，力法和位移法的基本方程只是分析结构的起点，具体的分析方法和计算过程还需要根据具体情况进行选择和确定。

同时，结构的材料性质、几何形状、边界条件等因素也会对分析结果产生影响，需要进行综合考虑。

总之，力法和位移法是结构力学中常用的两种分析方法，它们的基本方程为平衡方程和应力-应变关系式、位移-力关系式和应力-应变关系式。

在实际分析中，应根据具体情况选择合适的方法进行分析，并考虑结构的材料性质、几何形状、边界条件等因素。

第二节 力法的基本原理及典型方程力法是计算超静定结构的最基本方法。

采用力法求解超静定结构问题时，不能孤立地研究超静定问题，而是应该把超静定问题与静定问题联系起来，即利用已经熟悉的静定结构计算方法来达到计算超静定结构的目的。

一、力法的基本原理这里先用一个简单的一次超静定结构为例来说明力法的基本概念，即讨论如何在静定结构的基础上，进一步寻求计算超静定结构的方法。

1、力法的基本未知量、基本结构和基本体系图7-7(a)所示为一次超静定梁结构，若将B 处支座链杆作为多余约束去掉，则能得到静定的悬臂梁结构（图7-7(b)）。

将原超静定结构中去掉多余约束后所得到的静定结构，称为力法的基本结构。

所去掉的多余约束处，以相应的多余未知力1X 来表示其作用，如图7-7(b)所示，这样原结构就相当于基本结构同时受到已知外荷载q 和多余未知力1X 的共同作用。

基本结构在原荷载和多余未知力共同作用下的体系称为力法的基本体系。

在基本体系中，仍然保留原结构的多余约束反力1X ,，只是把它由被动的支座反力改为主动力。

因此基本体系的受力状态与原结构是完全相同的，基本体系完全可以代表原超静定结构。

在基本体系中，只要能够设法求出1X ，则剩下的问题就是静定结构的问题了。

由此可知，力法的主要特点就是把多余未知力的计算问题当作超静定问题的关键问题，把多余未知力当作处于关键地位的未知力，因此多余未知力称为力法的基本未知量，力法这个名称就是由此而来的。

图7-7 力法的基本结构和基本体系(a)原超静定结构 (b)基本结构 (c)基本体系2、力法方程的建立怎样才能求出图7-7(c)中基本未知量1X 呢？在基本体系中，未知力1X 相当于外荷载，因此无论1X 为多大，只要梁不破坏，都能够满足平衡条件，显然不能利用平衡条件求解1X ，必须补充新的条件。

为此，将图7-7(c)中的基本体系与图7-7(a)中的原超静定结构加以比较。

在图7-7(a)所示的原超静定结构中，1X 表示支座B 处的约束反力，它是被动的，是固定值，与1X 相应的位移1 （即B 点的竖向位移）等于零。

力法典型方程力法典型方程是物理学中经常用到的方程，它描述了物体受力和相应运动的关系，是力学基本原理的具体应用。

下面介绍几个力法典型方程的例子：1. 牛顿第二定律：F = ma这是力学中最基本的方程之一。

它表明，物体的加速度与物体所受的合外力成正比，质量越大，加速度越小；质量越小，加速度越大。

这个方程揭示了物体运动的原因是受到力的作用。

2. 万有引力定律：F = G * (m?m?) / r2这是描述物体间引力作用的方程，其中F表示物体之间的引力，m?和m?分别是两个物体的质量，r是它们之间的距离，G是一个常数，称为万有引力常数。

这个方程告诉我们，两个物体之间的引力与它们的质量成正比，与它们之间的距离的平方成反比。

3. 功率方程：P = F * v这个方程描述了力的功率和物体的速度之间的关系。

功率表示单位时间内所做的功，F是作用在物体上的力，v是物体的速度。

这个方程告诉我们，功率与力和速度成正比，当力和速度增大时，功率也相应增大。

4. 胡克定律：F = k * x这个方程用于描述弹簧的伸缩过程中的力和位移之间的关系。

其中F 表示弹簧受到的恢复力，k是弹簧的弹性系数，x是弹簧的位移。

这个方程告诉我们，弹簧的恢复力与它的位移成正比。

5. 速度-时间关系方程：v = u + at这个方程描述了物体的速度和时间之间的关系，其中v是物体的最终速度，u是初始速度，a是物体的加速度，t是经过的时间。

这个方程告诉我们，物体的速度随时间的增加而改变，其改变率与加速度成正比。

这些力法典型方程是物理学中最常用的方程之一，它们可以帮助我们理解物体受力和相应运动的规律。

通过应用这些方程，我们可以计算物体的加速度、速度、力、功率等物理量，并预测物体的运动轨迹和相互作用。

在实际问题中，我们可以根据具体情况选用适当的力法典型方程来求解。

通过运用这些方程，我们能够更好地理解和解释物体的运动规律，为科学研究和工程实践提供重要的理论基础。

飞行器结构力学基础李亚智航空学院·航空结构工程系第4章力法4.1 概述静不定（超静定）结构具有“多余”未知力。

多余未知力（内力或支反力）是由多余约束引起的，也叫做多余约束力。

静不定结构中的多余未知力不能仅由平衡条件求出，而必须引入变形协调条件后才能求解。

力法是计算静不定结构内力和位移的一种基本方法。

力法的基本未知量是力—多余未知力。

4.2 力法原理及力法典型方程力法计算的基本思路：把静不定结构的计算问题转化为静定结构的计算问题，即利用静定结构的计算方法来达到求解静不定结构的目的。

P例1、图示三支点梁A B C一次静不定，有一个多余约束。

B AC P X（2）把多余约束对梁的作用（约束力）用集中力X 表示。

（1）先去掉一个多余约束（譬如可动铰支座B ）。

材料力学的求解方法：去掉多余约束后所得到的静定结构称为力法的基本系统。

本例的基本系统就是一根简支梁。

X 就是多余未知力（多余约束力），只要知道它的大小，就可以应用平衡条件求出原结构系统的支反力和内力（剪力和弯矩）的大小与分布。

A C PB 原系统基本系统A B C PAC X BX∆（3）借助变形几何关系求解多余未知力上式即为力法求解的典型方程（正则方程）。

变形几何关系：0=∆+∆=∆X P B 令为仅在X = 1作用下其作用点的位移，则1δX X ⋅=∆1δ变形几何关系成为：1=⋅+∆X P δA C PB P∆0=∆BP 1P 212例2、二次静不定桁架，共11根杆。

基本系统以两个斜杆1和2的内力作为多余未知力。

解：将两杆切开，等于去掉了两个多余约束，变成静定结构，也就是构成一个基本系统。

12原系统=++P 1P 212原状态P 1P 2载荷状态X 1多余未知力状态1X 2多余未知力状态2外载荷和多余未知力均可看作是作用于基本系统上的外力。

上页图中有以下几层含义：•原结构中多余未知力X1和X2是被动力（由外力引起），而在基本系统中是以主动力（外力）的形式出现的。

力法典型方程是根据平衡条件得到的力学是研究物体在相互作用下的运动规律的学科。

在力学中，我们经常需要使用一些数学工具来描述物体的运动状态和相互作用。

其中，力法典型方程是一种非常重要的数学工具，它可以帮助我们更好地理解物体的运动规律和相互作用。

力法典型方程是根据平衡条件得到的。

在物体的运动过程中，如果物体处于平衡状态，那么物体所受的所有力的合力应该为零。

这就是平衡条件。

根据平衡条件，我们可以得到力法典型方程。

力法典型方程的一般形式为F=ma，其中F表示物体所受的合力，m表示物体的质量，a表示物体的加速度。

这个方程告诉我们，物体所受的合力和物体的质量之间存在一种关系，这种关系可以用加速度来表示。

如果我们已知物体的质量和所受的合力，那么我们就可以通过这个方程来计算物体的加速度。

反之，如果我们已知物体的质量和加速度，那么我们也可以通过这个方程来计算物体所受的合力。

除了一般形式的力法典型方程，还有一些特殊形式的力法典型方程，比如牛顿第二定律和牛顿第三定律。

牛顿第二定律可以表示为F=ma，它告诉我们，物体所受的合力和物体的质量之间存在一种直接的关系。

牛顿第三定律可以表示为F1=-F2，它告诉我们，物体之间的相互作用是相互的，即每个物体所受的力都与另一个物体所施加的力大小相等、方向相反。

力法典型方程在物理学和工程学中都有广泛的应用。

在物理学中，它可以用来描述物体的运动规律和相互作用。

在工程学中，它可以用来设计和优化各种机械系统。

比如，我们可以用力法典型方程来计算汽车的加速度和制动距离，来优化机械结构的设计，以达到更高的效率和更好的性能。

总之，力法典型方程是一种非常重要的数学工具，它可以帮助我们更好地理解物体的运动规律和相互作用。

通过平衡条件，我们可以得到这个方程的一般形式，也可以得到一些特殊形式的方程。

这个方程在物理学和工程学中都有广泛的应用，为我们研究和设计各种机械系统提供了有力的支持。