下载文档原格式
力法典型方程什么是力法典型方程？我们在物理学中经常会遇到关于力的问题，而力法典型方程就是解决这些问题时常常用到的数学方程。
通过运用力法典型方程，我们能够更加准确地描述和分析物体受力的情况，进而解决各类与力相关的问题。
下面我们就来一起了解一下力法典型方程是怎样发挥作用的吧。
在物理学中，力是改变物体运动状态的原因。
根据牛顿第二定律，一个物体受到的力的大小与物体的质量和运动加速度成正比，符号表示为F=ma。
这就是最典型的力法方程之一。
在这个方程中，F代表力的大小，m代表物体的质量，a代表物体的加速度。
在日常生活中，我们经常会遇到需要计算力的问题。
例如，当我们用力推动一个物体时，我们需要计算所施加的力的大小。
这时，我们可以通过使用力法典型方程来解决这个问题。
我们首先要确定物体的质量，然后通过测量物体的加速度，就能够求出施加的力的大小。
这个方法能够帮助我们准确地计算出所需要的力的大小，从而更好地完成推动物体的任务。
除了F=ma以外，力法典型方程还包括其他一些常见的方程。
例如，当我们需要计算物体所受重力时，我们可以使用F=mg，其中g表示重力加速度。
这个方程告诉我们，物体受到的重力的大小等于物体的质量乘以重力加速度。
通过这个方程，我们可以计算出物体所受的重力，从而更好地理解物体的运动状态和受力情况。
力法典型方程的运用不仅仅局限于平面运动问题，还能够应用于其他与力有关的物理学领域。
例如，在静力学中，我们可以通过应用平衡条件和公式F=0，找到物体处于平衡状态时所受到的力的关系。
这个方程告诉我们，当一个物体处于平衡状态时，物体所受的合力为零。
通过运用这个方程，我们能够判断物体是否处于平衡状态，并进一步分析物体所受的各个力的大小和方向。
力法典型方程在物理学中具有很大的指导意义。
它不仅帮助我们更好地理解和描述物体受力的情况，更能够指导我们解决各类与力相关的问题。
通过熟练掌握和运用力法典型方程，我们能够提高解题的准确性和效率，更好地解决复杂的物理问题。
力法典型方程柔度系数力法典型方程是材料力学研究中常用的一种表示方法，它能够描述材料受力时的本质特征。
在力法典型方程中，柔度系数是一个重要的物理量，用于表示材料在受力时的弹性特性。
什么是柔度系数？柔度系数是材料力学中一个很重要的物理量，这个物理量可以用于描述物体在受力时的弹性特性。
简单来说，所谓柔度系数就是物体受外力作用下形变产生的应力与应变的比值。
柔度系数通常以弹性模量为基础，而它的倒数就是物体的刚度系数。
在实际应用中，弹性模量是一种非常重要的材料力学参数，用于描述弹性材料在受力时的本质特征，而柔度系数正是弹性模量的倒数。
因此，柔度系数可以用于描述材料某种特定的力学行为，包括弹性变形的程度、刚度等等。
比如，弹簧就是一种典型的弹性材料，它的涵盖了所有的形变应力和变形的比值，意味着弹簧受到的力越大，形变就越大。
因此，柔度系数可以用来衡量弹簧的弹性能力。
柔度系数在力法典型方程中的应用力法典型方程是材料力学研究中常用的一种表示方法，用于描述材料在受力时的本质特征。
在力法典型方程中，柔度系数是一个很重要的物理量，用于描述材料在受力时的弹性特性。
力法典型方程通常表示为f(x) = kx，其中x是材料的位移，k是柔度系数。
当物体受力时，它会发生形变，并且会产生反作用力来抵消外力。
而柔度系数就是描述物体在受力时的弹性特性的一个重要参数。
比如，当有一个物体受到一个力F作用时，它发生的形变量可以用弹性模量E来表示，而它的弹性形变量可以用材料的柔度系数k来表示。
柔度系数的大小通常与材料质地和处理过程有着密切的关系。
对于弹性材料来说，柔度系数越大，材料的弹性变形量就越大，材料受到的应力也越小。
因此，柔度系数越大的材料，越容易发生弹性变形。
结论柔度系数是材料力学研究中的一个重要物理量，它用于描述材料在受力时的弹性特性。
在力学研究中，柔度系数通常与弹性模量密切相关，它可以用来衡量物体受到外力时的形变程度和弹性能力。
在力法典型方程中，柔度系数被用来描述物体在受力时的弹性特性，它是该方程模型的一个关键参数。
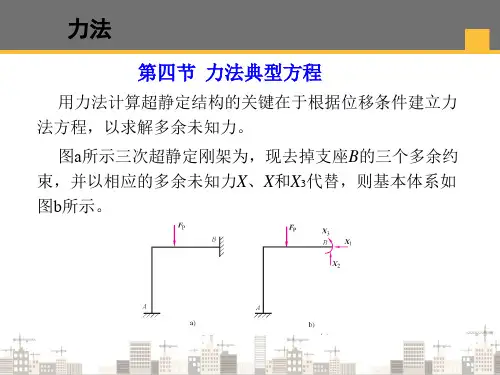
位移法的典型方程与力法的典型方程一样位移法和力法是结构分析中常用的两种方法。
位移法是通过求解结构的位移来得到结构的反力，而力法是通过已知的外力和支座反力来求解结构的内力和位移。
尽管这两种方法的思想和计算过程不同，但它们的本质是相同的，都是基于平衡原理和变形原理，因此它们的典型方程也具有相似性。
一、位移法的典型方程位移法是一种基于变形原理的方法，它假设结构的变形是已知的，通过求解结构的位移来得到结构的反力。
位移法的典型方程是：$$boldsymbol{K}boldsymbol{u}=boldsymbol{F}$$其中，$boldsymbol{K}$是结构的刚度矩阵，$boldsymbol{u}$是结构的位移向量，$boldsymbol{F}$是结构的外力向量。
在这个方程中，$boldsymbol{u}$是未知量，$boldsymbol{K}$和$boldsymbol{F}$是已知量。
因此，通过求解这个方程，可以得到结构的位移和反力。
二、力法的典型方程力法是一种基于平衡原理的方法，它假设结构的外力和支座反力是已知的，通过求解结构的内力和位移来满足平衡条件。
力法的典型方程是：$$boldsymbol{K}boldsymbol{x}=boldsymbol{P}$$其中，$boldsymbol{K}$是结构的刚度矩阵，$boldsymbol{x}$是结构的位移向量，$boldsymbol{P}$是结构的等效节点力向量。
在这个方程中，$boldsymbol{x}$是未知量，$boldsymbol{K}$和$boldsymbol{P}$是已知量。
因此，通过求解这个方程，可以得到结构的内力和位移。
三、位移法和力法的相似性位移法和力法的本质是相同的，它们都是基于平衡原理和变形原理的。
因此，它们的典型方程也具有相似性。
首先，它们的典型方程都是线性方程组。
在位移法和力法中，结构的刚度矩阵和等效节点力向量都是已知的，未知量是结构的位移和反力（力法中是内力和位移）。
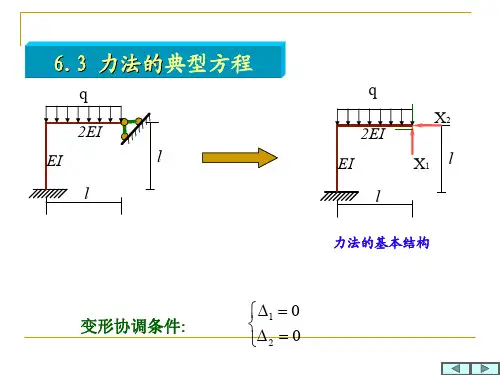
力法典型方程力法典型方程是物理学中经常用到的方程，它描述了物体受力和相应运动的关系，是力学基本原理的具体应用。
下面介绍几个力法典型方程的例子：1. 牛顿第二定律：F = ma这是力学中最基本的方程之一。
它表明，物体的加速度与物体所受的合外力成正比，质量越大，加速度越小；质量越小，加速度越大。
这个方程揭示了物体运动的原因是受到力的作用。
2. 万有引力定律：F = G * (m?m?) / r2这是描述物体间引力作用的方程，其中F表示物体之间的引力，m?和m?分别是两个物体的质量，r是它们之间的距离，G是一个常数，称为万有引力常数。
这个方程告诉我们，两个物体之间的引力与它们的质量成正比，与它们之间的距离的平方成反比。
3. 功率方程：P = F * v这个方程描述了力的功率和物体的速度之间的关系。
功率表示单位时间内所做的功，F是作用在物体上的力，v是物体的速度。
这个方程告诉我们，功率与力和速度成正比，当力和速度增大时，功率也相应增大。
4. 胡克定律：F = k * x这个方程用于描述弹簧的伸缩过程中的力和位移之间的关系。
其中F 表示弹簧受到的恢复力，k是弹簧的弹性系数，x是弹簧的位移。
这个方程告诉我们，弹簧的恢复力与它的位移成正比。
5. 速度-时间关系方程：v = u + at这个方程描述了物体的速度和时间之间的关系，其中v是物体的最终速度，u是初始速度，a是物体的加速度，t是经过的时间。
这个方程告诉我们，物体的速度随时间的增加而改变，其改变率与加速度成正比。
这些力法典型方程是物理学中最常用的方程之一，它们可以帮助我们理解物体受力和相应运动的规律。
通过应用这些方程，我们可以计算物体的加速度、速度、力、功率等物理量，并预测物体的运动轨迹和相互作用。
在实际问题中，我们可以根据具体情况选用适当的力法典型方程来求解。
通过运用这些方程，我们能够更好地理解和解释物体的运动规律，为科学研究和工程实践提供重要的理论基础。
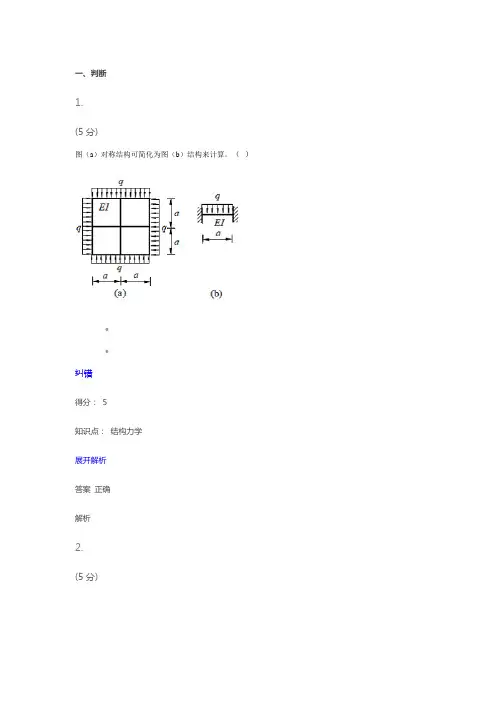
一、判断1.(5分)图（a）对称结构可简化为图（b）结构来计算。
（）••纠错得分：5知识点：结构力学展开解析答案正确解析2.(5分)图示对称刚架，在反对称荷载作用下，半边结构图（c）所示。
（）••纠错得分：5知识点：结构力学展开解析答案错误解析3.(5分)图示简支斜梁，在荷载P作用下，若改变B支座链杆方向，则梁的内力将是M、N不变，Q改变。
（）••纠错得分：5知识点：3.2 多跨静定梁的内力分析展开解析答案错误解析4.(5分)计算图示桁架中指定杆件内力，各杆EA=常数，N2=−P/2。
（）••纠错得分：5知识点：结构力学展开解析答案正确解析5.(5分)图（a）所示桁架结构可选用图（b）所示的体系作为力法基本体系。
（）••纠错得分：5知识点：结构力学展开解析答案正确解析6.(5分)图示对称结构，EI=常数;较简便的力法基本结构如图所示。
（）••纠错得分：5知识点：结构力学展开解析答案正确解析7.(5分)图示结构中杆AC由于加热伸长了Δ，则杆AB的变形是0。
（）••纠错得分：5知识点：结构力学,3.3 静定平面刚架的内力分析展开解析答案正确解析8.(5分)图示结构EI=常数，求K点的竖向位移时，由图乘法得:ΔK=（1/EI）×y1ω1。
（）••纠错得分：5知识点：结构力学展开解析答案错误解析9.(5分)图示体系的几何组成为几何不变，无多余联系。
（）••纠错得分：5知识点：结构力学展开解析答案正确解析10.(5分)图示为一刚架的力法基本体系，E=常数。
其δ12为EI/8。
（）••纠错得分：5知识点：结构力学展开解析答案错误解析11.(5分)图示刚架，EI=常数，B点的竖向位移（↓）为Pl3/（6EI）。
（）••纠错得分：5知识点：结构力学,3.3 静定平面刚架的内力分析展开解析答案错误解析12.(5分)下图能用力矩分配法计算。
（）••纠错得分：5知识点：结构力学展开解析答案错误解析13.(5分)图示结构EI=常数，在给定荷载作用下，固定端的反力矩为，逆时针旋转。
