当前位置：文档之家 › 结构力学力法典型方程

结构力学力法典型方程

  • 格式：ppt
  • 大小：112.50 KB
  • 文档页数：6

下载文档原格式

  / 6

合集下载

结构力学教程——第10章 力法

结构力学教程——第10章 力法

系数和自由项 ➢ 梁、刚架：
ii
M i 2 ds
EI
Ai yi EI
ij
M i M j ds EI
Aj yi EI
iP
M i M P ds EI
➢ 桁架：
2
ii
Ni l EA
ij
Ni N jl EA
iP
Ni N Pl EA
知识点
10.3 超静定刚架和排架
1. 刚架
20kN/m
11
M12 EI
ds
FN21 EA
ds
y2
cos2
EI ds EA ds
1P
M1 M P EI
ds
M0y ds
EI
（4）求多余未知力，即水平推力FH
M0y
X1
FH
1P 11
y2 EI
EI ds
cos2
ds EA
ds
（5）内力计算
M M 0 FH y
FQ FQ0cos FHsin FN FQ0sin FHcos
1P 11X1 0
P
2P 0
P
0
a
11
2 2
1
1
1
P
a
N1
NP
(3)求系数
11
2
Ni l 2( EA
2)2 EA
2a 4 12 a EA
4a (1 EA
2)
1P
Ni N jl 1 Pa 2 EA EA
(
2 )( EA
2P)
2a 2Pa (1 EA
2)
(4)解方程
X1
1P
11
P 2
当结构框格数目为 f , 则 n=3f 。

力 法的基本原理和典型方程

力 法的基本原理和典型方程

l3
3
1
ql 4
8
0
Χ1
3 8
ql
多余未知力X1求出后,其余所有反力和内力都可用静 力平衡条件确定，内力图如图5.10所示。
图5.10
结构任一截面的弯矩也可用叠加原理表示为
Μ Μ1Χ1 ΜF
M 1——单位力 1 1 作用下在基本结构 中任一截面上所产生的弯矩
Μ
——
F
荷
载
作
用
下
基
本
结
构
中
同
一
（c） 图5.8
（d）
一次超静定结构的力法基本方程：11Χ1 1F 0
1 1称为系数，1F称为自由项，它们的物理意义分别如
图5.9（a）、（b）所示
（a） q
（b） 图5.9
可绘出基本结构在单位力 1 1作用下的弯矩图 Μ 1 [图 5.9(c)]和荷载单独作用下的弯矩图 Μ F [图5.9(d)]应用图
位移的地点
产生位移的原因
对于梁和刚架在不计剪力和轴力的影响时，可按下
式计算或用图乘法计算：
2
δii
M i ds l EI
δij
M i M j ds l EI
iF
M iMF ds l EI
Μ i 、Μ j 、M F分别代表X i 1和 X j 1 荷载单独作用
于基本结构中的弯矩。
结构力学
图5.12
力法的典型方程：
δ11Χ1 δ12 Χ2 … δ1i Χi … δ1n Χn 1F 0 δ21Χ1 δ22 Χ 2 … δ2i Χi … δ2n Χn 2F 0
…
δn1Χ1 δn2 Χ2 … δni Χi … δnn Χn nF 0

结构力学第4章 力法计算简化.

结构力学第4章 力法计算简化.

FP
2
FP
单位弯矩（图）和荷载弯矩（图）为：
FP R
FP 2
FP R
FP
FP R

FP
M1 1
MP


FP R 2
sin
若只考虑弯矩对位移的影响，有：
11


M12ds EI

R
2EI
,
1 P

M1M Pds EI


FP R2 2EI
,
X1

FP R

弯矩为：
M

M1 X1

MP
FP /4 FP /2 FP /4
FP /4 FP /2 FP /4 FP /4 FP /2 FP /4
FP /4 FP /4
FP /4
I/2
FP /4
FP /4
又看到您了！ FP /4 FP /4
FP /4
I/2
I/2
二、 使单位弯矩图限于局部
ij ji 0 i 1,, n 2
3. 力法计算的简化
无弯矩状态的判别
前提条件：结点荷载； 不计轴向变形。 刚结点变成铰结点后，体系仍然几何不变的情况
刚结点变成铰结点后，体系几何可变。但是，添 加链杆的不变体系在给定荷载下无内力的情况
利用上述结论，结合对称结构的对称性，可使 手算分析得到简化。
一、 对称性 (Symmetry) 的利用
P
例： FP
FP
由于 0 ，问题无法化简 12
（2）未知力分组和荷载分组
FP
X1 Y1 Y2 , X2 Y1 Y2 , 12 0
力法典型方程成为：

结构力学：第七章 力法

结构力学：第七章 力法

A
B
两铰拱，一次超静定结构。
A
B
一次超静定桁架
A
B
曲梁，静定结构。
A
B
静定桁架
§7-2 超静定次数的确定
去掉几个约束后成为静 定结构,则为几次超静定
X1 X2 X3 X1 X2 X3
X1 X2 X3
去掉一个链杆或切断一个链杆相 当于去掉一个约束
§7-2 超静定次数的确定
（2）去掉一个铰支座或一个单铰，等于拆掉两个约束。
以位移作为基本未知量，在自动满足变形协调条件 的基础上来分析，当然这时主要需解决平衡问题，这 种分析方法称为位移法（displacement method）。
3. 混合法----以结点位移和多余约束力作为 基本未知量
如果一个问题中既有力的未知量，也有位移的未 知量，力的部分考虑位移协调，位移的部分考虑力 的平衡，这样一种分析方案称为混合法（mixture method）。
思考：多余约束是多余的吗？
从几何角度与结构的受力特性和使用要求两方面讨论。
q
q
A
B
A
B
C
l
A
B
q l2 8
超静定结构的优点为:
0.5l
A
ql 2 64
0.5l
q l2
32
B
C ql 2
64
1. 内力分布均匀 2. 抵抗破坏的能力强
§7-1 超静定结构概述
二、超静定结构的类型
超静定梁 超静定刚架 超静定拱
A
C
D
B
A
CD
B
F E
以五个支座链杆为多余约束
其它形式的静定刚架：
AA
CC KK DD

结构力学——力法

结构力学——力法
X1 = 9ql / 20, X 2 = 3ql / 40
X1 X2
ql 2 / 40 M
∆1 = 0 ∆ 2 = 0 δ11 ⋅ X1 + δ12 ⋅ X2 + ∆1P = 0 δ21 ⋅ X1 +δ22 ⋅ X2 + ∆2P = 0
q
X1 = −3ql / 20, X 2 = −ql 2 / 40
将未知问题转化为 已知问题， 已知问题，通过消除已 知问题和原问题的差别， 知问题和原问题的差别， 使未知问题得以解决。 使未知问题得以解决。 这是科学研究的 基本方法之一。 基本方法之一。
二.力法的基本体系与基本未知量 力法的基本体系与基本未知量 超静定次数: 超静定次数: 多余约束个数.
若一个结构有N个多余约束,则称其为N次超静定结构. . 几次超静定结构? 几次超静定结构
X
= 3 ql / 8 ( ↑ )
⋅ X
+ M
P
ql
2
/ 2
l
MP
M1
力法步骤: 力法步骤: 1.确定基本体系 4.求出系数和自由项 确定基本体系 求出系数和自由项 2.写出位移条件 力法方程 写出位移条件,力法方程 5.解力法方程 写出位移条件 解力法方程 3.作单位弯矩图 荷载弯矩图 6.叠加法作弯矩图 作单位弯矩图,荷载弯矩图 作单位弯矩图 荷载弯矩图; 叠加法作弯矩图 练习 P EI l EI l 作弯矩图. 作弯矩图
M1
3 Pl 8 5 Pl 8
=0 δ 11 = 4l / 3EI ∆1P = − Pl 3 / 2 EI
X 1 = 3 P / 8(↑)
M = M1 ⋅ X 1 + M P
P
MP

结构力学力法的典型方程

结构力学力法的典型方程

结构力学力法的典型方程结构力学是研究结构内部受力和变形规律的学科，通过建立力学模型并利用力学方程进行分析，可以预测结构的受力状态和稳定性。

在结构力学中，主要涉及到几个典型的方程，包括平衡方程、变形方程和材料本构关系方程。

1.平衡方程：平衡方程是表达结构处于静力平衡状态的基本方程，根据牛顿第二定律可得出。

平衡方程可以分为整体平衡方程和局部平衡方程。

（1）整体平衡方程：整体平衡方程是研究整个结构的受力平衡关系，通常包括平衡条件、力的平衡方程和力矩的平衡方程。

2.变形方程：变形方程是用来描述结构受力引起的变形情况的方程，包括位移方程和应变-位移关系。

（1）位移方程：位移方程是用来描述结构各点的位移与受力之间的关系。

位移方程可以根据变形模型和平衡条件来推导，一般采用构件的柔度矩阵或势能法推导。

（2）应变-位移关系：应变-位移关系是研究结构变形与应变之间的关系，通过该关系可以求解结构的受力和变形情况。

应变-位移关系通常根据材料的本构关系来确定。

3.材料本构关系方程：材料本构关系方程是研究结构材料特性对结构力学性能的影响，通过该方程可以获得应力-应变关系。

材料本构关系方程根据材料的力学性质和实验数据来确定，常用的材料本构关系方程有钢材的线弹性本构关系、混凝土的受压和受拉本构关系等。

在结构力学中，以上三个典型方程通常以矩阵形式来表达，从而可以进行更加简洁和高效的数值计算。

典型的矩阵方程包括平衡方程的矩阵形式、位移方程的矩阵形式、应变-位移关系的矩阵形式以及材料本构关系方程的矩阵形式等。

总结起来，结构力学的典型方程包括平衡方程、变形方程和材料本构关系方程。

这些方程是结构力学分析的基础，通过这些方程的建立和求解，可以揭示结构内部受力和变形的规律，为结构的设计和优化提供依据。

结构力学第六章力法

结构力学第六章力法

弯矩图可按悬臂梁画出
M X1 M 1 M P
§6-4 力法计算超静定桁架和组合结构
一 超静定桁架
F Ni l ii EA F N i F N jl ij EA F N i FN P l iP EA
2
桁架各杆只产生轴力,系数
典型方程: 11 X 1 1P 0
9 17 FP , X 2 FP 80 40
叠加原理求弯矩： M X 1 M 1 X 2 M 2 M P
3FPL/40 3FPL/40
FP 9FP/80
23FP/40 FNDC
FQDC 3FPL/80 FQBD
FQCD FNDA
FQBD=-9FP/80
FNBD=-23FP/40
FQDC=3FP/40+FP/2=23FP/40
2 P 3P 0
11 X 1 1P 0 22 X 2 23 X 3 0 X X 0 33 3 32 2
11 X 1 1P 0 X 2 X 3 0
反对称荷载作用下, 沿对称轴截面上正对称内力为0 例: FP FP/2 FP/2 FP/2
1）一般任意荷载作用下
11 X 1 12 X 2 13 X 3 1P 0 21 X 1 22 X 2 23 X 3 2 P 0 X X X 0 33 3 3P 31 1 32 2
11 X 1 1P 0 22 X 2 23 X 3 2 P 0 X X 0 33 3 3P 32 2
M FN
超静定结构的内力分布与梁式杆和二力杆的相对刚度有关。 链杆EA大，M图接近与连续梁，链杆EA小，M图接近与简支梁。 例: 中间支杆的刚度系数为k,求结点B的竖向位移？EI=C

《结构力学》第七章力法

《结构力学》第七章力法
A点的位移
沿X1方向：
沿X2方向：
沿X3方向：
据叠加原理，上述位移条件可写成
原结构
基本结构
△1=
（7—2）
（a）
（b）
11
21、22、23和△2P ；
31、32、33和△3P 。
△2=21X1+22X2+23X3+△2P=0 △3=31X1+32X2+33X3+△3P=0
11X1
+12X2
+13X3
11X1+12X2+△1P=0 21X1+22X2+△2P=0 33X3+△3P=0
则 X3=0 。
这表明：对称的超静定结构，在对称的荷载作用下， 只有对称的多余未知力，反对称的多余未知力必为零。
↓
↓
a
a
P
P
↓
↓
P
P
MP图
（2）对称结构作用反 对称荷载
MP图是反对称的，故
2 .确定超静定次数的方法:
解除多余联系的方式通 常有以下几种：
（1）去掉或切断一根链杆，相当于去掉一个联系。
↓
↑
（2）拆开一个单铰，相当 于去掉两个联系。
用力法解超静定结构时，首先必须确定多余联系 或多余未知力的数目。
↓
↑
←
→
多余联系或多余未知力的个数。
多余未知力：
多余联系中产生的力称为多余未 知力（也称赘余力）。
此超静定结构有一个多余联 系，既有一个多余未知力。
此超静定结构有二个多余联 系，既有二个多余未知力。
返 回
*
3. 超静定结构的类型
（1）超静定梁; （2）超静定桁架； （3）超静定拱；

《结构力学(第5版)》第7章 力法

《结构力学(第5版)》第7章 力法

§7-3 力法的基本概念
δ11—表示X1=1时，B点沿X1方向的位移，Δ11= δ11X1。
11 + 1P=0 可写为 11X1 Δ1P 0
力法基本方程
绘出基本结构在X1=1、荷载q作用下 的弯矩图，如图a、b。
11
1 EI
l2 2
2l 3
l3 3EI
Δ1P
1 EI
(1 3
l2 2
l)
ql 4 8EI
各内力图如图c、d。
基本体系
§7-5 力法的计算步骤和示例
计算系数和自由项。
11
5l 3 27 EI
Δ1P
7ql 4 216 EI
解得
X1
7 40
ql
叠加法作弯矩图 M M1 X1 M P
弯矩图如图e。
§7-6 对称性的利用
1、选取对称的基本结构
对称的意义：（1）结构的几何形状和支承情况对称 （2）各杆的刚度（EI、EA等）也对称
基本体系
典型方程为
11X1 12 X 2 13 X 3 Δ1P 0 21X1 22 X 2 23 X 3 Δ2P 0 31X1 32 X 2 33 X 3 Δ3P 0
各弯矩图如图c、d、e、f 。
因 M 3 0，FS3 0，FN1 FN2 FNP 0
故 13 31 0， 23 32 0，Δ3P 0
6次超静定
图a所示结构，在拆开单铰、切断链杆、切开刚结处后，得到图b所示静定结构 同一超静定结构，可以用不同方式去掉多余联系，如图c、d所示静定结构 对于有较多框格的结构，一个封闭无铰的框格，其超静定次数等于3。
21
16
9
次
次
次
超
超

《结构力学》第5章：力法

《结构力学》第5章：力法

03
对边界条件敏感
力法对边界条件的处理较为敏感， 边界条件的微小变化可能导致计 算结果的显著不同。
适用范围讨论
适用于线弹性结构
01
力法适用于线弹性结构，即结构在荷载作用下发生的
变形与荷载成正比，且卸载后能够完全恢复。
适用于静定和超静定结构
02 力法既适用于静定结构，也适用于超静定结构，但超
静定结构需要引入多余未知力和变形协调条件。
在传动系统的力学分析中，采用力法计算各部件的受力情况，
确保传动系统的正常运转。
案例分析与启示
力法应用广泛性
力法计算精确性
通过以上案例可以看出，力法在桥梁、建 筑和机械工程等领域具有广泛的应用价值 。
力法作为一种精确的计算方法，在解决超 静定问题方面具有显著优势。
力法在工程实践中的局限性
对未来研究的启示
《结构力学》第 力法典型方程及应用 • 力法计算过程与实例分析 • 力法优缺点及适用范围 • 力法在工程实践中应用 • 力法学习建议与拓展资源
01 力法基本概念与原理
力法定义及作用
力法是一种求解超静定结构的方法， 通过引入多余未知力，将超静定问题 转化为静定问题进行求解。
桁架结构应用
桁架结构由杆件组成，通过力法可以求解桁架结构中的多余未知力，进而分析 桁架的稳定性和承载能力。
组合结构应用
组合结构由不同材料或不同形式的构件组成，通过力法可以分析组合结构的内 力和变形，为结构设计提供优化建议。
复杂结构简化与力法应用
复杂结构简化
对于复杂结构，可以通过合理简化为静定结构或简单超静定结构，进而应用力法求解。
适用于简单和规则结构
03
对于简单和规则结构，力法能够较为方便地求解出结

结构力学 力法

结构力学 力法
k →∞ k →0
X1 = 5 ql ( ↑ ) 4 X1 = 0
当 当
求解图示加劲梁。 例 5. 求解图示加劲梁。 −4 4 横梁 I = 1 × 10 m
解： δ 11 X 1 + ∆1 P = 0
10.67 12.2 , + δ 11 = EI EA 533 .3 ∆1 P = EI 当 A = 1× 10 −3 m 2 ,
ql 2 20
1
M X1
Mi
ql 2 / 40
∆1 = 0 ∆ 2 = 0
1 1 ql 2 1 ql 2 1 ql 3 θA = ( ⋅l ⋅ ⋅1 − ⋅ l ⋅ ⋅1) = ( EI 2 20 2 40 80 EI
)
(1).位移计算 位移计算
求A截面转角 截面转角 q A ql 22EI EI 20 l M l
X1
P -P/2 a
2/2
X1 = − P / 2
P/2 a 0 0 P P
− 2P
X1 = 1
Hale Waihona Puke 1 0 1− 2 − 2
1 1 1
N1
N = N1 X1 + N P
X1
0
P
P 变形条件仍为: 变形条件仍为: N∆1 = 0 P 对吗? 对吗?
X1 X1
∆1 = −
X 1a EA
求作图示梁的弯矩图。 例 4. 求作图示梁的弯矩图。
P
Pl 2 / 8
l X1 P
l X2 X3
δ 13 = δ 31 = δ 23 = δ 32 = ∆3 P = 0
M 32ds N 32ds kQ32ds l δ 33 = ∫ +∫ +∫ = ≠0 EI EA GA EA X3 = 0 δ 11 X 1 + δ 12 X 2 + ∆1 P = 0 δ 21 X 1 + δ 22 X 2 + ∆ 2 P = 0

力法典型方程中的主系数

力法典型方程中的主系数

力法典型方程中的主系数
（最新版）
目录
1.力法典型方程的概述
2.力法典型方程中的主系数
3.主系数的正负性和零值
4.主系数的物理意义
5.结论
正文
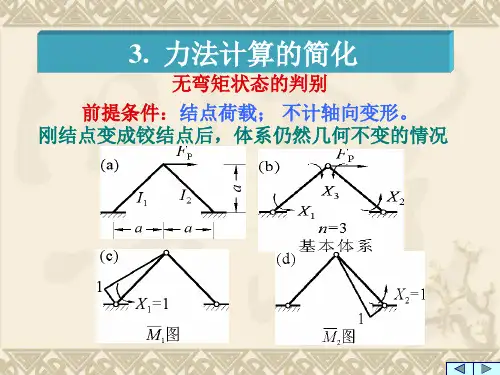
力法典型方程是一种求解结构力学中复杂问题的有效方法，它是基于静力平衡条件建立起来的。

在力法典型方程中，主系数是一个重要的概念，它在解决问题的过程中起着关键作用。

本文将从主系数的定义、正负性和零值、物理意义等方面进行详细阐述。

首先，力法典型方程是由平衡条件得到的，它是一种反映结构静力平衡条件的方程。

在这个方程中，主系数是一个重要的系数，它决定了方程的解的性质。

主系数的正负性和零值是力法典型方程求解中的重要概念。

其次，主系数的正负性决定了力法典型方程的解的性质。

如果主系数为正，则方程有唯一解；如果主系数为负，则方程无解；如果主系数为零，则方程有无穷多解。

因此，在力法典型方程求解过程中，需要首先判断主系数的正负性，以确定方程的解的性质。

此外，主系数的物理意义也非常重要。

主系数表示基本结构在荷载等外因和结点位移的共同作用下，每一个附加联系处附加反力矩或附加反力都应为零。

也就是说，主系数反映了结构在荷载作用下的位移情况，它决定了结构的稳定性和刚度。

综上所述，力法典型方程中的主系数是一个非常重要的概念，它决定
了方程的解的性质和结构的稳定性。

力法典型方程中的主系数

力法典型方程中的主系数

力法典型方程中的主系数
摘要：
I.引言
- 介绍力法典型方程
- 说明主系数的重要性
II.力法典型方程的定义和公式
- 力法典型方程的定义
- 力法典型方程的公式
III.主系数的概念和计算方法
- 主系数的定义
- 计算主系数的方法
IV.主系数的作用和意义
- 主系数在力法典型方程中的作用
- 主系数对结构分析和设计的影响
V.结论
- 总结主系数的重要性
- 强调主系数在力法典型方程中的关键作用
正文：
力法典型方程是结构力学的核心内容之一，它用于描述结构在外力作用下的变形和内力分布情况。

在力法典型方程中，主系数是一个关键的参数，它直接影响着方程的解法和结构的分析结果。

因此，对主系数的理解和掌握是力学
研究的重要一环。

力法典型方程的定义是：在给定外力作用下，结构达到平衡状态时，各杆件的弯矩、剪力、轴力等内力分布规律的数学表达式。

主系数则是这个表达式中的一个重要参数，它反映了结构在特定位置处的内力分布情况。

主系数通常由结构的形状、尺寸和材料性质等因素决定，计算方法相对复杂。

主系数的概念虽然抽象，但它对力法典型方程的解法和结构分析具有重要意义。

首先，主系数直接影响方程的解法。

在典型方程中，主系数的正负和大小决定了方程的根的性质，从而影响了方程的解法。

其次，主系数对结构的分析和设计也有重要影响。

在结构设计中，我们需要根据主系数来判断结构的稳定性和安全性，进而确定合适的结构和材料参数。

总之，主系数在力法典型方程中起着关键作用，对理解和掌握力法典型方程具有重要意义。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
§5-3力法的典型方程
先讨论两次超静定结构。
C FP
A
q B
C FP
A
q
B
X1 C X2 FP
基本体系之一
A
D11 X1 B D21
FP C A
D12
D22
B X2
C FP
A
变形条件
q
D1P
B D2P
C
q B X2
FP
X1 基本体系之二
A
Δ1 0
Δ2 0
C FP
A
q B
C FP
A
q X1 C
2）其它的系数dij（i≠j）称为副系数，它是单位多余未知力Xj=1单独
作用时所引起的沿Xi方向的位移，其值可能为正、负或零。
3）各式中最后一项DiP称为自由项，它是荷载单独作用时所引起的沿Xi
方向的位移，其值可能为正、负或零。
4）根据位移互等定理可知，在主斜线两边处于对称位置的两个副系
数dij与dji是相等的，即 dij =dji
关于系数和自由项的计算
d11X1 d12X2 d1nXn Δ1P 0
d21X1 d22X2 d2nXn Δ2P 0

dn1X1 dn2X2 dnnXn Δn P 0
1）主斜线（自左上方的d11至右下方的dnn）上的系数dii称为主系数
，它是单位多余未知力Xi=1单独作用时所引起的沿其本身方向上的 位移，其值恒为正，且不会等于零。
d11X1 d12X2 d1nXn Δ1P 0
d21X1 d22X2 d2nXn Δ2P 0

dn1X1 dn2X2 dnnXn Δn P 0
这就是n次超静定结构的力法典型方程。方程组中每一 等式都代表一个变形条件，即表示基本体系沿某一多余 未知力方向的位移，应与原结构相应的位移相等。
(a)
Δ2 Δ21Δ22Δ2P 0
D11=d11X1、D21=d21X1
D12=d12X2、D22=d22X2
代入式(a),得
Δ1d11X1d12X2Δ1P0 Δ2d21X1d22X2Δ2P0
这就是根据变形条件建立的求解两次超静定结构的 多余未知力X1和X2的力法基本方程。
图a是三次超静定结构，去掉固定支座A， 得如图b所示的基本结构。
位移条件：A处不能有任何位移。
D1= 0，D 2=0，D 3=0
X11、 X21、 X31和F分别作用于基本结构时
A点沿X1方向的位移分别为 d d d 1、 1 1、 2 1、 3 Δ1P d d d A点沿X2方向的位移分别为 2、 1 2、 2 2、 3Δ2P A点沿X3方向的位移分别为 d d d 3、 1 3、 2 3、 3 Δ3P
B X2 FP
基本体系之一
A
D11 X1 B D21
C FP
A
D12 D22
C B X2 FP
A
q
D1P
B D2P
C
q X2
B
FP X1 基本体系之二
A
根据叠加原理，上述位移条件可写为
Δ1 Δ11Δ12Δ1P 0
(a)
Δ2 Δ21Δ22Δ2P 0
因为
Δ1 Δ11Δ12Δ1P 0
位移条件可写为
Δ1d11X1d12X2d13X3Δ1P 0 Δ2 d21X1d22X2d23X3Δ2P 0 Δ3 d31X1d32X2Байду номын сангаас33X3Δ3P 0
对于n次超静定结构，则有n个多余未知力，而每一个多 余未知力都对应着一个多余约束，相应地也就有一个已 知变形条件，故可据此建立n个方程，从而可解出n个多 余未知力。当原结构上各多余未知力作用处的位移为零 时，这n个方程可写为