北师大版七年级数学上探索规律练习题一

2019-2020 学年七年级数学上册《 3.6探索规律》试题北师大版材料信息的加工提和运用，律和能反映出一个人的用数学、展数学和行数学新的意和能力。

求解探索律型要求学生有敏的察力，能从特殊的情况出，周密的思考，全面的分析，去推得一般的。

意在解者数学的新意和才能。

【命分析】例 1 日常生活中我使用的数是十制数．而算机使用的数是二制数，即数的位方法是“逢二一” ．二制数只使用数字0、1，如二制数 11011101(2)，1101 ( 2)通式子 1 23 1 220 2 1 可以十制数13，仿照上面的方法，将二制数 11101 (2)十制数是（）．（ A）29（ B） 25（C） 4（ D） 33【解答】算机中的“二制”， A例 2 察下列序排列的等式：猜想：第n 个等式（ n 正整数）___________________ 。

【解答】（或）例 3 用黑白两种色的正六形地面按如下所示的律，拼成若干个案：（ 1）第四个案中有白色地；（ 2）第n 个案中有白色地.⋯⋯第一个第二个第三个第10 题图【解答】（1） 18；（2）4n2例 4(1)如表 , 方程 1, 方程 2,.方程 3, ⋯ , 是按一定律排列的一列方程, 解方程 1, 将它的解填在表中的空白；(2)若方程a11(a)的解是 x16, x2 10 ，求a、b的.方程是不是(1)中x x b b所 出的一列方程中的一个方程?如果是 , 它是第几个方程 ?(3) 写出 列方程的第n 个方程的解 , 并 所写的解适合第 n 个方程 .序号方程方 程 的 解6 1 x 1, x 21x1x28 1 x 14,x 262x1x310 1 x 15, x 263x1x4⋯⋯⋯【分析】 比 、 分析、 察、 猜想、 、 概括、 等思 方法的考 是此 的独到之.【解答】 (1)6121, 整理 , 得 x 2 7 x 12 0 .解得 x 1 3, x 2 4 .xx 知 ,x 13,x 2 4是原方程的根 .a 1 1,66(2) 将 16,10a 1, 得b2x分 代入1a1xx x b10 10 1 .b 消去 a, 整理 , 得 b 217 b 60 0 , 1 212.解得 b 5,b当 b 1 5 时 ,b 212；当 b 212 时 , a 212.∵ a>b, ∴a12,b5.知 ,a 12,适合分式方程 .b 5所得方程12 x 1 1, 它是 (1) 中所 一列方程中的一个 , 是第 4 个.x5(3) 列方程的第n 个方程2(n2)x1 1 (n ≥2,n 整数 ).x(n 1)它的解 x 1 n2,x 2 2(n1).: 当 x n 2,左 =2( n2) ( n 2) 1 1) 2 1 1 =右 .n 2(n当 x （2n 1） ,左 =2( n 2) 1 n 211 = 右 （ ）2(n 1) (n 1) n 1n2 n 11所以 x 1 n2,x 22(n1). 是方程2(n2)11 的解 .xx (n 1)a11,6 6 b【说明】应该消去未知数a, 而用换元法是徒劳的. 验证一个数是否是方程的根a1 10101. b方法，只需将这个数作为未知数的值分别代入方程的左右两边, 验证左边是否等于右边即可.注意不要直接代入方程.例5 探究规律：如图 3（ 1）1，已知直线m∥n， A、 B 为直线n上的两点， C、 P 为直线m上的两点 .（ 1）请写出图中面积相等的各对三角形：.（ 2）如果 A、B、 C 为三个定点，点P 在m上移动，那么无论P 点移动到任何位置总有：与△ ABC的面积相等；理由是：.C PEm E NAD AO DA B nBC B C M第 26 题图 1图 3（ 2）第 26 题图 3第 26题图 2图 3（1）图 3（ 3）解决问题：如图 3（ 2），五边形 ABCDE是张大爷十年前承包的一块土地的示意图，经过多年开垦荒地，现已变成如图3（ 3）所示的形状，但承包土地与开垦荒地的分界小路（图3（ 3）中折线CDE）还保留着，张大爷想过 E 点修一条直路，直路修好后，要保持直路左边的土地面积与承包时的一样多 . 请你用有关的几何知识，按张大爷的要求设计出修路方案 .（不计分界小路与直路的占地面积）（1）写出设计方案，并在图 3（3）中画出相应的图形；（2）说明方案设计理由 .【解答】探究规律：（ 1）△ ABC和△ ABP, △ AOC和△ BOP, △ CPA和△ CPB;(2)△ ABP.因为平行线间的距离相等，所以无论点P 在 m上移动到任何位置，总有△ABP与△ABC同底等高，因此，它们的面积总相等.解决问题：（ 1）画法如图 .连结 EC, 过点 D 作 DF//EC,交CM于点F,连结EF, EF即为所求直路的位置.（ 2）设 EF 交 CD于点 H,由上面得到的 ，可知：△ ECF △ ECD△ HCF△ EDHS=S , S=S .∴ S五边形 ABCDE五边形 ABCFE=S ,S 五边形 EDCMN = S 四边形 EFMN .AENDBMFC【中考 精 】一、1. 算机是将信息 成二 制数 行 理的，二 制即“逢21”，如 (1101) 2表示二制数，将它 成十 制形式是1231 22 021 1 2013 ，那么将二 制数(1111) 2 成十 制形式是数（）．A 、 8B 、 15 C、 20 D 、 302. 小王利用 算机 了一个 算程序， 入和 出的数据如下表：入⋯ 1 2 3 4 5 ⋯出⋯1 2 3 4 5 ⋯2 5 101726那么，当 入数据是 8 ， 出的数据是（ ）CA 、8B、8C、8D、8616365673. 下面一 按 律排列的数：1,2 ， 4,8 ， 16，⋯⋯，第 2002 个数 是（）．A 、 22002B 、 22002 － 1C 、 22001D 、以上答案不4. 小亮从一列火 的第 m 数起，一直数到第 n （ n ＞ m ），他数 的 数是（）．C（ A ） m ＋ n （ B ） n － m （ C ）n － m － l （D ） n － m ＋15. （ 1）是一个水平 放的小正方体木 ， （ 2）、（ 3）是由 的小正方体木 叠放而成，按照 的 律 叠放下去，至第七个叠放的 形中， 小正方体木 数 是 （）．C（A） 25 （B） 66 （C） 91 （ D） 120(1)(2)(3)二、填空1. 察下列算式：21 222 4238241625322664 2712828256通察，用你所的律写出89的末位数是. 22.古希腊数学家把数 1， 3， 6，10， 15， 21，⋯⋯，叫做三角形数，它有一定的律性，第 24 个三角形数与第22 个三角形数的差.3.你察思考下列算程：∵ 112＝121，∴121＝11；同：∵ 1112＝ 12321，∴12321 ＝111；⋯⋯由此猜想12345678987654321=。

北师大版七年级数学上学期探索与表达规律课后练习题初中数学课堂上大家学习了很多数学知识点，在课下大家要及时进行练习巩固，通过做练习题能够让大家发现自己课堂上没掌握好的知识点，下面为大家带来北师大版七年级数学上学期探索与表达规律课后练习题，希望有助于大家学好初中数学知识。

1. 观察下面三行数：-2，4，-8，16，-32，64 ①0，6，-6，18，-30，66②-1，2，-4，8，-16，32③(1)第①行数按什么规律排列?(2)第②③行数与第①行数有什么关系?(3)取每行数的第十个数，计算这三个数的和.2. 解答题.观察下列各算式：9-1=8，16-4=12，25-9=16，36-16=20.(1)第5个算式是什么?第6个算式是什么?(2)第n个算式是什么?(用n来表示)3. 给出一组式子：32+42=52，52+122=132，72+242=252，92+402=412，112+602=612，(1)请你观察给出的式子，找出一些规律并写出，运用所发现的规律给出第10个式子，并利用计算器验证所得式子的正确性;(2)已知：20032+p2=q2，其中p，q为连续正整数，且q=p+1，用较为简便的方法写出p和q的值，并利用计算器验证它的正确性.4. 两个人做游戏：轮流报数，报出的数不能超过8(也不能是O)，即是1，2，3，4，5，6，7，8中的一个，把两个人报出的数连加起来，谁报数后能使他们报出的数和为88，谁就获胜.如果让你先报数，那么你如何报数才能一定获胜?5. 观察下面三行数：2，-4，8，-16，①-1，2，-4，8，②3，-3，9，-15，③(1)第①行数按什么规律排列?(2)第②③行数与第①行数分别有什么关系?(3)取每行数的第10个数，计算这三个数的和?为大家带来了北师大版七年级数学上学期探索与表达规律课后练习题，希望大家能够养成课后做数学练习题的好习惯，这样能够在做题中加深大家对初中数学知识点的掌握程度。

初中数学北师大版七年级上册探索规律经典题型试题七年级<上>探索规律经典题型及答案参考答案1、 B2、 An3、 C(可列式为，当n=8时，选C) 2n，14、 C(设这三个数为n，n+7，n+7+7，则其和为3n+21，代入验证即可) 225、 2n+1= ，，n，1,n6、78 632n，17、 65个(规律为)118、由(1)可得f(n)=n-1，由(2)可得f()=n，所以f()-f(2009)=2009-n2009 (2009-1)=19、 9(n-1)+n=10n-1 ，nn210、规律为n，,n，，所以a=10，b=99，a+b=109 22n,1n,111、n=1时，火柴根数为:3，即3(1+0) ，n=2时，火柴根数为:9，即3(2+1) ，n=3时，火柴根数为:18，即3(3+2+1) ，…n，1，n，，3，n=n时，火柴根数为:3(n+n-1+…+3+2+1)= ，2所以，当n=20时，代入即得火柴根数为630根 12、 4n+2(1) (2) (3) (4) (5) (6)1 4 9 16 25 362n2200913、(1)a+3b(2)依题意得出:a+3b=18a+(15-1)b=2 ，，，,,a，5,1b解后得 a=12b=2其规律为:12+2(n-1)=2n+10所以第21排有52个位置14、注意:自右至左每隔5厘米染上一个红点，这也相当于自左至右每隔5厘米染上一个红点(因为100可以被5整除~)下面我们来分类讨论:(经过上述注意后，以下所说的距离都是与木棍左端的距离～～) 1、设符合题意的6cm的红点在左，则看看自左至右第一种情况相距4cm 的两个红点的位置:因为25-16= 4，不难得出按照题意截取4cm的木棍的两个关键点在靠左的红点在距左，，端16=6cm处、靠右的红点25=10cm，这样的情况每隔56= 30cm出现一次，共，，，(100-10)/30 +1= 4次，即这种情况有4根。

…… 一、 基础练习
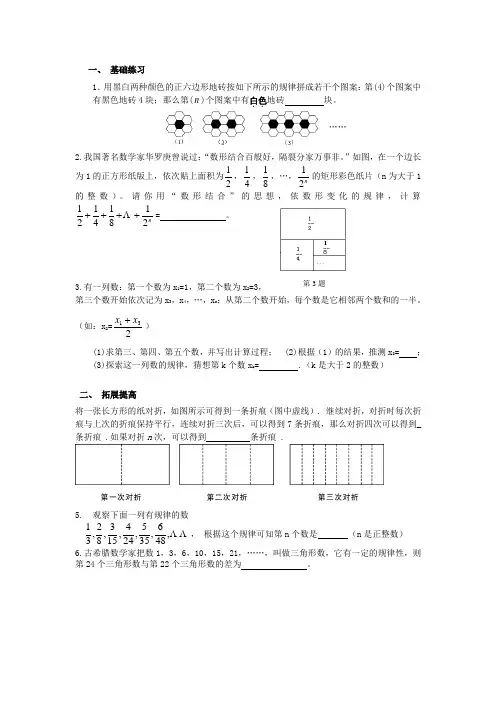
1．用黑白两种颜色的正六边形地砖按如下所示的规律拼成若干个图案：第(4)个图案中
有黑色地砖4块；那么第(n )个图案中有白色．．
地砖 块。

2.我国著名数学家华罗庚曾说过：“数形结合百般好，隔裂分家万事非。

”如图，在一个边长为1的正方形纸版上，依次贴上面积为21，41，81，…，n 2
1的矩形彩色纸片（n 为大于1的整数）。

请你用“数形结合”的思想，依数形变化的规律，计算n 2
1814121++++ = 。

3.有一列数：第一个数为x 1=1，第二个数为x 2=3，
第三个数开始依次记为x 3，x 4，…，x n ；从第二个数开始，每个数是它相邻两个数和的一半。

（如：x 2=2
31x x +） (1)求第三、第四、第五个数，并写出计算过程； (2)根据（1）的结果，推测x 8= ；
(3)探索这一列数的规律，猜想第k 个数x k = .（k 是大于2的整数）
二、 拓展提高
将一张长方形的纸对折，如图所示可得到一条折痕（图中虚线）. 继续对折，对折时每次折
痕与上次的折痕保持平行，连续对折三次后，可以得到7条折痕，那么对折四次可以得到_ 条折痕 .如果对折n 次，可以得到 条折痕 .
5. 观察下面一列有规律的数
,48
6,355,244,153,82,31， 根据这个规律可知第n 个数是 （n 是正整数） 6.古希腊数学家把数1，3，6，10，15，21，……，叫做三角形数，它有一定的规律性，则第24个三角形数与第22个三角形数的差为 。

第3题。

1条2条3条七年级数学（上）探索规律类 问题班级 学号 姓名 成绩一、数字规律类：1、一组按规律排列的数：41，93，167，2513，3621，…… 请你推断第9个数是 ． 2、（2005年山东日照）已知下列等式： ① 13＝12； ② 13＋23＝32； ③ 13＋23＋33＝62； ④ 13＋23＋33＋43＝102 ；…………由此规律知，第⑤个等式是 ． 3、（2005年内蒙古乌兰察布）观察下列各式；①、12+1=1×2 ；②、22+2=2×3；③、32+3=3×4 ；………请把你猜想到的规律用自然数n 表示出来 。

4、（2005年辽宁锦州）观察下面的几个算式：①、1+2+1=4； ②、1+2+3+2+1=9；③、1+2+3+4+3+2+1=16；④、1+2+3+4+5+4+3+2+1=25，……根据你所发现的规律，请你直接写出第n 个式子 5、（2005年江苏宿迁）观察下列一组数的排列：1、2、3、4、3、2、1、2、3、4、3、2、1、…，那么第2005个数是（ ） A ．1 B ． 2 C ．3 D ．4 6、（2005年山东济南市）把数字按如图所示排列起来，从上开始，依次为第一行、第二行、第三行、……，中间用虚线围的一列，从上至下依次为1、5、13、25、……，则第10个数为________。

第1行 1第2行 －2 3第3行 －4 5 －6第4行 7 －8 9 －10第5行 11 －12 13 －14 15 ……………… 7、（05年江苏省金湖实验区）已知一列数：1，―2，3，―4，5，―6，7，… 将这列数排成如上所示的形式：按照上述规律排下去，那么第10行从左边数第5个数等于 ． 二、图形规律类： 8、（2005年云南玉溪）一质点P 从距原点1个单位的A 点处向原点方向跳动，第一次跳动到OA 的中点1A 处，第二次从1A 点跳动到O 1A 的中点2A 处，第三次从2A 点跳动到O 2A 的中点3A 处，如此不断跳动下去，则第n 次跳动后，该质点到原点O 的距离为 。

探索规律班级：__________________________姓名：__________________________作业导航体验从简单的局部的特殊情况出发，去发现一般规律的过程．一、填空题1．在横线上填写适当的数．（1）2、4、6、_____、10、12、…（2）2、3、5、8、12、_________……2．有一列数1，2，3，4，5，6……当按顺序从第2个数到第6个数时共数了_____个数，当按顺序从第m 个数数到第n 个（n ＞m ）数时，共数了_____个数．3．已知31＝3，32＝9，33＝27，34＝81，35＝243，36＝729，37＝2187，38＝6561……推测320的个位数是__________4．下面由火柴杆拼出的一列图形中，第n 个图形由n 个正方形组成，观察发现第四个图形中火柴杆有______根，第n 个图案中有火柴杆______根．图15．观察下列等式：1＝21×1（1＋1） 1＋2＝21×2（2＋1） 1＋2＋3＝21×3（3＋1） ……设n 为正整数，则1＋2＋3＋…＋n ＝__________．6．观察图2，按规律排列的数表，可以知道表中的数n ＝__________．图27．研究下列等式1＝12，1＋3＝4＝22，1＋3＋5＝9＝32，1＋3＋5＋7＝16＝42，1＋3＋5＋7＋9＝25＝52，…当n 为正整数时，1＋3＋5＋7＋…＋（2n －1）＝__________．8．观察下列等式：1×3＝3即3＝22－1，3×5＝15即15＝42－1，5×7＝35即35＝62－1，……，11×13＝143即143＝122－1，…将你猜想到的规律用只含一个字母的式子表示出来__________．二、解答题9．已知4个矿泉水瓶可以换一瓶矿泉水，现有15个矿泉水空瓶若不交钱最多可以喝矿泉水几瓶？10．观察算式：32－1＝8＝8×152－32＝16＝8×272－52＝24＝8×392－72＝32＝8×4你能发现什么规律，请用公式表示．11．问题：你能很快算出952吗？为了解决这个问题，我们考察了3个个位上的数为5的自然数的平方，任意一个个位数是5的自然数可写成10n ＋5即求（10n ＋5）2的值．（n 为自然数），你试分析n ＝1，n ＝2，n ＝3，……这些简单情况，从中探索其规律，并归纳猜想出结论（在下面空格内填上你的探索结果）．①通过计算，探索规律152＝225可写成100×1（1＋1）＋25，252＝625可写成100×2（2＋1）＋25，352＝1225可写成100×3（3＋1）＋25，752＝5625可写成__________,852＝7225可写成__________．②从第①题的结果，归纳、猜想得（10n ＋5）2＝_______．③根据上面的归纳、猜想，请算出952＝_______．12．你能比较两个数19971998和19981997的大小吗？为解决这个问题，我们先写出它的一般形式即比较n n ＋1和（n ＋1）n 的大小（n 是自然数），然后，我们分析n ＝1，n ＝2，n ＝3，……从中发现规律，经归纳、猜想得出结论．①通过计算比较下列各组数中两个数的大小（在空格中填写“＞”“＝”“＜”号）：12______21，23______32，34______43，45______54，56______65，…②从第①题的结果经过归纳，可以猜想出n n ＋1和（n ＋1）n 的大小关系是______．③根据上面的归纳猜想得到一般结论，试比较下列两个数的大小19981999____19991998．13．有一堆木料共20层，从上往下数第一层一根，第二层两根，第三层三根……，第二十层二十根． ①用简便方法求出这堆木料的总根数，答共有_____根；②用类似的方法求值：1＋2＋3＋…＋100＝_____③试求1＋2＋3＋…＋n 的值．参考答案一、1．（1）8 （2）17 2．5 n －m ＋13．1 4．13 3n ＋1 5．21n （n ＋1） 6．4 7．n 2 8．（2n －1）（2n ＋1）＝（2n ）2－1二、9．4瓶10．（2n ＋1）2－（2n －1）2＝8n11．①100×7（7＋1）＋25 100×8（8＋1）＋25②100×n （n ＋1）＋25③100×9（9＋1）＋25＝902512．①＜ ＜ ＞ ＞ ＞②当n ＞2时，n n ＋1＞（n ＋1）n③＞n)1n(13．①210②5050③2。

探索规律一、选择题1.小王利用计算机设计了一个计算程序，输入和输出的数据如下表：输入 … 1 2 3 4 5 … 输出…«SkipRecord If...» «SkipRecord If...» «SkipRecord If...» «SkipRecord If...» «SkipRecord If...»…那么，当输入数据是8时，输出的数据是（ ）A 、«Skip Record If...»B 、«Skip Record If...»C 、«Skip Record If...»D 、«Skip Record If...»2.下面一组按规律排列的数：1,2，4,8，16，……，第2002个数应是（ 2、2001 ）．A 、«Skip Record If...»B 、«Skip Record If...»－1C 、«SkipRecord If...»D 、以上答案不对3.小亮从一列火车的第m 节车厢数起，一直数到第n 节车厢（n ＞m ），他数过的车厢节数是（ ）．C（A ）m ＋n （B ）n －m （C ）n －m －l （D ）n －m ＋14.图（1）是一个水平摆放的小正方体木块，图（2）、（3）是由这样的小正方体木块叠放而成，按照这样的规律继续叠放下去，至第七个叠放的图形中，小正方体木块总数应是（ ）．C （A ）25 （B ）66 （C ） 91（D ）120二、填空题1、用黑白两种颜色的正六边形地面砖按如下所示的规律，拼成若干个图案： （1）第四个图案中有白色地砖 块；（2）第n 个图案中有白色地砖 块.(1)(2)(3)……第10题图第三个第二个第一个2、观察下列算式：«Skip Record If...» «Skip Record If...» «Skip Record If...» «Skip Record If...» «Skip Record If...» «Skip Record If...» «Skip Record If...» «Skip Record If...» 通过观察，用你所发现的规律写出«Skip Record If...»的末位数是 . 23、古希腊数学家把数1，3，6，10，15，21，……，叫做三角形数，它有一定的规律性，则第24个三角形数与第22个三角形数的差为 .4、请你观察思考下列计算过程：∵«Skip Record If...»＝121，∴«Skip Record If...»＝11；同样：∵«Skip Record If...»＝12321，∴«Skip Record If...»＝111；……由此猜想«Skip Record If...»= 。

北师版七年级上册第三章整式及其加减规律探索 专项训练一、填空题1．已知：一组数1，3，5，7，9，…，按此规律，则第n 个数是___________． 2．已知：一组数1，4，7，10，13，…，按此规律，则第n 个数是__________．3．观察下列一组数：32，1，710，1917，1126，…，它们是按一定规律排列的，那么这组数的第n 个数是____________．(n 为正整数)4．按一定规律排列的一列数：21，22，23，25，28，213，221，….若x ，y ，z 表示这列数中的连续三个数，猜想x ，y ，z 满足的关系式是______________．5．观察一列数：a 1＝3，a 2＝9，a 3＝27，a 4＝81……则a 6＝________，a n ＝________． 6．观察下列数表：请猜想第n 行第n 列交叉点上的数应为___________．7．小李用围棋子排成下列一组有规律的图案，其中第1个图案有1枚棋子，第2个图案有3枚棋子，第3个图案有4枚棋子，第4个图案有6枚棋子……那么第9个图案的棋子数是________枚．8．观察下列一组数：－1，12，－13，14，－15，16……则第7个数是_______，第8个数是_______，第n 个数是 ．9. 找出下列各图形中数的规律，依此判断，a的值为________．10．观察下列式子：1×3＋1＝22；7×9＋1＝82；25×27＋1＝262；79×81＋1＝802；……可猜想第n个式子为_____________________________．11. 如图，该数表是由1开始的连续自然数组成，观察规律并完成下列各题．(1)表中第8行的最后一个数是_______，它是自然数________的平方，第8行共有________个数；(2)用含n的代数式表示：第n行的第一个数是____________，最后一个数是__________，第n行共有_____________个数．12．观察下列等式：9×0＋1＝1；9×1＋2＝11；9×2＋3＝21；9×3＋4＝31；9×4＋5＝41；……猜想第n(n为正整数)个等式应为___________________________．13. 观察下列式子：1×3＋1＝22；7×9＋1＝82；25×27＋1＝262；79×81＋1＝802；……可猜想第2019个式子为____________________________．14．观察下列一组图形：它们是按照一定规律排列的，依照此规律，第n个图形共有_______________个.15．按如下规律摆放三角形：(1)第④堆三角形的个数为___________；(2)第○n堆三角形的个数为__________二、选择题16. 我们将如图所示的两种排列形式的点的个数分别称作“三角形数”(如1，3，6，10，…)和“正方形数”(如1，4，9，16，…)，在小于200的数中，设最大的“三角形数”为m，最大的“正方形数”为n，则m＋n的值为( )A．33 B．301C．386 D．57117. 把三角形按如图所示的规律拼图案，其中第①个图案中有4个三角形，第②个图案中有6个角形第③个图案中有8个三角形，…，按此规律排列下去，则第⑦个图案中三角形的个数为( )A．12 B．14C．16 D．1818. 观察下列一组图形，其中图形①中共有2颗星，图形②中共有6颗星，图形③中共有11颗星，图形④中共有17颗星，…，按此规律，图形⑧中星星的颗数是( )A．43颗B．45颗C．51颗D．53颗19．如图用棋子摆出下列一组“口”字，按照这种方法摆下去，则摆第n个“口”需用棋子( ) A．4n枚B．(4n－4)枚C．(4n＋4)枚D．n2枚20. 用大小相等的小正方形按一定规律拼成下列图形，则第n个图形中小正方形的个数是( )A．(2n＋1)个B．(n2－1)个C．(n2＋2n)个D．(5n－2)个21．某校组织若干师生到活动基地进行社会实践活动．若学校租用45座的客车x辆，则余下20人无座位；若租用60座的客车则可少租用2辆，且最后一辆还没坐满，则乘坐最后一辆60座客车的人数是( )A．200－60xB．140－15xC．200－15xD．140－60x三、解答题22．一串数字的排列规律是：第一个数是20，从第二个数起，每一个数比前一个数小8.(1)第10个数是多少？(2)第n个数是多少？(3)第几个数是－60?23．仔细观察下列三组数：第一组：1，4，9，16，25……第二组：1，8，27，64，125……第三组：－2，－8，－18，－32，－50……(1)写出每组的第6个数各是多少？(2)第二组的第100个数是第一组的第100个数的多少倍？(3)取每组数的第n个数，计算这三个数的和．24．观察图中的棋子：(1)按照这样的规律摆下去，第4个图形中的棋子个数是多少？(2)用含n的式子表示第n个图形的棋子个数．25．观察下列算式：22－02＝4＝4×1，42－22＝12＝3×4，62－42＝20＝5×4，82－62＝28＝7×4，….(1)按照此规律，写出第五个等式；(2)按照此规律，写出第n个等式；参考答案 一、填空题 1. 2n －1 2. 3n －2 3. 2n+1n 2+14. xy ＝z5. 729，3n6. 2n －17. 138. －17，18，(－1)n 1n9. 22610. (3n －2)×3n ＋1＝(3n －1)2 11. (1)64，8，15 (2)(n －1)2＋1，2n －1。

3.6 探索规律一、选择题1.如图,某人沿着边长为40m 的正方形,按A →B →C →D →A →……方向,甲从A 以65米/分的速度,乙从B 以72米/分的速度行走,当乙第一次追上甲时在正方形的(• )A.AB 边上B.DA 边上C.BC 边上D.CD 边上 2.有以下两下数串:1,3,5,7,……1991,1993,1995,1997,1999和1,4,7,10•……1990,1993,1996,1999,同时出现在这两个数串中的数的个数共有( )个.A.333B.334 D.335 D.3363.百货大楼进了一批花布,出售时要在进价(进货价格)的基础上加一定的利润,其数量x 与售价y 如下表下列用数量x 表示售价y 的关系中,正确的是( )A.y=8x+0.3B.y=(8+0.3)x;C.y=8+0.3xD.y=8+0.3+x4.当n 非常大时,314n n的值接近于什么数( ) A.34 B.0 C.43 D.-14二、填空题5.从2开始,将连续的偶数相加,其和的情况如下:2=1×2,2+4=6=2×3,2+•4+•6=12=3×4,2+4+6+8=20=4×5,……2+4+6+…+24=______=______×______,将从2开始n 个连续的偶数相加,试写出用n 表示的代数式2+4+6+…+2n=________.6.研究下列算式,你可以发现一定的规律:1×3+1=4=22,2×4+1=9=33,3×5+1=16=42,4×6+1=25=52•……请你将找出的规律用代数式表示出来:___________.7.观察下列等式:9-1=8,16-4=12,25-9=16,36-16=20,49-25=24…,•这些等式反映出自然数间某种规律,设n 表示自然数,用关于n 的等式表示出来__________. 8.观察下列各式,你会发现什么规律: 3×5=15,而15=42-1 5×7=35,而35=62-1 ……乙甲DCB A11×13=143,而143=122-1……将你观察到的规律用只含一个字母的式子表示出来__________.三、解答题:9.用火柴棒按下图中的方式搭图形:①②③④⑤(2)搭第n个图形需多少根火柴棒.(3)搭第n个图形需要多少根火柴棒.10.比较下面两列算式结果的大小(在横线上选填“>”、“<”、“＝”〉52+72________2×5×7(-9)2+42______2×(-9)×4(-6)2+(-8)2_______2×(-6)×(-8)32+32_____2×3×3……通过观察归纳,写出能反映出怎样的一般规律.11.(1)通过计算比较下列各组数中两个数的大小,在空格中填写“>”、•“<”、“＝”.①12_____21 , ②23_____32 , ③34______43 , ④45_____54(2)从第(1)题的结果通过归纳可以猜想n n+1与(n+1)n的大小关系,比较20032004•与20042003的大小.参考答案一、1.B 2.B 3.B 4.A二、5.156,12×13,n(n+1)6.(n-1)(n+1)+1=n27.(n+1)2-(n-1)2=4n (n≥2) •8.(2n-1)(2n+1)=(2n)2-1 (n≥2)三、(2)搭第13个图形所用火柴楼是5×13-12=53(根)(3)搭第几个图形所用的火柴棒是5a-(n-1)=5n-n+1=4n+110.>;>;>;=;通过观察归纳,反映规律:a,b为任意有理数,a2+b2≥2ab11.(1)①< ②< ③< ④<; (2)n n+1<(n+1)n ; (3)20032004<20042003。

七上规律题练习1、观察下面的一列单项式：﹣x 、2x2、﹣4x3、8x4、﹣16x5、…根据其中的规律，得出的第10个单项式是（ ） A ． ﹣29x 10B ．29x 10 C ． ﹣29x 9D ． 29x 92、已知整数a 1，a 2，a 3，a 4，…满足下列条件：a 1=0，a 2=－|a 1+1|，a 3=－|a 2+2|，a 4=－|a 3+3|，…，依此类推，则a 2012的值为（ ）。

A 、－1005B 、－1006 D 、－1007 D 、－20123、若规定“!”是一种数学运算符号，且1！=1，2！=2×1=2，3！=3×2×1=6，4！=4×3×2×1=24，....则的值为（）。

A. B.99! C.9900 D.2!4、若规定，则的值为 .5、已知 434434,323323,212212+=⨯+=⨯+=⨯,若b a b ab a 、(1010+=⨯都是正整数),则b a += .7、观察下列图形：它们是按一定规律排列的，依照此规律，第16个图形共有 个★．8、如图是一个数值转换机的示意图，若输入的值为3，的值为－2，则输出的结果为 ． 9、观察下列单项式：－2x ，22x 2，－23x 3，24x 4，…，－219x 19，你能写出第n 个单项式吗？并写出第2013个单项式。

为解决这个问题，我们不妨从系数和次数两个方面入手进行探究，从中发现规律，经过归纳，猜想出结论。

!98!1004950x10、观察下列各式：332211129492344+==⨯⨯=⨯⨯3332211123369163444++==⨯⨯=⨯⨯33332211123410016254544+++==⨯⨯=⨯⨯… … …（1）计算：33333123410++++⋅⋅⋅+的值 （2）试猜想333331234n ++++⋅⋅⋅+的值11、如图，图1是个正五边形，分别连接这个正五边形各边中点得到图2，再分别连接图2小正五边形各边中点得到图3：图１ 图2 图3(1)填写下表：(2)按上面方法继续连下去，第n 个图中有多少个三角形？ (3)能否分出246个三角形？简述你的理由。

试题汇编——找规律1、如图所示，观察小圆圈的摆放规律，第一个图中有5个小圆圈，第二个图中有8个小圆圈，第100个图中有__________个小圆圈．（1） （2） （3）2、 找规律．下列图中有大小不同的菱形，第1幅图中有1个菱形，第2幅图中有3个菱形，第3幅图中有5个菱形，则第4幅图中有 个菱形,第n 幅图中有 个菱形．3、用同样大小的黑色棋子按下图所示的方式摆图形，按照这样的规律摆下去，则第n 个图形需棋子 枚（用含n 的代数式表示）.4、观察表一，寻找规律．表二、表三、表四分别是从表一中截取的一部分，其中a 、b 、c 的值分别为______________．5、如图①是一块瓷砖的图案，用这种瓷砖来铺设地面．如果铺成一个22⨯的正方形图案（如图②），其中完整的圆共有5个，如果铺成一个33⨯的正方形1 2 3 n … … 第1个图 第2个图 第3个图…图案（如图③），其中完整的圆共有13个，如果铺成一个44⨯的正方形图案（如图④），其中完整的圆共有25个．若这样铺成一个1010⨯的正方形图案， 则其中完整的圆共有 个．6、 如下图,用同样大小的黑、白两种颜色的棋子摆设如下图所示的正方形图案，则第n 个图案需要用白色棋子 枚（用含有n 的代数式表示，并写成最简形式）.○ ○ ○ ○ ○ ○ ○ ○ ○○ ○ ○ ○ ● ● ○ ○ ● ● ● ○○ ● ○ ○ ● ● ○ ○ ● ● ● ○○ ○ ○ ○ ○ ○ ○ ○ ● ● ● ○○ ○ ○ ○ ○7、用火柴棒按下图中的方式搭图形，按照这种方式搭下去，搭第334个图形 需 根火柴棒。

8、将正整数按如图5所示的规律排列下去，若有序实数对（n ，m ）表示第n 排，从左到右第m 个数，如（4，2）表示实数9，则表示实数17的有序实数对是 ．9、如图 2 ，用n 表示等边三角形边上的小圆圈，f(n)表示这个三角形中小圆圈的总数，那么f(n)和n 的关系是第一排 第二排 第三排 第四排 6 ┅┅ 10 9 87 32 15 410、观察图4的三角形数阵，则第50行的最后一个数是 （ ）1-2 3-4 5 -67 -8 9 -10。

习地址：佛山市南海区桂城南海大道丽雅苑中区会所2楼（南海体育馆对面） 1 鼎吉教育吉红勇老师编辑七年级数学上册§3.6《探索规律》同步练习【知识要点】1、探索规律就是一种观察、归纳、猜想、验证的过程.是一个创新意识的培养过程， 体现了从特殊到一般的数学思想2、探索规律主要是以下题型：（1）棋牌规律 （2）图形规律（重点） （3）剪纸规律 （4）算式规律（重点）【典例精析】一、棋牌规律例1．（2004河北）小明背对小亮，让小亮按下列四个步骤操作： 第一步 分发左、中、右三堆牌，每堆牌不少于两张，且各堆牌的张数相同；第二步 从左边一堆拿出两张，放入中间一堆； 第三步 从右边一堆拿出一张，放入中间一堆；第四步 左边一堆有几张牌，就从中间一堆拿几张牌放入左边一堆.这时，小明准确说出了中间一堆牌现有的张数.你认为中间一堆牌的张数是 .二、图形规律例2．（2004泸州）把正方体摆放成如图（5）的形状，若从上至下依次为第1层，第2层，第3层，……，则第n 层有 个正方体. 三、算式规律例3． 观察下列顺序排列的等式：9×0＋1＝1， 9×1＋2＝11， 9×2＋3＝21， 9×3＋4＝31， 9×4＋5＝41，…… ．猜想：第n 个等式（n 为正整数）应为________________ 四、剪纸规律例4、（2004年浙江衢州）如图（11），将一张正方形纸片剪成四个小正方形，然后将其中的一个正方形再剪成四个小正方形，再将其中的一个正方形剪成四个小正方形，如此继续下去，……，根据以上操作方法，请你填写下表： 五、对称规律例5、（2004年山东日照）在日常生活中，你会注意到有一些含有特殊数学规律的车牌号码，如：鲁L80808 、鲁L22222、鲁L12321等，这些牌照中的五个数字都是关于中间的一个数字“对称”的，给以对称的美的感受，我们不妨把这样的牌照叫做“数字对称”牌照。

智立方教育初一(上)数学试题分类汇编——找规律1、如图所示，观察小圆圈的摆放规律，第一个图中有5个小圆圈，第二个图中有8个小圆圈，第100个图中有__________个小圆圈．（1） （2） （3）2、 找规律．下列图中有大小不同的菱形，第1幅图中有1个菱形，第2幅图中有3个菱形，第3幅图中有5个菱形，则第4幅图中有 个菱形,第n 幅图中有 个菱形．3、用同样大小的黑色棋子按下图所示的方式摆图形，按照这样的规律摆下去，则第n 个图形需棋子 枚（用含n 的代数式表示）.4、观察表一，寻找规律．表二、表三、表四分别是从表一中截取的一部分，其中a 、b 、c 的值分别为______________．5、如图①是一块瓷砖的图案，用这种瓷砖来铺设地面．如果铺成一个22⨯的正方形图案（如图②），其中完整的圆共有5个，如果铺成一个33⨯的正方形图案（如图③），其中完整的圆共有13个，如果铺成一个44⨯的正方形图案（如图④），其中完整的圆共有25个．若这样铺成一个1010⨯的正方形图案， 则其中完整的圆共有 个．1 2 3n … … 第1个图第2个图第3个图 …6、 如下图,用同样大小的黑、白两种颜色的棋子摆设如下图所示的正方形图案，则第n 个图案需要用白色棋子 枚（用含有n 的代数式表示，并写成最简形式）.○ ○ ○ ○ ○ ○ ○ ○ ○○ ○ ○ ○ ● ● ○ ○ ● ● ● ○○ ● ○ ○ ● ● ○ ○ ● ● ● ○○ ○ ○ ○ ○ ○ ○ ○ ● ● ● ○○ ○ ○ ○ ○7、用火柴棒按下图中的方式搭图形，按照这种方式搭下去，搭第334个图形需 根火柴棒。

8、将正整数按如图5所示的规律排列下去，若有序实数对（n ，m ）表示第n 排，从左到右第m 个数，如（4，2）表示实数9，则表示实数17的有序实数对是 ．9、如图 ２ ，用n 表示等边三角形边上的小圆圈，f(n)表示这个三角形中小圆圈的总数，那么f(n)和n 的关系是10、观察图4的三角形数阵，则第50行的最后一个数是 （ ）1-2 3-4 5 -67 -8 9 -10。

第04讲探索与表达规律(6类热点题型讲练)1.探索运用符号表示数字规律和图形规律的方法.2.提高观察图形、探索规律的能力，培养创新意识.知识点01规律探究常见的数字规律规律总结数列形式21n -1，3，5，7，9，···，21n -2n 2，4，6，8，10，···，2n 13+n 4，7，10，13，16，···，13+n 13-n 2，5，8，11，14，···，13-n n 22，4，8，16，32，···，n 212+n 3，5，9，17，33，···，12+n 21n +2，5，10，17，26，···，21n +21n -0，3，8，15，24，···，21n -(1)n x -x -，x +，x -，x +，x -，x +，···，(1)n x-1(1)n x+-x +，x -，x +，x -，x +，x -，···，1(1)n x+-(1)2n n +1，3，6，10，15，21，···，(1)2n n +斐波那契数列1，1，2，3，5，8，13，…，从第三个数开始每个数等于与它相邻的前两个数之和知识点02规律探究方法总结1.规律探究的核心是找出每个数与对应的位次（即n ）之间的关系；2.若数列为分数数列，则分子分母分开找规律；3.若数列是正负交替排列，则在答案前加上n )1(-；若数列是负正交替排列，则在答案前加上1)1(+-n ；4.若是选择题，则可以用代值法，再利用排除法选出正确答案即可.知识点03高斯求和定理2)1(2)(14321nn n n ⋅+=⨯+=+-+⋅⋅⋅++++项数末项首项.题型01数字类规律探索之排列问题【典例1】（2023·浙江衢州·校考一模）观察下列数据：0，3，8，15，24，…，它们是按一定规律排列的，依照此规律，第201个数据是（）A ．40400B ．40040C ．4040D ．404【变式1】（2022春·黑龙江哈尔滨·六年级校考期中）一组数据x ，23x -，35x ，47x -，59x …请按这种规律写出第十个数是．【变式2】（2022秋·浙江金华·七年级校考期中）从3开始的连续奇数按右图的规律排列，其余位置数字均为0．（1）第5行第10列的数字是．（2）数字2023在图中的第行，第列．题型02数字类规律探索之末尾数字问题【典例2】（2022秋·江苏连云港·七年级校考阶段练习）观察下列算式：031=，133=，239=，3327=，4381=，53243=，63729=，732187=…归纳各计算结果中个位数字的规律，可得20033的个位数字是（）A ．1B ．3C ．9D ．7【变式1】（2023春·江苏南京·七年级校考阶段练习）观察下列算式：①2(1)(1)1x x x -+=-；②23(1)(1)1x x x x -++=-；③324(1)(1)1x x x x x -+++=-寻找规律，并判断(2011)(2017)222221++⋯+++的值的末位数字为（）A ．1B ．3C ．5D ．7【变式2】（2023春·江苏泰州·七年级统考期中）发现规律解决问题是常见解题策略之一．已知数5555551234529a =++++++ ，则这个数a 的个位数为（）A ．3B ．4C ．5D ．6【变式3】（2023春·江苏连云港·七年级统考期末）生物学中，描述、解释和预测种群数量的变化，常常需要建立数学模型．在营养和生存空间没有限制的情况下，某种细胞可通过分裂来繁殖后代，我们就用数学模型2n 来表示，即：122=，224=，328=，4216=，5232=，……，请你推算123452023222222+++++⋅⋅⋅⋅⋅⋅+的个位数字是（）A ．8B ．6C ．4D ．2题型03数字类规律探索之新运算问题【典例3】（2022·湖南株洲·统考二模）定义一种关于整数n 的“F ”运算：（1）当n 是奇数时，结果为35n +；（2）当n 是偶数时，结果是2k n （其中k 是使2kn是奇数的正整数），并且运算重复进行．例如：取58n =，第一次经F 运算是29，第二次经F 运算是92，第三次经F 运算是23，第四次经F 运算是74，……；若9n =，则第2020次运算结果是（）A ．1B ．2C ．7D ．8【变式1】（2022秋·江苏扬州·七年级校考阶段练习）a 是不为2的有理数，我们把22a-称为a 的“哈利数”．如：3的“哈利数”是2223=--，2-的“哈利数”是()21222=--，已知14a =，2a 是1a 的“哈利数”，3a 是2a 的“哈利数”，4a 是3a 的“哈利数”，．．．，依此类推，则2022a =（）A ．4B ．1-C ．23D ．32【变式2】（2023秋·全国·七年级专题练习）已知整数1a ，2a ，3a ，4a ，……满足下列条件：10a =，211a a =-+，321a a =-+，431a a =-+…，以此类推，则6a 的值为，2022a 的值为题型04数字类规律探索之等式问题【典例4】（2022秋·江西九江·七年级统考期中）观察下面的变形规律：111122=-⨯；1112323=-⨯；1113434=-⨯；解答下面的问题：(1)若n 为正整数，请你猜想()11n n =+______；(2)计算111112233420222023+++⋯⋯+⨯⨯⨯⨯．(3)计算；111124466820202022+++⋯⋯+⨯⨯⨯⨯．【变式1】（2022秋·湖南永州·七年级校考期中）观察算式：()()()132153174131351357.,222,+⨯+⨯+⨯+=++=+++=按规律填空：135799+++++=．【变式2】（2023春·安徽合肥·七年级校考期末）观察算式：①213142⨯+==；②224193⨯+==；③2351164⨯+==；④2461255⨯+==；⋯，根据你发现的规律解决下列问题：(1)写出第5个算式：______；(2)写出第n 个算式：______；(3)计算：111111111324351820⎛⎫⎛⎫⎛⎫⎛⎫+⨯++⨯⨯+ ⎪ ⎪⎪ ⎪⨯⨯⨯⨯⎝⎭⎝⎭⎝⎭⎝⎭．题型05图形类规律探索之数字问题【典例5】（2022秋·湖北黄冈·七年级校考阶段练习）如图，根据图形中数的规律，可推断出a 的值为（）A ．128B ．216C ．226D ．240【变式1】（2023春·贵州毕节·七年级统考期末）根据图中数字的规律，若第n 个图中A B C D ++-的值为196，则n =（）A ．12B ．13C ．14D ．15【变式2】（2022秋·河南周口·七年级校考期中）如图所示，下列各三角形中的三个数之间均具有相同的规律，根据此规律，则第n （n 为正整数）个三角形中，用n 表示y 的式子为（）A ．21n +B ．2n n +C ．12n n ++D ．21n n ++题型06图形类规律探索之数量问题【典例6】（2023·江苏·七年级假期作业）用大小一样的黑白两种颜色的小正方形纸片，按如图的规律摆放：(1)第5个图案有张黑色小正方形纸片；(2)第n 个图案有张黑色小正方形纸片；(3)第几个图案中白色纸片和黑色纸片共有81张？【变式1】（2023秋·全国·七年级专题练习）如图，用棋子摆方阵，那么，图⑥要摆枚棋子，图n 要摆枚棋子．【变式2】（2023·安徽淮北·淮北市第二中学校考二模）如图，利用黑白两种颜色的五边形组成的图案，根据图案组成的规律回答下列问题：(1)图案④中黑色五边形有______个，白色五边形有______个；(2)图案n中黑色五边形有______个，白色五边形有______个；（用含n的式子表示）(3)图案n中的白色五边形可能为2023个吗？若可能，请求出n的值；若不可能，请说明理由．1．（2023秋·全国·七年级专题练习）观察下列各单项式：234562481632a a a a a a ---，，，，，，…，根据你发现的规律，第10个单项式是（）A ．9102a -B ．9102a C ．11002a D ．10102a -2．（2023秋·全国·七年级专题练习）一列数1a ，2a ，3a …n a ，其中11a =-，2111a a =-，3211a a =-，…，11n na a =-，则1232020a a a a ⨯⨯⨯⨯= （）A ．1-B ．1C ．2020D ．2020-3．（2023春·河南信阳·七年级校联考阶段练习）如图，用棋子摆出下列一组图形，如果按照这种规律摆下去，那么第10个图形里棋子的个数为（）A ．72B ．66C ．56D ．784．（2023春·云南临沧·七年级统考期末）如图，用字母“C ”、“H ”按一定规律拼成图案，其中第1个图案中有4个H ，第2个图案中有6个H ，第3个图案中有8个H ，……，按此规律排列下去，第2023个图案中字母H 的个数为()A ．4044B ．4046C ．6069D ．40485．（2023春·福建宁德·七年级校联考期中）我国宋代数学文杨辉所著《详解九章算法》中记载了用如图所示的一角形解释了二项和的乘方展开式中的系数规律，我们把这种数字三角形叫做“杨辉三角”．请你利用杨辉三角，计算()6a b -的展开式中，含3b 项的系数是（）()0a b +=1…………1()1a b +=a b +…………11()2a b +=222a ab b ++…………121()3a b +=322333a a b ab b +++ (1331)()4a b +=++++432234a 4a b 6a b 4ab b (14641)A ．15-B ．15C ．20-D ．20【答案】C【分析】根据图中规律，可得()2a b +的展开式中含3b 项的系数，再根据()6a b -的展开式中，系数的绝对值与()2a b +的展开式中的系数相同，符号从左往后为奇数项为正，偶数项为负．【详解】解：由题意可知，下排每个数等于上方两个数字的绝对值之和，∴5()a b +的展开式系数从左往右分别是1,5,10,10,5,1，6()a b ∴+的展开式系数从左往右分别是1,6,15,20,15,6,1，根据图中，可知()6a b -含有3b 项的项为从左往右第四项，且符号为负，故()6a b -的展开式中，含3b 项的系数是20-，故选：C ．【点睛】本题考查了数字变化规律，通过观察、分析、归纳发现其中规律，并应用发现的规律是解题的关键．6．（2022秋·四川南充·七年级校考期中）正整数按图中的规律排列．由图知，数字6在第二行，第三列，请写出数字2021在第行，第列．7．（2023春·山东泰安·六年级校考期中）观察下列各式，探索规律：21321⨯=-；23541⨯=-；25761⨯=-；27981⨯=-；2911101⨯=-；用含正整数n 的等式表示你所发现的规律为．8．（2023春·黑龙江绥化·七年级校考期末）观察下列算式：133=，239=，3327=，4381=，53243=，⋯，根据上述算式中的规律，你认为20233的末位数字是．9．（2023春·河北石家庄·七年级行唐一中校考开学考试）观察下列图形的构成规律，按此规律，第6个图形中棋子的个数为个，第n 个图形中棋子的个数为个．10．（2022秋·江苏宿迁·七年级校考阶段练习）已知整数1234a a a a ⋅⋅⋅、、、、满足下列条件：11a =-，212a a =-+，323a a =-+，434a a =-+，…，11n n a a n +=-++（n 为正整数）依此类推，则2025a 的值为．11．（2022春·黑龙江哈尔滨·六年级哈尔滨市第十七中学校校考阶段练习）观察下列三行数：2-，4，8-，16，32-，64，……0，6，6-，18，30-，66， (1)2-，1，2-，4，8-，16……(1)第①行数第七个数是128-，那么第二行数第七个数是_____，第三行第七个数是_____．(2)列式计算：取每行的第9个数，求这三个数的和．12．（2023春·云南昭通·七年级统考期中）小明计算：2399100122222++++++L 的过程如下：解：令2399100122222S =++++++①L 则23100101222222S =+++++ ②②-①得10121S =-∴239910010112222221++++++=-L 请参照小明的方法，计算：2320222023155555++++++L ．13．（2023春·安徽阜阳·七年级校考阶段练习）观察下列图形，完成下列问题．(1)数一数，完成下列表格．直线的条数2345交点的个数(2)若有n 条直线相交，则最多有交点__________个．（用含n 的代数式表示）14．（2022秋·江苏连云港·七年级校考阶段练习）观察下列各式：322111124==⨯⨯，33221129234+==⨯⨯，33322112336344++==⨯⨯，33332211234100454+++==⨯⨯L 回答下面的问题：(1)333331234100+++++=（写出算式即可）；(2)计算33333312341920++++++ 的值；(3)计算333311121920++++ 的值．15．（2022秋·江苏宿迁·七年级校考阶段练习）探索规律：观察下面※由组成的图案和算式，解答问题：21342+==213593++==21357164+++==213579255++++==(1)请猜想135719++++⋅⋅⋅+=_________；(2)请猜想()135721n ++++⋅⋅⋅+-=_________；(3)请用上述规律计算：616365199+++⋅⋅⋅+的值．16．（2023秋·浙江·七年级专题练习）找规律，完成下列各题：(1)如图①，把正方形看作1，1111244+=-=．(2)如图②，把正方形看作1，111112488++=-=．(3)如图③，把正方形看作1，1111124816+++=-=．(4)计算：11111 2481632++++=．(5)计算：111111111 248163264128256512++++++++=．17．（2023春·安徽·九年级专题练习）用若干个“○”与“▲”按如图方式进行拼图：(1)观察图形，寻找规律，并将下面的表格填写完整：图1图2图3图4○的个数3921______▲的个数1410______(2)根据你所观察到的规律，分别写出图n中“○”与“▲”的个数（用含n的代数式表示）．18．（2023·河北秦皇岛·统考一模）为迎接七一建党节，某社区党委在广场上设计了一座三角形展台，需在它的每条边上摆放上相等盆数的鲜花进行装饰．若每条边上摆放两盆鲜花，共需要3盆鲜花；若每条边上摆放3盆鲜花，共需要6盆鲜花；……，按此要求摆放下去（如图所示，每个小圆圈表示一盆鲜花）．(1)填写下表：每条边上摆放的盆数（n）23456…需要的鲜花总盆数（y）369__________…(2)写出需要的鲜花总盆数y与n之间的关系式：__________(3)能否用2023盆鲜花作出符合要求的摆放？如果能，请计算出每条边上应摆放的盆数；如果不能，请说明理由．。

3.5 探索与表达规律1.(8分)如图是用棋子摆成的“T”字图案.从图案中可以看出,第一个“T”字图案需要5枚棋子,第二个“T”字图案需要8枚棋子,第三个“T”字图案需要11枚棋子.(1)照此规律,摆成第四个图案需要几枚棋子?(2)摆成第n个图案需要几枚棋子?(3)摆成第2014个图案需要几枚棋子?2.(8分)有规律排列的一列数:2,4,6,8,10,12,…它的每一项可用式子2n(n是正整数)来表示.有规律排列的一列数:1,-2,3,-4,5,-6,7,-8,…(1)它的每一项你认为可用怎样的式子来表示?(2)它的第100个数是多少?(3)2013是不是这列数中的数?如果是,是其中的第几个数?3.(10分)观察下列等式:12×231=132×21,13×341=143×31,23×352=253×32,34×473=374×43,62×286=682×26,…以上每个等式中两边数字是分别对称的,且每个等式中组成两位数与三位数的数字之间具有相同规律,我们称这类等式为“数字对称等式”.(1)根据上述各式反映的规律填空,使式子称为“数字对称等式”:①52×=×25;②×396=693×.(2)设这类等式左边两位数的十位数字为a,个位数字为b,且2≤a+b≤9,写出表示“数字对称等式”一般规律的式子(含a,b且ab≠0).参考答案与解析1.【解析】(1)9+5=14(枚).故摆成第四个图案需要14枚棋子.(2)因为第①个图案有5枚棋子,第②个图案有(5+3×1)枚棋子,第③个图案有(5+3×2)枚棋子,依此规律可得第n个图案需5+3×(n-1)=5+3n-3=(3n+2)枚棋子.(3)3×2014+2=6044(枚),即第2014个图案需6044枚棋子.2.【解析】(1)它的每一项可以用式子(-1)n+1n(n是正整数)表示.(2)它的第100个数是(-1)100+1×100=-100.(3)当n=2013时,(-1)2013+1×2013=2013,所以2013是其中的第2013个数.3.【解析】(1)①因为5+2=7,所以左边的三位数是275,右边的三位数是572,所以52×275=572×25.②因为左边的三位数是396,所以左边的两位数是63,右边的两位数是36,63×396=693×36.(2)因为左边两位数的十位数字为a,个位数字为b,所以左边的两位数是10a+b,三位数是100b+10(a+b)+a,右边的两位数是10b+a,三位数是100a+10(a+b)+b,所以一般规律的式子为:(10a+b)×[100b+10(a+b)+a]=[100a+10(a+b)+b]×(10b+a).构建数学的知识网络学习数学,重要的是要构建一个数学的知识网络,将单一的知识都串联起来,这样有助于对综合型题目的解答。

初中数学试卷金戈铁骑整理制作探索规律练习题一 细心观察，巧妙发现! 班级：学号：姓名：1. （2009年贵州黔东南州）某校生物教师李老师在生物实验室做试验时，将水 稻种子分组进行发芽试验；第1组取3粒，第2组取5粒，第3组取7粒……即 每组所取种子数目比该组前一组增加 2粒，按此规律，那么请你推测第n 组应该 有种子数（）粒。

A 、2n 1B 、2n -1 G 2n D n 22. （2009年重庆）观察下列图形，则第n 个图形中三角形的个数是（ ）O H 口第1个第2个第3个3. （2009武汉）将一些半径相同的小圆按如图所示的规律摆放：第 1个图形有6 个小圆，第2个图形有10个小圆，第3个图形有16个小圆，第4个图形有240 0 ◎ ◎ OO O O 90000 O第3个图形4. （2009重庆泰江）观察下列等式:22一1.4 -1 =3父5 ;2.52 - 22 = 3 7 ;_ _2_2 _—3.62 - 32 = 3 92 2 一4.7 —4 =3父11 ;则第n （ n 是正整数）个等式为 .A. 2n+2B. 4n+4C. 4n —4D. 4n个小圆，……，依次规律，第6个图形有o o o 0第1个图形 个小圆.O I O O O O O c o o o 0 O O O O O P o o O O。

IOOO第2个图形，一一、， __ 1 2 3 4 一一5.（2009年牡丹江市）有一列数一,一，-一,一，…，那么第7个数是2 5 10 176.（2009年娄底）王婿同学用火柴棒摆成如下的三个“中”字形图案，依此规律, 第n个“中”字形图案需根火柴棒.7.(2009恩施市)观察数表11 -11 -2 11-3 3-11 -4 6 Y 11 -5 10 A 5 -11-6 15 -20 15 -6 1根据表中数的排列规律，则字母A所表示的数是:8.（2009年益阳市）图6是一组有规律的图案，第1个图案由4个基础图形组成，第2个图案由7个基础图形组成，……，第n（n是正整数）个图案中由个基础图形组成.⑴(2) ⑶图69.（2009年广州市）如图7-①，图7-②，图7-③，图7-④，…，是用围棋棋子按照某种规律摆成的一行“广”字，按照这种规律，第5个“广”字中的棋子个数是,第n个“广”字中的棋子个数是图7-①图7-② 图7-③•・图7④10 . （ 2009肇庆）观察下列各式：1 =工 M _1'5M7 2 15 7/,根据观察计算: (2n -1)(2n 1) . （n 为正整数）11. （2009年济宁市）观察图中每一个大三角形中白色三角形的排列规律，则第13. （2009年咸宁市）如图所示的运算程序中，若开始输入的x 值为48,我们发现 第1次输出的结果为24,第2次输出的结果为12,……第2009次输出的结果为12. （2009年广西梧州） 下图是用火柴棍摆成的边长分别是 1, 2, 3根火柴棍时的正方形.当边长为 n 根火柴棍时，设摆出的正方形所用的火柴棍的根数为 s,（用n 的代数式表示s ）n=114. （2009年湖北荆州）将四张花纹面相同的扑克牌的花纹面都朝上,两张一叠,并全部 看完，则共有 种不同的翻牌方式.15. （2009年山西省）下列图案是晋商大院窗格的一部分，其中上所贴的剪纸，则第n 个图中所贴剪纸的个数为 一 代表窗纸5个大三角形中白色三角形有 个.（第13题）16. （2009年广东省）用同样规格的黑白两种颜色的正方形瓷砖，按下图的方式铺地板，则第（3）个图形中有黑色瓷砖 ___________ 块，第n 个图形中需要黑色 瓷砖 __________ 块（用含n 的代数式表示）.OO OO△ △△%△出OO OO第 个图形中“△”的个数是的个数的 5倍.18. （2009年绵阳市）将正整数依次按下表规律排成四列，则根据表中的排列规律，数2009应排的位置是第 行第 列.第1列第2列 第3列第4列第1行1 2 3第2行654第3行7 8 9第4行121110图形QQ C4d %用O O C(1) ⑵口1 2丁 p3探索规律练习题二班级：学号：姓名：1. （2009年河北）古希腊著名的毕达哥拉斯学派把1、3、6、10… 这样的数称为“三角形数”，而把1、4、9、16…这样的数称为“正方形数”.从图1中可以 发现，任何一个大于1的“正方形数”都可以看作两个相邻 列等式中，符合这一规律的是（ ）2. （2009年广西钦州）一组按一定规律排列的式子:13. (2009 成者B ) 已知 a n = ---------------------- 2(n=,1, ,2 3,.记.b ) = 2(1 —a),(n 1 )b 2 =2(1—aj(1—a 2),…，b n =2(1—aj(1 —a 2)...。