第04讲第二章数列极限定义证明

第二章 数列极限引言:在第一章中我们已经指出，数学分析课程研究的对象是定义在实数集上的函数，那么数学分析用什么方法研究实数集上的函数呢？从本质上来说，这个方法就是极限。

极限思想和方法贯穿于数学分析课程的始终，几乎所有的概念都离不开极限，是我们数学分析课程的基础。

§１ 数列极限的概念教学内容：数列极限的概念，应用定义证明简单数列的极限，无穷小数列。

教学要求：使学生逐步建立起数列极限的N ε-定义的清晰概念。

深刻理解数列发散、单调、有界和无穷小数列等有关概念。

会应用数列极限的N ε-定义证明数列的有关命题，并能运用N ε-语言正确表述数列不以某实数为极限等相应陈述。

教学重点：数列极限的概念。

教学难点：数列极限的N ε-定义及其应用。

教学方法：讲授为主。

教学学时：2学时。

一、数列概念：１．数列的定义：简单的说，数列就是“一列数”，是有一定的规律，有一定次序性的“一列数”。

若函数f 的定义域为全体正整数集合N +，则称:f N R +→或+∈N n n f ),(为数列。

若记()n f n a =，则数列n n n f Λ,2,1),(=就可写作为：12,,,,n a a a L L ，简记为{}n a ，其中n a 称为该数列的通项。

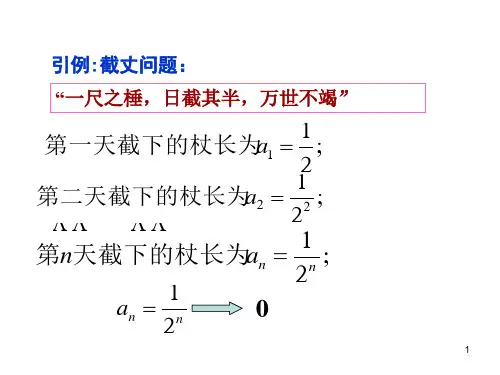
２．数列的例子：（1）(1)111:1,,,,234n n ⎧⎫---⎨⎬⎩⎭L ； （2）11111:2,1,1,1,435n ⎧⎫++++⎨⎬⎩⎭L（3）{}2:1,4,9,16,25,n L ； （4）{}11(1):2,0,2,0,2,n ++-L二、数列极限的概念：１．引言：对于这个问题，先看一个例子：古代哲学家庄周所著的《庄子. 天下篇》引用过一句话：“一尺之棰，日取其半，万世不竭”。

把每天截下的部分的长度列出如下（单位为尺）：第１天截下12，第２天截下2111222⋅=，第３天截下23111222⋅=，…，第n 天截下1111222n n -⋅=，… 得到一个数列：⎭⎬⎫⎩⎨⎧n21： 231111,,,,,2222n L L 不难看出，数列12n ⎧⎫⎨⎬⎩⎭的通项12n随着n 的无限增大而无限地接近于零。

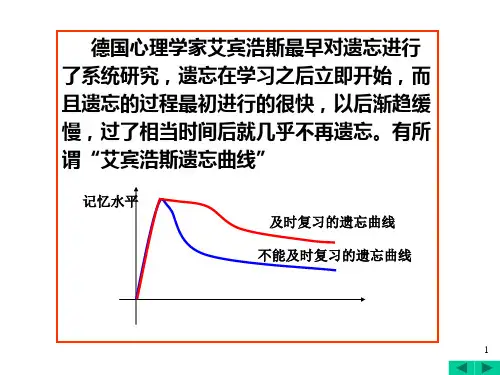
摘要：本文旨在通过对数列极限的定义进行证明，阐述数列极限的概念，并展示其数学严谨性。

首先回顾数列极限的定义，然后通过数学归纳法、夹逼定理等方法对数列极限进行证明。

一、引言数列极限是微积分学中的基本概念之一，它描述了数列在无限趋近于某一数值时的行为。

数列极限的定义为：若对于任意给定的正数ε，都存在一个正整数N，使得当n>N时，数列{an}的项与常数A的差的绝对值小于ε，则称常数A为数列{an}的极限。

本文将对数列极限的定义进行证明，以展示其数学严谨性。

二、数列极限的定义设数列{an}是定义在正整数集N上的函数，常数A是实数。

如果对于任意给定的正数ε，都存在一个正整数N，使得当n>N时，有|an - A| < ε，则称常数A为数列{an}的极限，记作：lim_{n→∞}an = A三、数列极限的证明1. 数学归纳法证明（1）当n=1时，由数列极限的定义，只需证明|a1 - A| < ε即可。

由于ε是任意给定的正数，因此当|a1 - A| < ε时，命题成立。

（2）假设当n=k（k为正整数）时，命题成立，即|ak - A| < ε。

接下来证明当n=k+1时，命题也成立。

由于|ak - A| < ε，根据数列极限的定义，存在一个正整数N1，使得当n>N1时，有|ak - A| < ε。

当n=k+1时，有：|ak+1 - A| ≤ |ak+1 - ak| + |ak - A|根据数列极限的定义，存在一个正整数N2，使得当n>N2时，有|ak+1 - ak| <ε/2。

取N = max{N1, N2}，则当n>N时，有：|ak+1 - A| ≤ |ak+1 - ak| + |ak - A| < ε/2 + ε/2 = ε因此，当n=k+1时，命题也成立。

由数学归纳法可知，对于任意正整数n，都有|an - A| < ε。

因此，根据数列极限的定义，lim_{n→∞}an = A。

数列极限的定义证明一、引言数列是由一系列有序的数按照一定规律排列而成的，数列极限是数列理论中的基本概念之一。

在数学分析中，数列极限的定义是数学推理的重要基础，也是许多数学定理的核心。

二、数列极限的定义数列极限的定义是指当数列的项趋向于某个值时，数列的极限就是这个值。

换句话说，对于数列{an}，如果对于任意给定的正实数ε，存在正整数N，使得当n>N时，|an-a|<ε，那么数列的极限就是a。

三、数列极限的重要性1. 在微积分中，数列极限是导数和积分的基础。

在求导和积分的过程中，我们需要用到极限的性质和定义来推导出相应的公式和定理。

2. 在数学分析中，数列极限是许多重要定理的基础，如泰勒级数展开、函数极限和级数收敛等。

3. 数列极限的概念也被广泛应用于物理学、工程学和经济学等应用科学领域，用于描述各种现象和模型。

四、数列极限的例子1. 递推数列：考虑递推数列{an}，其中an=an-1+2，且a0=1。

我们想要求出数列的极限。

根据递推关系，我们可以得到a1=3，a2=5，a3=7，以此类推。

显然，数列的项随着n的增大而无限增大，所以数列没有极限。

2. 有界数列：考虑数列{an}，其中an=(-1)^n/n。

我们想要求出数列的极限。

当n为偶数时，an=1/n；当n为奇数时，an=-1/n。

显然，数列的项在n趋于无穷大时趋近于0，所以数列的极限是0。

3. 收敛数列：考虑数列{an}，其中an=1/n。

我们想要求出数列的极限。

对于任意给定的正实数ε，我们可以找到一个正整数N=1/ε，使得当n>N时，|an-0|<ε。

因此，数列的极限是0。

五、数列极限的性质1. 数列极限的唯一性：如果一个数列的极限存在，那么它是唯一的。

2. 数列极限的保号性：如果数列的极限大于（小于）0，那么数列中的项大于（小于）0的项的索引之后的所有项。

3. 数列极限的有界性：如果数列的极限存在，那么数列是有界的，即存在正整数M，使得对于所有的n，|an|<M。

数列极限的概念及其性质证明数列是数学中的重要概念之一，它是由一系列按照一定规律排列的数所组成的序列。

而数列极限是数列理论中的核心概念之一，它描述了数列在无限项下的趋势和性质。

本文将探讨数列极限的概念及其性质证明。

一、数列极限的概念数列极限是指当数列的项数趋向无穷大时，数列中的数值逐渐趋近于某个固定的值。

具体地说，对于一个实数数列{an}，如果存在一个实数a，使得对于任意给定的正数ε，总存在正整数N，使得当n>N时，有|an - a| < ε成立，那么称数列{an}的极限为a，记作lim(n→∞)an = a。

二、数列极限的性质证明1. 唯一性性质首先，我们来证明数列极限的唯一性性质。

假设数列{an}的极限既为a又为b，且a ≠ b。

根据极限的定义，我们可以取ε = |a - b|/2，那么存在正整数N1和N2，使得当n > N1时，有|an - a| < ε，当n > N2时，有|an - b| < ε。

考虑n > max(N1, N2)，那么根据三角不等式，有：|a - b| = |(a - an) + (an - b)| ≤ |a - an| + |an - b| < ε + ε = |a - b|。

这与|a - b| < |a - b|矛盾，因此假设不成立，数列极限的唯一性得证。

2. 有界性性质接下来，我们证明数列极限的有界性性质。

假设数列{an}的极限为a，则存在正整数N，使得当n > N时，有|an - a| < 1。

令M = max{|a| + 1, |a1|, |a2|, ..., |aN|}，那么对于任意的n > N，有：|an| = |an - a + a| ≤ |an - a| + |a| < 1 + |a| ≤ |a| + 1 ≤ M。

因此，数列{an}是有界的。

3. 单调性性质最后，我们证明数列极限的单调性性质。

第二章函数第1节数列的极限数列极限的定义和几何解释数列的极限的定义和几何解释一、数列极限的定义.})1(1{1时的变化趋势当观察数列∞→-+-n n n 播放问题:当无限增大时,是否无限接近于某一确定的数值?如果是,如何确定?n x n .1)1(1,1无限接近于无限增大时当n x n n n --+=问题:“无限接近”意味着什么?如何用数学语言刻划它.=-1n x nn n 11)1(1=--通过上面演示实验的观察:,1001给定,10011<n 由,100时只要>n ,10011<-n x 有,10001给定,1000时只要>n ,1000011<-n x 有,100001给定,10000时只要>n ,100011<-n x 有,0>ε给定,])1[(时只要ε=>N n .1成立有ε<-n x如果数列没有极限,就说数列是发散的.数列的极限的定义和几何解释二、几点注意和几何解释注意：;.1的无限接近与刻划了不等式a x a x n n ε<-..2有关与任意给定的正数εNx 1x 2x 2+N x 1+N x 3x 几何解释:.)(,),(,落在其外个至多只有只有有限个内都落在所有的点时当N a a x N n n εε+->:定义N -ε其中;:每一个或任给的∀.:至少有一个或存在∃.,,0,0lim ε<->>∃>ε∀⇔=∞→a x N n N a x n n n 恒有时使数列的极限的定义和几何解释三、用定义证明数列的极限例1.1)1(lim 1=-+-∞→nn n n 证明证1-n x 1)1(1--+=-n n n n1=,0>ε任给,1ε<-n x 要,1ε<n 只要,1ε>n 或所以,,1]1[+=εN 取,时则当N n >ε<--+-1)1(1n n n 就有.1)1(lim 1=-+-∞→n n n n 即例2.lim ),(C x C C x n n n =≡∞→证明为常数设证C x n -C C -=,成立ε<,0>ε任给所以,0=,n 对于一切自然数.lim C x n n =∞→说明:常数列的极限等于同一常数.小结:用定义证数列极限存在时,关键是任意给定寻找N ,但不必要求最小的N .,0>ε例3.1,0lim <=∞→q q nn 其中证明证,0>ε任给,0ε<=-nn q x ,ln ln ε<q n ,]ln ln [为自然数取q N ε≥,时则当N n >,0ε<-nq 就有.0lim =∴∞→n n q ,0=q 若;00lim lim ==∞→∞→n n n q 则,10<<q 若,ln ln q n ε>∴例4.lim ,0lim ,0a x a x x n n n n n =>=>∞→∞→求证且设证,01>ε任给.lim a x n n =∞→故,lim a x n n =∞→ ,1ε<->∃∴a x N n N n 时恒有使得当a x a x a x n n n +-=-从而有a a x n -<a 1ε<ε=谢谢THANK YOU。

第一章函数与极限§1.1函数§1.2极限§1.2 极限一、数列的极限二、函数的极限…1、概念的引入一、数列的极限2、数列的定义数列的有界性.数列的几何意义.数列是整标函数数列的单调性. ()().n x f n n =→∞几何解释1、概念的引入3、数列的极限2、数列的定义4N a、定义证明数列极限为一、数列的极限P66XT1.2 2.(1, 3, 4) 3.(1) 唯一性若数列{x n }收敛,则其极限值惟一.5、收敛数列的性质(P24)(2) 有界性收敛的数列必定有界.(3) 保序性(1) 唯一性若数列{x n }收敛,则其极限值惟一.5、收敛数列的性质(2) 有界性收敛的数列必定有界.(3) 保序性推论2.lim ,lim ,,,, .n n n n n n x a y b N n N x y a b →∞→∞==∃>≥≥设且若正整数当时有则必有反证:设a <b , 由定理3, ∃正整数N 1,当n > N 1时, 有x n < y n .取N 2= max{N , N 1},则当n > N 2( ≥N )时,有x n < y n .此与条件矛盾.定理3.lim ,lim ,,,,.n n n n n n x a y b a b N n N x y →∞→∞==>∃>>设且则正整数当时有推论3:, 若∃正整数N , 当n >N 时, lim n n x a →∞=则有x n ≥0a ≥0lim 0 (lim 0)n n n n x x →∞→∞≥≤即推论1.(保号性定理) 若lim n n x a →∞=, 而a >0 (a <0). 则∃正整数N , 当n >N 时, 有x n >0 (x n <0)(1) 唯一性若数列{x n }收敛,则其极限值惟一.5、收敛数列的性质(2) 有界性收敛的数列必定有界.(3) 有序性推论…。

数列极限的定义证明数列极限是数学分析中一个重要的概念，它描述了数列中的数值逐渐趋近于某个确定的值。

而数列极限的定义则是通过一系列条件来准确定义数列的极限。

本文将通过严谨的论证，来证明数列极限的定义。

我们来回顾一下数列的定义。

一个数列是由一系列实数按照一定顺序排列而成的集合。

数列可以用数学符号表示为{a1, a2, a3, ...}，其中ai表示数列中的第i个元素。

数列有时也可以表示为{an}，其中n表示数列中的第n个元素。

数列的极限定义如下：对于一个给定的实数L，如果对于任意一个正实数ε（epsilon），存在一个正整数N（N>0），使得当n>N时，数列中的每一项与L的差的绝对值|an - L|都小于ε，那么我们称L为数列{an}的极限，记作lim(n→∞)an = L。

现在我们来证明这个定义。

首先，我们假设数列{an}的极限为L。

根据极限的定义，我们需要证明对于任意一个正实数ε，存在一个正整数N，使得当n>N时，数列中的每一项与L的差的绝对值都小于ε。

假设存在一个正实数ε>0，我们需要找到对应的正整数N，使得当n>N时，|an - L|<ε。

由于极限L存在，那么对于任意一个正实数ε，总能找到对应的正整数N1，使得当n>N1时，|a1 - L|<ε。

接下来，我们要证明对于任意一个正整数k，当n>N1时，|an - L|<ε。

我们假设存在一个正整数k，使得当n>Nk时，|an - L|≥ε。

由于数列{an}是有序排列的，所以必然存在一个最小的整数m，使得当n>Nm时，|an - L|≥ε。

现在我们来考虑数列中的子数列{ak}，其中k>N1。

由于数列是有序排列的，所以子数列{ak}中的每一项都大于等于数列{a1}中的对应项。

即对于任意一个正整数k，当n>N1时，我们有|an - L|≥|ak - L|≥ε。

这与我们的假设矛盾，所以假设不成立。

数列极限的定义证明数列的极限例1证明数列,)1(,,43,34,21,21nn n --+的极限是1.（分析：所证结论，即对任意给定的0>ε，求数)(εN N =，使得N n >时，ε<-1n x ）证：nn x n n 1)1(--+=任给0>ε，要使ε<-1n x ，只要1(1)11n n n n ε-+--=<，即ε1>n ，∴对于0>ε，取]1[ε=N ，则当N n >时，1(1)1n n n ε-+--<即10(1)lim 1.n n n n-→+-=例2证明：02lim 1.1n n n →+=+证：21n n x n +=+任给0>ε（不妨设1ε<），要使ε<-1n x ，只要21111n n n ε+-=<++，即11n ε>-∴对于0>ε，取1[1]N ε=-，则当N n >时，211n n ε+-<+即02lim 1.1n n n →+=+注：取1ε<，保证110ε->，取N 时更方便.若不限定110ε->，则取1max{[1],1}.N ε=-例3已知2(1)(1)nn x n -=+，证明数列的极限是0.证：任给0>ε，要使ε<-1n x ，只要22(1)1110(1)(1)1n n n n nε--=<<<+++，即即ε1>n ，∴对于0>ε，取]1[ε=N ，则当N n >时，2(1)0(1)nn ε--=<+即20(1)lim 0.(1)nn n →-=+在利用数列极限的定义来论证某个数是数列的极限是，重要的是对任意给定的正数ε，定义中的正整数N 确实存在，但没有必要求最小的N .如果知道n x a -小于某个量，（这个量是n 的一个函数），那么当这个量小于ε时，ε<-a x n 当然也成立.若令这个量小于ε来定出N 比较方便的话，就可以采用这种方法（称为放大法）.例4证明221lim .292n n n n n →∞+=++证222192922(29)n n n n n n n +--=++++当9n ≥时，有2229912(29)2(29)4n n n n n n n n n--=<<++++取1max{[],9}.N ε=注：第一个不等式是有条件放大（即9n ≥）；第二个不等式是无条件放大，由此可知放大不等式一般有下列要求：（1）放大后的式子应该随着n 的增大而减小，能使该式小于ε.例如，式子如果是关于n 的有理分式，则要求分母n 的次数高于分子n 的次数.（2）使最后一个式子小于ε的不等式容易解出n .例5利用数列极限的定义证明1lim 1n n n →∞=（或1lim 1,0n n a a →∞=>）.分析：由于1n n x n =，底数与指数都随着n 而变化，故不好直接求解不等式11nn ε-<.需将不等式用其它方法化简放大，使得关于解n 更容易证一：令111nn a a -==+，即222(1)(1)(1)12222n n n n n n n n n a na a a a a --=+=++++>>⋅ （当2n >）即224n a n <，亦即a <1-<ε<，即24n ε>取24max{[],2}N ε=证2依据几何平均不超过算术平均不等式12n a a a n+++≤11(2)1)1n n n n +++++--=≤==+2(1)21n n --≤<=ε<，即24n ε>，故取24[N ε=.。