两圆公切线的作图

两圆的公切线前言在几何学中，我们经常研究圆的性质。

圆是所有平面几何图形中最容易被理解的图形之一，因为它的定义很简单：所有点到给定点的距离相等。

在这篇文档中，我们将讨论如何求解两个圆的公切线问题。

两个圆的公切线考虑两个圆C1和C2，半径分别为r1和r2，圆心之间的距离为d。

我们想要求出连接这两个圆的切线两个切点的坐标。

情况1：两圆相离当两个圆不相交时，它们的公切线如下所示：既然两个圆不相交，它们的距离一定大于它们的半径之和。

因此，我们可以依次执行以下步骤来求解两个圆的公切线：1.计算d=r1+r22.计算sinθ=r2/d3.计算cosθ=r1/d4.对于每个值θ∈[0,π)，计算切点的坐标根据上述步骤可以得到两个切点的坐标，它们分别为：(x1,y1)和(x2,y2)。

情况2：两圆内含当一个圆完全包含在另一个圆之内时，两个圆的公切线如下所示：在这种情况下，我们可以依次执行以下步骤来求解两个圆的公切线：1.计算d=r1-r22.计算sinθ=r2/d3.计算cosθ=r1/d4.对于每个值θ∈[0,π)，计算切点的坐标在这种情况下，我们只有外部切线。

情况3：两圆相交当两个圆相交时，它们的公切线如下所示：我们可以依次执行以下步骤来求解两个圆的公切线：1.计算d=√((x2-x1)2+(y2-y1)2)2.计算α=asin((r1-r2)/d)3.计算β=tan^(-1)((y2-y1)/(x2-x1))4.对于θ=β+α和θ=β-α，计算切点的坐标请注意，如果两个圆的半径相等，则α=π/4，这是一个非常特殊的情况。

结论本文讨论了如何计算两个圆的公切线。

对于不相交的圆，我们可以直接计算出切点的坐标。

对于相交的圆，我们必须考虑两个角度，以计算出正确的公切线。

如果您对本文所述内容有任何问题或意见，请在评论区中留言。

感谢您的阅读！。

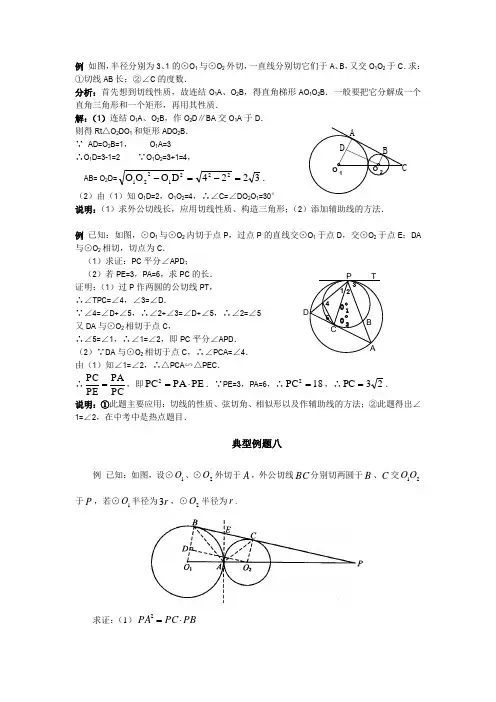
例 如图，半径分别为3、1的⊙O 1与⊙O 2外切，一直线分别切它们于A 、B ，又交O 1O 2于C ．求：①切线AB 长；②∠C 的度数．分析：首先想到切线性质，故连结O 1A 、O 2B ，得直角梯形AO 1O 2B ．一般要把它分解成一个直角三角形和一个矩形，再用其性质． 解：（1）连结O 1A 、O 2B ，作O 2D ∥BA 交O 1A 于D ． 则得Rt △O 2DO 1和矩形ADO 2B ． ∵ AD=O 2B=1， O 1A=3 ∴O 1D=3-1=2 ∵O 1O 2=3+1=4， AB= O 2D=3224D O O O 2221221=-=-．（2）由（1）知O 1D=2，O 1O 2=4，∴∠C=∠DO 2O 1=30° 说明：（1）求外公切线长，应用切线性质、构造三角形；（2）添加辅助线的方法．例 已知：如图，⊙O 1与⊙O 2内切于点P ，过点P 的直线交⊙O 1于点D ，交⊙O 2于点E ；DA 与⊙O 2相切，切点为C ．（1）求证：PC 平分∠APD ；（2）若PE=3，PA=6，求PC 的长． 证明：（1）过P 作两圆的公切线PT ， ∴∠TPC=∠4，∠3=∠D ． ∵∠4=∠D+∠5，∴∠2+∠3=∠D+∠5，∴∠2=∠5 又DA 与⊙O 2相切于点C ， ∴∠5=∠1，∴∠1=∠2，即PC 平分∠APD ．（2）∵DA 与⊙O 2相切于点C ，∴∠PCA=∠4．由（1）知∠1=∠2，∴△PCA ∽△PEC ． ∴PCPA PE PC =，即PE PA PC 2⋅=．∵PE=3，PA=6，∴18PC 2=，∴23PC =． 说明：①此题主要应用：切线的性质、弦切角、相似形以及作辅助线的方法；②此题得出∠1=∠2，在中考中是热点题目．典型例题八例 已知：如图，设⊙1O 、⊙2O 外切于A ，外公切线BC 分别切两圆于B 、C 交21O O 于P ，若⊙1O 半径为r 3，⊙2O 半径为r .求证：（1）PB PC PA ⋅=2O 1O 2A B CD O 1O 2A C BTP 12345（2）求P cos 的值。

怎样确定两圆的内公切线和外公切线答：首先应弄清公切线、内公切线和外公切线等概念．和两个圆都相切的直线，叫做两圆的公切线．两个圆在公切线同旁时，这样的公切线叫做外公切线图1(1)．两个圆在公切线6d22aeae8db846b70d2b475bba1b063c两旁时，这样的公切线叫做内公切线图1(2)．根据定义可以分清什么是两圆的内公切线，什么是两圆的外公切线．由于两圆的位置不同，这两圆的公切线条数也不相同．下面分别讨论．(1)当两圆外离时，可以作两条外公切线和两条内公切线，故共有4条公切线；(2)当两圆外切时，可以作两条外公切线和1条内公切线，故共有3条公切线；(3)当两圆相交时，可以作两条外公切线，而无法作出内公切线，故共有2条公切线；(4)当两圆内切时，只可作1条外公切线，而无法作两圆的内公切线，故共有1条公切线；(5)当两圆内含时，没有公切线．反过来，若两圆有4条、3条、2条、1条、没有公切线时，也可判定两圆的位置关系分别是外离、外切、相交、内切、内含．介绍两圆相外离时公切线的作法如下．作两圆的公切线，关键是作出切点，解决问题的方法是把它转化为过一点作圆的切线问题．可以想像把两圆中较小的一个圆的半径逐渐变小，最后成为一个点的情况；与小圆半径变小的同时，大圆的半径也相应地变小相等的长度，可结合画图，得到作相离两圆的外公切线转化为过圆外一点作圆(辅助圆)的切线．所以得出要先作出和大圆同心，并且半径等于两半径之差的辅助圆．如图2所示，画两个圆的公切线时，总是以较大的圆的圆心为圆心，先画一个辅助圆．如果是画外公切线．那么辅助圆的半径等于两圆半径的差；如果要画的是内公切线，那么辅助圆的半径等于两圆半径的和．辅助圆画好后，再从较小的圆的圆心作辅助圆的切线，连结切点和较大圆的圆心的线段，使之与较大圆相交于一点(画外公切线时要延长)，然后过这交点画辅助圆的切线的平行线，就得到要画的公切线．总之，画外公切线和画内公切线的方法是一样的，只是辅助圆的半径不同．当两圆外切、两圆相交时两圆外公切线的作法与两圆外离时的作法基本相同．想一想两圆外切时内公切线的作法(过切点作两圆连心线的垂线)．1421-1638-9529-3184。

第三课时两圆的公切线（三）教学目标：（1）理解两圆公切线在解决相关两圆相切的问题中的作用, 辅助线规律，并会应用；（2）通过两圆公切线在证明题中的应用，培养学生的分析问题和解决问题的水平．教学重点：会在证明两圆相切问题时，辅助线的引法规律，并能应用于几何题证明中．教学难点：综合知识的灵活应用和综合水平培养．教学活动设计（一）复习基础知识（1）两圆的公切线概念．（2）切线的性质，弦切角等相关概念．（二）公切线在解题中的应用例1、如图，⊙O1和⊙O2外切于点A，BC是⊙O1和⊙O2的公切线，B，C为切点．若连结AB、AC会构成一个怎样的三角形呢？观察、度量实验（组织学生实行）猜测：（学生猜测）∠BAC=90°证明：过点A作⊙O1和⊙O2的内切线交BC于点O．∵OA、OB是⊙O1的切线，∴OA=OB．同理OA=OC．∴OA=OB=OC．∴∠BAC=90°．反思：（1）公切线是解决问题的桥梁，综合应用知识是解决问题的关键；（2）作两圆的公切线是常见的一种作辅助线的方法．例2、己知：如图，⊙O1和⊙O2内切于P，大圆的弦AB交小圆于C，D．求证：∠APC＝∠BPD．分析：从条件来想，两圆内切，可能作出的辅助线是作连心线O1O2，或作外公切线．证明：过P点作两圆的公切线MN．∵∠MPC=∠PDC，∠MPN=∠B，∴∠MPC－∠MPN=∠PDC－∠B，即∠APC＝∠BPD．反思：（1）作了两圆公切线MN后，弦切角就把两个圆中的圆周角联系起来了．要重视MN的“桥梁”作用．（2）此例证角相等的方法是利用已知角的关系计算．拓展：（组织学生研究，培养学生深入研究问题的意识）己知：如图，⊙O1和⊙O2内切于P，大圆⊙O1的弦AB与小圆⊙O2相切于C点．是否有：∠APC＝∠BPC即PC平分∠APB．答案：有∠APC＝∠BPC即PC平分∠APB．如图作辅助线，证明方法步骤参看典型例题中例4．（三）练习练习1、教材145练习第2题．练习2、如图，已知两圆内切于P，大圆的弦AB切小圆于C，大圆的弦PD过C点．求证：PA·PB=PD·PC．证明：过点P作两圆的公切线EF∵AB是小圆的切线，C为切点∴∠FPC=∠BCP，∠FPB=∠A又∵∠1=∠BCP-∠A ∠2=∠FPC-∠FPB∴∠1=∠2 ∵∠A=∠D，∴△PAC∽△PDB∴PA·PB=PD·PC说明：此题在例2题的拓展的基础上解得非常容易．（三）总结学习了两圆的公切线，应该掌握以下几个方面1、由圆的轴对称性，两圆外(或内)公切线的交点(假如存有)在连心线上．2、公切线长的计算，都转化为解直角三角形，故解题思路主要是构造直角三角形．3、常用的辅助线：（1）两圆在各种情况下常考虑添连心线；（2）两圆外切时，常添内公切线；两圆内切时，常添外公切线．4、自己要有深入研究问题的意识，持续反思，持续归纳总结．（四）作业教材P151习题中15，B组2．探究活动问题：如图1，已知两圆相交于A、B，直线CD与两圆分别相交于C、E、F、D．(1)用量角器量出∠EAF与∠CBD的大小，根据量得结果，请你猜测∠EAF与∠CBD的大小之间存有怎样的关系，并证明你所得到的结论．(2)当直线CD的位置如图2时，上题的结论是否还能成立?并说明理由．(3)假如将已知中的“两圆相交”改为“两圆外切于点A”，其余条件不变（如图3），那么第（1）题所得的结论将变为什么？并作出证明．提示：（1）（2）（3）都有∠EAF+∠CBD=180°．证明略（如图作辅助线）．说明：问题从操作测量得到的实验数据入手，实行数据分析，归傻贸霾孪耄っ鞑孪氤闪ⅲ庖彩?a href=://teachercn/Class/034/ target=_blank>数学发现的一种方法．第(2)、(3)题是对第(1)题结论的推广和特殊化．第(3)题中若CD移动到与两圆相切于点C、D，那么结论又将变为∠CAD＝90°．数学教案－两圆的公切线。

相离的两圆的公切线的做法摘要：我们知道，相离的两个定圆(⊙O 1 半径为r 、⊙O 2半径为R)具有两条内公切线和两条外公切线。

那么，我们该如何运用尺规作图，作出这些公切线呢？在这里，将介绍几种做公切线的作法，分别运用了位似的性质、相似三角形的性质、构造矩形和结合位似和相似三角形。

其中最主要的原理是直径所对的角是直角。

一、运用位似的性质。

我们知道任意的两个圆都会位似且最多存在两个位似中心（即位似点），而由位似的定义我们知道，在两个位似的图形中，所有具有相同性质的点会交于一个点，就是位似点。

那么，由位似点引出的一条直线，它与两个位似图形的交点应该也具有相同的性质。

所以运用位似的这一性质，我们可以先找出两定圆的连心线，并作圆心在连心线上的垂线，找出了两个具有相同性质的点，这两点所在的直线与连心线的交点，就是位似中心。

此时，我们以位似点和某一圆的圆心为直径作圆,由直径所对的角为直角，那么我们可以得到该圆的一条切线，又由位似的性质知，该切线与另一圆也相切。

作法：1.连结O 1O 2，并延长。

2.过O 1、O 2作O 1O 2的垂线，分别交⊙O 1、⊙O 2于点A 1A 2。

（注：当作外公切线的时候A 1A 2取在O 1O 2的同一侧，当作内公切线的时候取在O 1O 2的不同侧）3.连结A 1A 2并延长，交O 1O 2于点O 。

4.以OO 1为直径作圆，交⊙O 1于点B 1、B 3。

5.连结OB 1并延长交⊙O 2于点B 2，连结OB 3并延长交⊙O 2于点B 4 6．则B 1B 2、B 3B 4为两圆的公切线证明：在位似的⊙O 1、⊙O 2中，已知A 1O 1、A 2O 2 都垂直于O 1O 2，则垂线A 1O 1和垂线A 2O 2的性质相同，它们两端点的连线交于位似点O 又OO 1为直径，∠OB 1O 1 =90°∵OB 1B 2在同一直线上 ∴B 1B 2两点的性质相同 ∴∠OB 1O 1 =∠OB 2O 2 =90°∴B 1B 2为两圆的公切线，同理B 3B 4也为两圆的公切线。

尺规作图——正多边形及两圆公切线作法探究海南中学高一（1）班洪璐陈洁盈成果论文自古时候起，尺规作图就是一个引人入胜的数学问题。

时至今日，这个如希腊神话般神秘的数学问题仍吸引着无数学者的目光、受到人们的重视，并且在初中课本中也渗透了一些关于基本图形的尺规作法。

但是我们并不满足于课本上的内容，并且在不断学习和探索中发现了更多关于尺规作图的问题及其解决方法，总结归纳了解决尺规作图的一般思路。

关键词尺规作图正多边形两圆的公切线希腊是奥林匹克运动的发源地。

奥运会上的每一个竞赛项目，对运动器械都有明确的规定，不然的话，就不易显示出谁“更快、更高、更强”。

一些古希腊人认为，几何作图也应像体育竞赛一样，对作图工作作一番明确的规定，不然的话，就不易显示出谁的逻辑思维能力更强。

应该怎样限制几何作图工具呢？他们认为，几何图形都是由直线和圆组成的，有了直尺和圆规，就能作出这两样图形，不需要再添加其他的工具。

于是规定在几何作图时，只准许使用圆规和直尺，并且规定只准许使用有限次。

它使用的直尺和圆规带有想像性质，跟现实中的并非完全相同：•直尺必须没有刻度，无限长，只有一只角。

只可以用它来将两个点连在一起，不可以在上画刻度。

•圆规可以开至无限宽，但上面亦不能有刻度。

它只可以拉开成你之前构造过的长度。

由于有了这样一个规定，一些普普通通的几何作图题，顷刻间变得身价百倍，万众瞩目，甚至有不少题目让西方数学家苦苦思索了2000多年。

一、几种正多边形的作法尺规作图以它特有的魅力，使无数的人沉湎其中，乐而忘返。

连拿破仑这样一位威震欧洲的风云人物，在转战南北的余暇，也常常沉醉于尺规作图的乐趣中。

有一次，他还编了一道尺规作图题，向全法国数学家挑战呢。

拿破仑出的题目是："只准许使用圆规，将一个已知圆心的圆周4等分。

"由于圆心O是已知的，求出这个题目的答案并不难。

正四边形的作法：1、在圆周上任意选一点Ａ，以A点为圆心，OA长为半径作弧，交圆O于点B；2、以点B为圆心，OA长为半径作弧，交圆O于点C；3、以点C为圆心，OA长为半径作弧，交圆O于点D；4、分别以A点和D点为圆心，AC长为半径作弧，两弧交于点M；5、用圆规量出OM的长度，以点A为起点，逐一在圆周上划分，便可将圆周4 等分。

对于建筑图、机械图来讲，CAD小白前期临摹图纸主要是熟悉自己所使用的绘图工具。

即便如此在绘图的时候也会碰到一些绘制的难点。

就说CAD中两个圆形的公切线如何绘制？感兴趣或者想学习的小伙伴不妨跟着小编一起来看下面的操作：
第一步：在我们的电脑桌面上方找到迅捷CAD编辑器图标并打开运行，之后会进入到CAD编辑器的操作界面。

在该界面上方找到新建命令，从新创建一张图纸。

第二步：或者点击界面上方的文件—打开命令，把之前没有绘制完成的图纸打开。

点击界面上方的编辑器按钮，在下拉框内我们点击圆形图标。

在图纸上方绘制出来两个圆形。

第三步：找到编辑器下方命令中的捕捉，并用鼠标进行点击。

在下面选项中选中切线命令，并用鼠标进行点击。

第四步：在图纸上找到我们所要绘制的两个圆形，然后在一个圆形上方取点做切线，然后在绘制另外一条切线。

这样两个圆形的公切线就绘制完成。

怎么样，是不是觉得其实绘制一些简单的图形也并不会特别的难。

以上内容利用迅捷CAD编辑器工具完成操作！希望对大家能够有所帮助！。

两圆的公切线(一)在几何学中，公切线是指两个圆相交时与两个圆都相切的直线。

公切线有两条，分别为内公切线和外公切线。

本篇文章将重点讨论两圆的内公切线。

一、两圆的内公切线的定义给定两个圆C1和C2，它们的内公切线是同时与C1和C2相切且不相交的直线。

二、判断两圆是否有内公切线的条件若两个圆C1和C2的半径分别为r1和r2，它们的圆心距离为d，则存在内公切线的条件如下：1.若r1=r2，即两个圆的半径相等，则两个圆的内公切线存在。

2.若r1>r2，即C1的半径大于C2的半径，则当d<r1-r2时，两个圆的内公切线存在。

3.若r1<r2，即C1的半径小于C2的半径，则当d<r2-r1时，两个圆的内公切线存在。

三、两圆的内公切线的性质1.两个圆的内公切线与两个圆的圆心连线垂直。

2.两个圆的内公切线的切点在两个圆的圆心连线上。

3.两个圆的内公切线的切点到两个圆心的距离相等。

四、两圆的内公切线的求解方法我们可以通过几何方法求解两圆的内公切线，具体步骤如下：1.连接两个圆的圆心，并根据圆心距离d与两个圆的半径r1和r2的关系，判断是否存在内公切线。

2.若存在内公切线，则在两个圆的圆心连线上取两个切点。

3.连接两个切点，并延长至两个圆上，即可得到两个内公切线。

五、两个圆的内公切线的示意图以下是两个圆的内公切线示意图。

o C1\\\\\\o C2六、结论本文简要介绍了两个圆的内公切线的定义、判断条件、性质、求解方法以及示意图。

在实际应用中，了解两个圆的内公切线的性质和求解方法可以帮助我们解决相关的几何问题。

在下一篇文章中，我们将继续讨论两圆的外公切线。

注意：本文中所提到的两个圆是指平面上的两个圆，不包括相交、相切或包含的情况。