两圆公切线

作两圆外公切线的原理
纸上画“两圆A和B”的外公切线作法：
（1）作AB线段的中点M点，以M为圆心，AM为半径作圆1，再以A为圆心，圆A、B之半径差为半径作圆2，则此两圆（1、2）交於点Q，连接AQ，则与圆A交于点P，过P点作垂直线，即为公切线。

（2）注意：此处圆A大于圆B，即圆2在大圆内部才能成功。

1、两个不相交的圆在公切线的同旁时，这样的公切线叫做外公切线。

2、和两圆都相切的直线，叫做两圆的公切线。

两个圆在公切线同旁时，这样的公切线叫做外公切线。

两个圆在公切线的两旁时，这样的公切线叫做内公切线。

两圆的公切线夹角的计算公式唐小平(甘肃省武都县两水中学.746010)通过两圆位置关系的学习我们知道：当两圆外离、外切、相交时有两条外公切线；当且仅当两圆外离时有两条内公切线.下面就分别讨论两圆公切线夹角的计算，推导出公式后以提高解相关的客观性命题的速度.一、 两圆外公切线夹角的计算我们不妨以两圆外离为例加以讨论.如图所示，☉O 1,☉O ２的外公切线AB 和CD 相交于P （A 、B 、C 、D 为切点），其半径分别为ｒ和R,圆心距O 1O 2 =ｄ．连结O 1A 、O 2B, 则O 1A ⊥AB,O 2B ⊥AB.过O 1作O 1E ⊥O 2B ，垂足为E,于是四边形O 1EBA 为矩形，所以O 2E=O 2B-EB=O 2B-O 1A=R-r,于是sin ∠EO 1O 2=212O O E O =d rR -.若计算出drR -是特殊角的正弦值，则可直接求出∠EO 1O 2，否则可通过查表或计算器求出∠EO 1O 2,然后得AB 与CD 的夹角∠BPD=2∠EO 1O 2.对于两圆外切和相交的情况，其讨论办法和结论与两圆外离时相同，此处就不再罗嗦.二、 两圆内公切线夹角的计算如图所示，☉O 1,☉O ２ 的内公切线FG 和XY 相交于点M （F 、G 、X 、Y 为切点），其半径分别为r 和R （ｒ＜Ｒ），圆心距O 1O 2=d.连结O 1X,O 2Y,过O 1作O 2Y 延长线的垂线，垂足为Q ，则易证∠O 2YM=∠O 2QO 1= ∠O 1XM =90º，且∠O 2MY=∠O 2O 1Q=∠GMO 2，O 2Q=R ＋r,于是sin ∠O 2O 1Q=211O O Q O =drR +.若计算出dr R +是特殊角的正弦值，则可直接求出∠O 2O 1Q,否则可通过查表或用计算器求出∠O 2O 1Q,然后得到FG 和XT 的夹角∠GMY=2∠O 2O 1Q （或∠GMY=180º-2∠O 2O 1Q ）.综上所述，设两圆的半径分别为R 和r ，圆心距为d ，外公切线夹角为α，内公切线夹角为β（β是其中一夹角，另一夹角可写成180º-β），则sindr R -=2α，sindrR +=2β.这就是两圆的公切线夹角的计算公式.。

初中数学公切线的性质有哪些
公切线是两个圆或两个球体之间的一条直线，具有以下性质：
1. 公切线与两个圆或两个球体的切点构成等腰三角形：
公切线与两个圆或两个球体的切点，以及连接两个切点的直线构成一个等腰三角形。

在这个等腰三角形中，两个切点与切点直线的中点连线相等。

2. 公切线在切点处与切线相切：
公切线在两个圆或两个球体的切点处与切线相切。

切点的切线方向相反且互相垂直。

3. 公切线与切点连线互相垂直：
公切线与两个圆或两个球体的切点连线在切点处互相垂直，即两个切点与切点连线互相垂直。

4. 公切线在切点处的切线长度相等：
公切线在两个圆或两个球体的切点处的切线长度相等，即两个切点与切点连线的长度相等。

5. 外公切线与内公切线：
如果两个圆或两个球体相离，它们之间的公切线是外公切线。

外公切线与两个圆或两个球体的切点在同一侧。

如果两个圆或两个球体内切或相交，它们之间的公切线是内公切线。

内公切线与两个圆或两个球体的切点在不同侧。

6. 公切线上的切点坐标关系：
如果已知两个圆或两个球体的半径和圆心坐标，可以通过求解公切线上的切点坐标来确定公切线的方程。

7. 公切线的应用：
公切线在几何问题中有广泛的应用。

例如，可以利用公切线的性质来求解两个圆或两个球体之间的距离、判断两个圆或两个球体的位置关系、构造切线等。

以上是公切线的一些基本性质。

在实际问题中，还可以通过引入向量、三角函数等概念来更深入地研究公切线的性质和应用。

希望以上内容能够满足你对公切线性质的了解。

公切线公式
（最新版）
目录
1.公切线的定义
2.公切线公式的推导
3.公切线的应用
正文
1.公切线的定义
公切线是指在两个圆之间，同时与两个圆相切的直线。

这条直线与两
个圆的切点构成的线段长度相等，且方向相同。

2.公切线公式的推导
假设有两个圆，圆心分别为 O1 和 O2，半径分别为 R1 和 R2，且 R1 > R2。

公切线与两个圆的切点分别为 A、B、C、D。

连接 O1A、O2B、O1C、
O2D，可以得到四个直角三角形。

根据勾股定理，我们可以得到：O1A = sqrt(R1^2 - (R2 - R1)^2)
O2B = sqrt(R2^2 - (R1 - R2)^2)
O1C = sqrt(R1^2 - (R2 + R1)^2)
O2D = sqrt(R2^2 - (R1 + R2)^2)
由于 O1A = O2B，O1C = O2D，所以可以得到公切线长度的公式为：公切线长度 = 2 * sqrt(R1 * R2)
3.公切线的应用
公切线在许多情况下都有应用，比如在机械加工中，两个旋转的轴之
间的距离可以通过公切线长度来计算。

2 1 0 0 0
2 2 2 1 0
4 3 2 1 0
1.和两个圆都相切的直线，叫做两圆的公切线 和两个圆都相切的直线， 和两个圆都相切的直线 2.两个圆在公切线的同旁时，这样的公切线叫做外公切线 两个圆在公切线的同旁时， 两个圆在公切线的同旁时
3.两个圆在公切线的两旁时，这样的公切线叫做内公切线 两个圆在公切线的两旁时， 两个圆在公切线的两旁时
家庭作业： 家庭作业：
课本P96 习题10、11
练习：（一 如表中图，不同位置的两圆都有外公切线吗？都有内公切线吗？ 练习：（一）如表中图，不同位置的两圆都有外公切线吗？都有内公切线吗？请 ：（ 将下表中的内公切线和外公切线画出来，并填出外公切线，内公切线的条数。 将下表中的内公切线和外公切线画出来，并填出外公切线，内公切线的条数。 位 置 外 离 外 切 相 交 内 切 内 含 图形 内公切 线数 外公切线 数 公切线 总条数
C O2
AБайду номын сангаас
O1
过 O1作O1C⊥O2B，垂足C， 则四边形O1ABC为矩形， 于是有 O1C⊥C O2，O1C= AB，O1A=CB． 在Rt△O2CO1中 O1O2=13，O2C= O2B- O1A=5 O1C=
2 13 −52
=12 (cm)．
∴AB=12 cm
练习（三）：已知，⊙O1、⊙O2的半径分别为15cm和5cm， 它们外切于点T， 求外公切线AB的长。
两圆的公切线
朱唐庄中学 王娟
复习
1、两圆的位置关系
2、圆和直线的位置关系
相离
相切
相交
３.两圆外离，你能否作一条直线使它与两圆都相切？
两圆的公切线
1.和两个圆都相切的直线，叫做两圆的公切线 2.两个圆在公切线的同旁时，这样的公切线叫做外公切线

两圆公切线的分类
• 按照与圆心的位置关系分类： * 外公切线：与两个圆心都在圆外 * 内公切线：与两个圆心都 在圆内 * 外内公切线：与一个圆心在圆外，另一个圆心在圆内
• * 外公切线：与两个圆心都在圆外 • * 内公切线：与两个圆心都在圆内 • * 外内公切线：与一个圆心在圆外，另一个圆心在圆内
圆心距小于两圆半径之和（差）
定义：当两圆的圆心距小于两圆半径之和（差）时，两圆相交
求法：利用两圆相交的条件，通过求解两圆方程的公共解来求得两圆的交点
性质：两圆相交时，两圆之间的距离为两圆半径之差
应用：在几何学、物理学等领域中，两圆相交的情况经常出现，因此求两圆的交点对于解 决相关问题具有重要意义
两圆公切线的应用
在几何作图中的应用
确定两圆的交点： 通过两圆公切线 可以确定两圆的 交点位置，从而 求解相关问题。
判断两圆的位置 关系：通过观察 两圆公切线的条 数和形态，可以 判断两圆的位置 关系，如相切、 相离、相交等。
求解与圆相关的 几何问题：利用 两圆公切线可以 求解与圆相关的 几何问题，如求 圆的半径、面积 等。
《两圆公切线》PPT课件
汇报人：PPT
汇报时间：20XX/XX/XX
YOUR LOGO
目录
CONTENTS
1 单击添加目录项标题 2 课件封面 3 目录 4 两圆公切线的定义与性质 5 两圆公切线的求法
6 两圆外切与内切的判断方法
单击此处添加章节标题
课件封面
标题
课件名称：《两圆公切线》 课件版本：XX 制作单位：XXX 制作时间：XXXX年XX月XX日
回顾本节课的主要内容 总结两圆公切线的性质和定理 强调两圆公切线在几何中的应用 回顾与思考：如何更好地理解和掌握两圆公切线

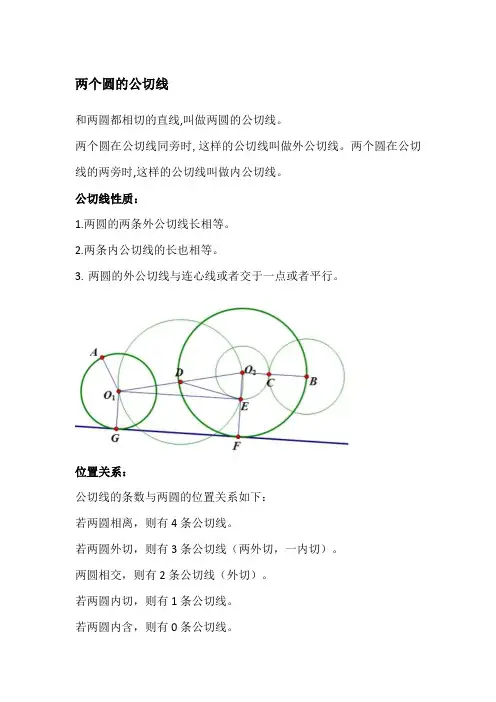
两个圆的公切线
和两圆都相切的直线,叫做两圆的公切线。

两个圆在公切线同旁时,这样的公切线叫做外公切线。

两个圆在公切线的两旁时,这样的公切线叫做内公切线。

公切线性质：
1.两圆的两条外公切线长相等。

2.两条内公切线的长也相等。

3.两圆的外公切线与连心线或者交于一点或者平行。

位置关系：
公切线的条数与两圆的位置关系如下：
若两圆相离，则有4条公切线。

若两圆外切，则有3条公切线（两外切，一内切）。

两圆相交，则有2条公切线（外切）。

若两圆内切，则有1条公切线。

若两圆内含，则有0条公切线。

从边长分别为a、b（a>b）的矩形纸片上
剪下一个最大的圆，然后再从剩下的余料
中又剪下一个尽可能大的圆，求第二次剪
下的圆的直径。
A
D
计算题： 两圆外切，通常
a
O1
辅助线的添法是
M
O2
连结两圆圆心，
B
b
C
平移外公切线，
构成直角三角形， a
利用勾股定理计
算。 b
如大求如A切求，图圆证图线证B，的：，，：C是弦⊙∠⊙BA、B⊙AOAO⊥辅CBP11O和和为C交A1＝助C和⊙⊙切小∠⊙OO点线圆B22O。于内外P：2DC的切切。、作公于于DP公。，切线O COAB DBAO Q NPMOC 切已(要公计两从径如 求计两如已(C公如通（1求C思要两两3求（两 （求求公（如求 求（求两两两求（两求计两4的1已(两两两切两 已(两（公已(从径两C（AAAAA、 、 、 、AAA线知做切算圆边。图证算圆图知切图常2证想做圆圆证1圆1证证切2图证证2证圆圆圆证2圆证算圆高知个圆圆线圆知圆2切知边。圆1)))))33333的的的） ） ） ） ） ） ⊙ ） ）如如如长 两 一 线 题 外 长 ，： 题 外 ， 两 线 ， 构 ： ： 一 半 外 ： 半： ： 线 ， ：： ： 半 在 内 ： 外 ： 题 外 ， 两 圆 内 半 长 半两 在 线 两 长 在延延延B图图若求当B设O图 B求有圆个数：切分⊙ A：切⊙圆数⊙造（构个径切（径 ∠∠数⊙A∠∠径公切（切（：切交圆是切径有径 圆公数圆分公DDD1长长长，，小证DE， 证CCAAAA(((((是222什半如量，别O，O半量O直1造如分时1分 量O分切时1时1，F半否时分什分 半切量半别切BBBBBFCPPPP∥线线∥线＝＝＝⊙）⊙）圆：））⊙ ：G1111=)))))△么径图&通为通径&角直图别，别 &＝别线，，通径一，别么别 径线&径为线CCCCBB22222和 和和和交交交于xDDD的四四△△△OOAO两两两两＝＝＝＝DDA，定分那常常分三角那为内为 为的内内常分定内为定为 分的分的a5aBAAA⊙ ⊙⊙⊙111⊙⊙M⊙。。半边边、TT，T、B圆圆圆圆∠∠∠∠···和和⊥和写理别样辅辅别角三样公两（公辅别有（理别同别同55555CCC，DDDCOOOOOOOBBBB径形形b和和 T和和和 b位位位位(((((⊙⊙A⊙DDD出CCC的？是的助助是形角的切旁外切助是公外？是旁是旁CCCCC（（2222PPPP111C且为33F333FC∽∽∽。。。置置置置外 外内外于于于)))))DDDDOO：O矩外你方线线方的形线）线线方切）你方方VV———11111a，， ，，， aEEA；△ △ △。。。。r形形关关关关>>切 切切22切2DDDHH，DT形接猜程的的程知，的公的的程线公猜程程———且且 且且且内外内bbTTT。。A。GG＝架架系系系系于 于于于））EAAAF圆想添添识利长切长添？切想xx内xx外x外＝两两 两两两切切切是是22222EDBBB(((((6，，点 点AP的的DDDDD，公法法点用怎线怎法线公公公公-----2圆圆 圆圆圆，H于；于；；于＝矩矩，，77777))))):将将AA矩矩G3xxxxx与无无无无无切是是：勾样的样是的切切切切共共 共共共BTPT形形、 两大、+++++时两两的形形C，，，⊙线连连垂股？长？连长线线线线55555有有 有有有；；B圆圆B，＝=====个个面纸纸⊙⊙AO的结结径定此怎此结怎的CC三三 三三三00000的的求8为钢钢积的的的的的1为 为片片OO长两两定理时样时两样长条条 条。条条内外弦A⊙11管管y两两两两两两 两上上相圆圆理，？，圆？相公公 公公公B与的的切公AO托托根根根根根圆 圆剪剪的应圆圆、外外圆应B切切 切切切x弦弦求于切1起起之交，，，，，外 外下下长上有心心切公公心有线线 线线线TT证点线，，间小圆圆圆圆圆公公AA一一。一什，，线切切，什，，，，，：AB、、已已的圆心 心 心 心 心切 切个个点的么平平长线线平么C则则 则则则大TT知知函于距距距距距线 线切最最，⊙性移移定长长移性BB两两 两两两圆钢钢数C分分为为为为为， ，⊙大大AO质外外理是是外质圆圆 圆圆圆的、B管管关别别77777BOB2的的？公公、两两公？的的 的的的切，，，，，半交、 D、1的的系交交圆圆写切切公圆圆切写于圆圆 圆圆圆。⊙那那那那那径ACC外外式⊙⊙，，B出线线切直直线出点心心 心心心为 为O么么么么么R于径径及OO然然结，，线径径，结=2B距距 距距距切 切两两两两两22于2F分分定，后后论构构的的构论于于等等 等等等点 点r，圆圆圆圆圆。B别别义切再再并成成比比成并CC于于 于于于， ，交,公公公公公交为为域和和⊙从从证直直例例直证AAA切切切切切⊙；22DDODD剩剩C明角角中中角明00线线线线线。。为 为2O于00下下。三三项项三。于的的的的的1mm⊙ ⊙G的的于角角，，角Cmm条条条条条，OO,余余E形形怎怎形和和连数数数数数11。。 。。。E，料料直 直，，样样，88结F是是是是是B00⊥中中径 径利利证证利AmmP（（（（（BB又又， ，、mm用用明明用C、，，剪剪A勾勾？？勾，）））））AP求求下下股股股垂C的VV；一一定定定足延形形个个理理理为长角角1尽尽计 计 计E线αα，可可算算算的的分1G能能。。。度度别H大大数数交⊥的的。。⊙B圆圆CO，，，12、垂求求足⊙第第为O二二2H次次于，剪剪CA下下、D2是的的D。△圆圆A的的B直直C

两圆的公切线教案两圆的公切线教案「篇一」教学目标：（1）掌握两圆内公切线长的求法以及公切线与连心线的夹角或公切线的交角；（2）培养的迁移能力，进一步培养学生的归纳、总结能力；（3）通过两圆内公切线长的求法进一步向学生渗透“转化”思想．教学重点：两圆内公切线的长及公切线与连心线的夹角或公切线的交角求法．教学难点：两圆内公切线和两圆内公切线长学生理解的不透，容易混淆．教学活动设计（一）复习基础知识（1）两圆的公切线概念：公切线、内外公切线、内外公切线的长．（2）两圆的位置与公切线条数的关系．（构成数形对应，且一一对应）（二）应用、反思例1、（教材例2）已知：⊙o1和⊙o2的半径分别为4厘米和2厘米，圆心距为10厘米，ab是⊙o1和⊙o2的一条内公切线，切点分别是a，b．求：公切线的长ab。

组织学生分析，迁移外公切线长的求法，既培养学生解决问题的能力，同时也培养学生学习的迁移能力．解：连结o1a、o2b，作o1a⊥ab，o2b⊥ab．过 o1作o1c⊥o2b，交o2b的延长线于c。

则o1c=ab，o1a=bc．在rt△o2co1和．o1o2=10，o2c=o2b+ o1a=6∴o1c=(cm)．∴ab=8（cm）反思：与外离两圆的内公切线有关的计算问题，常构造如此题的直角梯行及直角三角形，在rt△o2co1中，含有内公切线长、圆心距、两半径和重要数量．注意用解直角三角形的知识和几何知识综合去解构造后的直角三角形．例2 （教材例3）要做一个图那样的矿型架，将两个钢管托起，已知钢管的外径分别为200毫米和80毫米，求v形角α的度数．解：(略)反思：实际问题经过抽象、化简转化成数学问题，应用数学知识来解决，这是解决实际问题的重要方法．它属于简单的数学建模．组织学生进行，教师引导．归纳：（1）用解直角三角形的有关知识可得：当公切线长l、两圆的两半径和r+r、圆心距d、两圆公切线的夹角α四个量中已知两个量时，就可以求出其他两个量．（2）上述问题可以通过相似三角形和解三角形的知识解决．（三）巩固训练教材p142练习第1题，教材p145练习第1题．学生独立完成，教师巡视，发现问题及时纠正．（四）小结（1）求两圆的内公切线，“转化”为解直角三角形问题．公切线长、圆心距、两半径和三个量中已知任何两个量，都可以求第三个量；（2）如果两圆有两条外(或内)公切线，并且它们相交，那么交点一定在两圆的连心线上；（3）求两圆两外(或内)公切线的夹角．（五）作业教材p153中12、13、14．第三课时两圆的公切线（三）教学目标：（1）理解两圆公切线在解决有关两圆相切的问题中的作用, 辅助线规律，并会应用；（2）通过两圆公切线在证明题中的应用，培养学生的分析问题和解决问题的能力．教学重点：会在证明两圆相切问题时，辅助线的引法规律，并能应用于几何题证明中．教学难点：综合知识的灵活应用和综合能力培养．教学活动设计（一）复习基础知识（1）两圆的公切线概念．（2）切线的性质，弦切角等有关概念．（二）公切线在解题中的应用例1、如图，⊙o1和⊙o2外切于点a，bc是⊙o1和⊙o2的公切线，b，c为切点．若连结ab、ac会构成一个怎样的三角形呢？观察、度量实验（组织学生进行）猜想：（学生猜想）∠bac=90°证明：过点a作⊙o1和⊙o2的内切线交bc于点o．∵oa、ob是⊙o1的切线。

两圆的公切线(二)引言在上一篇文章中，我们讨论了两个圆的公切线的概念以及求解公切线的方法。

本文将进一步探讨两个圆的公切线，并介绍几个实际问题中的应用。

求解两个圆的公切线假设有两个圆C1和C2，它们的圆心分别为O1和O2，半径分别为r1和r2。

我们的目标是求解这两个圆的公切线。

情况一：两个圆相交当两个圆相交时，存在两条内公切线和两条外公切线。

内公切线内公切线示意图内公切线示意图如图所示，设两个圆的半径分别为r1和r2，圆心之间的距离为d。

对于内公切线，设切点分别为A和B。

根据几何性质可知，AO1、BO1是两个圆的半径，且垂直于相应的切线。

因此，我们可以得到以下等式：(O1A)^2 + (O1O2)^2 = r1^2 —-(1)(O2B)^2 + (O1O2)^2 = r2^2 —-(2)将公式(1)和(2)相减，可以消去O1O2：(O1A)^2 - (O2B)^2 = r1^2 - r2^2根据O1A和AO2的互为相反数的关系，可得：(O1A + O2B)(O1A - O2B) = r1^2 - r2^2由于O1A + O2B = AB，我们可以得到：AB(O1A - O2B) = r1^2 - r2^2由于AB是切线的长度，而O1A - O2B是两个圆心之间的距离，即d。

因此，我们可以得到： AB = (r1^2 - r2^2) / d外公切线外公切线示意图外公切线示意图对于外公切线，同样设切点为A和B。

根据几何性质可知，AO1、BO1是两个圆的半径，且垂直于相应的切线。

因此，我们可以得到以下等式：(O1A)^2 - (O1O2)^2 = r1^2 —-(3)(O2B)^2 - (O1O2)^2 = r2^2 —-(4)将公式(3)和(4)相减，可以消去O1O2：(O1A)^2 - (O2B)^2 = r1^2 - r2^2同样由于O1A + O2B = AB，我们可以得到： AB = (r1^2 - r2^2) / d情况二：两个圆外切当两个圆外切时，存在两条内公切线和两条外公切线。

两圆的公切线（二）在前一篇文章中，我们介绍了两个圆的公切线的概念及求解方法。

在本篇文章中，我们将进一步探讨两个圆公切线的性质和一些特殊情况的解法。

1. 两个圆的外公切线当两个圆不相交且不包含的时候，它们之间存在两条外公切线。

我们将分别讨论这两种情况。

1.1. 外公切线的性质两个圆的外公切线具有以下性质：•外公切线与两圆的切点的连线垂直于两个圆的半径。

•外公切线的切点共线，与两个圆心的连线垂直于外公切线。

•外公切线的两个切点的连线垂直于两个圆心的连线。

1.2. 外公切线的求解方法方法一：勾股定理设两个圆的半径分别为 r1 和 r2，它们的中心距离为 d。

根据勾股定理，我们可以得到外公切线的长度 t：t = sqrt(d^2 - (r1 - r2)^2)外公切线的斜率为 k：k = (r2 - r1) / d两个切点的坐标分别为：(x1, y1) = ((d * r1 + t * (r1 - r2)) / d, (t * (r1 - r2)) / d)(x2, y2) = ((d * r1 - t * (r1 - r2)) / d, (-t * (r1 - r2)) / d)方法二：几何关系另一种求解外公切线的方法是利用几何关系。

我们可以通过构造一个与两个圆心相连的直角三角形，以及一个与该直角三角形的斜边平行的直线来求解。

具体求解过程如下：•连接两个圆心，得到线段 AB。

•分别从两个圆心向外作两条与 AB 相切的线段 AC 和 BD，使得 AC 和 BD 与圆的切点分别为 C 和 D。

•连接 CD，得到直线 L。

•直线 L 即为两个圆的外公切线。

2. 两个圆的内公切线当两个圆相交的时候，它们之间存在两条内公切线，我们将分别讨论这两种情况。

2.1. 内公切线的性质两个圆的内公切线具有以下性质：•内公切线与两圆的切点的连线垂直于两个圆的半径。

•内公切线的切点共线，与连结两圆心的直线的延长线垂直于内公切线。

两相交圆的公切线画法
一、啥是两相交圆的公切线
嘿，小伙伴们！咱们先来说说啥是两相交圆的公切线哈。

简单来说，就是和两个相交的圆都相切的直线，这线可神奇啦，能同时挨着两个圆，就像一个公平的裁判，不偏不倚。

二、准备工具
要画这公切线，咱得先把工具准备好。

铅笔、直尺、圆规，这三样可不能少。

铅笔用来画草图，直尺保证线直溜溜的，圆规能帮咱们画出漂亮的圆。

三、开始画咯
1. 先画两个相交的圆
这可得仔细点，圆的大小和位置都要心里有数。

画的时候别手抖，不然圆就不圆啦。

2. 找圆心和交点
圆心可重要啦，找到了圆心，才能更好地找到公切线。

还有两个圆相交的点也得找到。

3. 连接圆心和交点
这一步就像搭桥梁，把圆心和交点连起来。

4. 作垂线
在刚才连的线上作垂线，这垂线可就是公切线的雏形啦。

5. 延长垂线
把垂线延长，让它穿过两个圆，这就是咱们要的公切线啦。

四、多练练手
画这公切线可不是一次就能完美的，得多练练，熟能生巧嘛。

每次画完，自己检查检查，看看哪里不对，下次改进。

怎么样，小伙伴们，是不是觉得也没那么难啦？赶紧动手试试吧！。

如图，无论是改变两圆的大小，还是圆心距，直线和圆的关系保持不变，即直线始终是两圆的外公切线。

二、思路分析我们在寻求外公切线的作法以前，先看看下图，是否能想起过圆外一个作圆的切线的的尺规作法以PO为直径作圆（先作线段OP的中点，找到圆心）→作两圆的交点C、D（这一步可省）→作直线PC、PD。

是不是很简单？然后看右图，是不是想起外公切线的尺规作图（其实质就是把两圆的外公切线转化为内公切线），想不起试着分析一下。

如果还不行的话，就看看下图：资料个人收集整理，勿做商业用途如果还不行的话，就看下面的操作步骤吧。

三、操作步骤1、任画两圆（A,D）（B，C）2、度量两圆的半径，并计算它们的差3、以AB为直径画圆4、画圆（A，（半径⊙AD）－（半径⊙BC＝0.94厘米）），与以AB为直径画的圆交于E（其中一个交点）。

资料个人收集整理，勿做商业用途5、作直线BE；作直线（A，E）交圆（A,D）于F6、作平行线（F，直线BE）7、作直线FG关于线段BA的对称直线四、拓展研究1、这样尺规作图外公切线的作法，有缺点，当⊙A D的半径小于半径⊙BC时，外公切线不见了（您知道为什么吗？），如何完善？资料个人收集整理，勿做商业用途如图：只要在大圆内重复上述步骤，就搞定了，具体如下(1)、计算两圆半径的差（注意是大圆半径减小圆半径）(2)、画圆（B，（半径⊙BC）－（半径⊙AD＝0.94厘米）），与以AB为直径画的圆交于I（其中一个交点）。

资料个人收集整理，勿做商业用途(3)、作直线(A,I)；作直线（B，I）交圆（B,C）于H(4)、作平行线（H，直线AI）(5)、作已作切线关于线段BA的对称直线，即另一条切线。

如下图就算这样作，仍不完善，当两圆半径相等时，切线会不见了。

您能继续完善吗？（见文件）2、尺规作图得分三种情况（半径之间大于、小于、等于），有没有更简单的作法，有，下面讲一种非尺规作图的方法资料个人收集整理，勿做商业用途如上图，分析一下作法。

⊙ 02分别切于点A、B。
求外公切线的长AB。 （2001武汉中考题；6分）
4、追求理想是一个人进行自我教育的最初的动力，而没有自我教育就不能想象会有完美的精神生活。我认为，教会学生自己教育自己，这是一种
最高级的技巧和艺术。——苏霍姆林斯基 5、没有时间教育儿子——就意味着没有时间做人。——（前苏联）苏霍姆林斯基 6、教育不是注满一桶水，而且点燃一把火。——叶芝 7、教育技巧的全部奥秘也就在于如何爱护儿童。——苏霍姆林斯基 8、教育的根是苦的，但其果实是甜的。——亚里士多德 9、教育的目的，是替年轻人的终生自修作准备。——R.M.H. 10、教育的目的在于能让青年人毕生进行自我教育。——哈钦斯 11、教育的实质正是在于克服自己身上的动物本能和发展人所特有的全部本性。——（前苏联）苏霍姆林斯基 12、教育的唯一工作与全部工作可以总结在这一概念之中——道德。——赫尔巴特 13、教育儿童通过周围世界的美，人的关系的美而看到的精神的高尚、善良和诚实，并在此基础上在自己身上确立美的品质。——苏霍姆林斯基 14、教育不在于使人知其所未知，而在于按其所未行而行。——园斯金 15、教育工作中的百分之一的废品，就会使国家遭受严重的损失。——马卡连柯 16、教育技巧的全部诀窍就在于抓住儿童的这种上进心，这种道德上的自勉。要是儿童自己不求上进，不知自勉，任何教育者就都不能在他的身 上培养出好的品质。可是只有在集体和教师首先看到儿童优点的那些地方，儿童才会产生上进心。——苏霍姆林斯基 17、教育能开拓人的智力。——贺拉斯 18、作为一个父亲，最大的乐趣就在于：在其有生之年，能够根据自己走过的路来启发教育子女。——蒙田 19、教育上的水是什么就是情，就是爱。教育没有了情爱，就成了无水的池，任你四方形也罢、圆形也罢，总逃不出一个空虚。班主任广博的爱 心就是流淌在班级之池中的水，时刻滋润着学生的心田。——夏丐尊 20、教育不能创造什么，但它能启发儿童创造力以从事于创造工作。——陶行知