图上作业法专题

奇偶点图上作业法奇偶点图作业法(graphical method based on an odd-even-point approach)是求最优邮递路线的一种方法。

方法介绍其特点是:对有奇点的街道，方法是求邮递员递送邮件的路线为最短.设在某条路线中的边w, , v;〕上重复走了几次，在v;,v，之间增加几条边，令每条边的权和原来的权相等，并把新增加的边称为重复边.这样，就把原问题变为:在一个有奇点的图中，要求增加一些重复边，使新图不含奇点，并且重复边的总权为最小.把使新图不含奇点而增加的重复边，简称可行(重复边)方案.使总权最小的可行方案称为最优方案。

转变方法1.第一个可行方案的确定方法.若图中有奇点，则把它配成对，每一对奇点之间必有一条链，把这条链的所有边作为重复边加到图中去，新图中必无奇点.便给出了第一个可行方案.2.调整可行方案，使重复边总长度下降.当边w,,v;]上有两条或两条以上的重复边时，从中去掉偶数条，得到一个总长度较小的方案.于是，有:1)在最优方案中，图的每条边上最多有一条重复边.2)在最优方案中，图中每个圈上的重复边的总权不大于该圈总权的一半.3.判断最优方案的标准一个最优方案一定是满足上述1)和2)的可行方案.反之，一个可行方案若满足上述1)和2)，则这个可行方案一定是最优方案.根据判断标准，对给定的可行方案，检查它是否满足上述条件1)和2).若满足，所得方案即为最优方案;若不满足，则对方案进行调整，直至上述条件1)和2)均得到满足时为止.例子：求图 G 的最优环游①配对图 G 中有 6 个奇点 v2,v4,v5,v7,v9,v10 ，把它们配成三对： v2 与 v5 ， v4 与 v7 ， v9 与 v10 。

②添加重边，去掉奇点在图 G 中，取一条连接 v2 与 v5 的路 v2v3v4v5 ，把边 (v2,v3) , (v3,v4) , (v4,v5) 作为重复边加入图中；再取 v4 与 v7 之间一条路 v4v5v6v7 ，把边 (v4,v5) , (v5,v6) ， (v6,v7) 作为重复边加入图中；最后在 v9 和 v10 之间加一条重复边 (v9,v10) ，则图中没有奇点，是一个欧拉图。

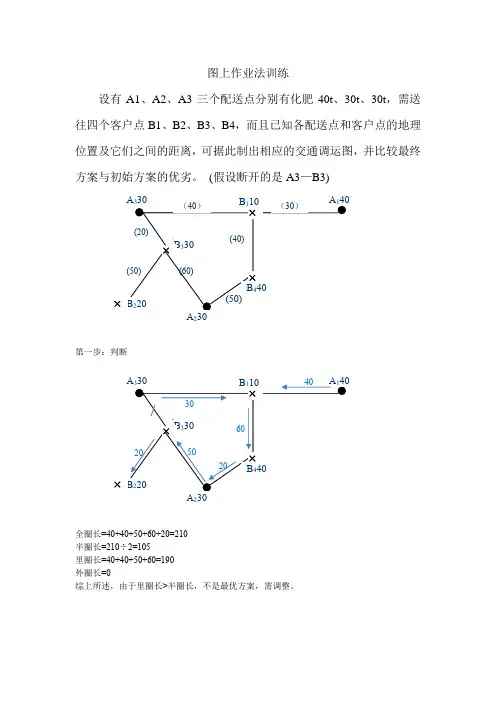
图上作业法训练设有A1、A2、A3三个配送点分别有化肥40t 、30t 、30t ，需送往四个客户点B1、B2、B3、B4，而且已知各配送点和客户点的地理位置及它们之间的距离，可据此制出相应的交通调运图，并比较最终方案与初始方案的优劣。

(假设断开的是A3—B3)第一步：判断全圈长=40+40+50+60+20=210半圈长=210÷2=105里圈长=40+40+50+60=190外圈长=0综上所述，由于里圈长>半圈长，不是最优方案，需调整。

(20)(50) (40) A 330B 110 A 140 B 440B 330B 220A 230（40） （30） (60)(50) × × × × A 330B 110 A 140 B 440B 330 B 220 A 230×× × × 3040 60 50 2020第二步：调整全圈长=40+40+50+60+20=210半圈长=210÷2=105里圈长=40+40+60=140外圈长=20综上所述，由于里圈长>半圈长，不是最优方案，需再调整。

第三步：再调整全圈长=40+40+50+60+20=210半圈长=210÷2=105里圈长=40+60=100外圈长=70综上所诉，外圈长和里圈长都小于半圈长，为最优方案。

A 330B 110 A 140 B 440B 330 B 220A 230××× × 201040 20 40 30 A 330B 110 A 140 B 440B 330 B 220 A 230××× × 3030 20 40 20 10。

平法梁图上作业法一、目标1、这是一种手工计算钢筋的方法。

目标是：根据“平法梁”的原始数据，计算钢筋。

2、原始数据：①轴线数据、柱和梁的截面尺寸；②“平法梁”集中标注和原位标注的数据。

3、计算结果：钢筋规格、形状、细部尺寸、根数。

二、工具1、多跨梁柱的示意图，不一定按比例绘制，只要表示出轴线尺寸、柱宽及偏中情况；2、梁内钢筋布置的“七线图”（一般为上3线下4线），要求不同的钢筋分线表示；3、图的下方空地用作中间数据的计算，图中原始数据用黑字表示，中间数据用红字表示。

三、步骤1、按一道梁的实际形状画出多跨梁柱的示意图，包括梁的“七线图”框架；2、按照“先定性、后定量”的原则，画出梁的各层上部纵筋和下部纵筋的形状和分布图，同层次的不同形状或规格的钢筋要画在不同的“线”上，梁两端的钢筋弯折部分要按构造要求逐层向内缩进；【注】缩进的层次由外向内分别为：梁的第一排上部纵筋、第二排上部纵筋、第一排下部纵筋、第二排下部纵筋。

3、标出每种钢筋的根数；（图一）【定性分析实例】以KL5（3）为例：那是一个3跨的框架梁，无悬挑。

先分析上部纵筋：(1)在集中标注中声明上部通长筋为2φ22 ；(2)注意到第二跨的跨中上部进行了原位标注6φ22 4/2 ，表示该跨左支座到右支座整个上部纵筋贯通，第一排纵筋4根，其中有两根为集中标注中声明的上部通长筋，另外2φ22为局部贯通，第二排2φ22为局部贯通；(3)同时注意到第一跨的右支座和第二跨的左支座的原位标注均为6φ22 4/2 ，除了两根为集中标注中声明的上部通长筋，余下的第一排2φ22 与第二跨的2φ22形成局部贯通，余下的第二排2φ22 与第二跨的2φ22形成局部贯通，这里的第一排和第二排的两种局部贯通筋由于Ln1/3 和Ln1/4 而形成了长度差别；(4)同样，第三跨的左支座和第二跨的右支座的原位标注均为6φ22 4/2 ，除了两根为集中标注中声明的上部通长筋以外，余下的第一排2φ22 与第二跨的2φ22由于Ln1/3 和Ln1/4 而形成了长度差别；(5)同时，第一跨的左支座和第三跨的右支座的上部纵筋伸入端支座，伸到柱纵筋内侧后弯直钩15d ，这些15d弯钩在端支座外侧形成了第一层和第二层的垂直层次；上部纵筋分析完了，下面分析下部纵筋：(6)第一跨的下部原位标注为6φ22 2/4 ，表示第一排下部纵筋为4φ22 ，第二排下部纵筋为2φ22 ，它们向右伸入中间支座的长度为0.5hc+5d 和LaE 的最大者，向左伸入端支座尽量伸到外侧，其15d弯钩在端支座外侧形成了第三层和第四层的垂直层次；(7)第二跨下部原位标注为2φ20 ，我们注意到第三跨的下部原位标注为7φ20 3/4 ，执行钢筋配筋的“连通原则”，我们把第二跨2φ20 的下部纵筋和第三跨第一排下部纵筋4φ20中的2φ20进行局部贯通处理；(8)第三跨的下部原位标注为7φ20 3/4 ，表示第一排下部纵筋为4φ20 ，除了和第二跨的2φ20局部贯通以外，还余下2φ20 ，第二排下部纵筋为3φ20 ，它们向左伸入中间支座的长度为0.5hc+5d 和LaE 的最大者，向右伸入端支座尽量伸到外侧，其15d弯钩在端支座外侧形成了第三层和第四层的垂直层次；(9)至此，KL5（3）纵向钢筋的定性分析全部完成。

规划商品运输方案的数学方法合理地规划产销联系是实现商品合理运输的重要手段之一。

商品产销联系规划，实质上就是为各种商品规化最有利的供应范围和流通路径，把生产地和销售地之间的联系具体化。

因此合理规划产销联系的基本原则是：在满足需要的前提下，使商品的运输费用最小或运输吨公里最少。

1．运输问题的数学模型假如某运输企业，要将某种商品从m 个产地，即A 1、A 2、……、A m ；运往n 个销售地，即B 1、B 2、……、B n 已知产地A i （i=l 、2、……、m ）的发运量为a i （i=1、2、……、m ），销售地B j （j=1、2、……、n ）的需要量为b j （j=1、2、……、n ）。

并且每个生产地到各售地的单位运价为C ij （i=1、2、……、m ，；j=1、2、……、n ）；运输距离为 L ij （i=1、2、……、m ，j=l 、2、……、n ）。

问应如何规划运输方案，是总的运费最低或运输吨公里最小？ 在此仅讨论产销平衡问题的数学模型。

当产销平衡时，总的生产量=总的销售量； 单位运价=C ij假设从生产地Ai 运往销售地Bj 的商品数量为Xij （i=1、2、……、m ，j=l 、2、…… 、n ），当目标函数为最小运输费用时，目标函数可表示为： Smin =C 11X 11+…+C 1n ·X 1n +C 21·X 21…+C 2n ·X 2n +…+C m1·X m1+…Cmn·Xmnm n= ∑ ∑ C ij ·X ij j=1 i=1同理，当目标函数为总运输吨公里最小时，目标函数可表示为：m nSmin = ∑ ∑ L ij ·X ij j=1 i=1约束条件为：n∑ X ij =ai ，i=l 、2、……、mj=1（表示从每个产地运往各个销地的商品数量之和，即等于此产地的总产量）m∑ X ij =bj ，j=l 、2、……、n i=1（表示从各个产地运到某个销地的商品数量之和，即等于该销地的总需要量） m n∑ai = ∑ bj （总产量等于总销量） i=1 j=1X≥0 i=1、2、……、m， j=l、2、……、n（运量为非负数）ij的值，便可以得到总运费或运输总吨公里最小的商品运输方案。

毕业设计运用图上作业法
1、绘制交通图根据客户所需货物汇总情况、交通线路、配送点与客户点的布局，绘制出交通示意图。

2、将初始调运方案反映在交通图上任何一张交通图上的线路分布形态无非为成圈与不成圈两类。

对于不成圈的运输，可按“就近调运”的原则即可，很容易得出调运方案。

对于成圈的，可采用破圈法处理，即可得出初始调运方案。

在绘制初始方案交通图时，凡是按顺时针方向调运的货物调运线路，其调运箭头线都画在圈外，称为外圈；否则，其调运箭头线都画在圈内，称为内圈，或者两种箭头相反方向标注也可。

3、检查与调整面对交通图上的初始调运方案，首先分别计算线路的全圈长、内圈长和外圈长（圈长即指里程数），如果内圈长和外圈长都分别小于全圈长的一半，则该方案即为最优方案；否则，即为非最优方案，需要对其进行调整。