当前位置：文档之家 › 图上作业法

图上作业法

  • 格式：ppt
  • 大小：1.57 MB
  • 文档页数：10

下载文档原格式

  / 10

合集下载

图上作业法

图上作业法
《运筹学》第十九讲 2013-8-7
找 奇 点 配 对
CPP问题
配 三 对
《运筹学》第十九讲
2013-8-7
逐 圈 查
CPP问题
就 近


《运筹学》第十九讲 2013-8-7
配 对
《运筹学》第十九讲 2013-8-7
奇 点 就 近
CPP问题

丰5 120 266 石 -6 165 邯 -5 252 郑 7 349
349 郑
3
118 3 393 -5 济 -3 5 青 外圈最小 5 2 317 流量___， 内圈反向 2 流__，消 2 徐 去对流。
2013-8-7
-5
《运筹学》第十九讲
圈 外 Ⅰ圈 五不 调过 半 后
；
外圈长266 内圈长359
5 2 丰 120 266 3
津
石 -3 165 -5 邯
5 252
运输问题图上作业法 5
丰 266 120 德 180 津 石 -3 165 -5 邯 252 6 239 -5
118 393 -5 济 -3 青
317
8
349
郑
2
徐
2013-8-7
《运筹学》第十九讲
找 避 初对 始流 ， 可靠 行右 走 解；
丰台起，顺时针； 5 5
丰 266 120
11

津
石 -3 8 165 -5 邯
2013-8-7
外圈长666; 外圈长? 内圈长____; 丰 550
5
6
圈
266 11
8
120 德
津 6 239 -5
外 圈 三不 过 调 半
圈 Ⅰ Ⅱ Ⅲ

车辆调度方法

车辆调度方法
首先，向北画一条直线，进行逆时针方向“扫描”。这些都是随机 决定的。逆时针旋转该直线，直到装载的货物能装上一辆载重10000件 的卡车，同时又不超载。一旦所有的站点都分派有车辆，就可以利用 “水滴”法安排经过各站点的顺序，图 (b)是所列出的最终的路线设计。
34 图 扫描法设计行车路线
1000
4000
车辆调度方法
图上作业法
——物资调拨
图上作业法
图上作业法的原则可以归纳为： 流向划右方，对流不应当； 里圈、外圈分别算，要求不能过半圈长； 如若超过半圈长，应去运量最小段； 反复运算可得最优方案。
1．运输线路不成圈的图上作业法
对于运输线路不成圈的流向图，只要不出现对流现象，就
是最优调运方案。
2．运输线路成圈的图上作业法
第一步 作出初始方案
A (36) B (23)
C (13)
D
+20 -30
-50
+20
(18)
E
(45)
F
-20
G (29)
I (23) H
(25)
+100
-70
-30
+60
A
B 30
C 20
D
+20 -30
-50
+20
60
E
20
80 F
-20
I 10 -30
H
G
+60 50
9
4
K
0C
8）以B为初始结点，计算与之
相连的点的位势值；
11
6
11 B
9）从剩余位势中选出最小者，
10
D6
标注箭头和位势值；
5

运输线路优化3---图上作业法

运输线路优化3---图上作业法
▪ 按调整后的新方案组织运输，运力消耗为 （20×36+10×23+20×13+30×23+30×25+ 40×18+80×29+20×127）t·km
=8230t·km ▪ 按初始方案组织运输的运力消耗为 （ 20×45+10×23+50×25+80×29+20×127+20 × 13+30×23+60×18）t·km ▪ =9270t·km
2021/5/27
22
❖ 从计算结果看出，里圈流向线长=23km，小于全圈总长 的1/2（85km），没有迂回现象。而外圈流向线长111km ，超过了全圈总长1/2的85km，可以断定，初始运输流向 线路存在迂回现象，所对应的运输方案不是最优方案， 必须进行优化调整。
❖ 第三步 调整初始方案 ❖ 初始运输中，外圈流向线路中运量最小的是A1至B1的
12
二、物流运输线路的选择优化
❖图上作业法的求解规则可以归纳为：流向 划右方，对流不应当；里圈、外圈分别算， 要求不能过半圈长；若超过半圈长，应去 运量最小段；反复运算可得最优方案。
❖图上作业法包括运输线路不成圈的图上作 业法和运输线路成圈的图上作业法。
2021/5/27
13
二、物流运输线路的选择优化
① +7 7
② -2
5
+8
8
③5
④ -8
-8 ⑦
8
-7
2
⑤
⑥ +6 4
+4 ⑧
图3-1 运输线路不成圈的调运方案
做中学
15
2.运输线路成圈的图上作业法
做中学
❖ 对于成圈运输线路的图上作业法，可以按照如下 三个步骤求解，直到寻求到最优方案。成圈的线路 流向图要同时达到既无对流现象，又无迂回现象的 要求才是最优流向图，所对应的方案为最优运输方 案。

图上作业法

图上作业法



当一个调拨方案,即箭头矢量图,画在地图上,若 既无对流,对于任何环路又无迂回,则这一调拨 方案就是最优的。 从任一调拨方案出发,若有对流,则改变分配办 法可以取消对流,若有迂回,则可用缩短外圈或 内圈的箭头矢量长度来取消迂回,经逐步调整, 即可获最佳调拨方案。
图上作业法的基本步骤

1．绘制交通图 根据客户所需货物汇总情况、交通 线路、配送点与客户点的布局，绘制出交通示意图。 2．将初始调运方案反映在交通图上 任何一张交通 图上的线路分布形态无非为成圈与不成圈两类。 对于不成圈的运输，可按“就近调运”的原则即可， 很容易得出调运方案。对于成圈的，可采用破圈法处 理，即可得出初始调运方案。在绘制初始方案交通图 时，凡是按顺时针方向调运的货物调运线路，其调运 箭头线都画在圈外，称为外圈；否则，其调运箭头线 都画在圈内，称为内圈，或者两种箭头相反方向标注 也可。



1.破圈：从距离最大的地方破。 2.配送：就近原则实施配送得初始方案 3.验证:无对流；内圈长与外圈长均小于相应总 圈长的一半，即为合理方案。 4.调整：若不合理，例如内圈长大于总圈长的 一半，则找出内圈上配送最小值，实施内圈配 送值减去此最小值，其余圈内线路加上此最小 值（含外圈及未配送线路）。
3．检查与调整
A330
30 30
B110
40
A140
B330
10 20 20
B440
首先分别计算线路的全 圈长、内圈长和外圈长 （圈长即指里程数）， 如果内圈长和外圈长都 分别小于全圈长的一半， 则该方案即为最优方案； 否则，即为非最优方案， 需要对其进行调整
B220
A230 A3 →B1破圈调运图图
（一）图上作业法 1．绘制交通图 设有A1、A2、A3三个配送点分别有化肥40t、30t、30t，需送往四个客户 点B1、B2、B3、B4，而且已知各配送点和客户点的地理位置及它们之间 的道路通阻情况，可据此制出相应的交通图

表上作业法和图上作业法讲稿

表上作业法和图上作业法讲稿

表上作业法和图上作业法
表上作业法
●定义；表上作业法是指用列表的方法求解线性规划问题中
运输模型的计算方法。

是线性规划一种求解方法。

当某些线性规划问题采用图上作业法难以进行直观求解时，就可以将各元素列成相关表，作为初始方案，然后采用检验数来验证这个方案，否则就要采用闭合回路法、位势法等方法进行调整，直至得到满意的结果。

这种列表求解方法就是表上作业法。

●表上作业法: 建立在运输费用矩阵的求解运输问题的方
法。

表上作业法求解运输问题的思想和单纯形法完全类似：确定一个初始基本可行解——根据最优性判别准则来检查这个基本可行解是不是最优的？
如果是，则计算结束；
如果不是，则进行换基。

——直至求出最优解为止
图上作业法
●定义；图上作业法是将配送运输量任务反应在交通图上，
通过对交通图初始调运方案的调整，求出最优配送车辆运行调度方法。

运用这种方法时，要求交通图上没有货物对流现象，以运行最短路、最低运费或最高行程利用率为优
化目标。

返程或起程空驶的解决方案或措施是:
1) 顺路运输.发布返程或起程空驶信息,寻找搭载.
2) 加收运费; 对单程运输加收运费.
3) 建立联系; 与相关单位或同业建立互通有无的合作关系,联合行动。

运输管理决策--图上作业法与节约里程法

运输管理决策--图上作业法与节约里程法

4
10 10 10 4 J
11）从剩余位势中选出最小者， 标注箭头和位势值；
0 C 11 6 10 6 5 13 A 8 21 H 7 28 I 9 K 10 4 35 11 10 D6 12 G 18 重复计算，可得最优的路线 图，如图所示。
11 B
2 8 E
14 4
F 12
8
10
J 31
4、分送式配送运输
• 由最短距离表，利用节约法计算出 各用户之间的节约里程，编制节约 里程表：
A
A B C D E F G H I
B
16
C
10 14
D
3 7 11
E
0 2 6 7
F
0 0 0 1 8
G
0 0 0 0 0 6
H
6 0 0 0 0 0 6
I
12 6 0 0 0 0 0 8
• 根据节约里程表中节约里程多少的顺序，
Pi
Pj
c
Pi
Pj
a
b
a
b
P0 (1)分别送货
P0 (2)同时送货
最简单的配送方法是利用两辆车分别为Pi、Pj客户配送；此时， 如图1所示，车辆运行距离为D1=2a+2b， 若按图2所示改用一辆车巡回配送，运行距离为D2=a+b+c， 若道路没有什么特殊情况，可以节省车辆运行距离为٥D=（ 2a+2b)—(a+b+c)=a+b—c>0
调整流向
A +20 20 B -30 10 C -50 20 D +20 E F +100 -20
40
80 H 30 G
I
30

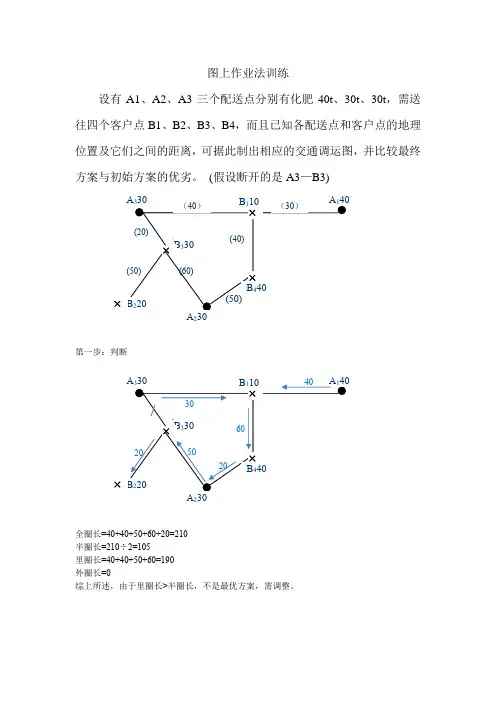
图上作业法训练

图上作业法训练

图上作业法训练设有A1、A2、A3三个配送点分别有化肥40t 、30t 、30t ，需送往四个客户点B1、B2、B3、B4，而且已知各配送点和客户点的地理位置及它们之间的距离，可据此制出相应的交通调运图，并比较最终方案与初始方案的优劣。

(假设断开的是A3—B3)第一步：判断全圈长=40+40+50+60+20=210半圈长=210÷2=105里圈长=40+40+50+60=190外圈长=0综上所述，由于里圈长>半圈长，不是最优方案，需调整。

(20)(50) (40) A 330B 110 A 140 B 440B 330B 220A 230（40） （30） (60)(50) × × × × A 330B 110 A 140 B 440B 330 B 220 A 230×× × × 3040 60 50 2020第二步：调整全圈长=40+40+50+60+20=210半圈长=210÷2=105里圈长=40+40+60=140外圈长=20综上所述，由于里圈长>半圈长，不是最优方案，需再调整。

第三步：再调整全圈长=40+40+50+60+20=210半圈长=210÷2=105里圈长=40+60=100外圈长=70综上所诉，外圈长和里圈长都小于半圈长，为最优方案。

A 330B 110 A 140 B 440B 330 B 220A 230××× × 201040 20 40 30 A 330B 110 A 140 B 440B 330 B 220 A 230××× × 3030 20 40 20 10。

表上作业法与图上作业法

表上作业法与图上作业法

例

某建筑公司有三个储砂仓，供应四个拌合场 的混凝土搅拌机所需用砂。各拌合场估计需 砂量合储砂仓的供应能力以及由第i砂仓运往 第j拌合场的单位运价Cij（元/吨）见表。请为 该公司找出一个运费最小的供砂调运方案。
Cij 拌合场
砂仓
B1
0.12 0.09
B2
0.10 0.11
B3
0.08 0.11
物流运输管理
第十一章 管理数学方法在运输组 织中的应用

第一节 表上作业法 第二节 图上作业法 第三节 最短路线问题
第一节 表上作业法

一、数学模型
例1：给出一个物资调运问题，如下表所示， 试用线性规划法求解。
运价 销地
产地
B1
5 1
B2
3 6
B3
10 9
B4
4 6
A1 A2
产量 （ t） 90
200
10
400
10
600
400
供需不平衡的物资调运问题

1、供应量大于需求量
处理：引入一个虚设的需求点，令其的需求量 等于实际问题中供应量与需求量之差。实际中， 相当于在某个供应点的仓库里将多余部分储存 起来了。因此，可视其相应运价为 。零

2、需求量大于供应量
处理：引入一个虚设的供应点，令其的供应量等于实 际问题中需求量与供应量之差。实际中，相当于在某 个需求点内设立一个仓库，将不足部分另找出路供应 好，预先储存起来了。相应运价为零。
运价 煤矿
电厂
B1
3 4
B2
5 2
煤产量
5000 11000
A1 A2
A3
需求量
6
10000

运输管理决策 图上作业法与节约里程法

运输管理决策 图上作业法与节约里程法

(0.8)
(0.4)
5
(1.5)
C
D
B
5
4
6
2
4
5
7
8 6 7
6 P
3
5
9
10
(0.6) 7
J
F 3
4
10
(1.5)
5
G 2
(0.6)
9 H
(0.8)
图3-10 第一修正方案
A (0.7)
4 11
8 I (0.5)
6 (1.4)
E
7
F (1.5)
(0.4) D 2
(0.8) C
7 6
P
3 4
5
G
(0.6)
J
9
4
11）从剩余位势中选出最小者， 标注箭头和位势值；
K
0C
12）以A为初始结点，计算与之
11
6
11 B
6
10
D6
12
2
8 E 14
相连的点的位势值； 13）从剩余位势中选出最小者， 标注箭头和位势值；
G 18
5 13 A
8
4 11
10
8 F 12
10）以G为初始结点，计算与之 相连的点的位势值；
于一辆车的额定载重量
? 配送路线确定的原则：成本低、效益高、路线 短、准确性高、劳动消耗少、运力合理等
? 配送路线确定的限制条件：用户对货物品种、 规格、数量的要求；用户对发到时间的要求； 车辆载重量的限制；配送能力的约束等
? 配送路线确定的方法：节约里程法
Pi
Pj
a
b
c
Pi
Pj
a
b

专题二-图上作业法

专题二-图上作业法

• 某公司每年要购入1200台 X 产品。供应商的条件 是： 1、订货量大于 75 台时，单价 32.50 元； 2、订货量小于 75 台时，单价 35.00 元。 每次订货的费用为 8.00 元；单位产品的年储 存费用为单价的 12% 。 • 试求最优订货批量（40’）
三、ABC分类法
• 某小型企业拥有十项库存品，各库存品的 年需求量、单价如表所示。为了加强库存 品的管理，企业计划采用 ABC库存管理法。 • 假如企业决定按20％的A类物品，30％的B 类物品，50％的C类物品来建立ABC库存分 析系统。问该企业应如何进行ABC分类？
A1 A2 B1 A3 B2 5 2 8 3 1 3 B3 7 A4 5 B4
二、交通线路成圈
例2：有某物资7万吨，从A1 、A2 、A3 发出，发量分 别为3、3、1（单位：万吨），收发量平衡，交 通线路如图所示。问：应如何调运，才能使吨公 里数最小？ A3
B4 1 7 4 A1 2 1 3
1
4
B3
3
5 B1 2 4 3 3 B2 3 A2
二、经济订货批量
• 某电子商务企业计划对它的最畅销商品进 行库存分析。这种商品的年需求量为 100000件，单价为100元，年储存成本率 约为单价的20％。该企业的每次订货的成 本是100元。 • 问：经济订货数量是多少? (6分)一年的订 货次数为多少? (3分)两次订货的间隔时间 是多少天? (3分)年库存总成本是多少? (3分)
单位产品的年储存费用为单价的12试求最优订货批量40三abc分类法某小型企业拥有十项库存品各库存品的年需求量单价如表所示
一、图上作业法
1、线路类型： 单一出发地和单一目的地 多出发地和多目的地 出发地和目的地是同一地点

06 配送_图上作业法

06 配送_图上作业法

20 20
A230
A3 →B1破圈调运图图
B440
B220
60
30
50
B4（40） 50
B2(20)
A2(30)
运距运量交通图
2．将初始调运方案反映在交通图上
A330 20 B330 40 B110 40 40 A140
凡是按顺时针方向调运的货物 调运线路（如A3至B1、B1至B4、 A2至B3），其调运箭头线都画 在圈外，称为外圈；否则，其 调运箭头线（A3至B3）都画在 圈内，称为内圈
06 配送_图上作业法
设有A1、A2、A3三个配送点分别有化肥40t、30t、30t，需送往四个 客户点B1、B2、B3、B4，而且已知各配送点和客户点的地理位置及 它们之间的道路通阻情况，可据此制出相应的交通图 1．绘制交通图
A3（30） 40 B1 （ 10 ） 40 A1（40）
20
B3(30）
20 30 B220 A230
B440
A2 →B4破圈调运图
3．பைடு நூலகம்查与调整
A330 30 B330 10 B110 40 30 A140
首先分别计算线路的全 圈长、内圈长和外圈长 （圈长即指里程数）， 如果内圈长和外圈长都 分别小于全圈长的一半， 则该方案即为最优方案； 否则，即为非最优方案， 需要对其进行调整

模块三 物资调运问题的图上作业法

模块三 物资调运问题的图上作业法
无圈流向图是否最优判定定理：只要无圈流向图中没 有对流，就一定是最优的。 （有无对流）
【例3.1】求不成圈问题的最优调运方案
A1 100 100
A2 20
50 80
B1 140
60
80
B3
A3 60 20
B2
20
120
100
140
100
A4
B4
案例分析
第一步：编制货物产销平衡表；
表3-1
货物产销平衡表
对应的线路长度或运价； ▼距离或运价写在弧的旁边
§物资调运流向图的一些规定：
1、箭头方向表示物资运输的方向（流向）； 2、带箭头直线（流向）画在A到B前进方向的右侧 ； 3、运输物资的数量（流量）写在箭头线的旁边，加
小括号。 4、流向不能直接跨越路线上的收点、发点、交叉点 5、同一段线路上的多条流向必须合并。即任何一段
▼一是有发点（产地）和收点（销地） ； ▼二是有发点的发量及收点的收量； ▼产地（发点）用“○”表示，产量写在圆圈内 ▼销地（收点）用“□”表示，销量写在方框内 ▼三是有连接收点、发点的交通线路以及与之相
对应的线路长度或运价； ▼距离或运价写在弧的旁边
如何绘制交通路线图呢？
• 交通路线图的绘制：
• 第一步是先标出产地（发点）和销地（收点），产地“○” 内填上该产地的产量（发量)；销地“□” 内填上该销地的 销量(收量)。
(20)
甲 20
10
10 乙
(10)
图 4-4
经检验：初始方案中无对流现象，故方案为最优！
第四步：得到最优调运方案1
表3.2 货物最佳调运方案
销地（收点）
B1
产地（发点）
B2

规划商品运输方案的图上作业法

规划商品运输方案的图上作业法

规划商品运输方案的数学方法合理地规划产销联系是实现商品合理运输的重要手段之一。

商品产销联系规划，实质上就是为各种商品规化最有利的供应范围和流通路径，把生产地和销售地之间的联系具体化。

因此合理规划产销联系的基本原则是：在满足需要的前提下，使商品的运输费用最小或运输吨公里最少。

1．运输问题的数学模型假如某运输企业，要将某种商品从m 个产地，即A 1、A 2、……、A m ；运往n 个销售地，即B 1、B 2、……、B n 已知产地A i （i=l 、2、……、m ）的发运量为a i （i=1、2、……、m ），销售地B j （j=1、2、……、n ）的需要量为b j （j=1、2、……、n ）。

并且每个生产地到各售地的单位运价为C ij （i=1、2、……、m ，；j=1、2、……、n ）；运输距离为 L ij （i=1、2、……、m ，j=l 、2、……、n ）。

问应如何规划运输方案，是总的运费最低或运输吨公里最小？ 在此仅讨论产销平衡问题的数学模型。

当产销平衡时，总的生产量=总的销售量； 单位运价=C ij假设从生产地Ai 运往销售地Bj 的商品数量为Xij （i=1、2、……、m ，j=l 、2、…… 、n ），当目标函数为最小运输费用时，目标函数可表示为： Smin =C 11X 11+…+C 1n ·X 1n +C 21·X 21…+C 2n ·X 2n +…+C m1·X m1+…Cmn·Xmnm n= ∑ ∑ C ij ·X ij j=1 i=1同理，当目标函数为总运输吨公里最小时，目标函数可表示为：m nSmin = ∑ ∑ L ij ·X ij j=1 i=1约束条件为：n∑ X ij =ai ，i=l 、2、……、mj=1（表示从每个产地运往各个销地的商品数量之和，即等于此产地的总产量）m∑ X ij =bj ，j=l 、2、……、n i=1（表示从各个产地运到某个销地的商品数量之和，即等于该销地的总需要量） m n∑ai = ∑ bj （总产量等于总销量） i=1 j=1X≥0 i=1、2、……、m， j=l、2、……、n（运量为非负数）ij的值，便可以得到总运费或运输总吨公里最小的商品运输方案。

奇偶点图上作业法

奇偶点图上作业法

奇偶点图上作业法奇偶点图作业法(graphical method based on an odd-even-point approach)是求最优邮递路线的一种方法。

方法介绍其特点是:对有奇点的街道，方法是求邮递员递送邮件的路线为最短.设在某条路线中的边w, , v;〕上重复走了几次，在v;,v，之间增加几条边，令每条边的权和原来的权相等，并把新增加的边称为重复边.这样，就把原问题变为:在一个有奇点的图中，要求增加一些重复边，使新图不含奇点，并且重复边的总权为最小.把使新图不含奇点而增加的重复边，简称可行(重复边)方案.使总权最小的可行方案称为最优方案。

转变方法1.第一个可行方案的确定方法.若图中有奇点，则把它配成对，每一对奇点之间必有一条链，把这条链的所有边作为重复边加到图中去，新图中必无奇点.便给出了第一个可行方案.2.调整可行方案，使重复边总长度下降.当边w,,v;]上有两条或两条以上的重复边时，从中去掉偶数条，得到一个总长度较小的方案.于是，有:1)在最优方案中，图的每条边上最多有一条重复边.2)在最优方案中，图中每个圈上的重复边的总权不大于该圈总权的一半.3.判断最优方案的标准一个最优方案一定是满足上述1)和2)的可行方案.反之，一个可行方案若满足上述1)和2)，则这个可行方案一定是最优方案.根据判断标准，对给定的可行方案，检查它是否满足上述条件1)和2).若满足，所得方案即为最优方案;若不满足，则对方案进行调整，直至上述条件1)和2)均得到满足时为止.例子：求图 G 的最优环游①配对图 G 中有 6 个奇点 v2,v4,v5,v7,v9,v10 ，把它们配成三对： v2 与 v5 ， v4 与 v7 ， v9 与 v10 。

②添加重边，去掉奇点在图 G 中，取一条连接 v2 与 v5 的路 v2v3v4v5 ，把边 (v2,v3) , (v3,v4) , (v4,v5) 作为重复边加入图中；再取 v4 与 v7 之间一条路 v4v5v6v7 ，把边 (v4,v5) , (v5,v6) ， (v6,v7) 作为重复边加入图中；最后在 v9 和 v10 之间加一条重复边 (v9,v10) ，则图中没有奇点，是一个欧拉图。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第二节 图上作业法
一、图上作业法的基本知识
1.图上作业法的常用符号 2.线形分类
二、交通图不含圈的图上作业法
三、交通图含圈的图上作业法
主题思路
一、运输路线图上作业法的的定义、适用范围 二、编制并解释交通图和流向图 三、内圈流向、外圈流向举例 四、不合理的现象（对流、迂回） 五、案例分析 六、技能训练解析
新的流量图中，在A1B1B2A3B4圈内，内流长4+7=11km，外 流长5km，都不超过新圈长（23km）的一半。在B2A2B3A4圈内，内 流长为3km，外流长为4+2=6km，也都没有全圈（13km）的一半， 因此，这个流向图没有迂回现象，是该问题的最优调运方案。此 时，按调整后的新方案组织运输，总运输量为：
外圈的最小流量1万吨，然后在内圈的各流量中加上1万吨，在此圈
中，因无内流量，所以无处可加。另外，在无流量的线段上，新添
上内圈流量1万吨，这样得出新的流量图。如图3-8所示.
B4
A3
1
（3）
1
（4）
1 B3
（7）
1 3
（5）
2
2
BI
（4）
1 （4）
（2）
1
2
3
3 A2
（3）
B2
图3-8
检验新运输线路图中的里外圈流向长，看是否超过全圈（封 闭回路线）总长的1/2.
图上作业法的适用范围
B4
1
（7）
3
A1
A3
（3）
1
（4）
（4）
1
B3
（2）
（5）
2
BI
3
（4）
B2
（3）
3 A2
注：
表示接收点，其中数字表示运入量。
表示发运点，其中数字表示发运量。
（ ） 中数字表示两地距离。
图3-6
步骤一 去线破圈
作一个没有对流的流向图，用“去线破圈”的方法，去一线破一圈， 有几个圈去掉几个线，把有圈的交通图化成不成圈的交通图。一般是先去掉最 长的交通线，如去掉A1B4（7km），破A1B1B2A3B4圈。再去掉A3B3（4km），破 B2A2B3A4圈，原来有圈的交通图，变成了不成圈的交通图，如图3-7所示。
里)。
不合理的现象2：迂回
（2）迂回：当收点与发点之间的运输线路有两条
或两条以上时（即交通图成圈），如果运送的货 物不是走最短线路，则称这种运输为迂回运输。
注：当交通图成圈时，如果流向图中内圈流向的总 长（简称内圈长）或外圈流向的总长（简称外圈 长）超过整个圈长的一半就称为迂回运输。例如 某物资流向图如图4-6、4-7所示。
（1）对流：所谓对流就是在一段线路上有同一种物资出现相对
运输现象（往返运输）（同一段线路上，两各方向都 有流向），如图4-4。
(20)
(10)
(20)
甲 20
10
10 乙
甲 20
10 10 乙
(10)
(10)
图 4-4
图 4-5
•甲乙两地是一种对流现象。如果把流向图改成图4-5，就
可以避免对流现象，从而可以节约运输量20×10=200(吨公
再看看B2A2B3A4 ，其总长为13km，圈中内流向长为3km，外流向为 2km,都小于圈长的一半，因此此圈不必调整。
步骤三 重新去段破圈，调整流向。
初始方案中圈A1B1B2A3B4 的里圈符合要求，外圈流向超过 全圈总长的一半，故需缩小外圈。
对圈A1B1B2A3B4 的调整方法是，在外圈的各流量中，减去
顺时针方向的流向必须画在圈的内侧，称为内圈流向 逆时针方向的流向必须画在圈的外侧，称为外圈流向
内圈流向、外圈流向举例
图：4-6
6
图：4-7
6
（4）
4
4
4
4
2
顺时针方向的流 向必须画在圈的内侧， 称为内圈流向。如图： 4-6
2
（4）
逆时针方向 的流向必须画在圈的 外侧，称为外圈流向。 如图：4-7
1×7+2×5+1×4+2×3+2×1=29(t.km)
• 初始方案组织运输的运输量为：
（t.km）
3×5+1×4+3×2+2×1+3×1=30
技能训练
某企业由甲、乙、丙3个工厂，产品销往A、
B、C、D、E、F、G、H八个地区。各工厂的位置、
迂回运输的判断
6 （4）
4
4
2 图：4-6
显然：图4-6为迂回运输
6
4
4
2 （4）
图：4-7
正规（最优）流向图：
一个最优的调运方案，它的流向图必是无 对流、无迂回的流向图，称这种流向 为正规流向图。 物资调运的图上作业法就是寻找一个无对流、无
迂回的正规流向图。 步骤如下：
作出一个无对流的初始可行方案； 检验有无迂回； 若无，结束； 否则，调整，直到最优。
交通图
反映发点（产地）与收地（销地）及交通线路及其距离组成的 图形。
发点用“○”表示，发出货物的数量记在“○”之内（单位： 吨）
收地（销地）用“□”表示，收取货物的数量记在“□”之内 （单位：吨）
两点之间的线路长度记在交通线路的旁边。
10
A 3
B
D 39 C
F8
5 2
5
2
7 G
49 E
含有圈的流向图的补充规定
案例分析
（一）任务内容
有某物资7万吨，由发运点A1、A2、A3发出， 发量分别为3、3、1（万吨），运往收点B1、B2、B3， 收收量分别为2、3、1 （万吨），收发量平衡，交通 路线如图3-6所示。问应如何调运，才能使总运输量最 小。 （二）任务目标
掌握成圈与不成圈的图上作业法。 （三）任务准备
然后从各个端点开始，在图上做一个没有对流的流向图。
B4
A3
1
（4）
1
1
1
B3
（7）
ቤተ መጻሕፍቲ ባይዱ（3）
A1 3
（4）
（2） 1
（5）
3
2
（4）
3
1
BI
B2
2 （3）
3 A2 图3-7
步骤二 检验有无迂回
对流向图中的各圈进行检查，看有无迂回。如果没有迂回，这个初始 方案就是最优方案；如果其中某一圈又迂回，这个
方案就不是最优方案，需要改进。
圈A1B1B2A3B4 ：总长为（5+4+4+3+7）=23km
半圈长为（23/2）=11.5km
外圈流向总长为：（5+4+3）=12km
里圈流向总长为 0 km
因为外圈流向总长超过了全圈总长的1/2（12km>11.5km）,可以断定。 圈A1B1B2A3B4初始运输线路存在迂回现象，所对应的运输方案不是最优方案， 因而需要整体优化。
运输路线图上作业法
定义：图上作业法是在运输图上求解线性规划运输模 型的方法。它是在一张运输交通上通过一定步骤的规 划和计算来完成物资调运计划的编制工作，以便使物 资运行的总吨—公里数最小可使物资运费降低，并缩 短了运输时间，所以，在一定条件下称这样的方案为 最优方案。
适用范围：在铁路、公路等交通部门经常使用这种方 法决策最优运输问题。