【初中数学】浙江省温州中学2016年自主招生九年级数学模拟试卷 浙教版

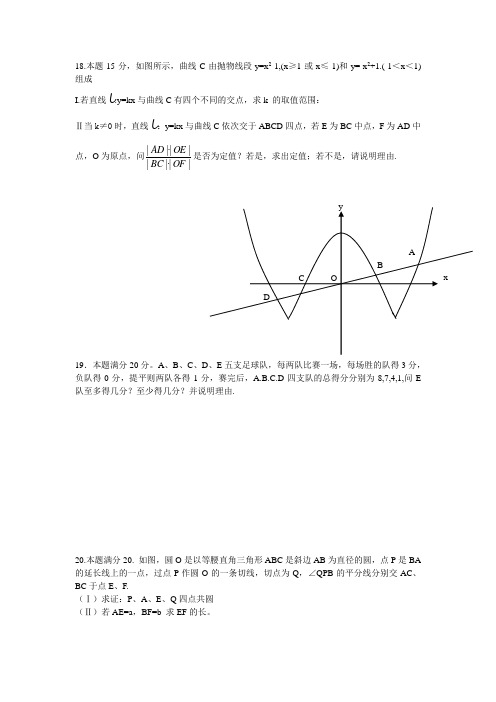
18.本题15分，如图所示，曲线C 由抛物线段y=x 2-1,(x ≥1或x ≤-1)和y=-x 2+1.(-1＜x ＜1)组成
I.若直线l :y=kx 与曲线C 有四个不同的交点，求k 的取值范围：
Ⅱ当k ≠0时，直线l ：y=kx 与曲线C 依次交于ABCD 四点，若E 为BC 中点，F 为AD 中点，O 为原点，问|
|·||||·||OF BC OE AD 是否为定值？若是，求出定值；若不是，请说明理由.
19．本题满分20分。

A 、B 、C 、D 、E 五支足球队，每两队比赛一场，每场胜的队得3分，负队得0分，提平则两队各得1分，赛完后，A.B.C.D 四支队的总得分分别为8,7,4,1,问E 队至多得几分？至少得几分？并说明理由.
20.本题满分20. 如图，圆O 是以等腰直角三角形ABC 是斜边AB 为直径的圆，点P 是BA 的延长线上的一点，过点P 作圆O 的一条切线，切点为Q ，∠QPB 的平分线分别交AC 、BC 于点E 、F.
（Ⅰ）求证：P 、A 、E 、Q 四点共圆
（Ⅱ）若AE=a ，BF=b 求EF 的长。

C
Q P
A B F E。

2016年温州中学提前招生数学测试模拟试题2016年温州中学提前招生数学模拟测试卷考试时间：120分钟满分：150分学校_____________班级_____________姓名___________座位号____________ ………………………………装………………………………订…………………………………线………………………………一、选择题：?x2?x?2?01、关于x 的不等式组?2的整数解只有x??2，则实数k的取值范围是?2x?(2k?5)x?5k?0A、k?2B、?3?k?2C、?3?k?2D、?3?k?22、已知△ABC的两条中线的长分别为5、10。

若第三条中线的长也是整数，则第三条中线长的最大值为。

【出处：21教育名师】A、7B、8C、14D、15 3、有下列四个命题中，真命题的有个。

2①过直线上一点有且只有一条直线垂直于这条直线；②方程x(x?2）?1?0有三个不同的实数解；③非菱形的平行四边形被两条对角线分成了全等的两对三角形，一对是钝角三角形，另一对是锐角三角形；④若二次函数y?x2?ax?a与坐标轴只有一个交点，则a=0或4。

A、0B、1 C、2D、3 4、一条线段AB，绕点A逆时针连续旋转9次，恰好旋转了一周回到原来的位置，如果每一次旋转α°或90－α°，那么α有种可能的取值。

A、4B、6C、8D、10 5、已知平行四边形的对角线交于点O，∠ADC=40°，E是边BC上一点，AD －AB=2BE。

则∠BEO的度数为。

21·cn·jy·com A、140°B、150°C、160°D、165°6、若互不相等的实数a、b、c满足a?2?c?2，b?2?a?2，则b?cc?ac?aa?b等于。

A A、1B、22C、?1D、?22 D7、点D、E分别是等边△ABC的边AB、AC上的点，满足BD=AE，联结CD、BE 交于点O，已知BO=2，CO=5。

（第3题）（第6题） （第2题）永嘉县2016年初中升学考试第一次模拟考试数学试题卷亲爱的同学：欢迎参加考试！请你认真审题，积极思考，细心答题，发挥最佳水平．答题时，请注意以下几点：1． 全卷共4页，有三大题，24小题．全卷满分150分．考试时间120分钟． 2． 答案必须写在答题纸相应的位置上，写在试题卷、草稿纸上均无效． 3． 答题前，认真阅读答题纸上的《注意事项》，按规定答题．祝你成功！卷Ⅰ一、选择题（本题有10小题，每小题4分，共40分．每小题只有一个选项是正确的，不选、 多选、错选，均不给分）1．计算2－3的结果是（ ▲ ）A ．1B ．5C ．－5D ．－12．如图所示的工件的主视图是（ ▲ ）A ．B ．C ．D ．3．如图是某校参加各兴趣小组的学生人数分布扇形统计图，若参加 人数最多的小组是70人，则参加人数最少的小组有（ ▲ ） A ．5人 B ．10人 C ．20人 D ．40人 4．下列选项中的图形，是轴对称图形但不是中心对称图形的是（ ▲ ） A ．平行四边形 B ．正六边形 C ．直角三角形 D ．正三角形 5．在Rt △ABC 中，∠C =90°，AB =2，BC =1，则sin B 的值是（ ▲ ） A ．12B ．2C ．2D ．26．如图，l 1∥l 2∥l 3，直线a ，b 与l 1，l 2，l 3分别相交于点A ，B ，C 和点D ，E ，F ，若32=BC AB ，DE =4，则EF 的长是（ ▲ ）A ．83 B ．203C ．6D ．10 7．不等式组23x x +⎧⎨-⎩≥0＞1的解是（ ▲ ）（第5题）ABA ．x ＜－1B ．x ≥3C ．－1＜x ≤3D ．无解8．某新建火车站站前有一块长为20米，宽为8米的矩形空地，计划在其中修建两块相同的矩形绿地，它们的面积之和为56米2，两块绿地之间及周边留有宽度相等的人行通道（如图所示），则人行通道的宽度是（ ▲ ）A ．1 米B ．2米C ．263米D ．2米或263米9．如图，AB 为⊙O 的直径，点C 为圆上一点，∠BAC =25°，若将劣弧»AC 沿弦AC 翻折交AB 于点D ，连结CD ，则∠DCA 的度数为（ ▲ ）A ．35°B ．40°C ．45°D ．50°10．如图，△AOB 中，点C 为边AB 的中点 ，反比例函数xky =（k ＞0）的图象经过A ，C 两点，若△AOB 的面 积为12，则k 的值是（ ▲ ）A ．8B ．7.5C ．6D ．4卷 II二、填空题（本题有6题，每小题5分，共30分）11．分解因式：x 2－9= ▲ ．12．一个盒子内装有大小、形状相同的四个球，其中红球1个，绿球1个，白球2个，小明摸出一个球不放回，再摸出一个球，则两次都摸到白球的概率是 ▲ ． 13．若扇形的半径为3，扇形的面积为2π，则该扇形的圆心角为 ▲ 度． 14．方程0112=+-xx 的根是 ▲ ． 15．如图，已知点A （2，0），B （0，4），∠AOB 的平分线交AB 于C ，在OA ，OB 上依次取点M ，N ，使得OM =2ON ，设ON =x ， △MNC 的面积为y ，则y 关于x 的函数关系式是 ▲ ．16．如图，已知正方形GFED 的对角线DF 在正方形ABCD 的边DA 上，连结AG ， CE ，并延长CE 交AG 于点H ，若AD =4，DG，则CE 和CH 的长分别（第15题）（第8题）（第9题）（第10题）（第16题）是 ▲ ．三、解答题（本题有8小题，共80分，解答需写出必要的文字说明、演算步骤或证明过程）17．（本题10分）（1）计算：0(2016)313⎛⎫⨯- ⎪⎝-⎭． （2）化简：(x ＋1)2－x (x ＋1)．18．（本题8分）如图，△ABC 与△DCB 中，AC 与BD 交于点O ，且∠A =∠D ，AB =DC ． （1）求证：△ABO ≌△DCO ． （2）当∠AOB =60°，求∠OCB 的度数．19．（本题8分）A ，B ，C 三名学生竞选校学生会主席，他们的笔试成绩和口试成绩（单位：分）分别用了两种方式进行统计，如表一和图一：（1）请将表一和图一中的空缺部分补充完整．（2）竞选的最后一个程序是由本校的300名学生进行投票，A ，B ，C 三位候选人的得票数依次为105，120，75（没有弃权票，每名学生只能推荐一个），若每票计1分，学校将笔试、口试、得票三项测试得分按4:3:3的比例确定个人成绩，请计算三位候选人的最后成绩，并根据成绩判断谁能当选．20．（本题8分）图甲、图乙是两张形状、大小完全相同的6×6方格纸，方格纸中的每个小正方形的边长均为1，点A ，B 在小正方形的顶点上．（1）在图甲中画出一个以点A ，B 为顶点的平行四边形（要求所作的平行四边形不是菱形且各顶点都在格点上），并求出它的周长．（2）在图乙中画出一个以点A ，B 为顶点的菱形（要求所作的菱形各顶点都在格点上），并求出它的面积．（注：图甲、图乙在答题纸上）21．（本题10分）如图，已知△ABC 内接于⊙O ，AB 是⊙O 的直径，点F 在⊙O 上，且满足»BC=»CF ，过点C 作⊙O 的切线交AB 的延长线于点D ，交AF 的延长线于点E ．（1）求证：AE ⊥DE ．（2）若»BC =»CF =60°，AF =4，求CE 的长．（第21题）（第18题）（第19题）22．（本题10分）某蔬菜基地打算将115吨的蔬菜运往县城销售，现找到一物流公司有甲、乙、丙三种车型供选择，每辆车的运载能力和运费如下表所示（假设每辆车均满载，并且每种车型数量足够）：（1）若全部蔬菜都用甲、乙两种车型来运送，需运费7800元，问分别需甲、乙两种车型各几辆？ （2）蔬菜基地计划用甲、乙、丙三种车型共15辆同时参与运送，将全部蔬菜运往县城销售，如何安排装运，可使运费最省？最省运费是多少？23．（本题12分）如图，抛物线223y x x =--+的图象与x 轴交于A ，B 两点（点A 在点B 的左边），与y 轴交于点C ，点D 为抛物线的顶点． （1）求顶点D 的坐标．（2）矩形FMNP 的一边MN 在线段AB 上，点 F ，P 在抛物线上（点F 在点P 的左边），当矩形FMNP 的周长最大 时，求矩形FMNP 的面积．（3）点H 是抛物线上一点，过点H 作y 轴的平行线，与直线AC 交于点E ，交x 轴于点G ． ①若点H 在第二象限内，当HE 最长时，求点H 的坐标． ②连结DH ，当DH =GH 时，请直接写出满足条件的点H 的坐标．24．（本题14分）如图，在Rt △ABC 中，∠ACB =90°，AC =8，BC =6，O 是射线AB 上的一个动点，以点O 为圆心，OA 为半径的⊙O 与射线AC 的另一个交点为D ，直线OD 交直线BC 于点E ． （1）求证：OE =OB ．（2）若AO =4，求CE 的长．（3）设线段BE 的中点为Q ，射线OQ 与⊙O 相交于点P ．①当点E 在线段BC 的延长线上时，若△OBP 的面积 为7.2，求⊙O 的半径．②点O 在运动的过程中，能否使点D ，C ，P ，O 构成 一个平行四边形？若能，请求出AO 的长；若不能， 请说明理由．永嘉县2016年数学中考第一次适应性测试（第23题）（第24题）九年级数学答题卷一、选择题（本题有10小题，每小题4分，共40分）二、填空题（本题有6小题，每小题5分，共30分）11．(x＋3)(x－3)12．1613．8014．x =－2 15．y=－x2＋2x165三、解答题（本题有8小题，共80分）17．（本题10分）（1）原式=1＋(－1) ………………3分=2分（2）原式=x2＋2x＋1－x2－x………………4分=x＋1………………1分18．（本题8分）（1）证明：∵在△ABO和△DCO中AOB DOCABA DDC⎧⎪∠=∠⎨⎪==∠⎩∠，………………3分∴△ABO≌△DCO（AAS）．………………1分（2）解：∵△ABO≌△DCO，∴BO=CO，∴∠OBC=∠OCB，………………2分∵∠OBC＋∠OCB=∠AOB=60°，∴∠OCB=30°．………………2分19．（本题8分）（1）A的口语成绩为90；C的笔试成绩90图略．………………4分（2）A的成绩为4903105385433⨯+⨯+⨯++=92.5（分），B的成绩为4803120395433⨯+⨯+⨯++=98（分），C的成绩为439048533753⨯+⨯+++⨯=84（分），………………3分故B当选．………………1分20．（本题8分）（典型图举例如下：）周长：6面积：8 面积：10 （图形2分，周长2分）（图形2分，面积2分）．21．（本题10分）证明：连结OC，∵OC=OA，∴∠BAC=∠OCA，∵»BC=»CF，∴∠BAC=∠EAC，∴∠EAC=∠OCA，∴OC∥AE，∵DE切⊙O于点C，∴OC⊥DE，∴AE⊥DE．………………5分（2）解：连结OF，∵»BC=»CF=60°，∴∠BAC=∠EAC=30°，∠OAF=∠BAC＋∠EAC=60°，∵OF=OA，∴△OAF为等边三角形，∴OA=AF=4，AB=8，∵AB是⊙O的直径，∴△ABC是直角三角形，∴在Rt△ACB中，AC∵△AEC为直角三角形，∠EAC=30°，∴CE=1AC…………………5分222．（本题10分）（1）设需甲车x辆，乙车y辆，根据题意得∵a ，b ，15－a －b 均为正整数，∴b 只能等于5，10． 设运费为W 元，则W =234007500600855b b b ⎛⎫⎛⎫-++- ⎪ ⎪⎝⎭⎝⎭=207600b -+ ∵k =－20＜0，∴当b =10时，W 取到最小7400．（因此有两种方案；甲，乙，丙分别为5，5，5或3，10，2． 方案一的运费是5×400＋5×500＋5×600=7500（元）， 方案二的运费是3×400＋10×500＋2×600=7400（元），∴甲车3辆，乙车10辆，丙车2辆时，运费最省，最省运费是7400元．） 答：甲车3辆，乙车10辆，丙车2辆时，运费最省，最省运费是7400元．……5分 23．（本题12分） （1） ∵2223(1)4y x x x =--+=-++∴顶点D 的坐标为（－1，4）．…………………………………3分 （2）设F 的坐标为（x ，y ），则2(1)MN x =--．∴矩形周长2224(1)24(1)(23)2822(2)10C =x y =x x x x x =x +--+--+--+--+-+2=．∴当2x =-时，矩形周长最大，此时2(1)2MN x =--=，3NP =．∴矩形面积S =6． …………3分（3）①设H 的坐标为（x ，y ），直线AC ：y=x ＋3．∴23923(3)3()2422HE HG EG x x+x x x x =-=---+=--=-++．∴当32x =-时，HE 最大，此时点H 315,24⎛⎫- ⎪⎝⎭．……3分 ②设H 的坐标为（x ，y ），则G 的坐标为（x ，0），D （-1，4）．当DH=GH 时，此时G 在A 的右侧或G 在B 的左侧，GH=y ，222(1)(4)DH x y =++-∴22222(1)(4)2817y x y x x y y =++-=++-+，即228170x x y +-+=∴291870x x +-=．∴11=3x ，27=3x -，∴点H 72039⎛⎫- ⎪⎝⎭，或12039⎛⎫⎪⎝⎭，．……3分24．（本题14分）（1）证明：∵OA =OD ，∴∠A =∠ODA ，∵∠EDC =∠ODA ，∴∠A =∠EDC ，∵AC⊥BC，∴∠OBE＋∠A=∠OEB＋∠EDC，∴∠OBE=∠OEB，∴OE=OB．………………3分（2）∵∠A=∠EDC，在Rt△ABC和Rt△DEC，sin∠A=BCAB ，sin∠EDC=ECED，∴BC ECAB ED=．Rt△ABC中，∠ACB=90°，AC=8，BC=6，∴AB=10．∵AO=4，∴OB=OE=6，DE=2．∴6102CE=，CE=65．…………4分（3）①如图1，设BE的中点为Q，连结OQ，AO=x ∵OB=OE，∴OQ⊥BE，又∵∠ACB=90°，∴OQ∥AC，∴OB BQAB BC=，∴10106x BQ-=，∴365BQ x=-．………………………2分当△OBP的面积为7.2时，1367.225x x⎛⎫-=⎪⎝⎭．……………………1分解得x1=4，x2=6，即⊙O的半径为4或6．………………………1分②（ⅰ）如果点O在线段AB上，点E在线段BC延长线上时（如图2），由（2）知，∠A=∠EDC，在Rt△ABC和Rt△DEC，cos∠A=ACAB ，cos∠EDC=CDED，∴AC CDAB DE=，∴810102CDx=-，CD=4(102)5x-，当DC=OP时，点D，C，P，O构成一个平行四边形，由DC=OP得，4(102)5x-= x，x=4013．……………………1分（ⅱ）如果点O在线段AB上，点E在线段BC上时（如图3），DC=4(210) 5x-，当DC=OP时，点D，C，P，O构成一个平行四边形，由DC=OP得，4(210)5x-= x，x=403，图1 图2 图3 图4∵403＞10，与点O 在线段AB 上矛盾，∴x =403舍去． ……………………1分 （ⅲ）如果点O 在线段AB 的延长线上（如图4），点E 在线段CB 的延长线上时，DC =4(210)5x -， 当DC =OP 时，点D ，C ，P ，O 构成一个平行四边形， 由DC =OP 得，4(210)5x -= x ，x =403．综上所述，AO =4013或AO =403．……1分16．解：显然△AGD ≅△CED ， ∴∠1＝∠2又∵∠HMA ＝∠DMC ，∴∠AHM =∠ADC ＝90︒．即AG CH ⊥．连结E G ，交AD 于点P ，则GP AD ⊥，由题意有2sin451GP PD =︒=， ∴3AP =，CE = AG = 解法一：∵tan ∠1＝13GP AP =．而∠1＝∠2，∴tan ∠2＝DM DC ＝tan ∠1＝13． ∴43DM =，即83AM AD DM =-=．在Rt DMC ∆中，CM =而AMH ∆∽CMD ∆，∴HM AMDM CM =，即843HM 15HM =∴CH CM MH =+所求CH 的长为5108．解法二：研究四边形ACDG 的面积，而以CD 为底边的三角形CDG 的高=PD =1，M BACDEF G 12 （第16题）HPAGDACDACGCGDACDG SSS SS+==+四边形，∴4×1＋4×CH ＋4 ×1．∴CH =5108．解法三：连结AC ，BD ，交于点O ，则BD 必经过点E ．Rt △COE ∽Rt △CHA ，∴OC CECH AC =， ∴CH ．。

温州市直五校协作体联盟2016届九年级第二次模拟考试数学试卷参考公式：抛物线2(0)y ax bx c a=++≠的顶点坐标为2424b ac ba a⎛⎫-- ⎪⎝⎭，卷Ⅰ一、选择题(本题有10小题，每小题4分，共40分，每小题只有一个选项是正确的，不选、多选、错选，均不给分)1．在数-2，3，0，2中，其中最大的是( ▲)A．-2 B．3C．0 D．22. 某几何体的三视图如图所示，则此几何体是( ▲)A．圆锥B．圆柱C．长方体D．四棱柱3. 计算3a a-+的结果为( ▲)A．a2B．2a-C．4a D．4a-4．如图所示的几何图形中，既是轴对称图形又是中心对称图形的个数是( ▲)A．4 B．3 C．2 D．15. 某校7名初中男生参加引体向上体育测试的成绩分别为：8，5，7，5，8，6，8，则这组数据的众数和中位数分别为( ▲)A．6，7 B．8，7 C．8，6 D．5，76. 分式方程233x x=-的解是( ▲)A．0x=B．3x=C．5x=D．9x=7．已知扇形的弧长为6π，圆心角为120°，则它的半径是( ▲)A．3 B．6 C．9 D．188．不等式组21741xx+>⎧⎨-≥-⎩的解在数轴上表示正确的是( ▲)A．B．C．D．9．如图，已知点A(1,1)关于直线y =kx的对称点恰好落在x轴的正半轴上，则k的值是( ▲)A．12B．21-C．22-D．2210．如图所示，正方形ABCD的顶点B，C在x轴的正半轴(第2题图)(第9题图)上，反比例函数)0(≠=k xky 在第一象限的图象经过顶点A (m ，m +3)和CD 上的点E ，且OB -CE =1，过点E 的 直线l 交 x 轴于点F ，交y 轴于点G （0，-3），则OF 的 长为( ▲ ) A ．4.5B ．5C ．5.4D ．6卷Ⅱ二、 填空题(本题有6小题，每小题5分，共30分) 11．分解因式：92-a = ▲ ．12．已知地球表面陆地面积与海洋面积的比约为3：7.如果宇宙中飞来一块陨石落在地球上，则落在陆地上的概率是 ▲ ．13．如图，AD ∥BE ∥CF ，直线l 1，l 2与这三条平行线分别交于点A ，B ，C 和点D ，E ，F ，23AB BC =，DE =6，则EF = ▲ ．14．如图，⊙O 的直径AB 与弦CD 相交于点E ，AB =5，AC =3，则tan ∠ADC = ▲ ．15. 如图，O 为正方形ABCD 两对角线AC 、BD 的交点，△CDE 为Rt △，∠CED =90°，∠ECD =30°，若正方形ABCD 的边长为4，则OE = ▲ ． 16. 如图，已知抛物线228y x x =-++与x 轴交于点A 、B两点，点C 是这个抛物线上一点且点C 在第一象限，连 接OC 、AC ，点D 是OC 的中点，连结BD 并延长交AC 于点E ．当tan ∠CAB =2时，则△CDE 的面积为 ▲ .(第13题图)(第14题图)(第16题图)(第15题图)三、解答题(本题有8小题，共80分．解答需写出必要的文字说明、演算步骤或证明过程) 17．(本题10分)(1)计算:(2)化简：)1(4)2(2aa---18．(本题8分) 如图，已知：在△AFD和△CEB中，点A，E，F，C在同一直线上，AE=CF，∠B=∠D，AD∥BC，连结DE、BF．(1)求证：△ADF≌△CBE．(2)判断四边形DEBF的形状，并说明理由.19. (本题8分)图1，图2是两张形状、大小完全相同的6×6方格纸，方格纸中的每个小正方形的边长均为1，点A，B在小正方形的顶点上．(1)在图1中画出一个以点A，B为顶点的平行四边形，且面积为6(要求所作的平行四边形各顶点都在格点上)．(2)在图2中画出一个以点A，B为顶点的菱形(要求所作菱形各顶点都在格点上)；20．(本题8分)某私立学校招聘一名数学教师，学校对甲、乙、丙三位候选人进行了三项能力测试，各项测试成绩满分为100分，根据结果择优录用，三位候选人的各项测试成绩如下表所示：(1)如果根据三项测试的平均成绩，谁将被录用，说明理由；(2)根据实际需要，学校将教学、科研、组织三项能力测试得分按5：3：2的比例确定每人的成绩，谁将被录用，说明理由.21．(本题10分)如图，⊙O经过△ABC的顶点A，B，与边AC、BC分别交于点D、E两点，连接BD、AE，且∠ADB =∠CDE(1)求证：△ABE是等腰三角形；(2)若AB =45，BE =8，求⊙O的半径.测试项目测试成绩甲乙丙教学能力85 73 73科研能力70 71 65组织能力64 72 84111224cos302-+-︒+-(第18题图)DOCAB E(第21题图)(第19题图1) (第19题图2)22.(本题10分)楠溪江百丈瀑景区门票价格50元/人，景区为了提高知名度，吸引更多的游客，对门票价格进行动态管 理，非节假日打a 折，节假日期间，10人以下(包括10人) 不打折，10人以上超过10人的部分打b 折，设游客为x 人，门票费用为y 元，非节假日门票费用y 1(元)及节假日 门票费用y 2(元)与游客x (人)之间的函数关系如图所示. (1)a = ▲ ，b = ▲ ；(2)直接写出y 1、y 2与x 之间的函数关系式；(3)导游小胡4月20日(非节假日)带A 旅游团，5月2日(五一劳动节)带B 旅游团到百丈瀑景区旅游，两团共计100人，两次共付门票费用3800元，求A 、B 两个旅游团 各多少人？23．(本题12分)如图，已知抛物线212y x bx c =-++图像经过(-1,4)，且与y 轴交于点 C (0,5).(1)求抛物线的解析式；(2)若P (m ,m +2)是抛物线上位于第一象限内的点，D 是线段 OC 上的一点(不与O 、C 重合)，过点D 分别作DE ∥OP 交CP 于E ，DF ∥CP 交OP 于F . ①求证：四边形DEPF 是矩形；②连接EF ，线段EF 的长是否存在最小值？若存在，求 出EF 的最小值，若不存在，请说明理由.24．(本题14分)已知：如图①，在Rt △ABC 中，∠ACB =90º，AC =15，BC =20，CD ⊥AB ，(第23题图)第22题垂足为D．点E是点D关于AC的对称点，连接AE、CE．(1)求CD和AD的长；(2)若将△ACE沿着射线AB方向平移，设平移的距离为m(平移距离指点A沿AB方向所经过的线段长度)．当点E分别平移到线段AC、BC上时，求m的值．(3)如图②，将△ACE绕点A顺时针旋转一个角α(0°＜α＜180°)，记旋转中的△ACE 为△AC′E′，在旋转过程中，设C′E′所在的直线与直线BC交于点P与直线AB交于点Q．是否存在这样的P、Q两点，使△BPQ为等腰三角形？若存在，求出此时AQ的长；若不存在，请说明理由．图①图②数学答题卷一、选择题(本题有10小题，每小题4分，共40分，每小题只有一个选项是正确的，不选、多选、错选，均不给分)题号 1 2 3 4 5 6 7 8 9 10答案二、填空题（本题有6小题，每小题5分，共30分）11．___________________________ 12．____________________ 13．_______________14．___________________________ 15．____________________ 16．_______________三、解答题（本题有8小题，共80分．解答需写出必要的文字说明、演算步骤或证明过程）17．（1）计算（5分）: （2）化简（5分）：)1(4)2(2aa---18．（8分）(第24题图)111224cos302-+-︒+-(1) (2)19．(本题8分) （1）（2）（第18题(2)）（第18题(1)）（3）23．（本题12分） （1） （2）24.（本题14分）； （1）（第23题）……………………………………………（第24题图1）（2）（3）参考答案一、选择题(本题有10小题，每小题4分，共40分，每小题只有一个选项是正确的，不选、多选、错选，均不给分)1-10、DBACB DCABC二、填空题（本题有6小题，每小题5分，共30分）11．(a+3)(a-3) 12. 0.3 13．914．3415. 26+16.85三、解答题（本题有8小题，共80分．解答需写出必要的文字说明、演算步骤或证明过程）17．（本题10分）(1)计算:=131234222+-⨯+……………(4分)=1 ……………………………………(1分)(2)化简：)1(4)2(2aa---=24444a a a-++-………………(4分)=2a…………………………………(1分)18.(本题8分)（1）∵AD∥BC ∴∠A=∠C ………(1分)∵AE=CF ∴AF=CE …………(1分)（第24题图2）111224cos302--︒+-又∵∠B=∠D∴△AFD≌△CEB(AAS) ………(2分)（2）四边形DEBF为平行四边形……(1分)∵△AFD≌△CEB(AAS)∴DF=EB ∠DFA=∠DEB ……(1分)∴DF平行且等于BE ……(1分)∴四边形DEBF为平行四边形…(1分)19. (本题8分) 如图：其他画法满足条件均得分，（1）（2）小题各4分20．(本题8分)（1）甲的平均成绩为（85+70+64）÷3=73乙的平均成绩为（73+71+72）÷3=72丙的平均成绩为（73+65+84）÷3=74∴丙的平均成绩最好，候选人丙将被录用；………………………(4分) （2）甲的测试成绩为：（85×5+70×3+64×2）÷（5+3+2）=76.3乙的测试成绩为：（73×5+71×3+72×2）÷（5+3+2）=72.2丙的测试成绩为：（73×5+65×3+84×2）÷（5+3+2）=72.8∴甲的平均成绩最好，候选人甲将被录用；………………………(4分)21．(本题10分)（1）证明：∵∠ABE+∠ADE=180°又∵∠CDE+∠ADE=180°∴∠ABE=∠CDE∵∠ADB=∠AEB又∵∠ADB=∠CDE∴∠ABE=∠AEB∴△ABE为等腰三角形………………………(5分)（2）连结AO并延长AO交BE于点F，交⊙O于点G∵AB=AE∴BG=EG∴∠BAF=∠EAF∴AF⊥BE，BF=EF∴AF=84)54(2222=-=-BFAB连结BO，设半径为x，则BO=x,OF=8-xDOCAB E∴2224)8(+-=x x ∴x=5即⊙O 的半径为5 ………………………(5分)22.(本题10分)（1）a = 6 ，b = 8 ；................................(4分)（2）130y x =..........................................(1分)()()2500104010010x x y x x ≤≤⎧⎪=⎨+〉⎪⎩...............................(2分) （3）设B 团有m 人，则A 团的人数为（100-m ）人，当100≤≤m 时，50m +30（100-m ）=3800，解得m =40（不符，舍去）............................(1分)当m>10时，500+40（m -10）+30（100-m ）=3800解得m =70，则100-m =30答：A 团有30人，B 团有70人........................(2分)23．(本题12分)（1）根据题意得：1425b c c⎧=--+⎪⎨⎪=⎩ ...........................(2分) 解得：125b c ⎧=⎪⎨⎪=⎩所以抛物线解析式为211522y x x =-++.....(2分) （2）①把P （m ,m +2）代入211522y x x =-++ 得m =-3（舍去）或m =2得点P 的坐标为（2，4）...............................(2分)∵DE //OP , DF //CP ∴四边形DEPF 是平行四边形.....(1分) 由C (0，5)， P （2，4）可得CP =5, OP =25, OC =5 ∵222CP OP OC += ∴∠CPO =900∴四边形DEPF 是矩形..................................(2分)②存在；连接DP∵四边形DEPF 是矩形 ∴EF =DP当DP ⊥OC 时，DP 最小，∵P （2，4） ∴DP 的最小值是2，∴EF 的最小值是2.....................................(2分)24．(本题14分)（1）CD =12，AD =9；..................... (4分)（2）如图：由对称点性质可知，∠1=∠2由平移性质可知：AC ∥A ′C ′，∠1=∠4 AE=A ′E ′①当点E ′落在AC 上时， ∵AC ∥A ′C ′，∠1=∠2∴∠3=∠4∴∠3=∠2∴AA ′=A ′E ′=9；................ (2分)②当点E ′落在BC 上时，∵AC ∥A ′C ′∴∠6=∠2∵∠1=∠2，∠1=∠5，∴∠5=∠6又易知A ′C ′⊥BC∴△A ′BE ′为等腰三角形，∴A ′B= A ′E ′=9∴AA ′=25-9=16 ................. (2分)顺时针旋转一个角α（0°＜α＜180°）(3).存在，理由如下：在旋转过程，等腰△BPQ 依次有下列4种情形： ①如图1，当PB=BQ 时，得∠2=2∠Q∵∠1=∠3+∠Q ∠1=∠2∴∠3=∠Q ∴△AQC′为等腰三角形 ∴C′Q=AC′=15 ∴E ′Q =12+15=2710927922=+=AQ ................. (2分)②如图2，当PQ=QB 时，得∠P=∠B∵∠C′=∠B ∴∠C′=∠P ∴∠C′=∠P=∠1 可得△AQC′为等腰三角形 ∴C′Q=A Q设AQ 为x ，则C′Q =12-x由勾股定理得：2229(12)x x =+-解得x=758 即AQ=758 ................. (2分)③如图3，当BP=BQ 时，∵∠C′=∠B 可得△AQC′为等腰三角形∴C′Q=AC′=15 ∴QE ′=3∵AE ′=9∴AQ=1039322=+=AQ ............ (1分)④如图4，当BP=PQ时，∵∠C′=∠B可得△AQC′为等腰三角形∴AQ=AC=15 ........... (1分)。

温州中学自主招生模拟试题数学试卷（120分） 一试一. 选择题：本大题共8小题，每小题4分，满分32分。

1. 设0a b >>, 那么21()a b a b +-的最小值是（ ）A.2B.3C.4D.52. 已知一组正数12345,,,,x x x x x 的方差为：222222123451(20)5Sx x x x x =++++-，则关于数据123452,2,2,2,2x x x x x + + + + +的说法：①方差为S2；②平均数为2；③平均数为4；④方差为4S2。

其中正确的说法是（ ）A .①②B .①③C . ②④ D.③④3. 已知实数b a ≠，且满足)1(33)1(2+-=+a a ，2)1(3)1(3+-=+b b .则ba aab b+的值为（ ）A.23B.23-C.2-D.13- 4. 如果x 和y 是非零实数，使得3=+y x 和3=+x y x ，那么x+y 等于（ ）A.3B.13C.2131-D.134-5. 如果对于不小于8的自然数n ，当3n+1是一个完全平方数是，n+1都能表示成个k 完全 平方数的和，那么k 的最小值为（ ） A.1 B.2 C.3 D.46. 已知24b ac -是一元二次方程20ax bx c ++= (a ≠0)的一个实数根，则ab 的取值范围为（ ）A.18ab ≥B.18ab ≤C.14ab ≥D.14ab ≤7. 在四边形ABCD 中，边AB=x ，BC=CD=4, DA=5,它的对角线AC=y ，其中x,y 都是整数，∠BAC=∠DAC,那么，x=( )A.4B.5C.4或5D.非以上答案8. 设二次函数()20y ax bx c a =++≠满足:当01x ≤≤时,1y ≤.则a b c ++的最大值是( ).A.3;B.7;C.12;D.17. 二.填空题：本大题共6小题，每小题5分，满分30分。

9. 在边长为2的正方形A B C D 的四边上分别取点E 、F 、G 、H .四边形E F G H 四边的平方和2222EF FG GH HE +++最小时其面积为_____.10. 已知点A ，B 的坐标分别为（1，0），（2，0）． 若二次函数()233y x a x =+-+的图象与线段AB 恰有一个交点，则a 的取值范围是 ．11. △ABC 中，AB ＝7，BC ＝8，CA ＝9，过△ABC 的内切圆圆心I 作DE ∥BC ，分别与AB ，AC 相交于点D ，E ，则DE 的长为 ．12. 关于x ，y 的方程22208()x y x y +=-的所有正整数解为 ． 13. n 个正整数12na a a ，，，满足如下条件：1212009n a a a =<<<= ；且12na a a ，，，中任意n －1个不同的数的算术平均数都是正整数．则 n 的最大值为___________.14. 如图，射线AM ，BN 都垂直于线段AB ，点E 为AM 上一点，过点A 作BE 的垂线AC 分别交BE ，BN 于点F ，C ，过点C 作AM 的垂线CD ，垂足为D ．若CD ＝CF ，A EA D= ．温州中学自主招生模拟试题数学答题卷（120分） 一试一.选择题：本大题共8小题，每小题4分，满分32分。

浙江省温州中学2016年自主招生九年级数学模拟试卷22016.2（本卷满分：150分 考试时间：90分钟） 注：不得使用计算器及其他任何电子产品一、单项选择题（本大题分5小题，每题4分，共20分）1. 若两个整数x 、y 满足方程(2x +9y )2 006+(4x -y )2 006=7 777777，①就称数组(x ,y )为方程①的一组整数解．则方程①的整数解的组数为··············( )A ．0B ．1C ．2D ．32. 已知点A 、B 分别在x 轴正半轴、y 轴正半轴上移动，4AB =，则以AB 为直径的圆周所扫过的区域面积为·······························( )A ．π4B ．π8C ．42+πD ．46+π3. 若x ∈R +，则93411x x ⎛⎫+- ⎪⎝⎭展开式中常数项为······················( ) A ．-1259 B ．-1260 C ．-1511 D ．-15124. 已知等腰直角ΔPQR 的三个顶点分别在等腰直角ΔABC 的三条边上，记ΔPQR ，ΔABC 的面积分别为S ΔPQR ，S ΔABC ，则PQR ABCS S ∆∆的最小值为··············( ) A ．21 B ．31 C ．41 D ．51 5. 若过点P (1,0)，Q (2,0)，R (4,0)，S (8,0)作四条直线构成一个正方形，则该正方形的面积不可能为·····································( )A ．1716B ．536C ．526D ．53196二、填空题（本大题分10小题，每题6分，共60分）6. 已知a ，b 是不为零的实数，对于任意实数x ，y ，都有()()2222y x b a +++8bx +8ay -k 2+k +28≥0，其中k 是实数，则k 的最大值为 ． 7. 一次考试共有m 道试题，n 个学生参加，其中m ，2≥n 为给定的整数．每道题的得分规则是：若该题恰有x 个学生没有答对，则每个答对该题的学生得x 分，未答对的学生得零分．每个学生的总分为其m 道题的得分总和．将所有学生总分从高到低排列为≥≥21p p …n p ≥，则n p p +1的最大可能值为 ．[用含m ，n 的代数式表示]8. 某情报站有A ，B ，C ，D 四种互不相同的密码，每周使用其中的一种密码，且每周都是从上周未使用的三种密码中等可能地随机选用一种．设第1周使用A 种密码，那么第7周也使用A 种密码的概率是 ．9. 设a 、b 是正整数，且满足⎪⎪⎭⎫ ⎝⎛+b a 15152是正整数．则这样的有序数对(a ,b )共有 对．10. 已知：对任意不小于k 的4个互不相同的实数a ，b ，c ，d ，都存在a ，b ，c ，d 的一个排列p ，q ，r ，s ，使得方程22()()0x px q x rx s ++++=有4个互不相同的实数根．则满足下述条件的最小正实数k 为 ．。

2016年浙江省温州市龙湾区中考数学一模试卷一、选择题（每题4分，共40分）1．给出四个数0，﹣1，，1，其中最大的数是（）A．0 B．﹣1 C．D．12．如图是由五个相同的小立方块搭成的几何体，则它的俯视图是（）A．B．C．D．3．计算（3a2）2的正确结果是（）A．9a5B．6a5C．6a4D．9a44．使分式无意义的x的值是（）A．x=﹣B．x= C．x≠﹣D．x≠5．不等式1﹣x≤0的解在数轴上表示正确的是（）A． B． C． D．6．若关于x的方程x2﹣2x﹣k=0有两个相等的实数根，则k的值为（）A．﹣1 B．0 C．﹣3 D．﹣7．若关于x的方程x2﹣2x﹣k=0有两个相等的实数根，则k的值为（）A．﹣1 B．0 C．﹣3 D．﹣8．如图，已知△ABC（AC＜BC），用尺规在BC上确定一点P，使PA+PB=BC，则下列四种不同方法的作图中，作法正确的是（）A． B．C． D．9．如图，O是坐标原点，菱形OABC的顶点A的坐标为（﹣3，4），顶点C在x轴的负半轴上，函数y=（x＜0）的图象经过顶点B，则k的值为（）A．﹣12 B．﹣27 C．﹣32 D．﹣3610．如图，已知E，F，G，H分别为正方形ABCD各边上的动点，且始终保持AE=BF=CG=DH，点M，N，P，Q分别是EH、EF、FG、HG的中点．当AE从小于BE的变化过程中，若正方形ABCD的周长始终保持不变，则四边形MNPQ的面积变化情况是（）A．一直增大 B．一直减小 C．先增大后减小 D．先减小后增大二、填空题（本题共6小题，每小题5分，共30分）11．分解因式：a2﹣a= ．12．方程=的解是．13．小敏家下个月的开支预算如图所示，如果用于教育的支出是a元，则她家下个月的开支预算总额为元．14．如图，A，B，C三点都在⊙O上，点D是AB延长线上一点，∠AOC=144°，则∠CBD= 度．15．某水果批发商场经销一种高档水果，如果每千克盈利10元，每天可售出500千克，经市场调查发现，在进货价不变的情况下，若每千克涨价1元，日销售量将减少20千克，现该商场要保证每天盈利6000元，设每千克应涨价x元，则可列方程为．16．在一堂关于“折纸问题”的数学综合实践探究课中，小明同学将一张矩形ABCD纸片，按如图进行折叠，分别在BC、AD两边上取两点E，F，使CE=AF，分别以DE，BF为对称轴将△CDE与△ABF翻折得到△C′DE与△A′BF，且边C′E与A′B交于点G，边A′F与C′D交于一点H．已知tan∠EBG=，A′G=6，C′G=1，则矩形纸片ABCD的周长为．三、解答题（本题共8小题，共80分）17．（1）计算：20160++3×（﹣）．（2）化简：（x+1）2﹣2（x﹣2）．18．如图，在方格纸中，A，B，C三点都在小方格的顶点上（每个小方格的边长为1）．（1）在图甲中画一个以A，B，C为其中三个顶点的平行四边形，并求出它的周长．（2）在图乙中画一个经过A，B，C三点的圆，并求出圆的面积．19．一个不透明的袋里装有2个红球，1个白球，1个黄球，它们除颜色外其余都相同．（1）求从袋中摸出一个球是黄球的概率．（2）摸出一个球，记下颜色后不放回，搅拌均匀，再摸出1个球，求两次摸出的球恰好颜色不同的概率（要求画树状图或列表）．20．如图，点A，B，C，D在同一条直线上，点E，F分别在直线AD的两侧，且AE=DF，∠A=∠D，AB=DC．（1）求证：四边形BFCE是平行四边形；（2）若AD=10，DC=3，∠EBD=60°，则BE= 时，四边形BFCE是菱形．21．某工艺品厂设计了一款成本为10元/件的小工艺品投放市场进行试销，经过调查，得到如下数据：销售单价x（元/件）… 20 30 40 50 60…每天销售量y（件）… 500 400 300 200 100…（1）把上表中x，y的各组对应值作为点的坐标，在下面的平面直角坐标系中描出相应的点，猜想y与x的函数关系，并求出函数关系式．（2）当销售单价为多少元时，工艺品厂试销该小工艺品每天获得的利润最大？最大利润是多少？（利润=销售额﹣成本）22．如图，已知直线l与⊙O相离，OA⊥l于点A，交⊙O于点P，OA=5，AB与⊙O相切于点B，BP的延长线交直线l于点C．（1）求证：AB=AC．（2）若PC=2，求⊙O的半径．23．如图，抛物线y=﹣x2+bx+c与x轴分别交于点A（﹣3，0）和点B，与y轴交于点C（0，3），顶点为点D，对称轴DE交x轴于点E，连接AD，AC，DC．（1）求抛物线的函数表达式．（2）判断△ADC的形状，并说明理由．（3）对称轴DE上是否存在点P，使点P到直线AD的距离与到x轴的距离相等？若存在，求出点P的坐标；若不存在，请说明理由．24．已知，如图①，在Rt△ACB中，∠ACB=90°，AC=3，BC=4，点P为线段BC上的一动点（不运动到C，B两点）过点P作PQ⊥BC交AB于点Q，在AC边上取一点D，使QD=QP，连结DP，设CP=x（1）求QP的长，用含x的代数式表示．（2）当x为何值时，△DPQ为直角三角形？（3）记点D关于直线PQ的对称点为点D′．①当点D′落在AB边上时，求x的值；②在①的条件下，如图②，将此时的△DPQ绕点P顺时针旋转一个角度α（0°＜α＜∠DPB），在旋转过程中，设DP所在的直线与直线AB交于点M，与直线AC交于点N，是否存在这样的M，N两点，使△AMN为等腰三角形？若存在，求出此时AN的长；若不存在，请说明理由．2016年浙江省温州市龙湾区中考数学一模试卷参考答案与试题解析一、选择题（每题4分，共40分）1．给出四个数0，﹣1，，1，其中最大的数是（）A．0 B．﹣1 C．D．1【考点】实数大小比较．【分析】根据实数的大小比较，即可解答．【解答】解：∵﹣1＜0＜1＜，∴最大的数是，故选：C．2．如图是由五个相同的小立方块搭成的几何体，则它的俯视图是（）A．B．C．D．【考点】简单组合体的三视图．【分析】找到从上面看所得到的图形即可，注意所有的看到的棱都应表现在俯视图中．【解答】解：从上面看易得上面一层有3个正方形，下面中间有一个正方形．故选A．3．计算（3a2）2的正确结果是（）A．9a5B．6a5C．6a4D．9a4【考点】幂的乘方与积的乘方．【分析】根据积的乘方和幂的乘方，即可解答．【解答】解：（3a2）2=32×（a2）2=9a4，故选：D．4．使分式无意义的x的值是（）A．x=﹣B．x= C．x≠﹣D．x≠【考点】分式有意义的条件．【分析】根据分母为0分式无意义求得x的取值范围．【解答】解：根据题意2x﹣1=0，解得x=．故选：B．5．不等式1﹣x≤0的解在数轴上表示正确的是（）A． B． C． D．【考点】在数轴上表示不等式的解集．【分析】求出已知不等式的解集，表示在数轴上即可．【解答】解：不等式1﹣x≤0，解得：x≥1，表示在数轴上，如图所示：故选D6．若关于x的方程x2﹣2x﹣k=0有两个相等的实数根，则k的值为（）A．﹣1 B．0 C．﹣3 D．﹣【考点】根的判别式．【分析】根据方程有两个相等的实数根，得到根的判别式的值等于0，列出关于k的方程，解方程即可得k的值．【解答】解：根据题意得：△=（2）2﹣4×1×（﹣k）=0，即12+4k=0，解得：k=﹣3，故选：C．7．若关于x的方程x2﹣2x﹣k=0有两个相等的实数根，则k的值为（）A．﹣1 B．0 C．﹣3 D．﹣【考点】根的判别式．【分析】根据方程有两个相等的实数根，得到根的判别式的值等于0，解不等式可得k的值．【解答】解：根据题意得：△=（﹣2）2﹣4×1×（﹣k）=0，即12+4k=0，解得：k=﹣3，故选：C．8．如图，已知△ABC（AC＜BC），用尺规在BC上确定一点P，使PA+PB=BC，则下列四种不同方法的作图中，作法正确的是（）A． B．C． D．【考点】作图—复杂作图．【分析】直接利用线段垂直平分线的性质作出AB的垂直平分线进而得出答案．【解答】解：用尺规在BC上确定一点P，使PA+PB=BC，如图所示：，先做出AB的垂直平分线，即可得出AP=PB，即可得出PA+PB=BC．故选：D．9．如图，O是坐标原点，菱形OABC的顶点A的坐标为（﹣3，4），顶点C在x轴的负半轴上，函数y=（x＜0）的图象经过顶点B，则k的值为（）A．﹣12 B．﹣27 C．﹣32 D．﹣36【考点】菱形的性质；反比例函数图象上点的坐标特征．【分析】根据点C的坐标以及菱形的性质求出点B的坐标，然后利用待定系数法求出k的值即可．【解答】解：∵A（﹣3，4），∴OC==5，∵四边形OABC是菱形，∴AO=CB=OC=AB=5，则点B的横坐标为﹣3﹣5=﹣8，故B的坐标为：（﹣8，4），将点B的坐标代入y=得，4=，解得：k=﹣32．故选C．10．如图，已知E，F，G，H分别为正方形ABCD各边上的动点，且始终保持AE=BF=CG=DH，点M，N，P，Q分别是EH、EF、FG、HG的中点．当AE从小于BE的变化过程中，若正方形ABCD的周长始终保持不变，则四边形MNPQ的面积变化情况是（）A．一直增大 B．一直减小 C．先增大后减小 D．先减小后增大【考点】中点四边形．【分析】根据正方形的四条边都相等可得AB=BC=CD=AD，然后求出BE=CF，再利用“边角边”证明△EBF和△FCG全等；可得EF=FG，然后求出∠EFG=90°，同理可得FG=GH=EH，证出四边形EFGH是正方形，同理证出四边形MNPQ是正方形，即可得出结论．【解答】解：在正方形ABCD中，AB=BC=CD=AD，∠A=∠B=∠C=∠D=90°，∵AE=BF=CG=DH，∴AB﹣AE=BC﹣BF，∴BE=CF，在△EBF和△FCG中，，∴△EBF≌△FCG（SAS）；∴∠EFB=∠FGC，EF=FG，∵∠CFG+∠FGC=90°，∴∠CFG+∠EFB=90°，∴∠EFG=180°﹣90°=90°，同理可得：FG=GH=EH，∴四边形EFGH是正方形，同理：四边形MNPQ是正方形，当AE从小于BE的变化过程中，若正方形ABCD的周长始终保持不变，则正方形EFGH先变小后变大，∴四边形MNPQ的面积变化情况是先减小后变大；故选：D．二、填空题（本题共6小题，每小题5分，共30分）11．分解因式：a2﹣a= a（a﹣1）．【考点】因式分解-提公因式法．【分析】这个多项式含有公因式a，分解因式时应先提取公因式．【解答】解：a2﹣a=a（a﹣1）．12．方程=的解是x=6 ．【考点】解分式方程．【分析】分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．【解答】解：去分母得：3x﹣6=2x，解得：x=6，经检验x=6是分式方程的解．故答案为：x=613．小敏家下个月的开支预算如图所示，如果用于教育的支出是a元，则她家下个月的开支预算总额为5a 元．【考点】扇形统计图．【分析】用于教育的支出是a元，所占百分比为1﹣23%﹣33%﹣24%=20%，用教育支出的钱数除以所占的百分比，即可求出支出总额则可求出小敏家下个月的开支预算总额．【解答】解：a÷（1﹣23%﹣33%﹣24%）=a÷20%=5a（元）．答：她家下个月的开支预算总额为5a元．故答案为：5a．14．如图，A，B，C三点都在⊙O上，点D是AB延长线上一点，∠AO C=144°，则∠CBD= 72 度．【考点】圆内接四边形的性质；圆周角定理．【分析】首先在优弧AC上取点E，连接AE，CE，由圆周角定理可求得∠E的度数，又由圆的内接四边形的性质，可得∠CBD=∠E．【解答】解：在优弧AC上取点E，连接AE，CE，∵∠AOC=144°，∴∠E=∠AOC=72°，∵∠ABC=180°﹣∠E，∠ABC=180°﹣∠CBD，∴∠CBD=∠E=72°．故答案为：72°．15．某水果批发商场经销一种高档水果，如果每千克盈利10元，每天可售出500千克，经市场调查发现，在进货价不变的情况下，若每千克涨价1元，日销售量将减少20千克，现该商场要保证每天盈利6000元，设每千克应涨价x元，则可列方程为（10+x）=6000 ．【考点】由实际问题抽象出一元二次方程．【分析】设每千克水果涨了x元，那么就少卖了20x千克，根据市场每天销售这种水果盈利了6 000元可列方程．【解答】解：设每千克水果涨了x元，（10+x）=6000，故答案为：（10+x）=6000．16．在一堂关于“折纸问题”的数学综合实践探究课中，小明同学将一张矩形ABCD纸片，按如图进行折叠，分别在BC、AD两边上取两点E，F，使CE=AF，分别以DE，BF为对称轴将△CDE与△ABF翻折得到△C′DE与△A′BF，且边C′E与A′B交于点G，边A′F与C′D交于一点H．已知tan∠EBG=，A′G=6，C′G=1，则矩形纸片ABCD的周长为62 ．【考点】翻折变换（折叠问题）；矩形的性质；解直角三角形．【分析】延长BA′交CD于M，作MN⊥C′D于N，由矩形的性质得出∠A=∠C=90°，AD=BC，AB=CD，由折叠的性质得出∠C′=∠C=90°，∠A′=∠A=90°，CE=C′E，AB=A′B，∠CDE=∠C′DE，∠CED=∠C′ED，∠ABF=∠A′BF，∠AFB=∠A′FB，由SAS证明△ABF≌△CDE（SAS），得出∠ABF=∠CDE，∠CED=∠AFB，由ASA证明△BEG≌△DFH，得出∠BGE=∠DHF，证出四边形MNC′G是矩形，得出MN=C′G=1，∠GMN=90°，设EG=3x，BG=4x，则BE=5x，CE=C′E=3x+1，CD=AB=A′B=4x+6，由三角函数求出DN=，由勾股定理得出DM=，再由三角函数得出方程，解方程求出x=2，得出AB=CD=14，AD=BC=17，即可得出矩形ABCD的周长．【解答】解：延长BA′交CD于M，作MN⊥C′D于N，如图所示：∵四边形ABCD是矩形，∴∠A=∠C=90°，AD=BC，AB=CD，由折叠的性质得：∠C′=∠C=90°，∠A′=∠A=90°，CE=C′E，AB=A′B，∠CDE=∠C′DE，∠CED=∠C′ED，∠ABF=∠A′BF，∠AFB=∠A′FB，在△ABF和△CDE中，，∴△ABF≌△CDE（SAS），∴∠ABF=∠CDE，∠CED=∠AFB，∴∠BEG=∠DFH，∠EBG=∠FDH，∵CE=AF，∴BE=DF，在△BEG和△DFH中，，∴△BEG≌△DFH（ASA），∴∠BGE=∠DHF，∵∠A′GC′=∠BGE，∠A′HC′=∠DHF，∴∠BGE=∠DHF=∠A′HC′=∠A′GC′=÷2=90°，∴四边形MNC′G是矩形，∴MN=C′G=1，∠GMN=90°，∴∠DMN=∠EBG，∵tan∠EBG=，∴设EG=3x，BG=4x，则BE=5x，∴CE=C′E=3x+1，CD=AB=A′B=4x+6，∵tan∠DMN==tan∠EBG=，MN=1，∴DN=，∴DM=，∵tan∠EBG==，即，解得：x=2，∴AB=CD=14，AD=BC=17，∴矩形ABCD的周长=2×（14+17）=62．故答案为：62．三、解答题（本题共8小题，共80分）17．（1）计算：20160++3×（﹣）．（2）化简：（x+1）2﹣2（x﹣2）．【考点】实数的运算；去括号与添括号；完全平方公式；零指数幂．【分析】（1）原式利用零指数幂法则，算术平方根定义，以及乘法法则计算即可得到结果；（2）原式利用完全平方公式化简，去括号合并即可得到结果．【解答】解：（1）原式=1+2﹣1=2；（2）原式=x2+2x+1﹣2x+4=x2+5．18．如图，在方格纸中，A，B，C三点都在小方格的顶点上（每个小方格的边长为1）．（1）在图甲中画一个以A，B，C为其中三个顶点的平行四边形，并求出它的周长．（2）在图乙中画一个经过A，B，C三点的圆，并求出圆的面积．【考点】作图—应用与设计作图；勾股定理；平行四边形的性质．【分析】（1）根据平行四边形的定义即可求得，由周长公式计算即可得；（2）先确定圆心，再确定半径即可得圆，最后根据圆的面积公式可得答案．【解答】解：（1）如图甲，▱ABCD即为所求作平行四边形，其周长为2（AD+CD）=2（2+4）=12；（2）如图乙，⊙O即为所求作圆，其面积为π•（）2=10π．19．一个不透明的袋里装有2个红球，1个白球，1个黄球，它们除颜色外其余都相同．（1）求从袋中摸出一个球是黄球的概率．（2）摸出一个球，记下颜色后不放回，搅拌均匀，再摸出1个球，求两次摸出的球恰好颜色不同的概率（要求画树状图或列表）．【考点】列表法与树状图法．【分析】（1）直接利用概率公式求解；（2）画树状图展示所有12种等可能的结果数，再找出两次摸出的球恰好颜色不同的结果数，然后根据概率公式求解．【解答】解：（1）从袋中摸出一个球是黄球的概率==；（2）画树状图为：共有12种等可能的结果数，其中两次摸出的球恰好颜色不同的结果数为10，所以两次摸出的球恰好颜色不同的概率==．20．如图，点A，B，C，D在同一条直线上，点E，F分别在直线AD的两侧，且AE=DF，∠A=∠D，AB=DC．（1）求证：四边形BFCE是平行四边形；（2）若AD=10，DC=3，∠EBD=60°，则BE= 4 时，四边形BFCE是菱形．【考点】平行四边形的判定；菱形的判定．【分析】（1）由AE=DF，∠A=∠D，AB=DC，易证得△AEC≌△DFB，即可得BF=EC，∠ACE=∠DBF，且EC∥BF，即可判定四边形BFCE是平行四边形；（2）当四边形BFCE是菱形时，BE=CE，根据菱形的性质即可得到结果．【解答】（1）证明：∵AB=DC，∴AC=DB，在△AEC和△DFB中，∴△AEC≌△DFB（SAS），∴BF=EC，∠ACE=∠DBF∴EC∥BF，∴四边形BFCE是平行四边形；（2）当四边形BFCE是菱形时，BE=CE，∵AD=10，DC=3，AB=CD=3，∴BC=10﹣3﹣3=4，∵∠EBD=60°，∴BE=BC=4，∴当BE=4 时，四边形BFCE是菱形，故答案为：4．21．某工艺品厂设计了一款成本为10元/件的小工艺品投放市场进行试销，经过调查，得到如下数据：销售单价x（元/件）… 20 30 40 50 60…每天销售量y（件）… 500 400 300 200 100…（1）把上表中x，y的各组对应值作为点的坐标，在下面的平面直角坐标系中描出相应的点，猜想y与x的函数关系，并求出函数关系式．（2）当销售单价为多少元时，工艺品厂试销该小工艺品每天获得的利润最大？最大利润是多少？（利润=销售额﹣成本）【考点】二次函数的应用．【分析】（1）将表中各点描在坐标系中，根据点的分别可猜想y与x是一次函数关系，设这个一次函数为y=kx+b（k≠0），根据点的坐标利用待定系数法即可求出该函数关系式式，再验证其余各点是否在该函数关系式的图象上，由此即可得出结论；（2）设工艺品试销每天获得利润为W元，根据“利用=单件利润×销售数量”即可得出W关于x的函数关系式，利用配方法结合二次函数的性质即可解决最值问题．【解答】解：（1）画出图形，如右图所示．由图可猜想y与x是一次函数关系，设这个一次函数为y=kx+b（k≠0），∵这个一次函数的图象经过（20，500），（30，400）两点，∴，解得：，∴函数关系式是y=﹣10x+700．经验证，其他各点也在y=﹣10x+700上．（2）设工艺品试销每天获得利润为W元，由已知得：W=（x﹣10）（﹣10x+700）=﹣10x2+800x﹣7000=﹣10（x﹣40）2+9000，∵﹣10＜0，∴当x=40时，W取最大值，最大值为9000．故：当销售单价为40元时，工艺品厂试销该小工艺品每天获得的利润最大，最大利润是9000元．22．如图，已知直线l与⊙O相离，OA⊥l于点A，交⊙O于点P，OA=5，AB与⊙O相切于点B，BP的延长线交直线l于点C．（1）求证：AB=AC．（2）若PC=2，求⊙O的半径．【考点】切线的性质．【分析】（1）由同圆半径相等和对顶角相等得∠OBP=∠APC，由圆的切线性质和垂直得∠ABP+∠OBP=90°和∠ACB+∠APC=90°，则∠ABP=∠ACB，根据等角对等边得AB=AC；（2）设⊙O的半径为r，分别在Rt△AOB和Rt△ACP中根据勾股定理列等式，并根据AB=AC 得52﹣r2=（2）2﹣（5﹣r）2，求出r的值即可．【解答】证明：（1）连接OB，∵OB=OP，∴∠OPB=∠OBP，∵∠OPB=∠APC，∴∠OBP=∠APC，∵AB与⊙O相切于点B，∴OB⊥AB，∴∠ABO=90°，∴∠ABP+∠OBP=90°，∵OA⊥AC，∴∠OAC=90°，∴∠ACB+∠APC=90°，∴∠ABP=∠ACB，∴AB=AC；（2）设⊙O的半径为r，在Rt△AOB中，AB2=OA2﹣OB2=52﹣r2，在Rt△ACP中，AC2=PC2﹣PA2，AC2=（2）2﹣（5﹣r）2，∵AB=AC，∴52﹣r2=（2）2﹣（5﹣r）2，解得：r=3，则⊙O的半径为3．23．如图，抛物线y=﹣x2+bx+c与x轴分别交于点A（﹣3，0）和点B，与y轴交于点C（0，3），顶点为点D，对称轴DE交x轴于点E，连接AD，AC，DC．（1）求抛物线的函数表达式．（2）判断△ADC的形状，并说明理由．（3）对称轴DE上是否存在点P，使点P到直线AD的距离与到x轴的距离相等？若存在，求出点P的坐标；若不存在，请说明理由．【考点】二次函数综合题．【分析】（1）用待定系数法求出抛物线解析式；（2）先确定出抛物线的顶点坐标，从而求出AD，AC，CD，用勾股定理的逆定理判断即可；（3）先求出∠ADE的正弦值，再分点P在∠DAB的平分线和∠DAB的外角的平分线两种情况用PM=PE建立方程求解即可．【解答】解（1）∵点A（﹣3，0），C（0，3）在抛物线y=﹣x2+bx+c的图象上，∴，∴，∴抛物线解析式为y=﹣x2﹣2x+3，（2）由（1）得抛物线解析式为y=﹣x2﹣2x+3=﹣（x+1）2+4，∴抛物线的顶点D（﹣1，4），∵C（0，3），A（﹣3，0），∴AD=2，AC=3，CD=，∴AD2=AC2+CD2，∴△ADC是直角三角形；（3）存在，理由：∵抛物线解析式为y=﹣x2﹣2x+3=﹣（x+1）2+4，∴E（﹣1，0），∵A（﹣3，0），D（﹣1，4），∴AE=2，DE=4，AD=2，在Rt△ADE中，sin∠ADE==，设P（﹣1，p），∵点P到直线AD的距离与到x轴的距离相等①当点P在∠DAB的角平分线时，如图1，过点P作PM⊥AD，∴PM=PD×sin∠ADE=（4﹣p），PE=p，∵PM=PE，∴（4﹣p）=p，∴p=﹣1，∴P（﹣1，﹣1），②当点P在∠DAB的外角的平分线时，如图2，过点P作PM⊥AD，∴PM=PD×sin∠ADE=（4﹣p），PE=﹣p，∴（4﹣p）=﹣p，∴p=﹣﹣1，∴P（﹣1，﹣﹣1），综上所述，存在点P到AD的距离与到x轴的距离相等，点P（﹣1，﹣1）或（﹣1，﹣﹣1）．24．已知，如图①，在Rt△ACB中，∠ACB=90°，AC=3，BC=4，点P为线段BC上的一动点（不运动到C，B两点）过点P作PQ⊥BC交AB于点Q，在AC边上取一点D，使QD=QP，连结DP，设CP=x（1）求QP的长，用含x的代数式表示．（2）当x为何值时，△DPQ为直角三角形？（3）记点D关于直线PQ的对称点为点D′．①当点D′落在AB边上时，求x的值；②在①的条件下，如图②，将此时的△DPQ绕点P顺时针旋转一个角度α（0°＜α＜∠DPB），在旋转过程中，设DP所在的直线与直线AB交于点M，与直线AC交于点N，是否存在这样的M，N两点，使△AMN为等腰三角形？若存在，求出此时AN的长；若不存在，请说明理由．【考点】几何变换综合题．【分析】（1）由PQ∥AC，得=，列出方程即可解决问题．（2）因为△DPQ为直角三角形，由题意只有∠DQP=90°，如图2中，首先证明四边形PCDQ是正方形，由PQ∥AC，得=，列出方程即可解决问题．（3）①当点D′落在AB边上时，如图3中，设PQ与DD′交于点H．作D于M．由△QHD′∽△ACB，得=，由D′M∥AC，得到=，求出D′M，列出方程即可解决问题．②由题意只有旋转到如图位置时，△AMN是等腰三角形，此时AN=AM．首先证明PA平分∠BAC，再根据△ACP∽△APN，得=，列出方程即可解决问题．【解答】解：（1）如图1中，∵PQ⊥BC，∴∠QPB=∠C=90°，∴PQ∥AC，∴=，∴=，∴PQ=（4﹣x）．（2）因为△DPQ为直角三角形，由题意只有∠DQP=90°，如图2中，∵∠DQP=∠C=∠QPC=90°，∴四边形PCDQ是矩形，∵DQ=PQ，∴四边形PCDQ是正方形，∵∴PQ∥AC，∴=，∴=，∴x=，∴当x=时，△PDQ是直角三角形．（3）①当点D′落在AB边上时，如图3中，设PQ与DD′交于点H．作D于M．∵∠QHD′=∠C=90°，∠HD′Q=∠B，∴△QHD′∽△ACB，∴=，∵D′M∥AC，∴=，∴=，∴D′M=3﹣x，∴QH=PQ﹣PH=3﹣﹣3+x=x，∴=，∴x=．∴x=时，点D′落在AB边上．②由题意只有旋转到如图位置时，△AMN是等腰三角形，此时AN=AM．作PH⊥AB于H，∵PC=，∴PB=BC﹣PC=4﹣=，∵sin∠ABC==，∴=，∴PH=，∴PC=PH，∵PC⊥AC，PH⊥AB，∴PA平分∠BAC，∵AN=AM，∴AP⊥MN，∵∠PAC=∠PAN，∠ACP=∠APN，∴△ACP∽△APN，∴=，∴=，∴AN=．。

温州中学2016年自主招生九年级科学模拟试卷32016.2亲爱的同学：请你认真审题，积极思考，细心答题，发挥最佳水平．祝你成功！1. 答题时，请务必注意以下几点[注：不得使用任何电子产品]：2. 全卷共8页，5大题，32小题．全卷满分150分，考试时间100分钟．3. 可能用到的相对原子质量：H-1C-12N-14O-16Na-23Al-27S-32Cl-35.5K-39Ca-40Mn-55Cu-64I-127 Ba-1374. 可能用到的参考公式：①F=a(加速度)m；② E k(动能)=mv2/2；③v=g(加速度)t [自由落体运动]一、选择题（第1～10题每题3分、第11～13题每题4分且仅1个正确答案，多选、错选、不选均不得分，共42分）1．我国古代劳动人民积累的丰富农业生产经验，至今许多仍在实践中应用．下列叙述与植物激素作用无直接关系的是()．A．适时打顶去心，可促棉株开花结实．(据《农桑辑要》)B．肥田之法，种绿豆最佳，小豆、芝麻次之．(据《齐民要术》)C．正月种白稻，五月收获后，根茬长新稻，九月又成熟．(据《广志》)D．新摘未熟红柿，每篮放木瓜两三枚，得气即发，涩味尽失．(据《格物粗谈》)2．如图为某种植物幼苗(大小、长势相同)均分为甲、乙两组后，在两种不同浓度的KNO3溶液中培养时鲜重的变化情况(其它条件相同且不变)．下列有关叙述，不正确的是()．A．3 h时，两组幼苗均已出现萎蔫现象，直接原因是蒸腾作用和根细胞失水B．6 h时，甲组幼苗因根系开始吸收K+、NO3-，吸水能力增强，使鲜重逐渐提高C．12 h后，若继续培养，甲组幼苗的鲜重可能超过处理前，乙组幼苗将死亡D．实验表明，该植物幼苗对水分和矿质元素的吸收是两个相对独立的过程3．据报道，科学家开发出了利用太阳能分解水的新型催化剂．下列有关水分解过程的能量变化示意图正确的是()．4．如图所示为地磁场磁感线的示意图．在北半球地磁场的竖直分量向下．飞机在我国上空匀速巡航，机翼保持水平，飞行高度不变，由于地磁场的作用，金属机翼上有电势差．设飞行员左方机翼末端处的电势为U1，右方机翼末端处的电势为U2，则( )A．若飞机从西往东飞，U1比U2高B．若飞机从东往西飞，U2比U1高C．若飞机从南往北飞，U1和U2一样高D．若飞机从北往南飞，U1和U2一样高5．两个完全相同的验电器，分别带上不等量的异种电荷，现将它们的金属球用一根绝缘的金属导体接触后分开，则两验电器的金属箔( )A．张角一定都减小，且带上等量异种电荷B．张角一定都增大，且带上等量异种电荷C．张角一定是有一个增大，且带上等量同种电荷D．张角一定是有一个减小，且带上等量同种电荷6．下列实验方案中，不能测定Na2CO3和NaHCO3，混合物中Na2CO3质量分数的是( )A．取a g混合物充分加热，减重b gB．取a g混合物与足量稀盐酸充分反应，加热、蒸干、灼烧，得到b g固体C．取a g混合物与足量稀硫酸充分反应，逸出气体用碱石灰吸收，增重b gD．取a g混合物与足量Ba(OH)2溶液充分反应，过滤、洗涤、烘干，得到b g固体7．晚上，小明挑着一盏不带光源的工艺品小灯笼在家里玩．当把小灯笼移到发光面较大的吸顶灯正下方时(如图甲所示)，会在小灯笼正下方的水平白纸上出现一个影子，关于这个影子的形状，图乙中正确的是( )8．如图所示，有一高为l的平口玻璃杯内装有深度为h的水，上面盖有卡片．现将玻璃杯翻转，水仍能留在玻璃杯内．已知大气压强为p0，水的密度为ρ，假设玻璃杯倒转后卡片稍微凸出，则水的深度变化量Δh近似为()．A． B．C． D．9．一定量的CuS和Cu2S的混合物投入足量的HNO3中，收集到气体V L(标准状况)，向反应后的溶液中(存在Cu2+和SO42-)加入足量NaOH，产生蓝色沉淀，过滤，洗涤，灼烧，得到CuO 12.0 g，若上述气体为NO和NO2的混合物，且体积比为1 : 1，则V可能为()．A．9.0 L B．13.5 L C．15.7 L D．16.8 L10．右图是多用电表欧姆档的原理图，其中电流表的满偏电流为500μA，内阻R g=50 Ω，调零电阻R的最大阻值为30 kΩ，固定电阻R0=50Ω，电池电动势=1.5 V，用它测量电阻R x，能较准确测量的阻值范围是()．A．(1~4)kΩ B．(100~400)Ω C．(10~40)Ω D．(10~40)kΩ11．用个营养级生物的能量、数量构建的金字塔分别称为能量金字塔、数量金字塔．在某一栎林中，第一营养级生物为栎树，第二营养级生物为昆虫，第三营养级生物为蛙、蜥蜴和鸟，第四营养级生物为蛇．该栎林数量金字塔的示意图是()．12．某探究小组用KMnO4酸性溶液与草酸(H2C2O4)溶液反应过程中溶液紫色消失快慢的方法，研究影响反应速率的因素．实验条件作如下限定：所用酸性KMnO4溶液的浓度可选择0.01 mol·L-1、0.001 mol·L-1，催化剂的用量为0.5 g、实验温度为298 K，每次实验KMnO4酸性溶液的用量均为4 mL，H2C2O4溶液(0.1 mol·L-1)的用量均为2 mL．某同学对两种不同浓度的酸性KMnO4溶液进行实验(其它条件相同)，测得如图实验数据(从混合振荡均匀开始计时)：则实验Ⅱ中用KMnO4的浓度变化来表示的平均反应速率为(忽略混合前后溶液的体积变化)()．实验编号溶液褪色所需时间t / min 第1次第2次第3次Ⅰ141311Ⅱ677A．1.0×10-4mol·L-1·min-1 B．1.0×10-3mol·L-1·min-1C．1.5×10-4mol·L-1·min-1 D．无法计算13．已知一足够长的传送带与水平面的倾角为θ，以一定的速度匀速运动．某时刻在传送带适当的位置放上具有一定初速度的物块(如图a 所示)，以此时为t=0时刻纪录了小物块之后在传送带上运动速度随时间的变化关系，如图b所示(图中取沿斜面向上的运动方向为正方向，其中两坐标大小v1＞v2)．已知传送带的速度保持不变．(g取10 m/s2)，则( )图a图bA．0～t1内，物块对传送带做正功B．物块与传送带间的动摩擦因数为μ，μ<tanθC．0～t2内，传送带对物块做功为W=D．系统产生的热量大小一定大于物块动能的变化量大小二、不定项选择题（每题4分且至少有1个正确答案，多选、错选、不选均不得分，少选1个得2分，1个以上不得分，共28分）14．下列各组物质的稀溶液相互反应，无论是前者滴入后者，还是后者滴入前者，反应现象都相同的是()．A．NaHSO4和Ba(OH)2 B．AlCl3和NaOHC．NaAlO2和H2SO4 D．Ba(HCO3)2和Ba(OH)215．如图，在固定斜面上的一物块受到一外力F的作用，F平行于斜面向上．若要物块在斜面上保持静止，F的取值应有一定范围，已知其最大值和最小值分别为F1和F2(F2＞0)．由此可求出( )A．物块的质量 B．斜面的倾角C．物块与斜面间的最大静摩擦力 D．物块对斜面的正压力16．已知2NaAl(OH)4+CO2===2Al(OH)3↓+Na2CO3+H2O．向含2 mol NaOH，1 mol Ba(OH)2，2 mol NaAl(OH)4的混合溶液中慢慢通入CO2，则通入CO2的量和生成沉淀的量关系正确的是()．选项A B C Dn(CO2)mol2346n(沉淀)mol123317．如图所示，电源电动势为E，内阻为r，已知r：R1：R2=1:2:3，电阻值R3=R4，初始时滑动变阻器R的滑片位于中点位置，此时平行金属板中带电质点P处于静止状态．移动滑片，设电压表V1读数变化量的绝对值为，电压表V2读数变化量的绝对值为，电流表A读数变化量的绝对值为ΔI，不考虑电流表和电压表内阻对电路的影响，则()．A．一定大于r B．一定大于rC．滑动变阻器R的滑片由中点逐渐下移的过程中，质点P向下运动且加速度逐渐增大D．滑动变阻器R的滑片处在a点时质点P的加速度值小于处在b点时质点P的加速度18．a、b为截面完全相同的直角楔形物体，分别在垂直于斜边的恒力F1、F2作用下静止在相同的竖直墙面上，如图所示．下列说法正确的是()．A．a、b受力个数一定相等B．F1、F2不一定相等C．a、b所受摩擦力方向一定沿墙面向上D．b受到的摩擦力小于a受到的摩擦力19．如图所示的容器中，A、B各有一个可以自由移动的轻活塞，活塞下是水，上为空气，大气压恒定，A、B底部由带有阀门K的管道相连，整个装置与外界无热交换．开始A中水面比B中高，打开阀门，使A中的水逐渐流向B中，最后达到平衡，在这个过程中()．A、大气压可能对水做功，水的内能增加B、水克服大气压做功，水的内能减少C、大气压可能对水不做功，水的内能不变D、大气压对水不做功，水的内能增加20．如图中a为北极圈，b为晨昏线，P点位于晨昏线的中点．M、N为晨昏线与北极圈的交点，且M、N两点的经度差为90°．若a为昼弧，且P点的纬度为75°N，此时可能为()．A．2月 B．7月 C．9月 D．11月三、简答题（除第24题每空2分外，其余每空均为3分，共25分）21．在如图所示的电路中，各个电阻的阻值已在图中标出，则端点A、B 间的等效电阻为．22．半径为R的匀质半球体置于水平面上，其重心C离球心O点的距离OC=，半球质量为m．在半球的平面上放一质量为的物体，它与半球平面间的静摩擦因数为0.2．则在保持平衡状态的条件下，物体离球心的最大距离为．23．科学兴趣小组的同学取一定量的某碱式碳酸铜晶体[Cu2(OH)2CO3·2H2O]投一定量入水中，后往其中逐滴加入稀盐酸．(1) 某同学通过实验得到沉淀质量、气体质量与加入盐酸的关系如图：当加入60 mL盐酸时的总化学反应方程式为．(2) 若完全反应后产生的气体全部通入100 g 8％的NaOH溶液中充分反应，所得溶液的溶质总质量为．24．长均为L、质量均为m的两根均匀直杆A、B，它们的上端用光滑铰链铰接，悬挂于天花板上，在距离两杆下端点均为处，用光滑铰链M、N与弯杆C铰接A、B两杆被弯杆C撑开的角度为2θ，弯杆C和铰链的质量均不计，如右图所示，则可知弯杆对杆A的作用力方向为，力的大小为．25．质量为M的厚木块静止在光滑水平面上，质量为m的子弹沿水平方向击中木块，当木块被固定时，子弹射入木块的深度为L，若木块不固定，子弹射入木块的深度为用含已知量的式子表示]26．测定人体血液循环量的一种方法是：吸取6.0 mL含放射性元素131I-人血清白蛋白溶液，每1.0 mL含放射性元素碘2.0×10-6 Ci(居里，一种放射性强度的单位)，快速注入静脉中，10 min时抽取1.0 mL静脉血液，测定其中含放射性元素碘为0.0030×10-6 Ci(10分钟内碘的放射性的强度改变可忽略不计)．人的血液循环量为 L；又知碘是甲状腺素的主要成分，健康成人每天适宜摄入量为100 µg~200µg(1µg为10-6g)．为使上述测定结果可靠，从测定人体血液循环量24 h前，连五天服碘化钠(不含放射性碘)50 mg/(5 mL·d)，原因是．四、实验探究题（第27题9分、第28题6分、第29题16分、第30题9分，共40分）27．电压表满偏时通过该表的电流是半偏是通过该表的电流的两倍．某同学利用这一事实测量电压表的内阻(半偏法)实验室提供材料器材如下：待测电压表(量程3V，内阻约为3000欧)，电阻箱R0(最大阻值为99999.9欧)，滑动变阻器R1(最大阻值100欧，额定电压2A)，电源E(电动势6V，内阻不计)，开关两个，导线若干．(1) 虚框内为同学设计的测量电压表内阻电路图的一部分，在答题卷相应位置将其补充完整．(2) 根据设计的电路写出步骤：．(3) 将这种方法测出的电压表内阻记为与内阻的真实值R V先比(填“>”“=”或“<”)R V，主要理由是．28．为验证“镁是植物生活的必需元素”，三位同学进行了实验设计，下列是实验的基本思路．分别指出三个实验思路能否达到实验目的，为什么？(1) 实验一：取生长状况一致的大豆幼苗，用符合实验要求的容器进行培养．对照组容器内只盛有蒸馏水，实验组盛有用蒸馏水配制的镁盐溶液．两组置于相同的适宜条件下培养，并对溶液通气，观察比较两组植物的生长发育情况．(2) 实验二：取生长状况一致的大豆幼苗，栽培在盛有砂性土壤的容器中(砂性土壤肥力均匀，容器符合实验要求)，对照组浇以蒸馏水，实验组浇以蒸馏水配制的镁盐溶液，两组置于相同的适宜条件下培养，观察比较两组植物的生长发育情况．(3) 实验三：取生长状况一致的大豆幼苗，栽培在盛有砂性土壤的容器中(砂性土壤肥力均匀，容器符合实验要求)，对照组浇以含有植物必需的各种元素的完全营养液，实验组浇以不含镁离子的完全营养液，两组置于相同的适宜条件下培养，观察比较两组植物的生长发育情况．答：．29．根据侯德榜制碱法原理并参考下表的数据，实验室制备纯碱Na2CO3的主要步骤是：将配制好的饱和NaCl溶液倒入烧杯中加热，控制温度在30～35℃，搅拌下分批加入研细的NH4HCO3固体，加料完毕后，继续保温30分钟，静置、过滤得NaHCO3晶体．用少量蒸馏水洗涤除去杂质，抽干后，转入蒸发皿中，灼烧2小时，制得Na2CO3固体．四种盐在不同温度下的溶解度(g /100 g水) 表①：＞35℃NH4HCO3会有分解温度0℃10℃20℃30℃40℃50℃60℃100℃溶解度盐NaCl35.735.836.036.336.637.037.339.8 NH4HCO311.915.821.027.0—①———NaHCO3 6.98.19.611.112.714.516.4—NH4Cl29.433.337.241.445.850.455.377.3请回答：(1) 反应温度控制在30～35℃，是因为若高于35℃，则，若低于30℃，则；为控制此温度范围，采取的加热方法为；(2) 加料完毕后，继续保温30分钟，目的是．静置后只析出NaHCO3晶体的原因是．用蒸馏水洗涤NaHCO3晶体的目的是除去杂质(用化学式表示)；(3) 过滤所得的母液中含有(用化学式表示)，需加入，并作进一步处理，使NaCl溶液循环使用，同时可回收NH4Cl；(4) 测试纯碱产品中NaHCO3含量的方法是：准确称取纯碱样品W g，放入锥形瓶中加蒸馏水溶解，加1～2滴酚酞指示剂，用物质的量浓度为c(mol/L)的HCl溶液滴定至溶液由红色到无色(指示CO32-+H+=HCO3-反应的终点)，所用HCl溶液体积为V1mL，再加1～2滴甲基橙指示剂，继续用HCl溶液滴定至溶液由黄变橙，所用HCl溶液体积为V2mL．写出纯碱样品中NaHCO3质量分数的计算式：NaHCO3(%)= ．30．实验室里临时要用NaOH溶液和CO2来制取纯Na2CO3溶液．已知CO2气体通入NaOH溶液过程中极易生成过量NaHCO3，且无明显现象．实验室有下列试剂：①未知浓度的NaOH溶液②37%的盐酸③37%的硫酸④14%盐酸⑤大理石⑥K2CO3固体⑦Cu2(OH)2CO3实验室有下列仪器：铁架台、启普发生器、量筒、烧杯、橡皮管、玻璃导管、分液漏斗．已知下表中各物质在常温时的溶解度(g /100 g水)Na2CO3NaHCO3NaCl Na2SO4NaHSO4NaOH15.98.43535.52040(1) 本实验应选用的仪器除启普发生器、橡皮管、玻璃导管外，还需要．(2) 为保证制得的Na2CO3溶液尽量纯，应选用的药品(填编号)除①外，还需要．(3) 简要叙述实验步骤，直到制得纯Na2CO3溶液(仪器安装可省略)．．(4) 根据给出的溶解度表，若在配制过程中会有晶体析出，则此时NaOH溶液中溶质的质量分数大于．五、分析计算题（第31题5分，第32题10分，共15分）31．把炭和氧化铜组成的混合物隔绝空气加热，充分反应后称量所得剩余固体的质量为112 g，向此剩余固体中加入200 g稀硫酸，稀硫酸恰好被完全反应，过滤后所得滤渣呈红色．同时将反应所得的气体全部通入含溶质37 g的澄清石灰水中，得到沉淀25 g．下列有关说法正确的是()．A．生成气体的质量可能是11克或33克B．滤渣中的红色物质可能是32克或96克C．参与反应的氧化铜质量可能是40克或120克D．稀硫酸的溶质质量可能是38.4克或115.2克32．一水平放置的圆盘绕竖直固定轴转动，在圆盘上沿半径开有一条宽度为2mm的均匀狭缝．将激光器与传感器上下对准，使两者间连线与转轴平行，分别置于圆盘的上下两侧，且可以同步地沿圆盘半径方向匀速移动，传感器接收一个激光信号，并将其输入计算机，经处理后画出相应图线．图(a)为该装置的示意图，图(b)为所接收的光信号随时间变化的图像，横坐标表示时间，纵坐标表示接收到的激光信号强度，图中Δt1＝1.0×10-3s，Δt2＝0.8×10-3s．(1) 激光器和传感器沿半径移动的方向为；作出此判断的理由是．(2) 求图(b)中第三个激光信号的宽度Δt3．2016年温州中学自主招生科学模拟试卷(答题卷)学校 姓名 考号●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●装订线装订线装订线(满分：150分时间：100分钟)[注：不得使用任何电子产品]答案须写在答题纸相应位置上，写在试题卷、草稿纸上均无效．一、选择题（第1～10题每题3分、第11～13题每题4分且仅1个正确答案，多选、错选、不选均不得分，共42分）题12345678910111213目答案题目14151617181920答案二、不定项选择题（每题4分且至少有1个正确答案，多选、错选、不选均不得分，少选1个得2分，1个以上不得分，共28分）三、简答题（除第24题每空2分外，其余每空均为3分，共25分）21. 22.23. (1) (2) 24. 25.26.四、实验探究题（第27题9分、第28题6分、第29题16分、第30题9分，共40分）27. (1)(2分)(2)(5分)(3)(2分) (理由)28. (实验一)，(实验二)，(实验三)，29. (1)(3分)(2)(6分)(3)(4分)(4)(3分)30. (1)(2分) (2)(2分)(3)(3分)(4)(2分)五、分析计算题（第34题5分，第35题10分，共15分）31.(5分)( )32.(10分)(1) (5分)激光器和传感器沿半径移动的方向为；作出此判断的理由是．(2) (5分)2016年温州中学自主招生科学模拟试卷(参考答案)(满分：150分)一、选择题（第1～10题每题3分、第11～13题每题4分且仅1个正确答案，多选、错选、不选均不得分，共42分）题目12345678910111213答案B B B A D C C A A A B D D 二、不定项选择题（每题4分且至少有1个正确答案，多选、错选、不选均不得分，少选1个得2分，1个以上不得分，共28分）题目14151617181920答案AD C AC BCD BD D D三、简答题（除第24题每空2分外，其余每空均为3分，共25分）21. 3Ω 22. 0.6R23. (1) Cu2(OH)2CO3+2HCl=CuCO3↓+CuCl2+2H2O(Cu2(OH)2CO3·2H2O+2HCl=CuCO3↓+CuCl2+4H2O)(2) 13.7g24. 过M水平向左 1.5mg tanθ 25.26. 4 添加碘，避免或减少放射性元素碘被甲状腺吸收四、实验探究题（第27题9分、第28题6分、第29题16分、第30题9分，共40分）27. (1)(2分)(1)实验电路图如图所示(2分)(2)(5分)移动滑动变阻器的滑片，以保证通电后电压表所在之路分压最小(1分)；闭合开关S1、S2，调节R1，使电压表指针满偏(1分)；保持滑动变阻器滑片的位置不变(1分)；断开S2调节电阻箱R0使电压表的指针半偏(1分)；读取电阻箱的电阻值，此即为测得的电压表的内阻(1分)．第27题(3)(2分) > (1分)断开S1调节电阻箱使电压表成半偏状态，电压表所在之路总电阻增大，分得的电压也增大，此时R0两端的电压大于电压表的半偏电压，故>R V(1分，其他合理说法同样给分)．28. (1) (2分)不能．因为蒸馏水和镁盐溶液均缺乏植物必需的矿质元素而使两组植物生长均不正常．(2) (2分)不能．因为两组容器内的砂性土壤中都可能含有镁离子．(3) (2分)不能．因为两组容器内的砂性土壤中都可能含有镁离子．29. (1)(3分)NH4HCO3分解反应速率降低水浴加热(2)(6分)使反应充分进行 NaHCO3溶解度最小 NaCl、NH4Cl、NH4HCO3(3)(4分)NaHCO3、NaCl、NH4Cl、NH4HCO3 HCl(4)(3分)30. (1) (2分)烧杯、量筒(2) (2分)④⑤(3) (3分)①量取一定量的NaOH溶液，分成两等份；②制取CO2，向其中一份NaOH溶液中通入过量的CO2气体；③将两溶液混合均匀．(4) 3.85%五、分析计算题（第34题5分，第35题10分，共15分）31.(5分)( ABC)(多选、错选均不得分，少选1个得3分，少选2个得1分)32.(10分)(1)激光器和探测器沿半径由中心向边缘移动．(2分)理由：由于脉冲宽度在逐渐变窄，表明光信号能通过狭缝的时间逐渐减少，即圆盘上对应探测器所在位置的线速度逐渐增加，因此激光器和探测器沿半径由中心向边缘移动．(3分)(2)设狭缝宽度为d，探测器接收到第i个脉冲时距转轴的距离为，第i个脉冲的宽度，激光器和探测器沿半径的运动速度为v．，，(1分)．(1分)∵，∴，(1分)由此解得：=0.67×10-3s(2分)。

2016年浙江省温州市中考数学模拟试卷一、选择题（（本题有10个小题，每小题4分，共40分）每小题给出的四个选项中，有且只有一个是正确的.请把正确的答案填在答题卡相应的位置．1．给出四个数0，，，﹣4，其中是无理数的是（）A．0 B．C．D．﹣42．为了了解家里的用水情况，以便能更好的节约用水，小方把自己家1至6月份的用水量绘制成如图的折线图，那么小方家这6个月的月用水量最大是（）A．1月B．4月C．5月D．6月3．如图是由五个相同的小立方块搭成的几何体，则它的主视图是（）A．B．C．D．4．要使分式有意义，则m的取值应满足（）A．m≠1 B．m≠﹣1 C．m=1 D．m=﹣15．下列各式计算正确的有（）A．p2•2p3=2p6B．（a+5）2=a2+25 C．D．6．如图，在平面直角坐标系xOy中，已知点A（4，3）和点B（4，0），则sin∠AOB的值等于（）A．B．C．D．7．若是关于x、y的二元一次方程ax﹣3y=1的解，则a的值为（）A．﹣5 B．﹣1 C．2 D．78．不等式组的解集在数轴上表示正确的是（）A．B．C．D．9．如图，矩形OABC的顶点B（7，6），顶点A、C在坐标轴上，矩形内部一点D在双曲线y=上，DE⊥AB于点E，DF⊥BC于点F，若四边形DEBF为正方形，则点D的坐标是（）A．（2，6）B．（3，4）C．（4，3）D．（6，2）10．如图，点C是AB为直径的半圆上一点（O为圆心），以AC、BC为边向上作正方形ACDE和正方形BCFG，点P是DF的中点．若OP=6，AB=10，则△ABC的面积=（）A．10 B．11 C．12 D．13二、填空题：（共6小题，每小题5分，满分30分．）11．分解因式：a2﹣9= ．12．一组数据a，4，3，6，8的平均数为5，则这组数据的中位数是．13．如图，AB∥CD，BD⊥CD，CE平分∠ACD，若∠CAB=100°，则∠CED的度数为度．14．如图，四边形ABCD是⊙O的内接四边形，⊙O的半径为2，∠D=45°，则劣弧AC的长为．15．如图，点E是菱形ABCD的边AB上一点，AB=4，∠DAB=60°，过E的直线EF∥AD交 AC、CD于点P、F，过P的直线GH∥AB交AD、BC于点G、H，设AE的长度为x，鱼形（阴影部分）的面积为y，则y关于x的函数解析式是．16．如图，矩形ABCD中，AB=8，BC=6，E为BC边上一点，且BE=2，F为AB上一点，FG⊥AE分别交AE、CD于点P、G，以PC为直径的圆交线段FG于点Q，若PF=QG，则BF= ．三、解答题（共8小题，满分80分．）解答应写出文字说明，证明过程或推演步骤.17．（1）计算：sin45°+﹣（﹣1）0（2）化简： +．18．请在图甲、图乙所示的方格纸上各画一个面积为6的格点四边形，顶点在格点上．（1）图甲是轴对称但不是中心对称图形（2）图乙是中心对称但不是轴对称图形19．如图，▱ABCD中，点E、F分别是AD、BC的中点，（1）求证：四边形AFCE是平行四边形；（2）若∠BAC=90°，求证：▱AFCE是菱形．20．某调查机构将今年温州市民最关注的热点话题分为消费、教育、环保、反腐及其它共五类．根据最近一次随机调查的相关数据，绘制的统计图表如下：根据以上信息解答下列问题：（1）本次共调查人，请在答题卡上补全条形统计图并标出相应数据；（2）若温州市约有900万人口，请你估计最关注教育问题的人数约为多少万人？（3）在这次调查中，某单位共有甲、乙、丙、丁四人最关注教育问题，现准备从这四人中随机抽取两人进行座谈，求抽取的两人恰好是甲和乙的概率（列数状图或列表说明）．21．如图，点C在以AB为直径的⊙O上，过C作⊙O的切线交AB的延长线于E，AD⊥CE于D，连结AC．（1）求证：AC平分∠BAD．（2）若tan∠CAD=，AD=8，求⊙O直径AB的长．22．今年3月12日植树节，某校组织七、八、九三个年级的部分学生参加植树活动，活动结束后，领队的老师统计各年级学生及植树情况得到如下3条信息：根据信息，解答下列问题：设七年级有x名学生人参加植树活动，三个年级学生共植树y颗．（1）求y关于x的函数解析式；（2）若各年级学生共植树256棵，七年级有多少名学生人参加植树活动；（3）若九年级学生植树数量占总数的百分比不超过50%，求所有学生植树数量的最大值．23．如图，在平面直角坐标系中，抛物线y=x2+bx+c经过点A（8，6）交x负半轴于点B（﹣4，0），直线AB交y轴于C，点P是直线AB下方的抛物线上一动点（不与A、B点重合），过点P作x轴的垂线交直线AB于点Q．（1）求抛物线和直线AB的解析式；（2）设点P的横坐标为m；①用含有m的代数式表示线段PQ的长．②当四边形CDPQ为平行四边形时，求m的值．（3）过点P作PE⊥AB于点E．若PE恰好被x轴平分，则AQ：QE：EB= ．24．如图，A（0，6），B（﹣6，0），点C、D同时从点O、A出发以每秒1个单位的速度分别沿着x轴正半轴和射线AO方向运动，同时点E从点B出发，以每秒2个单位沿着射线BO 运动，过点C的直线l⊥x轴，点F是直线l在x轴上方的一点，且EF=ED，以DE和EF为邻边作菱形DEFG；当点C和点E重合时各点同时停止运动；直线m：y=2x+2交x轴于点M，交y轴于点N；设运动时间为t．（1）如图1直接写出点M和点N的坐标并用t的代数式表示CE和OD的长度．M ，N ，CE= ，OD= ．（2）如图2，当点E在线段OC之间时，证明：菱形DEFG为正方形．（3）在整个运动过程中，①当t的值为多少时，四边形DEFG有一个顶点落在直线m上；②记点D关于直线m的对称点为点D′，当点D′恰好落在直线l上时，直接写出t的值是．2016年浙江省温州市中考数学模拟试卷参考答案与试题解析一、选择题（（本题有10个小题，每小题4分，共40分）每小题给出的四个选项中，有且只有一个是正确的.请把正确的答案填在答题卡相应的位置．1．给出四个数0，，，﹣4，其中是无理数的是（）A．0 B．C．D．﹣4【考点】无理数．【分析】无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．由此即可判定选择项．【解答】解：0，，﹣4是有理数，是无理数，故选：B．2．为了了解家里的用水情况，以便能更好的节约用水，小方把自己家1至6月份的用水量绘制成如图的折线图，那么小方家这6个月的月用水量最大是（）A．1月B．4月C．5月D．6月【考点】折线统计图．【分析】根据折线统计图的特点结合图形即可求解．【解答】解：由统计图可知，小方家这6个月的月用水量最大是15吨，对应月份是4月．故选B．3．如图是由五个相同的小立方块搭成的几何体，则它的主视图是（）A．B．C．D．【考点】简单组合体的三视图．【分析】主视图有3列，每列小正方形数目从左到右分别为1，2，1．【解答】解：主视图是：故选C．4．要使分式有意义，则m的取值应满足（）A．m≠1 B．m≠﹣1 C．m=1 D．m=﹣1【考点】分式有意义的条件．【分析】先根据分式有意义的条件列出关于x的不等式，求出x的取值范围即可．【解答】解：由题意，得1﹣m≠0，解得m≠1，故选：A．5．下列各式计算正确的有（）A．p2•2p3=2p6B．（a+5）2=a2+25 C．D．【考点】分式的加减法；算术平方根；单项式乘单项式；完全平方公式．【分析】根据分式的性质，二次根式的性质，整式的乘法，完全平方公式即可判断．【解答】解：（A）原式=2p5，故A错误；（B）原式=a2+10a+25，故B错误；（D）原式=3﹣2=1，故D错误；故选（C）6．如图，在平面直角坐标系xOy中，已知点A（4，3）和点B（4，0），则sin∠AOB的值等于（）A．B．C．D．【考点】解直角三角形；坐标与图形性质．【分析】根据题意可知：AB⊥x轴，垂足为B，利用勾股定理求出AO的长度后，利用锐角三角函数即可求出答案．【解答】解：∵A（4，3），B（4，0），∴AB⊥x轴，AB=3，由勾股定理可知：AO=5，∴sin∠AOB==，故选（B）7．若是关于x、y的二元一次方程ax﹣3y=1的解，则a的值为（）A．﹣5 B．﹣1 C．2 D．7【考点】二元一次方程的解．【分析】根据题意得，只要把代入ax﹣3y=1中，即可求出a的值．【解答】解：把代入ax﹣3y=1中，∴a﹣3×2=1，a=1+6=7，故选：D，8．不等式组的解集在数轴上表示正确的是（ ）A ．B ．C ．D ．【考点】解一元一次不等式组；在数轴上表示不等式的解集．【分析】先求出每个不等式的解集再求出其公共解集．【解答】解：该不等式组的解集为1＜x ≤2，故选C ．9．如图，矩形OABC 的顶点B （7，6），顶点A 、C 在坐标轴上，矩形内部一点D 在双曲线y=上，DE ⊥AB 于点E ，DF ⊥BC 于点F ，若四边形DEBF 为正方形，则点D 的坐标是（ ）A ．（2，6）B ．（3，4）C ．（4，3）D ．（6，2）【考点】反比例函数图象上点的坐标特征；矩形的性质；正方形的性质．【分析】由点D 在双曲线上可设点D 的坐标为（m ，）（m ＞0），根据点B 的坐标即可得出DE 、DF 的长度，根据正方形的性质即可得出关于m 的分式方程，解之经检验后即可得出结论．【解答】解：∵点D 在双曲线y=上，∴设点D 的坐标为（m ，）（m ＞0），∵B （7，6），∴DE=7﹣m ，DF=6﹣， ∵四边形DEBF 为正方形，∴7﹣m=6﹣，解得：m=4或m=﹣3（舍去），经检验x=4是方程7﹣m=6﹣的解，∴点D的坐标为（4，3）．故选C．10．如图，点C是AB为直径的半圆上一点（O为圆心），以AC、BC为边向上作正方形ACDE和正方形BCFG，点P是DF的中点．若OP=6，AB=10，则△ABC的面积=（）A．10 B．11 C．12 D．13【考点】正方形的性质；勾股定理；圆周角定理．【分析】连接AD、BF，设AC=a，BC=b，首先证明AD+BF=2OP，得a+b=12，再根据a2+b2=100求出ab即可解决问题．【解答】解：如图，连接AD、BF．设AC=a，BC=b，∵AB是直径，∴∠ACB=90°∵四边形ACDE、四边形BCFG都是正方形，∴∠ACD=∠BCF=∠ACB=90°，∴A、C、F共线，B、C、D共线，∴∠DAC=∠BFC=45°，∴AD∥BF，∵DP=PF，AO=OB，∴AD+BF=2PO，∴a+b=12，∴a+b=12，又∵a2+b2=100，∴a2+2ab+b2=144，∴2ab=44，∴S△ABC=ab=11，故选B．二、填空题：（共6小题，每小题5分，满分30分．）11．分解因式：a2﹣9= （a+3）（a﹣3）．【考点】因式分解﹣运用公式法．【分析】直接利用平方差公式分解因式进而得出答案．【解答】解：a2﹣9=（a+3）（a﹣3）．故答案为：（a+3）（a﹣3）．12．一组数据a，4，3，6，8的平均数为5，则这组数据的中位数是 4 ．【考点】中位数；算术平均数．【分析】先根据平均数为5求出a的值，然后根据中位数的概念求解．【解答】解：∵数据6、4、a、3、8的平均数是4，∴=5，解得：a=4，这组数据按照从小到大的顺序排列为：3，4，4，6，8，则中位数为4．故答案为：4．13．如图，AB∥CD，BD⊥CD，CE平分∠ACD，若∠CAB=100°，则∠CED的度数为50 度．【考点】平行线的性质；垂线．【分析】根据两直线平行，同旁内角互补求出∠ACD，再根据角平分线的定义求出∠DCE，然后根据直角三角形两锐角互余列式计算即可得解．【解答】解：∵AB∥CD，∴∠ACD=180°﹣∠CAB=180°﹣100°=80°，∵CE平分∠FCD，∴∠DCE=∠ACD=×80°=40°，∵BD⊥CD，∴∠D=90°，∴∠CED=90°﹣∠DCE=90°﹣40°=50°．故答案为：50．14．如图，四边形ABCD是⊙O的内接四边形，⊙O的半径为2，∠D=45°，则劣弧AC的长为π．【考点】圆内接四边形的性质；弧长的计算．【分析】连接OA、OC，然后根据圆周角定理求得∠AOC的度数，最后根据弧长公式求解．【解答】解：连接OA、OC，∵∠D=45°，∴∠AOC=2∠D=90°，则劣弧AC的长为： =π．故答案为π．15．如图，点E是菱形ABCD的边AB上一点，AB=4，∠DAB=60°，过E的直线EF∥AD交 AC、CD于点P、F，过P的直线GH∥AB交AD、BC于点G、H，设AE的长度为x，鱼形（阴影部分）的面积为y，则y关于x的函数解析式是y=x2﹣4x+8．【考点】菱形的性质．【分析】由菱形ABCD中，直线EF∥AD，直线GH∥AB，易得四边形AEPG是菱形，四边形CHPF 是菱形，然后过点G作GM⊥AE于点M，过点F作FN⊥BC于点N，利用三角形函数求得其高，继而求得答案．【解答】解：∵四边形ABCD是菱形，∴AB∥CD，AD∥BC，∠DAB=∠BAC，∵EF∥AD，GH∥AB，∴AD∥EF∥BC，AB∥GH∥CD，∴四边形AEPG与四边形BCFE是平行四边形，∴∠BAC=∠APG，∴∠DAC=∠APG，∴AG=PG，∴四边形AEPG是菱形，同理：四边形CHPF是菱形，过点G作GM⊥AE于点M，过点F作FN⊥BC于点N，则AG=AE=x，CH=FC=BE=AB﹣AE=4﹣x，∵∠BCD=∠DAB=60°，∴GM=AG•sin60°=x，FN=FC•sin60°=（4﹣x），∴S△PGE=S△AGE=AE•GM=x2，S菱形CHPF=CH•FN=（4﹣x）2，∴y=S阴影=S△PGE+S菱形CHPF=x2﹣4x+8．故答案为：y=x2﹣4x+8．16．如图，矩形ABCD中，AB=8，BC=6，E为BC边上一点，且BE=2，F为AB上一点，FG⊥AE分别交AE、CD于点P、G，以PC为直径的圆交线段FG于点Q，若PF=QG，则BF= ．【考点】相似三角形的判定与性质；矩形的性质；圆周角定理．【分析】连接AC交FG于O，连接PC、CQ，延长AE交PC为直径的圆于H，连接CH．首先证明OA=OC，由△AEB∽△CEH，可得==，推出CH=，EH=，AH=，由OA=OC，OP∥CH，推出AP=PH=，由△APF∽△ABE，可得=，推出AF=，延长即可解决问题．【解答】解：连接AC交FG于O，连接PC、CQ，延长AE交PC为直径的圆于H，连接CH．∵四边形ABCD是矩形，∴AB∥CD，∴∠AFP=∠CGQ，∵PC是直径，∴∠CQP=∠H=90°，∴CQ⊥FG，∵AE⊥FG，∴∠APF=∠CQG=90°，在△APF和△CQG中，，∴△AOF≌△CQG，∴AP=CQ，在△AOP和△COQ中，，∴△AOP≌△COQ，∴OA=OC，在Rt△ABE中，∵AB=8，BE=2，∴AE==2，∵△AEB∽△CEH，∴==，∴CH=，EH=，∴AH=，∵OA=OC，OP∥CH，∴AP=PH=，∵△APF∽△ABE，∴=，∴AF=，∴BF=AB﹣AF=8﹣=，故答案为三、解答题（共8小题，满分80分．）解答应写出文字说明，证明过程或推演步骤.17．（1）计算：sin45°+﹣（﹣1）0（2）化简： +．【考点】分式的加减法；实数的运算；零指数幂；特殊角的三角函数值．【分析】（1）原式利用特殊角的三角函数值，二次根式性质，以及零指数幂法则计算即可得到结果；（2）原式通分并利用同分母分式的加法法则计算即可得到结果．【解答】解：（1）原式=+2﹣1=﹣1；（2）原式=+==．18．请在图甲、图乙所示的方格纸上各画一个面积为6的格点四边形，顶点在格点上．（1）图甲是轴对称但不是中心对称图形（2）图乙是中心对称但不是轴对称图形【考点】作图﹣旋转变换；作图﹣轴对称变换．【分析】（1）根据轴对称的性质画出图形即可；（2）根据中心对称的性质画出图形即可．【解答】解：（1）如图甲所示；（2）如图乙所示．19．如图，▱ABCD中，点E、F分别是AD、BC的中点，（1）求证：四边形AFCE是平行四边形；（2）若∠BAC=90°，求证：▱AFCE是菱形．【考点】菱形的判定；平行四边形的判定与性质．【分析】（1）根据平行四边形的性质可得AD=BC，AD∥BC，再由点E、F分别是AD、BC的中点可得AE=CF且AE∥CF，从而可根据一组对边平行且相等的四边形是平行四边形可得结论；（2）根据直角三角形的性质可得AF=CF，再根据一组邻边相等的平行四边形是菱形可得结论．【解答】证明：（1）在▱ABCD中，∴AD=BC，AD∥BC，∵点E、F分别是AD、BC的中点，∴AE=CF且AE∥CF，∴四边形AFCE是平行四边形；（2）∵∠BAC=90°，点F分别是BC的中点，∴AF=CF，∴▱AFCE是菱形．20．某调查机构将今年温州市民最关注的热点话题分为消费、教育、环保、反腐及其它共五类．根据最近一次随机调查的相关数据，绘制的统计图表如下：根据以上信息解答下列问题：（1）本次共调查1400 人，请在答题卡上补全条形统计图并标出相应数据；（2）若温州市约有900万人口，请你估计最关注教育问题的人数约为多少万人？（3）在这次调查中，某单位共有甲、乙、丙、丁四人最关注教育问题，现准备从这四人中随机抽取两人进行座谈，求抽取的两人恰好是甲和乙的概率（列数状图或列表说明）．【考点】列表法与树状图法；用样本估计总体；统计表；条形统计图．【分析】（1）根据关注消费的人数是420人，所占的比例式是30%，即可求得总人数，然后利用总人数乘以关注教育的比例求得关注教育的人数，进而可补全条形统计图并标出相应数据；（2）利用总人数乘以对应的百分比即可；（3）利用列举法即可求解即可．【解答】解：（1）调查的总人数是：420÷30%=1400（人），关注教育的人数是：1400×25%=350（人）．；（2）900×（1﹣0.3﹣0.1﹣0.15﹣0.2）=225（万）答：估计最关注教育问题的人数约为225万人．（3）画树形图得：则P（抽取的两人恰好是甲和乙）=P=．21．如图，点C在以AB为直径的⊙O上，过C作⊙O的切线交AB的延长线于E，AD⊥CE于D，连结AC．（1）求证：AC平分∠BAD．（2）若tan∠CAD=，AD=8，求⊙O直径AB的长．【考点】切线的性质；解直角三角形．【分析】（1）连接OC，由DE为圆O的切线，得到OC垂直于CD，再由AD垂直于DE，得到AD与OC平行，得到一对内错角相等，根据OA=OC，利用等边对等角得到一对角相等，等量代换即可得证；（2）在直角三角形ADC中，利用锐角三角函数定义求出CD的长，根据勾股定理求出AD的长，由三角形ACD与三角形ABC相似，得到对应边成比例，即可求出AB的长．【解答】证明：（1）连结OC，∵DE是⊙O的切线，∴OC⊥DE，∵AD⊥CE，∴AD∥OC，∵OA=OC，∴∠DAC=∠ACO=∠CAO，∴AC平分∠BAD；（2）解：∵AD⊥CE，tan∠CAD=，AD=8，∴CD=6，∴AC=10，∵AB是⊙O的直径，∴∠ACB=90°=∠D，∵∠DAC=∠CAO，∴△ACD∽△ABC，∴AB：AC=AC：AD，∴AB=．22．今年3月12日植树节，某校组织七、八、九三个年级的部分学生参加植树活动，活动结束后，领队的老师统计各年级学生及植树情况得到如下3条信息：根据信息，解答下列问题：设七年级有x名学生人参加植树活动，三个年级学生共植树y颗．（1）求y关于x的函数解析式；（2）若各年级学生共植树256棵，七年级有多少名学生人参加植树活动；（3）若九年级学生植树数量占总数的百分比不超过50%，求所有学生植树数量的最大值．【考点】一次函数的应用．【分析】（1）根据题意可以写出y关于x的函数解析式；（2）将y=256代入（1）中的函数解析式即可解答本题；（3）根据题意可以列出相应的不等式，从而可以解答本题．【解答】解：（1）由题意可得，y=4x+5×2x+6（50﹣x﹣2x）=300﹣4x，即y关于x的函数解析式是y=300﹣4x；（2）当y=256时，256=300﹣4x，解得，x=11若各年级学生共植树256棵，七年级有11名学生人参加植树活动；（3）由题意可得，6（50﹣x﹣2x）≤×0.5解得，x≥，∵x是正整数，∴x最小=10，∴300﹣4x的最大值是300﹣4×10=260，即学生植树数量的最大值260棵．23．如图，在平面直角坐标系中，抛物线y=x2+bx+c经过点A（8，6）交x负半轴于点B （﹣4，0），直线AB交y轴于C，点P是直线AB下方的抛物线上一动点（不与A、B点重合），过点P作x轴的垂线交直线AB于点Q．（1）求抛物线和直线AB的解析式；（2）设点P的横坐标为m；①用含有m的代数式表示线段PQ的长．②当四边形CDPQ为平行四边形时，求m的值．（3）过点P作PE⊥AB于点E．若PE恰好被x轴平分，则AQ：QE：EB= 15：7：14．．【考点】二次函数综合题；平行四边形的性质．【分析】（1）根据抛物线y=x2+bx+c经过点A（8，6）交x负半轴于点B（﹣4，0），运用待定系数法求得抛物线的解析式，和直线的解析式即可；（2）根据四边形CDPQ为平行四边形，利用PQ=CD，列出方程=，解得：m1=4，m2=0（舍去），即可得到m的值为4；（3）根据抛物线的解析式：，设P（a，b）（﹣4＜a＜8），得到b=①，再根据直线AB的解析式：，得到Q（a， a+2），根据PE⊥AB，得到直线PE的解析式为y=﹣2x+2a+b，再解方程组，可得E的坐标，最后根据PE恰好被x轴平分，得出+b=0②，最后联立①②解方程组可得，求得Q（3，），E（，），进而得到AQ：QE：EB的比值．【解答】解：（1）∵抛物线y=x2+bx+c经过点A（8，6）交x负半轴于点B（﹣4，0），∴，解得，∴抛物线的解析式：，设直线AB的解析式为y=kx+n，则，解得，∴直线AB的解析式：；（2）①∵PQ⊥x轴，点P的横坐标为m，∴P（m， m2﹣m﹣），Q（m，），∴PQ=﹣（）=；②在抛物线中，当x=0时，y=﹣，即D（0，﹣），在直线AB的解析式中，当x=0时，y=2，即C（0，2），∴CD=2﹣（）=∵四边形CDPQ为平行四边形，∴PQ=CD，∴=，解得：m1=4，m2=0（舍去），∴m的值为4；（3）∵抛物线的解析式：，∴设P（a，b）（﹣4＜a＜8），则b=，①∵直线AB的解析式：，∴Q（a， a+2），∵PE⊥AB，∴直线PE的解析式为y=﹣2x+2a+b，解方程组，可得E（，），∵PE恰好被x轴平分，∴+b=0，②联立①②解方程组可得，（舍去），∴Q（3，），E（，），∴AQ：QE：EB=（8﹣3）：（3﹣）：（+4）=15：7：14．故答案为：15：7：14．24．如图，A（0，6），B（﹣6，0），点C、D同时从点O、A出发以每秒1个单位的速度分别沿着x轴正半轴和射线AO方向运动，同时点E从点B出发，以每秒2个单位沿着射线BO 运动，过点C的直线l⊥x轴，点F是直线l在x轴上方的一点，且EF=ED，以DE和EF为邻边作菱形DEFG；当点C和点E重合时各点同时停止运动；直线m：y=2x+2交x轴于点M，交y轴于点N；设运动时间为t．（1）如图1直接写出点M和点N的坐标并用t的代数式表示CE和OD的长度．M （﹣1，0），N （0，2），CE= 6﹣t ，OD= 6﹣t．．（2）如图2，当点E在线段OC之间时，证明：菱形DEFG为正方形．（3）在整个运动过程中，①当t的值为多少时，四边形DEFG有一个顶点落在直线m上；②记点D关于直线m的对称点为点D′，当点D′恰好落在直线l上时，直接写出t的值是．【考点】一次函数综合题．【分析】（1）求出直线y=2x+2与坐标轴的交点，可得M、N点坐标，由题意OE=t，AD=t，BE=2t，可以推出CE、OD的长．（2）根据一个角是90°的菱形是正方形，只要证明∠DEF=90°即可．（3）①分四种情形分别讨论即可．②如图5中，设DD′交直线m于F，作FG⊥OA于G．由△DFG∽△FNG∽△MNO，得===，推出DG=t，GN=t，根据GN=AN﹣AD﹣DG，列出方程即可解决问题．【解答】解：（1）∵y=2x+2交x轴于点M，交y轴于点N，∴M（﹣1，0），N（0，2），由题意，OE=t，AD=t，BE=2t，∴EC=OB+OC﹣BE=6+t﹣2t=6﹣t，OD=OA﹣AD=6﹣t，故答案为（﹣1，0），（0，2），6﹣t，6﹣t，（2）证明：点E在线段OC之间∵CE=6﹣t=OD，EF=ED，∠DOE=∠ECF=90°．∴△DOE≌△ECF∴∠DEO=∠EFC∴∠DEO+∠CEF=∠EFC+∠CEF=90°，∴∠DEF=90°∴菱形DEFG是正方形．（3）①当点D落在直线m上；即点D与点N重合，可得6﹣t=2∴t=4．当点E落在直线m上；即点E与点M重合，可得2t=5∴t=2.5．当点F落在直线m上；如图3，由△DOE≌△FCE可得CF=OE=6﹣2t把F （ t，6﹣2t ）代入y=2x+26﹣2t=2t+2∴t=1．当点G落在直线m上；如图4，过G作GH⊥x轴于点H容易证明△DOE≌△GHD；∴GH=OD=6﹣t，HD=OE=2t﹣6∴OH=HD+OD=t把G （6﹣t，t ）代入y=2x+2t=2（6﹣t）+2∴t=．∴当t取4，2.5，1，时，四边形DEFG有一个顶点落在直线m上②如图5中，设DD′交直线m于F，作FG⊥OA于G．由题意，D关于直线m的对称点为点D′，当点D′恰好落在直线l上，∴FG=，AD=t，由△DFG∽△FNG∽△MNO，∴===，∴DG=t，GN=t，∵GN=AN﹣AD﹣DG，∴t=4﹣t﹣t，∴t=．∴t=时，D关于直线m的对称点为点D′，当点D′恰好落在直线l上．。