理论力学第6章A

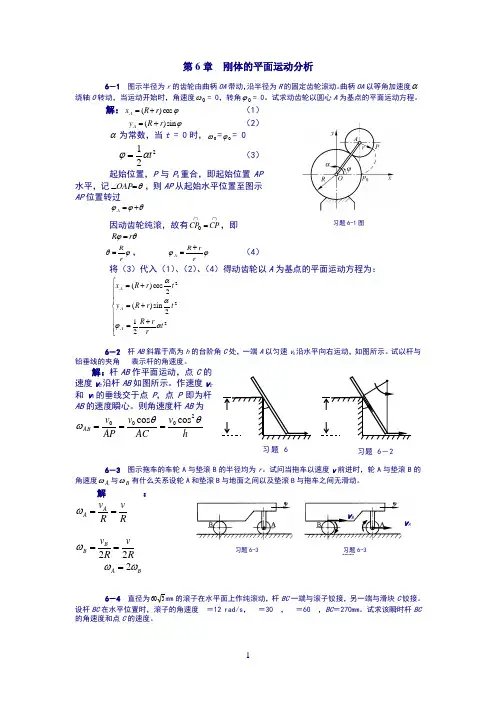
第6章 刚体的平面运动分析6－1 图示半径为r 的齿轮由曲柄OA 带动，沿半径为R 的固定齿轮滚动。

曲柄OA 以等角加速度α绕轴O 转动，当运动开始时，角速度0ω= 0，转角0ϕ= 0。

试求动齿轮以圆心A 为基点的平面运动方程。

解：ϕcos )(r R x A += （1） ϕsin )(r R y A += （2） α为常数，当t = 0时，0ω=0ϕ= 0 221t αϕ=（3）起始位置，P 与P 0重合，即起始位置AP 水平，记θ=∠OAP ，则AP 从起始水平位置至图示AP 位置转过θϕϕ+=A因动齿轮纯滚，故有⋂⋂=CP CP 0，即 θϕr R =ϕθr R =， ϕϕrr R A += （4）将（3）代入（1）、（2）、（4）得动齿轮以A 为基点的平面运动方程为：⎪⎪⎪⎩⎪⎪⎪⎨⎧+=+=+=222212sin )(2cos )(t r r R t r R y t r R x A A A αϕαα6－2 杆AB 斜靠于高为h 的台阶角C 处，一端A 以匀速v 0沿水平向右运动，如图所示。

试以杆与铅垂线的夹角 表示杆的角速度。

解：杆AB 作平面运动，点C 的速度v C 沿杆AB 如图所示。

作速度v C 和v 0的垂线交于点P ，点P 即为杆AB 的速度瞬心。

则角速度杆AB 为hv AC v AP v ABθθω2000cos cos ===6－3 图示拖车的车轮A 与垫滚B 的半径均为r 。

试问当拖车以速度v 前进时，轮A 与垫滚B 的角速度A ω与B ω有什么关系设轮A 和垫滚B 与地面之间以及垫滚B 与拖车之间无滑动。

解：R v R v A A ==ωR v R v B B 22==ω B A ωω2=6－4 直径为360mm 的滚子在水平面上作纯滚动，杆BC 一端与滚子铰接，另一端与滑块C 铰接。

设杆BC 在水平位置时，滚子的角速度＝12 rad/s ，＝30，＝60，BC ＝270mm 。

理论力学a实验报告理论力学实验报告实验目的：1. 通过实验验证牛顿第二定律F=ma，了解质点运动的基本规律。

2. 了解不同质量和不同力作用下质点的加速度变化规律。

3. 学会使用实验数据进行数据处理和结果分析。

实验器材和仪器：1. 弹簧片、纸尺、质量块、电子天平、细线、定滑轮、螺旋测微器等。

实验原理：1. 牛顿第二定律：当质点受到的合外力F（施加力）作用时，它在单位时间内改变的动量等于力乘以时间，即F=ma。

2. 质点的运动方程：当质点受到外力F（恒力）并且无法运动阻力（忽略空气阻力）时，其运动方程为F=ma。

实验内容：1. 利用弹簧片制作一个简单的弹簧振子，测量弹簧振子的恢复力和质量。

2. 在水平桌面上，用细线连接一个质量块和一个拉动质量块的滑轮，用螺旋测微器测量质量块的加速度和受力。

1. 制作弹簧片振子：将弹簧片固定在木板上，细线穿过弹簧片中央孔，并系上质量块于另一端。

2. 用电子天平测量弹簧片和质量块的质量，并测量弹簧片振子的原始长度。

3. 将质量块从平衡位置拉开一小段距离后释放，测量弹簧片振子的振动时间，重复多次并取平均值。

4. 根据实验数据计算弹簧片振子的恢复力和质量，并进行数据处理和分析。

5. 利用细线连接质量块和拉动质量块的滑轮，将螺旋测微器固定在质量块上，并用纸尺测量螺旋测微器的刻度值。

6. 在拉力滑轮上施加一恒力，使质量块受到恒力作用。

同时，利用螺旋测微器测量质量块的加速度，并记录数据多次。

7. 根据实验数据计算质量块的加速度和受力，并进行数据处理和分析。

实验结果与分析：1. 弹簧片振子的恢复力与振子长度成正比，即F=kx，其中k 表示弹性系数，x 表示弹簧片振子的位移。

2. 通过实验数据计算出弹性系数和质量块的质量，并进行误差分析。

3. 质量块的加速度与施加力成正比，即a=F/m，其中F 表示受力，m 表示质量。

4. 通过实验数据计算出质量块的加速度，并进行误差分析。

5. 实验结果与理论分析一致，验证了牛顿第二定律F=ma。

《理论力学A 》考试试题A 课程号：63125203 考试方式： 闭卷 使用专业、年级： 任课教师：考试时间：一、是非题（对画√，错画×）（共5题，每题2分，共10分）1.受平面任意力系作用的刚体，力系的合力为零，刚体就一定平衡。

( )2.定轴转动刚体上各点的角速度相同。

( )3.力系的主矢和主矩都与简化中心的位置有关。

（ ）4.一个刚体若动量为零，该刚体就一定处于静止状态。

（ ）5.定轴转动刚体对其转轴的动量矩等于刚体对其转轴的转动惯量与刚体 角加速度的乘积。

（ ） 二、选择题（共10题，每题3分，共30分）1.图示，已知1F 、2F 、α，则1F 和2F 在x 轴上的投影为 。

（a ）αcos 11F F x =，02=x F ； （b ）αcos 11F F x -=，02=x F ；（c ）αcos 11F F x =，22F F x =； （d ）αcos 11F F x -=，22F F x -= 2.图示杆件的作用力F 对杆端O 点的力矩()=F M O 。

（a ）Fa ； （b ）Fa -； （c ）Fl ； （d ）Fl -3.正立方体如图示，棱长为a ，在A 点作用一力F ，该力对y 轴之矩 为 。

（a ）()Fa F M y = ；（b ）()0=F M y ；（c ）()Fa F M y -= 4.静滑动摩擦因数s f 等于摩擦角f ϕ的 。

（a ）正弦； （b ）正切； （c ）余弦；（d ）余切。

5.如图所示汇交力系的力多边形表示 。

（a ）力系的合力等于零； （b ）力系的合力是R ； （c ）力系的主矩不为零。

6. 图示均质细直杆，质量为m ，长为l ，绕O 轴转动的角速度为ω，则杆的 动量大小为 。

（a ）ωml 21； （b ）ωml ； （c ）07.均质滑轮半径为R ，对O 轴的转动惯量为J ，绳子的一端绕在滑轮上， 另一端挂有质量为m 的物体A 。

绪论单元测试1.下面哪些运动属于机械运动？A:变形B:平衡C:转动D:发热答案:ABC2.理论力学的内容包括：。

A:运动学B:静力学C:动力学D:基本变形答案:ABC3.理论力学的研究对象是：。

A:力学定理B:数学模型C:力学知识D:力学模型答案:D4.矢量力学方法（牛顿-欧拉力学）的特点是：。

A:以牛顿定律为基础B:以变分原理为基础C:通过力的功（虚功）表达力的作用D:通过力的大小、方向和力矩表达力的作用答案:AD5.学习理论力学应注意做到：。

A:准确地理解基本概念B:学会一些处理力学问题的基本方法C:理论联系实际D:熟悉基本定理与公式，并能在正确条件下灵活应用答案:ABCD第一章测试1.如图所示，带有不平行的两个导槽的矩形平板上作用一力偶M,今在槽内插入两个固连于地面的销钉，若不计摩擦，则。

A:在矩M较小时，板可保持平衡B:板不可能保持平衡状态C:板必保持平衡状态D:条件不够，无法判断板平衡与否答案:B2.A:合力偶B:力螺旋C:合力答案:B3.关于力系与其平衡方程式，下列的表述中正确的是：A:平面力系如果平衡，则该力系在任意选取的投影轴上投影的代数和必为零。

B:平面一般力系的平衡方程式可以是三个力矩方程，也可以是三个投影方程。

C:在求解空间力系的平衡问题时，最多只能列出三个力矩平衡方程式。

D:任何空间力系都具有六个独立的平衡方程式。

E:在平面力系的平衡方程式的基本形式中，两个投影轴必须相互垂直。

答案:A4.A:选项AB:选项CC:选项DD:选项B答案:D5.图示一倾斜角α=20°的斜面上的物块重G=980N。

物块与斜面间的静摩擦因数fs=0.2，动摩擦因数f=0.17。

当水平主动力FP=100N时，问物块是否滑动，这时摩擦力为多大？A:静止，摩擦力的值为162.4N。

B:静止，摩擦力的值为241.2 N。

C:滑动，摩擦力的值为162.4 N。

D:滑动，摩擦力的值为241.2 N。

理论力学第七版课后习题答案第一章: 引言习题1-11.问题描述：给定物体的质量m=2kg，加速度a=3m/s^2，求引力F。

2.解答：根据牛顿第二定律F=ma，其中m表示物体的质量，a表示物体的加速度。

代入已知值，可求得F=6N。

习题1-21.问题描述：给定物体的质量m=5kg，引力F=20N，求加速度a。

2.解答：根据牛顿第二定律F=ma，将已知值代入，可求得a=4m/s^2。

第二章: 运动的描述习题2-11.问题描述：一个物体以恒定速度v=10m/s匀速直线运动，经过t=5s，求物体的位移。

2.解答：位移等于速度乘以时间，即s=vt。

代入已知值，可得s=50m。

习题2-21.问题描述：一个物体以初始速度v0=5m/s匀加速直线运动，加速度a=2m/s^2，经过t=3s，求物体的位移。

2.解答：由于物体是匀加速直线运动，位移可以通过公式s=v0t+0.5at^2计算。

代入已知值，可得s=(53)+(0.52*3^2)=45m。

第三章: 动力学基础习题3-11.问题描述：一个物体质量为m=4kg，受到的力F=10N，求物体的加速度。

2.解答：根据牛顿第二定律F=ma，将已知值代入，可求得a=2.5m/s^2。

习题3-21.问题描述：一个物体质量为m=3kg，受到的力F=6N，求物体的加速度。

2.解答：根据牛顿第二定律F=ma，将已知值代入，可求得a=2m/s^2。

第四章: 动力学基本定理习题4-11.问题描述：一个物体质量为m=8kg，受到的力F=16N，求物体的加速度。

2.解答：根据牛顿第二定律F=ma，将已知值代入，可求得a=2m/s^2。

习题4-21.问题描述：一个物体质量为m=6kg，受到的力F=12N，求物体的加速度。

2.解答：根据牛顿第二定律F=ma，将已知值代入，可求得a=2m/s^2。

以上是理论力学第七版课后习题的答案。

希望能对你的学习有所帮助！。

1第一 静力学公理和物体的受力分析一、是非判断题1.1.1 在任何情况下，体内任意两点距离保持不变的物体称为刚体。

( ∨ ) 1.1.2 物体在两个力作用下平衡的必要与充分条件是这两个力大小相等、方向相反，沿同一直线。

( × ) 1.1.3 加减平衡力系公理不但适用于刚体，而且也适用于变形体。

( × ) 1.1.4 力的可传性只适用于刚体，不适用于变形体。

( ∨ ) 1.1.5 两点受力的构件都是二力杆。

( × ) 1.1.6 只要作用于刚体上的三个力汇交于一点，该刚体一定平衡。

( × ) 1.1.7 力的平行四边形法则只适用于刚体。

( × ) 1.1.8 凡矢量都可以应用平行四边形法则合成。

( ∨ ) 1.1.9 只要物体平衡，都能应用加减平衡力系公理。

( × ) 1.1.10 凡是平衡力系，它的作用效果都等于零。

( × ) 1.1.11 合力总是比分力大。

( × ) 1.1.12 只要两个力大小相等，方向相同，则它们对物体的作用效果相同。

( × ) 1.1.13 若物体相对于地面保持静止或匀速直线运动状态，则物体处于平衡。

( ∨ ) 1.1.14 当软绳受两个等值反向的压力时，可以平衡。

( × ) 1.1.15 静力学公理中，二力平衡公理和加减平衡力系公理适用于刚体。

( ∨ ) 1.1.16 静力学公理中，作用力与反作用力公理和力的平行四边形公理适用于任何物体。

( ∨ )1.1.17 凡是两端用铰链连接的直杆都是二力杆。

( × ) 1.1.18 如图1.1所示三铰拱，受力F ，F 1作用，其中F 作用于铰C 的销子上，则AC 、BC 构件都不是二力构件。

( × )二、填空题1.2.1 力对物体的作用效应一般分为 外 效应和 内 效应。

1.2.2 对非自由体的运动所预加的限制条件称为 约束 ；约束力的方向总是与约束所能阻止的物体的运动趋势的方向 相反 ；约束力由 主动 力引起，且随 主动 力的改变而改变。

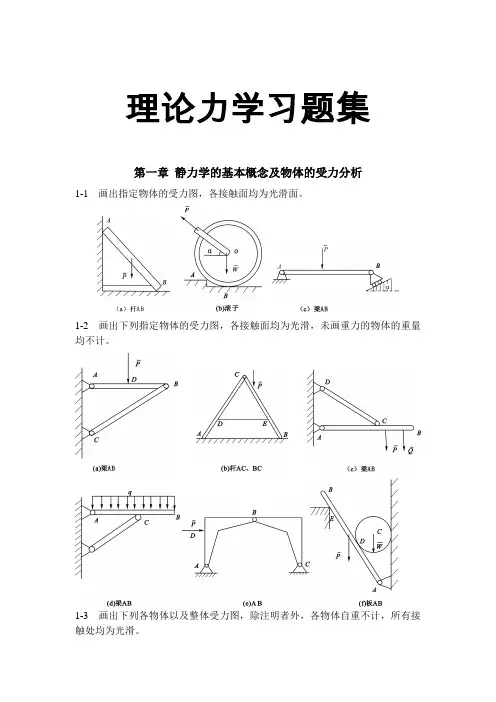
理论力学习题集第一章静力学的基本概念及物体的受力分析1-1 画出指定物体的受力图，各接触面均为光滑面。

1-2 画出下列指定物体的受力图，各接触面均为光滑，未画重力的物体的重量均不计。

1-3 画出下列各物体以及整体受力图，除注明者外，各物体自重不计，所有接触处均为光滑。

(a) (b)(c) (d)(e) (f)第二章平面一般力系2-1 物体重P=20kN，用绳子挂在支架的滑轮B上，绳子的另一端接在铰车D 上，如图所示。

转动铰车，物体便能升起，设滑轮的大小及滑轮转轴处的摩擦忽略不计，A、B、C三处均为铰链连接。

当物体处于平衡状态时，试求拉杆AB和支杆CB所受的力。

2-2 用一组绳悬挂重P=1kN的物体，求各绳的拉力。

2-3 某桥墩顶部受到两边桥梁传来的铅直力P1=1940kN，P2=800kN及制动力T=193kN，桥墩自重W=5280kN，风力Q=140kN。

各力作用线位置如图所示，求将这些力向基底截面中心O简化的结果，如能简化为一合力，试求出合力作用线的位置。

2-4 水平梁的支承和载荷如图所示，试求出图中A、B处的约束反力。

2-5 在图示结构计算简图中，已知q=15kN/m，求A、B、C处的约束力。

2-6 图示平面结构，自重不计，由AB、BD、DFE三杆铰接组成，已知：P=50kN，M=40kN·m，q=20kN/m，L=2m，试求固定端A的反力。

图2-6 图2-72-7 求图示多跨静定梁的支座反力。

2-8 图示结构中各杆自重不计，D、E处为铰链，B、C为链杆约束，A为固定端，已知：q G=1kN/m，q=1kN/m，M=2kN·m，L1=3m，L2=2m，试求A、B、C 处约束反力。

图2-8 图2-92-9 支架由两杆AO、CE和滑轮等组成，O、B处为铰链，A、E是固定铰支座，尺寸如图，已知：r=20cm，在滑轮上吊有重Q=1000N的物体，杆及轮重均不计，试求支座A和E以及AO杆上的O处约束反力。

《理论力学》——期末考试答案一、单选题1.力对点之矩决定于( )。

A.力的大小B.力臂的长短C.力的大小和力臂的长短D.无法确定正确答案：C2.动点相对于动坐标系的运动称为( )的运动。

A.牵连运动B.相对运动C.绝对运动D.圆周运动正确答案：B3.动点的牵连速度是指该瞬时牵连点的速度，它相对的坐标系是( )。

A.动坐标系B.不必确定的C.静坐标系D.静系或动系都可以正确答案：C4.在质点系动能定理中，应注意外力或内力做的功之和不等于合外力或( )做的功。

A.重力B.浮力C.合内力D.牵引力正确答案：C5.将平面力系向平面内任意两点进行简化，所得主矢量和主矩都相等，且主矩不为零，则该力系简化的最后结果为( )。

A.合力偶B.合力C.平衡力系D.无法进一步合成正确答案：A6.超静定结构的超静定次数等于结构中( )。

A.约束的数目B.多余约束的数目C.结点数D.杆件数正确答案：B7.静不定系统中，多余约束力达到3个，则该系统静不定次数为( )A.3次B.6次C.1次D.不能确定正确答案：A8.关于平面力偶系、平面汇交力系、平面一般力系，最多能够得到的相互独立的平衡方程的个数依次是( )。

A.2、1、3B.2、2、3C.1、2、2D.1、2、3正确答案：D9.平面任意力系向一点简化，应用的是( )。

A.力的平移定理B.力的平衡方程C.杠杆原理D.投影原理正确答案：A10.对于平面力系，一个平衡方程可解( )未知量。

A.1个B.2个C.3个D.不一定正确答案：A11.一平面力系由两组平面平行力系组成(这两组平面平行力系之间互不平行),若力系向某A点简化结果为一合力，下述说法正确的是( )。

A.这两组平面平行力系必然都各自向A点简化为一合力B.这两组平面平行力系可能都各自简化为一力偶C.可能一组平面平行力系向A点简化得到一个力和一个力偶，而另一组平面平行力系向A点简化得到一合力D.可能这两组平面平行力系都各自向A点简化得到一个力和一个力偶正确答案：D12.在任何情况下，在几何可变体系上增加一个二元体后构成的体系是几何( )体系。

第六章 刚体的基本运动 习题全解[习题6-1] 物体绕定轴转动的运动方程为334t t -=ϕ（ϕ以rad 计，t 以s 计）。

试求物体内与转动轴相距m r 5.0=的一点，在00=t 与s t 11=时的速度和加速度的大小，并问物体在什么时刻改变它的转向？ 解：角速度： 2394)34(t t t dt ddt d -=-==ϕω 角加速度：t t dtddt d 18)94(2-=-==ωα速度： )94(2t r r v -==ω)/(2)094(5.0|20s m r v t =⨯-⨯===ω)/(5.2)194(5.0|21s m v t -=⨯-⨯==切向加速度：rt t r a t 18)18(-=-==ρα法向加速度：22222)94()]94([t r rt r v a n -=-==ρ 加速度： 422222222)94(324])94([)18(t t r t r rt n a a n t -+=-+-=+=)/(8165.0)094(0324|24220s m r a t =⨯=⨯-+⨯== )/(405.1581.305.0)194(1324|24221s m r a t =⨯=⨯-+⨯== 物体改变方向时，速度等于零。

即：0)94(2=-=t r v )(667.0)(32s s t ==[习题6-2] 飞轮边缘上一点Ｍ，以匀速ｖ＝１０ｍ／ｓ运动。

后因刹车，该点以)/(1.02s m t a t =作减速运动。

设轮半径Ｒ＝０.４ｍ，求Ｍ点在减速运动过程中的运动方程及ｔ＝２ｓ时的速度、切向加速度与法向加速度。

解：t dtd a t 1.04.022-===ϕρα （作减速运动，角加速度为负）t dt d 25.022-=ϕ12125.0C t dtd +-=ϕ2130417.0C t C t ++-=ϕ12124.005.0)125.0(4.0C t C t dtd R v +-=+-⨯==ϕ104.0005.0|120=+⨯-==C v t图题46-251=C0000417.0|2130=+⨯+⨯-==C C t ϕ 02=C ，故运动方程为： t t 250417.03+=ϕt t t t R s 100167.0)250417.0(4.033+-=+-==ϕ速度方程：1005.02+-=t v)/(8.910205.0|22s m v t =+⨯-== 切向加速度：)/(2.021.01.0|22s m t a t t -=⨯-=-== 法向加速度：222)25125.0(4.0+-⨯==t a n ρω)/(1.240)252125.0(4.0|2222s m a t n =+⨯-⨯==[习题6-3] 当起动陀螺罗盘时，其转子的角加速度从零开始与时间成正比地增大。

理论力学试题库题型：A 填空题，B 选择题，C 简答题，D 判断题，E 计算题，F 综合题，G 作图题。

编号E04001中，E 表示计算题，04表示内容的章节号即题目内容属于第04章，001表示章节题号的序号，即此题是第04章计算题的001号题。

计算题:06：E06001. （10分）如图E06001所示曲柄滑杆机构中，滑杆上有一圆弧滑道，其半径R=100mm ，圆心O1在导杆BC 上。

曲柄OA 长100mm ，以等角速度ω=4 rad/s 绕O 轴转动。

求导杆BC 的运动规律以及当曲柄与水平线间交角ϕ=30°时导杆BC 的速度和加速度。

图E06001E06002. （10分）如图E06002所示机构中，假定杆AB 以匀速v 运动，开始时ϕ=0，求当4πϕ=时摇杆OC 的角速度和角加速度。

图E06002E06003.（10分）图示曲柄滑杆机构中，滑杆上有一圆弧形滑道，其半径R=100mm，圆心在导杆BC上。

曲柄长OA=100mm，以等角速度绕O轴转动。

求导杆BC 的运动规律以及当曲柄与水平线间的交角为30°时，导杆BC的速度和加速度。

图E06003E06004.（10分）图示为把工件送入干燥炉内的机构，叉杆OA=1.5m，在铅垂面内转动，杆AB=0.8m，B端为铰链，B端有放置工件的框架。

在机构运动时，工件的速度恒为0.05m/s，杆AB始终铅垂。

设运动开始时，角ϕ=0。

求运动过程中角ϕ与时间的关系，以及点B的轨迹方程。

图E06004E06005.（10分）已知搅拌机的主动齿轮以n=950 r/min 的转速转动。

搅杆ABC 用销钉A，B与齿轮O2, O3相连，如图所示。

且AB=O2 O3, O3A=O2B=0.25m，各齿轮齿数为z1=20，z2=50，z3=50。

求搅杆端点C的速度和轨迹。

图E06005E06006. （10分）机构如图所示，假定杆AB 以匀速v 运动，开始时0=ϕ。

理论力学6章作业题解6-5 半圆形凸轮以匀速v =10mm/s 沿水平方向向左运动,活塞杆AB 长l ，沿铅直方向运动。

当运动开始时,活塞杆A 端在凸轮的最高点上。

如凸轮的半径R =80mm ，求活塞B 的运动方程和速度方程。

解答 选铅直方向为y 坐标，圆心与轮心O 高程相同，则活塞B 的运动方程为)( 1006400)(222mm l t AB vt R y +-=+-=速度方程为)/( 641022s mm t t dt dy v --== 6-9 点M 以匀速率u 在直管OA 内运动，直管OA 又按t w j =规律绕O 转动。

当t=0时， M 在O 点，求其在任一瞬时的速度及加速度的大小。

解答 采用直角坐标法建立M 点的运动方程。

îíì====)sin(sin )cos(cos t ut ut y t ut ut x w j w j 速度分量及大小为îíì+==-==)cos()sin(/)sin()cos(/t t u t u dt dy v t t u t u dt dx v yx w w w w w w 222)(1t u v v v y x w +=+=加速度分量及大小为ïîïíì-+==---==)sin()cos()cos(/)cos()sin()cos(/22t t u t u t u dt dv a t t u t u t u dt dv a y yx x w w w w w w w w w w w w 222)(4t u a a a y x w w +=+=6-12 一点作平面曲线运动，其速度方程为3=x v 、)4sin(2t v y p p =，其中速度单位为m/s ，时间单位为s 。

已知初瞬时该点在坐标原点，试求该点的运动方程和轨迹方程。

解 求直角坐标表示的运动方程。

1第六章点的运动学1．点以匀速率沿阿基米德螺线由外向内运动，如图所示，则点的加速度（则点的加速度（）。

① 不能确定不能确定② 越来越小越来越小③ 越来越大越来越大④ 等于零等于零正确答案：③2．动点M 作曲线运动，某瞬时点的速度v = 4m/s ，点的切向加速度，点的切向加速度 τa = - 2m/s 2，一秒钟后点的速度大小用v 1表示，则（表示，则（）。

① v 1 = 4m/s ②v 1 = 2m/s ③ v 1 = 6m/s ④v 1 无法确定无法确定 正确答案：④3．动点M 沿其轨迹运动时，下列几种情况中，正确的应该是（沿其轨迹运动时，下列几种情况中，正确的应该是（）。

① 若始终有v ⊥ a ，则必有v 的大小等于常量的大小等于常量② 若始终有v ⊥ a ，则点M 必作匀速圆周运动必作匀速圆周运动③ 若某瞬时有v // a ，则点M 的轨迹必为直线的轨迹必为直线④ 若某瞬时有a 的大小等于零，且点M 作曲线运动，则此时速度必等于零作曲线运动，则此时速度必等于零 正确答案：①4．点的切向加速度与其速度（．点的切向加速度与其速度（ ）的变化率无关，而点的法向加速度与其速度（）的变化率无关，而点的法向加速度与其速度（ ）的变化率无关。

无关。

① 大小大小 ② 方向方向正确答案： ② ①5．点作曲线运动时，“匀变速运动”指的是（“匀变速运动”指的是（）。

① a τ= 常矢量常矢量 ② a τ= 常量常量③ a = 常矢量常矢量 ④ a = 常量常量正确答案： ②6．绳子的一端绕在滑轮上，另一端与置于水平面上的物块B 相连，若物块B 的运动方程为x = kt 2，其中k 为常数，轮子半径为R ，则轮缘上A 点的加速度的大小为（点的加速度的大小为（）。

① k 2② 21222)/4(R t k③ 212442)/164(R t k k +④ R t k k /4222+正确答案： ③27．点作曲线运动时，法向加速度等于零的情况，可能是（．点作曲线运动时，法向加速度等于零的情况，可能是（）或（）或（ ）。

6－1在图示四连杆机构中，已知：匀角速度O ω，OA =B O 1=r 。

试求在°=45ϕ且AB ⊥B O 1的图示瞬时，连杆AB 的角速度AB ω及B 点的速度。

解：连杆AB 作平面运动，由基点法得BA A B v v v +=由速度合成的矢量关系，知φcos v A BA =v杆AB 的角速度)(/AB /O BA AB 2122+==ωωv （逆时针）B 点的速度2245/r cos v O A B ω=°=v （方向沿AB ）6－2. 在图示四连杆机构中，已知：3.021===L B O OA m ，匀角速度2=ωrad/s 。

在图示瞬时，11==L OB m ，且杆OA 铅直、B O 1水平。

试求该瞬时杆B O 1的角速度和角加速度。

解：一．求1ω60230..OA v A =×=⋅=ω m/s取A 为基点，则有BA A B v v v += 得 23.0/6.0ctg v v A B ===ϕ m/sm09.2)3.01()3.0/6.0(sin /v v 2/122A BA =+×==ϕ杆B O 1的角速度67630211../BO /v B ===ω rad/s 顺时针 二．求1ε取点A 为基点，则有n BA A a a a a a ++=+ττBA nB B将上式向X 轴投影21222857s /m .B O /ctg v )sin AB /v (OA ctg a )sin /a (a a a sin a cos a sin a BBA n B n BA A B nBA A n B B +=⋅+⋅+⋅−=++−=−=+−ϕϕωϕϕϕϕϕττ杆B O 1的角加速度7.1923.0/8.57/11===B O a B τεrad/s 2逆时针6－3.图示机构中，已知：OA =0.1m ， DE =0.1m ，m 31.0=EF ，D 距OB 线为h=0.1m ；rad 4=OA ω。