当前位置：文档之家 › 理论力学第6章习题解答

理论力学第6章习题解答

  • 格式：doc
  • 大小：1.19 MB
  • 文档页数：17

下载文档原格式

  / 17

合集下载

理论力学-点的运动

理论力学-点的运动
第6章 点 的 运 动
作 业: 6-1, 6-2, 6-3, 6-4, 6-5
例题
点
的 运 动
作业6- 1
一人在路灯下由灯柱起以匀速 u 沿直线背离灯柱
行走。设人高AB=l，灯高OL=h，试求头顶影子M 的 速度和加速度。
L A l B O ut M x
h
x
例题
点
的 运 动
作业6- 2
y A O

C
l
B x
例题
点
的 运 动
作业6- 3
解:
考虑滑块 B 在任意位置，由几何关系得滑块 B 的坐标
r x r cos t l 1 sin 2 t . l
2
将φ=ωt 代入上式得 令λ= r/l，将上式的根式展
开，有
x OC CB r cos l 2 r 2 sin 2
将上式对时间积分一次，并设C点为动点A在
D ρ A C R
t=0时的初始位置，于是得以极坐标表示的A点相对 于凸轮的运动方程
φ
t R vt
消去时间 t，得A点在凸轮上的轨迹方程 v R 凸轮转动，杆AB匀速上升，v，ω为常值，上式为 阿基米得螺旋线。
例题
点
的 运 动
作业6- 5
飞机在铅直面内从位置M0 处以s=250t+5t2 规律沿半径 r=1 500 m的圆弧作机动飞行（如图），其中s以m计，t以 s计，当t=5s时，试求飞机在轨迹上的位置M及其速度和 加速度。
O M0
r
M
例题
点
的 运 动
作业6- 5
解：因已知飞机沿圆弧轨迹的运动方程，宜用

理论力学 陈立群 第6章动习题解答

理论力学 陈立群 第6章动习题解答

第六章 刚体的平面运动 习题解答6-1 椭圆规尺AB 由曲柄OC 带动，曲柄以角速度Oω绕O 轴匀速转动，如图所示。

如r AC BC OC ===，并取C 为基点，求椭圆规尺AB 的平面运动方程。

解：AB 杆作平面运动，设0=t 时，0=ϕ，则t 0ωϕ=。

选AB 杆上的C 点位基点，建立平移坐标系y x C ''-，在图示坐标系中，AB 杆在固定坐标系xy O -的位置由坐标),,(ϑC C y x 确定，所以AB 杆的平面运动方程为：t r x C 0cos ω=，t r y C 0sin ω=，t 0ωϕθ==.6-2 杆AB 的A 端沿水平线以等速v 运动，在运动时杆恒与一半圆周相切，半圆周半径为R ，如图所示。

如杆与水平线的夹角为θ，试以角θ表示杆的角速度。

解： 解法一：杆AB 作平面运动。

选取A 为基点，由速度基点法CA A C v v v +=， 作图示几何关系，图中v v A =，解得θθsin sin v v v A CA ==，A B 杆的角速度为 θθωcos sin 2R v AC v CA ==（逆时针）.解法二：在直角三角形△ACO 中， xR =ϑsin 上式对时间求导，得x xR 2cos -=ϑϑ 其中，ϑ,R x v x== ，解得A B 杆的角速度为 Rv ϑϑϑcos sin 2-= ，（负号表示角速度转向与ϑ角增大的方向相反，即逆时针）6-3 半径为r 的齿轮由曲柄OA 带动，沿半径为R 的固定齿轮转动，如图所示。

如曲柄OA 以等角加速度α绕O 轴转动，当运动开始时，角速度0=O ω，转角0=ϕ。

求动齿轮以中心A 为基点的平面运动方程。

解：动齿轮作平面运动。

建立与曲柄OA 固结的转动坐标系题6-1图题 6-2图题6-3图ξη-O ，和在动齿轮的A 点建立平移坐标系y x A ''-，如图所示，从图中可见，因动齿轮和固定齿轮间没有滑动，所以存在关系ϑϕr R =小轮半径AM 相对平移坐标系y x A ''-，也即固定坐标系得转角为)1(r R A +=+=ϕϑϕϕ, 而 221t αϕ=，可得小轮平面运动方程为)21cos()(2t r R x A α+=， )21sin()(2t r R y A α+=.6-4 图示机构中，已知10.OA =m ，10.BD =m ，10.DE =m ，310.EF =m ；4=OA ωrad/s 。

理论力学简明教程第六章答案

理论力学简明教程第六章答案

第六章 分析力学滔滔长江东逝水，浪花淘尽英雄。

达朗贝尔，拉格朗日，哈密顿等许多前贤相聚于此“力学论剑”，其“冲击波”使非线性问题也不攻自破。

长江后浪推前浪，你或许在此能够加倍“忘乎因此‘。

微分方程将叱咤风云。

[要点分析与总结]1虚功原理：（平稳时）理想条件下，力学系的平稳条件是各质 点上的主动力所作的虚功之和为零：10ni i i W F r δδ==•=∑用广义坐标来表述：310n ii i x W F q q ααδδ=∂==∂∑ 2达朗贝尔原理（动力学下的虚功原理）： 1()0ni i i i i W F m r r δδ==-•=∑〈析〉r δ，W δ均是在时刻未转变（0dt =）时所假想的量，而广义坐标a q 能够是角度，长度或其它的独立的坐标变量。

3拉格朗日方程()d T TQ dt q q ααα∂∂-=∂∂ (1,2,3,,)a s =在保守力下，取拉氏数 L T V =-方程为：()0d L L dt q q αα∂∂-=∂∂ 假设拉氏数中L 不显含广义坐标q β，那么：0Lq β∂=∂ 即 循环积分： Lp const q ββ∂==∂ 4微振动非线性系统在小角度近似下，对拉氏方程的应用 5哈密顿函数与正那么方程 （1） 哈密顿函数1(,,)sH p q t L p q ααα==-+∑式中T Lp q q ααα∂∂==∂∂为广义坐标动量 （2） 正那么方程Hq P Hp q H Lt tαααα∂=∂∂=-∂∂∂=-∂∂ (1,2,3,,)a s =假设哈氏函数H 中不显含广义坐标q β，那么：0Hp q ββ∂=-=∂ 即：循环积分 Tp const q ββ∂==∂ 在稳固条件下（H 中不显含t ），12sp q T ααα==∑那么有能量积分：H T V =+6泊松括号1[,]()sG H G HG H q p p q ααααα=∂∂∂∂=-∂∂∂∂∑ 7哈密顿原理与正那么变换 （1）哈密顿原理保守力系下：210t t Ldt δ=⎰概念：21t t S Ldt =⎰为主函数（3） 正那么变换通过某种变数的变换，找到新的函数*H ，使正那么方程的形式不变（相当于坐标变换）。

理论力学习题答案

理论力学习题答案

理论力学习题答案(总26页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--2第一章 静力学公理和物体的受力分析一、是非判断题在任何情况下，体内任意两点距离保持不变的物体称为刚体。

( ∨ ) 物体在两个力作用下平衡的必要与充分条件是这两个力大小相等、方向相反，沿同一直线。

( × ) 加减平衡力系公理不但适用于刚体，而且也适用于变形体。

( × ) 力的可传性只适用于刚体，不适用于变形体。

( ∨ ) 两点受力的构件都是二力杆。

( × ) 只要作用于刚体上的三个力汇交于一点，该刚体一定平衡。

( × ) 力的平行四边形法则只适用于刚体。

( × ) 凡矢量都可以应用平行四边形法则合成。

( ∨ ) 只要物体平衡，都能应用加减平衡力系公理。

( × ) 凡是平衡力系，它的作用效果都等于零。

( × ) 合力总是比分力大。

( × ) 只要两个力大小相等，方向相同，则它们对物体的作用效果相同。

( × )若物体相对于地面保持静止或匀速直线运动状态，则物体处于平衡。

( ∨ )当软绳受两个等值反向的压力时，可以平衡。

( × )静力学公理中，二力平衡公理和加减平衡力系公理适用于刚体。

( ∨ )静力学公理中，作用力与反作用力公理和力的平行四边形公理适用于任何物体。

( ∨ )凡是两端用铰链连接的直杆都是二力杆。

( × )如图所示三铰拱，受力F ，F 1作用，其中F 作用于铰C 的销子上，则AC 、BC 构件都不是二力构件。

( × )图3二、填空题力对物体的作用效应一般分为 外 效应和 内 效应。

对非自由体的运动所预加的限制条件称为 约束 ；约束力的方向总是与约束所能阻止的物体的运动趋势的方向 相反 ；约束力由 主动 力引起，且随 主动 力的改变而改变。

理论力学第6章答案

理论力学第6章答案

环 量 为 Γ ， 则 根 据 多 连 通 域 的 斯 托 克 斯 定 理 有 ： Γ − Γ( 0 , 0 ) =
∫∫ Ω dA = 0 ， 即
z
Γ = Γ( 0, 0) = 2πC
6-8
Q圆r = a1 , r = a2是流线 ∴圆r = a1 , r = a2上的流体速度沿切向方向
即 r = a1时，υθ = υ0，υ r = 0；r = a2时，υθ = 0，υr = 0
Ω=
6-9
π (a − a )
2 2 2 1
Γa2 − Γa1
=
0 − 2πa1υ0 2a υ = 2 1 02 2 2 π (a2 − a1 ) a1 − a2
由单连通域的斯托克斯定理可知： Γ k3 = 0 ， Γ k4 = ΩA = 2π r
2 0
ω
k2 ，k4 所在为多连通域，由多连通域的斯托克斯定理可知： Γ k1 − Γ a = 0 ，所以
Γ k1 = Γ a = 2π a 2ω Γ k4 = ΩA = 2π r02ω
Γ k2 = Γ AB + Γ Bo + Γ oC + ΓCD + Γ DA = Γ AB + Γ Bo + Γ oC + ΓCD + Γ DA + Γ BC − Γ BC = Γ AB + Γ Bo + Γ oC + ΓCD + Γ DA + Γ BC + ΓCB = (Γ AB + Γ BC + ΓCD + Γ DA ) + (Γ Bo + Γ oC + ΓCB ) 1 2 π a 2ω = 0 + π a 2ω = 4 2

理论力学(第6章)

理论力学(第6章)

t 已知：O1A=O2B=18cm，AB=O1O2=2R，R=18cm ， 18 t2 求： va , aa s BM
π
加速度合成定理的矢量形式向 直角坐标轴x、y上投影，得：
π aax a a cos 6.67cm / s 2 6 π n n aay ar ae sin 20cm / s 2 6
绝对：大圆周（半径R）
相对：沿OA的直线运动 牵连：定轴转动（绕o轴）
2.速度分析 v a ve 大小 ? 方向 √
ve va 2Rω cos

vr
OM√?√ Nhomakorabeavr ve tan 2 R ω sin ω t
6.3 牵连运动为平移时点的加速度合成定理
点的加速度合成定理：
解：（1） 动点：取顶杆AB的A点 动系：固连在凸轮上。 绝对运动：沿AB竖直方向 的平移。 相对运动：A点沿凸轮边 缘的圆周运动。 牵连运动：动系凸轮沿水 平面向右平移。
已知:
v0
30
2.速度分析
va ve vr
由几何关系可以得到：

3 vB vA v tan 30 v 3
例6-5 平面机构中直杆O1A、O2B平行且等长，分别 绕O1、O2轴转动，直杆的A、B连接半圆形平板，动 点M沿半圆形平板ABD边缘运动，起点为点B。已知 π t， O1A=O2B=18cm，AB=O1O2=2R，R=18cm ， 18 t2 。 s BM
求：当 t 3s 时， 动点M的绝对速度 和绝对加速度。

方向竖直向上
例6-2 刨床的急回机构如图所示。曲柄OA的一端 A与滑块用铰链连接。当曲柄OA以匀角速度ω绕固 定轴O转动时，滑块在摇杆O1B上滑动，并带动杆 O1B绕定轴O1摆动。设曲柄长为OA=r，两轴间距 离OO1=l。 B 求： O ① 曲柄在水平位 A 置时摇杆的角 速度 1 。 ② 滑块A对于摇 杆 的相对角 O1 速度

理论力学答案第六章

《理论力学》第六章作业参考答案习题6-4解：根据题意，A 点的运动可以看作是轴线上与原点O 距离随时间变化的点绕O 点的定轴转动。

由于A 点随摇杆OC 一起转动，由几何关系l vtOD AD==ϕtan得摇杆OC 的运动方程：⎪⎭⎫⎝⎛=l vt arctan ϕ所以摇杆OC 的角速度和角加速度分别为：ϕϕω2cos l v==ϕϕϕα2sin cos 222l v -== 因此当4πϕ=时l v2=ω222l v -=α 答：当4πϕ=时，摇杆OC 的角速度和角加速度分别为2vl 和222v l -。

习题6-6解：（1）轴I 以匀速转动，其轮盘边缘上任意一点的速度为：r nv 301π=两轮盘接触处的速度应相等，即r nv d v 30122πω===所以，轴II 的角速度和角加速度可表示为：d rn302πω=()22225000530d d r n dt d ππωα=-⎪⎭⎫ ⎝⎛-== （2）r d =时，轴II 的角速度和角加速度分别等于：ππω20302==n (rad/s) ππα2500022==r(rad/s 2) 轮B 边缘上一点的切向加速度和法向加速度为πα3.02==R a t(m/s 2) πω6022==R a n (m/s 2)所以，其全加速度为：59222≈+=n t a a a (m/s 2)答：轴II 的角加速度为225000dπα=；当r d =时，轮B 边缘上一点的全加速度为592m/s 2。

习题6-9 解：由于12AB O O =，12O A O B =，则21//O O AB ，杆AC 与齿轮1一起作平动，所以齿轮1上任意一点的速度和加速度均等于A 点的速度和加速度，而两齿轮在接触点的速度和加速度也相等，所以齿轮2边缘上一点的速度和切向加速度分别为t bl l dtd v ωωϕcos == t bl dtdv a t ωωsin 2-== 故当s t ωπ2=时，轮2的角速度和角加速度为 02cos 222===πωωl r b r v 2222222sin ωπωl r b l r b r a a t -=-==答：s t ωπ2=时，轮2的角速度和角加速度分别为0和22b l r ω-。

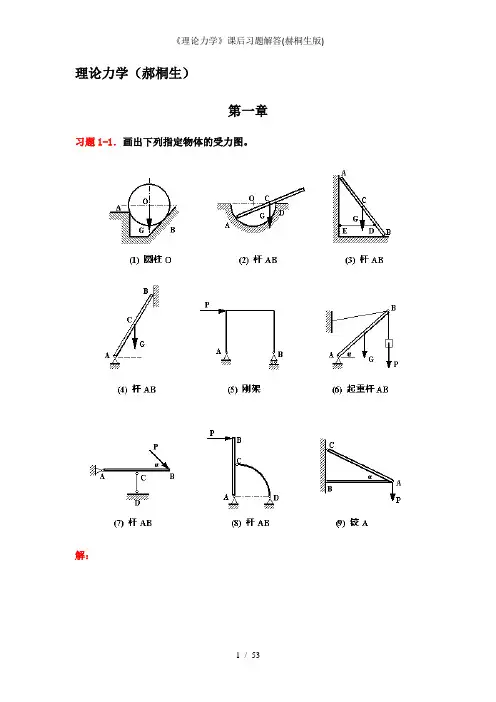
《理论力学》课后习题解答(赫桐生版)

理论力学（郝桐生）第一章习题1-1．画出下列指定物体的受力图。

解：习题1-2．画出下列各物系中指定物体的受力图。

解：习题1-3．画出下列各物系中指定物体的受力图。

解：第二章习题2-1．铆接薄钢板在孔心A、B和C处受三力作用如图，已知P1=100N沿铅垂方向，P2=50N沿AB方向，P3=50N沿水平方向；求该力系的合成结果。

解：属平面汇交力系；合力大小和方向：习题2-2．图示简支梁受集中荷载P=20kN，求图示两种情况下支座A、B的约束反力。

解：(1)研究AB，受力分析：画力三角形：相似关系：几何关系：约束反力：(2) 研究AB，受力分析：画力三角形：相似关系：几何关系：约束反力：习题2-3．电机重P=5kN放在水平梁AB的中央，梁的A端以铰链固定，B端以撑杆BC支持。

求撑杆BC所受的力。

解：(1)研究整体，受力分析：(2) 画力三角形：(3) 求BC受力习题2-4．简易起重机用钢丝绳吊起重量G=2kN的重物，不计杆件自重、磨擦及滑轮大小，A、B、C三处简化为铰链连接；求杆AB和AC所受的力。

解：(1) 研究铰A，受力分析（AC、AB是二力杆，不计滑轮大小）：建立直角坐标Axy，列平衡方程：解平衡方程：AB杆受拉，BC杆受压。

(2) 研究铰A，受力分析（AC、AB是二力杆，不计滑轮大小）：建立直角坐标Axy，列平衡方程：解平衡方程：AB杆实际受力方向与假设相反，为受压；BC杆受压。

习题2-5．三铰门式刚架受集中荷载P作用，不计架重；求图示两种情况下支座A、B的约束反力。

解：(1) 研究整体，受力分析（AC是二力杆）；画力三角形：求约束反力：(2) 研究整体，受力分析（BC是二力杆）；画力三角形：几何关系：求约束反力：习题2-6．四根绳索AC、CB、CE、ED连接如图，其中B、D两端固定在支架上，A端系在重物上，人在E点向下施力P，若P=400N，α=4o，求所能吊起的重量G。

解：(1) 研究铰E，受力分析，画力三角形：由图知：(2) 研究铰C，受力分析，画力三角形：由图知：习题2-7．夹具中所用的两种连杆增力机构如图所示，书籍推力P作用于A点，夹紧平衡时杆AB与水平线的夹角为；求对于工件的夹紧力Q和当α=10o时的增力倍数Q/P。

理论力学(建筑力学第一分册)(邹昭文)课后习题答案


F F ( 56 . 9 56 . 6 0 44 . 7 ) kN 68 . 8 kN Ry y
2-2
y
x F F ( 19 56 . 6 50 89 . 4 ) kN 1 . 8 kN Rx x
F F ( 56 . 9 56 . 6 0 44 . 7 ) kN 68 . 8 kN Ry y
2-5
解：选取刚架为研究对 象，受力图为： 刚架在力F作用下处于平 衡，所以力多边形是自 FA 封闭的，如图。 则，
F F ; F F tan A D cos
y
x
α F
FD FA
FD
AD 2 a 2 CD a cos ; tan 在RT△CAD中， 2 2 AC AD 2 a 5 2 a a F 5 F F F ; F F tan 所以， A cos 2 D 2
以压块C为研究对象，受力如图：
建立坐标系，列平衡方程：
F 0 , F ' cos F 0 x BC D

FD
F’B
C
o 解之得： F F ' cos F cos 8 1 . 08 kN 0 . 99 1 . 07 kN D BC BC

第3章 平面一般力系
3-1（a）
所以合力FR的大小为：
F F F 1 . 8 kN 68 . 8 kN 68 . 82 kN R x y
2 2 2 2
其方向角则为：
F 1 . 8 o Rx arccos arccos 91 . 5 F 68 . 82 R F 68 . 8 Ry o arccos arccos 1 . 38 F 68 . 82 R

理论力学第六章 平衡方程及其应用


第六章 平衡方程及其应用 >> 力偶系的平衡
§6-2 力偶系的平衡 一、平面力偶系的平衡方程 平面力偶系平衡的必要和充分条件是：所有各力偶矩的代数和 等于零，即 M i 0 . 二、空间力偶系的平衡方程
由于空间力偶系可以用一个合力偶来代替，因此，空间力偶系
平衡的必要和充分条件是：该力偶系的合力偶矩等于零，亦即
要使这个刚体平衡，需加一力偶，其力偶矩矢为 -M。
第六章 平衡方程及其应用
§6-3 一般力系的平衡 一、平面一般力系的平衡方程 1. 平面一般力系平衡方程的基本形式
0 MO 0 FR

F
x
0
F
y
0
M
O
(F ) 0
2. 平面一般力系平衡方程的其他形式
（1）二矩式平衡方程
M
FA FB
第六章 平衡方程及其应用 >> 力偶系的平衡 例题6-4 图示（a）所示的三角柱刚体是正方体的一半。在其中三个侧面 各自作用一个力偶。已知力偶（ F1，F1 ）的矩 M 1 20N m ；力偶 （ F2，F2 ）的矩 M 2 20N m ；力偶（ F ，F ）的矩 M 3 20N m 。试 3 3 求合力偶矩矢M。又问使这个刚体平衡，还需要施加怎样一个力偶。
解：根据空间力偶系合成法，先求出力偶
矩矢M。根据三个力偶在空间的作用面不 同，考虑到力偶矩矢是自由矢量，可将力
偶矩矢画在坐标轴上（图 b）。和力偶矩
矢M在三个坐标轴上的投影为
第六章 平衡方程及其应用 >> 力偶系的平衡
M x M 1x M 2 x M 3 x 0
M y M1y M 2 y M 3 y (10 30cos45)N m 11.2 N m
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

6－1在图示四连杆机构中，已知：匀角速度O ω，OA =B O 1=r 。

试求在︒=45ϕ且AB ⊥B O 1的图示瞬时，连杆AB 的角速度AB ω及B 点的速度。

解：连杆AB 作平面运动，由基点法得BA A B v v v +=由速度合成的矢量关系，知φcos v A BA =v杆AB 的角速度)(/AB /O BA AB 2122+==ωωv （逆时针）B 点的速度2245/r cos v O A B ω=︒=v （方向沿AB ）6－2. 在图示四连杆机构中，已知：3.021===L B O OA m ，匀角速度2=ωrad/s 。

在图示瞬时，11==L OB m ，且杆OA 铅直、B O 1水平。

试求该瞬时杆B O 1的角速度和角加速度。

解：一．求1ω60230..OA v A =⨯=⋅=ω m/s取A 为基点，则有BA A B v v v += 得 23.0/6.0ctg v v A B ===ϕ m/sm09.2)3.01()3.0/6.0(sin /v v 2/122A BA =+⨯==ϕ杆B O 1的角速度67630211../BO /v B ===ω rad/s 顺时针二．求1ε取点A 为基点，则有nBA A a a a a a ++=+ττBA nB B 将上式向X 轴投影21222857s /m .BO /ctg v )sin AB /v (OA ctg a )sin /a (a a a sin a cos a sin a BBA n B n BA A B nBA A n B B +=⋅+⋅+⋅-=++-=-=+-ϕϕωϕϕϕϕϕττ杆B O 1的角加速度 7.1923.0/8.57/11===B O a B τεrad/s 2 逆时针 @6－3.图示机构中，已知：OA =0.1m ， DE =0.1m ，m 31.0=EF ，D 距OB 线为h=0.1m ；s rad 4=OA ω。

在图示位置时，曲柄OA 与水平线OB 垂直；且B 、D 和F 在同一铅直线上。

又DE 垂直于EF 。

求杆EF 的角速度和点F 的速度。

6－4.在瓦特行星传动机构中，平衡杆O 1A 绕O 1轴转动，并借连杆AB 带动曲柄OB ；而曲柄OB 活动地装置在O 轴上，如图所示。

在O 轴上装有齿轮I ，齿轮II 与连杆AB 固连于一体。

已知：m 33.021==r r ，O 1A =0.75m ，AB =1.5m ；又平衡杆的角速度rad 61=O ω。

求当︒=60γ且︒=90β时，曲柄OB 和齿轮I 的角速度。

6－5. 使砂轮高速转动的装置如图所示。

杆O 1O 2绕O 1轴转动，转速为n 4。

O 2处用铰链连接一半径为r 2的活动齿轮II ，杆O 1O 2转动时，轮II 在半径为r 3的固定内齿轮III 上滚动，并使半径为r 1的轮I 绕O 1轴转动。

轮I 上装有砂轮，随同轮I 高速转动。

已知1113=r r ，m in r 9004=n 。

求砂轮的转速。

6－6. 图示小型精压机的传动机构，OA=O 1B=r =0.1m ， EB=BD=AD=l =0.4m 。

在图示瞬时，AD OA ⊥，ED B O ⊥1，O 1D 在水平位置，OD 和EF 在铅直位置。

已知曲柄OA 的转速m in r 120=n ，求此时压头F 的速度。

6－7.半径为R的轮子沿水平面滚动而不滑动，如图所示。

在轮上有圆柱部分，其半径为r。

将线绕于圆柱上，线的B端以速度v和加速度a沿水平方向运动。

求轮的轴心O的速度和加速度。

6－8．在图示平面机构中，已知：BC=5cm，AB=10cm，A点以匀速度u A=10m/s 沿水平运动，方向向右；在图示瞬时， =30°，BC杆处于铅垂位置。

试求该瞬时：（1）B点的加速度；（2）AB杆的角加速度；（3）AB杆中点D的加速度。

解：（1）求a B 和εAB()方向如图示为基点则选求逆时针由图中几何关系得则为基点选杆作瞬时平动不垂直于且常量 cm/s 3/3203/45)2(/3/4 10/3/40/cm/s 3/340)2/3/(25 30cos /cos / ,A rad/s25/10/,0,,||0,22AB 222=⨯=⋅==∴++=====⨯=⋅===++=+====∴=∴=AB DA D DAnDA A D DBA BC nB BA B BA n BA A B nB B BC AB A B A A A DA a a a a a a A a s rad AB a BC a a a a a a a a BC V AB V AB V V a V εεωθωωττττττ6－9．平面机构中在图示θ=30°位置时，杆AB 及O 2C 分别处于水平及铅垂位置，O 1A 为铅垂线，O 1A=O 2C=L=10cm ，u A =8cm/s ，αA =0。

试求此瞬时：（1）连杆BC 的角速度ωBC ；（2）杆O 2C 的角速度ω2；（3）杆O 1B 的角加速度。

解：由速度投影定理 AB B AB A V V ][][=/ 0)/60sin (2 60sin 60cos ),0(cm/s 34.6cm/s 8.1220/16/a rad/s8.010/8/, rad/s 6.110/16/ rad/s 8.020/16/ cm/s16 ,C cm/s 1660cos /860cos / 11122222212B 1122BC ==∴=⋅-⋅==++=+==⋅=============∴===+====B O a B O V AB a a a a a a a a a A BA a B O V A O V O AB CO V BC V V V V V V V V V B B AB B n BAn B B nBA BA n B B A AB nBA B nA ABC BC B BC C BC C B A B τττττεωωωωω 得将上式向水平轴投影则有为基点取点有故杆的速度瞬心为点顺时针顺时针故则得为基点取点得6－10. 半径为R 的圆盘沿水平地面作纯滚动，细杆AB 长为L ，杆端B 可沿铅垂墙滑动。

在图示瞬时，已知圆盘的角速度ω0，角加速度为ε0，杆与水平面的夹角为θ。

试求该瞬时杆端B 的速度和加速度。

解：（1）求B VC 1为圆盘速度瞬心，故V A =R ω0 ∵C 2为杆AB 速度速度瞬心，故铅直向下方向方向有上式投影在则为基点选求铅直向下:)sin /( sin /)cos ( cos sin , ,)2( sin /cos sin //3202020000202θωθεθωθεθθεθωθωθωθωωτL R ctg R L R a a a a BA a a a a A R a a ctg R L R L BC V L R AC V AB B nBAA B BAnBA A B A BAB B A AB +=+=∴+=++===⋅=⋅=∴==6－11.如图所示，轮O 在水平面上滚动而不滑动，轮心以匀速s m 2.0=O υ运动。

轮缘上固连销钉B ，此销钉在摇杆O 1A 的槽内滑动，并带动摇杆绕O 1轴转动。

已知：轮的半径R =0.5m ，在图示位置时，AO 1是轮的切线，摇杆与水平面间的交角为︒60。

求摇杆在该瞬时的角速度和角加速度。

6－12.已知图示机构中滑块A 的速度为常值，s m 2.0=A υ，AB =0.4m 。

图示位置AB=BC ，︒=30θ。

求该瞬时杆CD 的速度和加速度。

6－13.平面机构的曲柄OA 长为2a ，以角速度ω0绕轴O 转动。

在图示位置时，AB ＝BO 且 ∠OAD = 90︒。

求此时套筒D 相对于杆BC 的速度。

解：1．分析滑块B02ωa v A =，0e ωa v B =3230cos 0e a ωa v v B B =︒=2．杆AD 作平面运动︒=30cos a D A v v ，340a ωa v D =3．分析滑块D320a e ωa v v B D ==，320e a r ωa v v v D D D =-=6－14.曲柄导杆机构的曲柄OA 长120mm ，在图示位置∠AOB=90︒时，曲柄的角速度ω =4rad/s ，角加速度α = 2 rad/s2。

试求此时导杆AC 的角加速度及导杆相对于套筒B 的加速度。

设OB=160mm 。

v B解：1．v ：分析滑块B （动系）ω⋅=OA v A r a cos cos v OA v v v A B =⋅===θωθθωθsin sin ⋅==OA v v A BAθωθωω22sin sin =⋅==OAOA AB v BA AC2．a ：分析滑块B （动系）α⋅=OA a A t ，2n ω⋅=OA a ArC t n n t a a a aaa a a a +=+++==BABAA A B将上式沿AC 方向投影)43160120(tan ==θ222nn t r mm/s28.545sin sin cos sin cos -=+⋅-⋅=+-=θωθωθαθθOA OA OA a a a a ACBAA A 将加速度的矢量方程沿垂直AC 的方向投影：C AA BA a a a a-=--θθcos sin n t tn t t .574cos sin =-+=C AA BAa a a aθθ，2t rad/s 87.2==ABaBAAC α6－15曲柄连杆机构带动摇杆O 1C 绕O 1轴摆动。

在连杆AB 上装有两个滑块，滑块B 在水平槽内滑动，而滑块D 则在摇杆O 1C 的槽内滑动。

已知：曲柄长OA =50 mm ，绕O 轴转动的匀角速度ω=10 rad/s 。

在图示位置时，曲柄与水平线间成90˚角；摇杆O 1C 与水平线间成60˚角，∠OAB =60︒。

距离O 1D =70mm 。

求摇杆O 1C 的角速度和角加速度。

解（1）机构中曲柄OA 和摇杆O1C 作定轴转动，连杆ABD 作平面运动，滑块B 作水平直线运动，在此瞬时，v A和v B均沿水平方向，故连杆ABD 作瞬时平移，则6－16 平面机构如图所示。

套筒在轮缘上B 点铰接，并可绕B 转动，DE 杆穿过套筒。

已知：r=h=20cm ，OA=40cm 。

在图示位置时，直径AB 水平，杆DE 铅垂，OA 杆的角速度ω=2rad/s 。

试求该瞬时杆DE 的角速度以及角加速度。

解：轮作平面运动 u A =OA·ω=80cm/s 以A 为基点： CA A C u u u+= u C =u A cos60°=40 cm/s以C 为基点： BC C B u u u+=动点：铰链B ，动系：DE r e B u u u+= 即 BC C u u +=r e u u+ 得 u e =u C∴ ωDE =u e /DB=1 rad/s 逆时针a e t =7.57 m/s 2αDE =18.93 rad/s 2 逆时针。