下载文档原格式
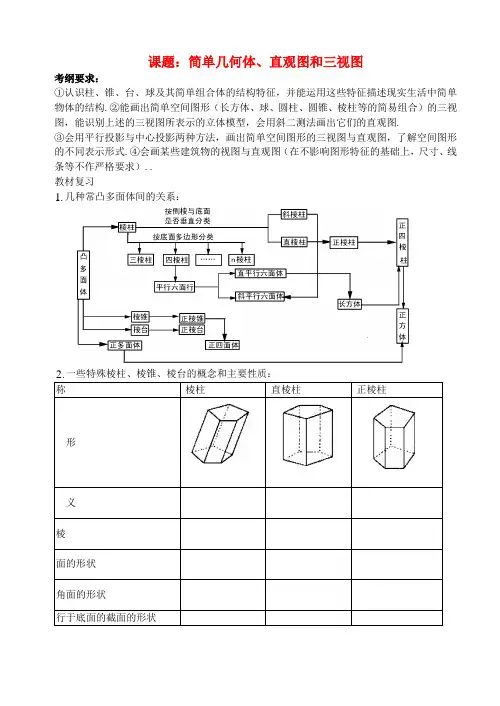
课题：简单几何体、直观图和三视图考纲要求：①认识柱、锥、台、球及其简单组合体的结构特征，并能运用这些特征描述现实生活中简单物体的结构.②能画出简单空间图形（长方体、球、圆柱、圆锥、棱柱等的简易组合）的三视图，能识别上述的三视图所表示的立体模型，会用斜二测法画出它们的直观图.③会用平行投影与中心投影两种方法，画出简单空间图形的三视图与直观图，了解空间图形的不同表示形式.④会画某些建筑物的视图与直观图（在不影响图形特征的基础上，尺寸、线条等不作严格要求）..教材复习1.几种常凸多面体间的关系：几种特殊四棱柱的特殊性质基础知识方法1.三视图画法的关键是要分清观察者的方向，应从前面到后面，左面到右面，上面向下面三个方向去观察图形；画三视图时要做到“长对正，宽相等，高平齐”。
2.斜二测画法要注意其规则：“横不变，纵折半，保平行”.典例分析：考点一空间几何体的结构特征问题1．()1（2012哈师大附中月考）下列结论正确的是.A各个面都是三角形的几何体是三棱锥.B以三角形的一条边所在直线为旋转轴，其余两边旋转形成的曲面所围成的几何体叫圆锥.C棱锥的侧棱长与底面多边形的边长相等，则此棱锥可能是六棱锥.D圆锥的顶点与底面圆周上的任意一点的连线都是母线()2有下列四个命题：①底面是矩形的平行六面体是长方体；②棱长相等的直四棱柱是正方体；③有两条侧棱都垂直于底面一边的平行六面体是直平行六面体；④对角线相等的平行六面体是直平行六面体．其中真命题的个数是.A1.B2.C3.D4()3(06江西文)如果四棱锥的四条侧棱都相等，就称它为“等腰四棱锥”，四条侧棱称为它的腰，以下4个命题中，假命题．．．是.A等腰四棱锥的腰与底面所成的角都相等.B等腰四棱锥的侧面与底面所成的二面角都相等或互补.C等腰四棱锥的底面四边形必存在外接圆.D等腰四棱锥的各顶点必在同一球面上()4（05全国Ⅱ文）下面是关于三棱锥的四个命题：①底面是等边三角形，侧面与底面所成的二面角都相等的三棱锥是正三棱锥．②底面是等边三角形，侧面都是等腰三角形的三棱锥是正三棱锥．③底面是等边三角形，侧面的面积都相等的三棱锥是正三棱锥．④侧棱与底面所成的角相等，且侧面与底面所成的二面角都相等的三棱锥是正三棱锥．其中，真命题的编号是（写出所有真命题的编号）考点二简单几何体的三视图问题2．()1(2011江西文) 将长方体截去一个四棱锥， 得到的几何体如右图所示，则该几何体的左视图为()2（07山东文理）下列几何体各自的三视图中，有且仅有两个视图相同的是.A ①② .B ①③ .C ①④ .D ②④()3已知：图①是截去一个角的长方体，试按图示的方向画出其三视图；图②是某几何体的三视图，试说明该几何体的构成．()4(08山东文)右图是一个几何体的三视图，根①正方体 ②圆锥体 ④正四棱锥据图中数据，可得该几何体的表面积是：.A9π.B10π.C11π.D12π()5(09山东文理)一空间几何体的三视图如图所示,则该几何体的体积为考点三简单几何体的直观图问题3．()1如图所示的直观图，其平面图形的面积为.A3.B6.C.D223()2已知正ABC△的边长为a,那么ABC△的直观图AB C'''△的面积为()3（2012四平模拟）已知正三棱锥V ABC-的正视图、侧视图和俯视图如图所示．①画出该三棱锥的直观图；②求出侧视图的面积．俯视图侧(左)视图正(主)视考点四 与简单几何体有关的计算问题4．圆台的一个底面周长是另一个底面周长的3倍，轴截面的面积等于392 2cm ,母线与轴的夹角是45︒，求这个圆台的高、母线长和两底面半径.问题5．求侧面上斜高（棱锥侧面三角形的高）为多少？走向高考：1.（04全国）下面是关于四棱柱的四个命题：①若有两个侧面垂直于底面，则该四棱柱为直四棱柱②若两个过相对侧棱的截面都垂直于底面，则该四棱柱为直四棱柱③若四个侧面两两全等，则该四棱柱为直四棱柱④若四棱柱的四条对角线两两相等，则该四棱柱为直四棱柱 其中，真命题的编号是 （写出所有正确结论的编号）.2.(06江西文) 如图，已知正三棱柱111ABC A B C -的底面边长为1，高为8，一质点自A 点出发，沿着三棱柱的侧面1CA CB绕行两周．．到达1A 点的最短路线的长为3. （2013四川）一个几何体的三视图如图所示，则该几何体的直观图可以是4. （2012湖南）某几何体的正视图和侧视图均如图1所示，则该几何体的俯视图不可能．．．是5. (03北京文理)如果圆台的母线与底面成60︒角,那么这个圆台的侧面积与轴截面面积的比为 .A π2 .B π23 .C π332 .D π216.（2013陕西）某几何体的三视图如图所示,则其体积为 ..A.B .C .D7.（2011陕西）某几何体的三视图如图所示，则它的体积是.A 283π- .B 83π- .C 82π- .D 23π8.（07全国Ⅱ文）一个正四棱柱的各个顶点在一个直径为2 cm 的球面上.如果正四棱柱的底面边长为1 cm ，那么该棱柱的表面积为 2cm9.(01全国文)若一个圆锥的轴截面是等边三角形，其面积为3，则这个圆锥的全面积是 .A π3 .B π33 .C π6 .D π9。
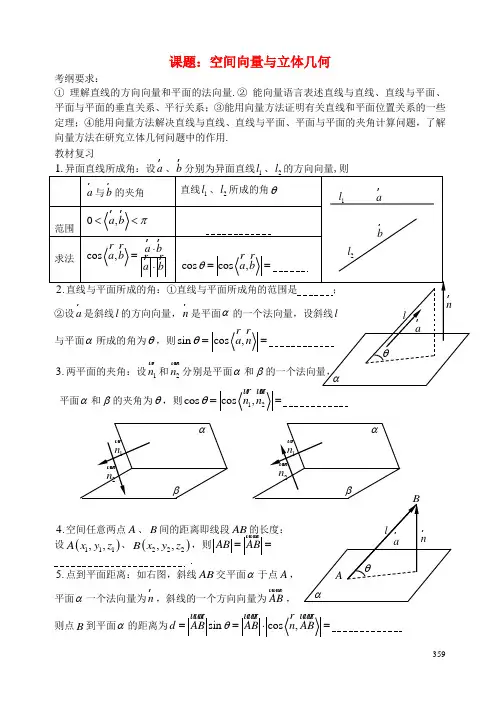
359课题：空间向量与立体几何考纲要求：① 理解直线的方向向量和平面的法向量.② 能向量语言表述直线与直线、直线与平面、平面与平面的垂直关系、平行关系；③能用向量方法证明有关直线和平面位置关系的一些定理；④能用向量方法解决直线与直线、直线与平面、平面与平面的夹角计算问题，了解向量方法在研究立体几何问题中的作用. 教材复习r r平面α和β的夹角为θ，则cos θ=12cos ,n n =4.空间任意两点A 、B 间的距离即线段AB 的长度： 设()111,,A x y z 、()222,,B x y z ，则AB AB ==u u u r.5.点到平面距离：如右图，斜线AB 交平面α于点A ，平面α一个法向量为n r ，斜线的一个方向向量为AB u u u r， 则点B 到平面α的距离为sin cos ,d AB AB n AB θ==⋅=u u u r u u u r r u u u r3606.直线l 的方向向量是a r ，平面α的法向量为n r，则l ∥α⇔ . 7.直线l 的方向向量是a r ，平面α的法向量为n r，则l α⊥⇔ .8.平面α的法向量为1n u r ,平面β的法向量为2n u u r,则αβ⊥⇔ . 9.平面α的法向量为1n u r ,平面β的法向量为2n u u r,则α∥β⇔ .典例分析：考点一 异面直线所成的角问题1． （2012陕西）如图，在空间直角坐标系中有直三棱柱111ABC A B C -，12CA CC CB ==，则直线1BC 与直线1AB 夹角的余弦值为.A 55 .B 53 .C 255 .D 35考点二 直线和平面所成的角问题2．（2013山东）已知三棱柱111ABC A B C -的侧棱与底面垂直，体积为94，底面 是边长为3的正三角形.若P 为底面111A B C 的中心，则PA 与平面ABC 所成角的大小为.A512π .B 3π .C 4π .D 6π考点三 平面和平面的夹角361问题3． （2013陕西）如图, 四棱柱11ABCD A B C D -的底面ABCD 是正方形,O 为底面中心, 1A O ⊥平面ABCD , 1AB AA ==()1证明: 1A C ⊥平面11BB D D ； ()2求平面1OCB 与平面11BB D D 的夹角θ的大小.考点四 求点到平面的距离问题4．（05江西）如图，在长方体1111ABCD A B C D -中，11AD AA ==，2AB =， 点E 在棱AB 上移动.()1略；()2当E 为AB 的中点时，求点E 到面1ACD 的距离；()3略.(请用多种方法，至少要用向量法)D1A1B1C1D1A362考点五 存在性问题问题5：（2013北京）如图，在三棱柱111ABC A B C -中，11AAC C 是边长为4的正方形，平面ABC ⊥平面11AAC C ，3AB =，5BC =.()1求证：1AA 平面ABC （这里不做）；()2求二面角111A BC B --的余弦值（这里不做）；()3证明：在线段1BC 存在点D ，使得1AD A B ⊥，并求1BDBC 的值.1B1A1C BAC363课后作业：1.（2013洛阳联考）在平面直角坐标系中，点A 的坐标为()2,3，点B 的坐标为()1,1--，将直角坐标平面沿x 轴折成直二面角，则,A B 两点间的距离为.A 3 .B .C 5 .D2. （2013辽宁六校联考）如图，平面AED ⊥平面ABCD ，AED △为正三角形，四边形为矩形，F 为CD 的中点，EB 与平面ABCD 所成的角为30︒.()1当AD 长度时，求点A 到平面EFB 的距离；()2二面角A BF E --的大小是否与AD 长度有关?请说明理由.E A BCDF364走向高考：1.（05辽宁）如图，正方体的棱长为1，C 、DA 、B 、M 是顶点，那么点M 到截面ABCD2.如图，正方体1111ABCD A B C D 的棱长为1，O 是底面1111A B C D 的中心，则O 到平面11ABC D 的距离为.A 21.B 42 .C 22 .D 23A BCD1C1D1A1BOg M3653.（2012福建）如图，在长方体1111D C B A ABCD -中，11==AD AA ，E 为CD 中点. （Ⅰ）求证：11AD E B ⊥（这里不做）；（Ⅱ）在棱1AA 上是否存在一点P ，使得//DP 平面AE B 1？若存在，求AP 的长；若不存在，说明理由；（Ⅲ）若二面角11A E B A --的大小为30︒，求AB 的长（这里不做）；。
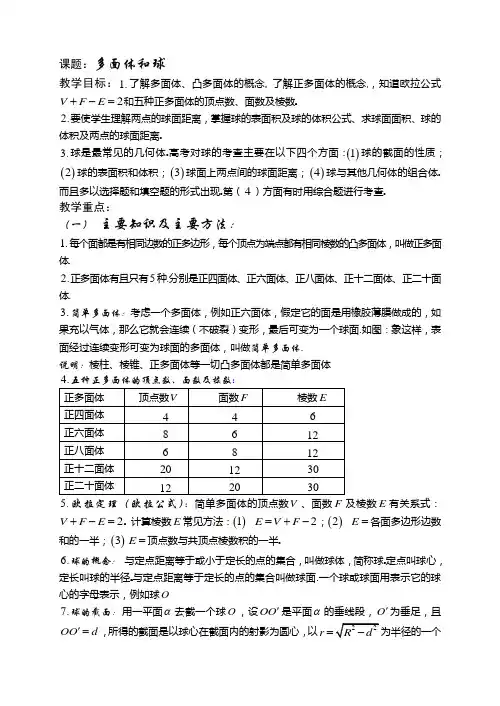
课题：多面体和球教学目标：1.了解多面体、凸多面体的概念 了解正多面体的概念，知道欧拉公式2V F E +-=和五种正多面体的顶点数、面数及棱数2.要使学生理解两点的球面距离，掌握球的表面积及球的体积公式、求球面面积、球的体积及两点的球面距离.3.球是最常见的几何体.高考对球的考查主要在以下四个方面：()1球的截面的性质；()2球的表面积和体积；()3球面上两点间的球面距离；()4球与其他几何体的组合体.而且多以选择题和填空题的形式出现.第（4）方面有时用综合题进行考查. 教学重点：（一） 主要知识及主要方法：1.每个面都是有相同边数的正多边形，每个顶点为端点都有相同棱数的凸多面体，叫做正多面体.2.正多面体有且只有5种.分别是正四面体、正六面体、正八面体、正十二面体、正二十面体.3.简单多面体：考虑一个多面体，例如正六面体，假定它的面是用橡胶薄膜做成的，如果充以气体，那么它就会连续（不破裂）变形，最后可变为一个球面.如图：象这样，表面经过连续变形可变为球面的多面体，叫做简单多面体.说明：棱柱、棱锥、正多面体等一切凸多面体都是简单多面体5.欧拉定理（欧拉公式）：简单多面体的顶点数V 、面数F 及棱数E 有关系式：V F E +-= 计算棱数E 常见方法：()1 2E V F =+-；()2 E =各面多边形边数和的一半；()3E =顶点数与共顶点棱数积的一半.6.球的概念： 与定点距离等于或小于定长的点的集合，叫做球体，简称球定长叫球的半径与定点距离等于定长的点的集合叫做球面.一个球或球面用表示它的球心的字母表示，例如球O7.球的截面：用一平面α去截一个球O ，设OO '是平面α的垂线段，O '为垂足，且OO d '=，所得的截面是以球心在截面内的射影为圆心，以r =为半径的一个圆，截面是一个圆面.球面被经过球心的平面截得的圆叫做大圆，被不经过球心的平面截得的圆叫做小圆 8.两点的球面距离：球面上两点之间的最短距离，就是经过两点的大圆在这两点间的一段劣弧的长度，我们把这个弧长叫做两点的球面距离.l R ϕ=(ϕ为球心角的弧度数).9.球的表面积和体积公式：24S R π=，343V R π=. （二）典例分析：问题1．()1（05辽宁）棱长为a 的正方体，连结相邻面的中心，以这些线段为棱的八面体的体积为 .A 23a .B 24a .C 26a .D 212a()2已知一个正四面体和一个正八面体的棱长相等且为1，把它们拼起来，使一个表面重合，所得的多面体有多少个面？问题2．()1(07天津）一个长方体的各顶点均在同一球的球面上，且一个顶点上的三条棱的长分别为1,2,3，则此球的表面积为()2(07全国Ⅰ文)正四棱锥S ABCD -，点,,,,S A B C D都在同一个球面上，则该球的体积为()3（07江西文）四面体ABCD的外接球球心在CD上，且2CD=，3AB=，在外接球面上两点A、B间的球面距离是.Aπ6.Bπ3.C2π3.D5π6()4（06陕西）水平桌面α上放有4个半径均为2R的球，且相邻的球都相切(球心的连线构成正方形).在这4个球的上面放1个半径为R的小球，它和下面4个球恰好都相切，则小球的球心到水平桌面α的距离是问题3．（07四川）设球O的半径是1，A、B、C是球面上三点，已知A 到B 、C 两点的球面距离都是2π，且二面角B OA C --的大小为3π，则从A 点沿球面经B 、C 两点再回到A 点的最短距离是 .A 67π .B 45π .C 34π .D 23π问题4．三棱锥A BCD -的两条棱6AB CD ==，其余各棱长均为5，求三棱锥的内切球半径和外接球半径.问题5．已知球的半径为R ，在球内作一个内接圆柱，这个圆柱底面半径与高为何值时，它的侧面积最大?侧面积的最大值是多少?（三）课后作业：1.正方体、正多面体、凸多面体、简单多面体是什么关系？2.已知凸多面体每个面都是五边形，每个顶点都有三条棱相交，试求该凸多面体的面数、顶点数和棱数.3.一个广告气球被一束入射角为 的平行光线照射，其投影是一个长半轴为5m的椭圆，则制作这个广告气球至少需要的面料是4.在球面上有四个点P 、A 、B 、C ，如果PA 、PB 、PC 两两互相垂直，且PA PB PC a ===，那么这个球面的面积是 .A 22a π .B 23a π .C 24a π.D 26a π5.北纬30︒的圆把北半球面积分为两部分，这两部分面积的比为.A 1:1 .B 2:1 .C .D6.已知过球面上A 、B 、C 三点的截面和球心的距离等于球半径的一半， 且2AB BC CA ===，则球面面积是.A 9π16 .B 3π8 .C 4π .D 9π647.正八面体的相邻两个面所成二面角的大小为.A 1arccos 3 .B 1arccos 3π- .C 1arccos 23π- .D 1arccos 3-（四）走向高考：8.（07陕西）一个正三棱锥的四个顶点都在半径为1的球面上，其中底面的三个顶点在该球的一个大圆上，则该正三棱锥的体积是 .A 433 .B 33 .C 43 .D 1239.（07辽宁）若一个底面边长为2，的正六棱柱的所有顶点都在一个平面上，则此球的体积为10.（07全国Ⅱ）一个正四棱柱的各个顶点在一个直径为2cm 的球面上。
2023考研高昆仑数学零基础高数下导学讲前言高数是考研数学的重要组成部分，对于零基础的考生而言，掌握高数的基本知识是非常重要的。
本文将以2023考研高昆仑数学零基础高数下导学讲为主题，为考生介绍高数的主要内容，并提供一些学习的建议和方法。
1. 函数与极限1.1 函数的概念函数是数学中非常重要的概念，它是一种对应关系，将一个自变量映射到一个因变量。
函数的定义域和值域是函数的重要属性，需要注意的是，函数并不一定能将所有的自变量映射到因变量上。
1.2 极限的概念极限是函数中非常重要的概念，它描述了函数在自变量趋近于某个值时的变化趋势。
极限的计算需要用到一些基本的极限定理和极限运算法则。
1.3 一元函数的极限对于一元函数，其极限可以用左极限和右极限表示。
一元函数的极限计算需要根据函数的特性和极限的定义进行具体分析。
1.4 函数的连续性连续性是函数性质的一个重要方面，一个函数在某个点连续表示在这个点处没有跳跃或断裂的情况发生。
函数的连续性可以通过函数在某个点处是否存在极限来判断。
2. 导数与微分2.1 导数的概念导数是函数在某个点处的变化率，可以理解为函数曲线在这一点处的切线斜率。
导数具有一些基本的运算法则，比如导数的线性性质和乘积法则等。
2.2 函数的求导法则函数求导是一种重要的计算技巧，通过应用导数的运算法则，可以求解各种复杂函数的导数。
常见的函数求导法则包括常数的导数、幂函数的导数、指数函数和对数函数的导数等。
2.3 高阶导数与隐函数求导除了一阶导数外，函数还可以有二阶导数、三阶导数等高阶导数。
对于隐函数，其导数的求解需要应用隐函数求导法则。
2.4 微分与微分中值定理微分是导数的微元，它表示函数在某点附近的变化情况。
微分中值定理是微分学中的一个重要定理，它揭示了函数在某个区间内一定存在的特殊点。
3. 积分与不定积分3.1 不定积分的概念不定积分是积分的一种形式，表示对函数求原函数。
不定积分的计算需要应用一些基本的积分法则和常见的不定积分公式。
考研数学满分高昆仑简介
高老师讲题讲的也很清楚，喜欢讲一些有代表性的经典题，对个人水平提高很有帮助。
不过高老师讲的题都很有代表性，很有深度，基础差的人听不懂，就抱怨高老师讲的不好。
老师讲的很适合中等及以上的学生。
他讲的题一般都有难度，不过讲的很详细，基础差不多，都能听懂，去年也押到了题，讲一些简单的题确实没意思，报班看视频就看一些看书就能懂的题，感觉还不如自己看，数学想考高分的，跟着高老师绝对没错，还有就是他跟张某是一个团队的。
高昆仑老师是我最喜欢的考研数学老师，高昆仑老师讲的很好，认真听你就知道了
高老师人很体贴，讲题讲的也很清楚，喜欢讲一些有代表性的经典题，对个人水平提高很有帮助。
不过高老师讲的题都很有代表性，很有深度，基础差的人听不懂，就抱怨高老师讲的不好。
老师讲的很适合中等及以上的学生。
张某和汤某等的课我也听过，张某感觉听着虽然有趣，但真正学的东西很少。
汤某讲的大部分题都比较基础，听着有点浪费时间，不适合拔高。
高昆仑的课真的全是干货，不吹嘘，没废话，讲的特别认真，整个节奏很适合自己，真的很棒的一个老师。
他讲的题一般都有难度，不过讲的很详细，基础差不多，都能听懂，去年也押到了题，讲一些简单的题确实没意思，报班看视频就看一些看书就能懂的题，感觉还不如自己看，数学想考高分的，跟着高
老师绝对没错，还有就是他跟张某是一个团队的。
课题：函数的值域与最值教学目标：理解函数值域的意义；掌握常见题型求值域的方法，了解函数值域的一些应用.教学重点：求函数的值域与最值的基本方法。
（一）主要知识：1.函数的值域的定义；2.确定函数的值域的原则：定义域优先原则3.求函数的值域的方法.（二）主要方法：求函数的值域的方法常用的有：直接法，分离常数法，换元法，配方法，判别式法，不等式法，利用某些函数的有界性法，数形结合法，函数的单调性法，利用导数法，利用平移等.（三）典例分析：问题1. 求下列函数的值域：2；~~2 ------- 3x 十11 y=3x -x 2;2 y-,-x -6x-5 ;3 y二x -24 y = 2x —3 、4x —13 ;5 y = 2x" log3、一x —1 x ：= 2, 101;6 y =x .口 ;7 y=|x-1| |x 4|;8 y J；；1+32 2s 、2x —x+2 2x —x+1, 1、“八1 -sinx9 y 2; 10 y (x ); 11y =x2x 12x —1 2 2 — cosx12 y x2 4 、x2 2x 10 ;问题2. 1求函数y =log1 x2 -4x • 5的值域；222 已知f (x) =2 log3 x , x • 1,3 1,求函数y 二I f (x) 1 ■ f x2的值域；3若函数f (x)的值域为8冷，求yjx)的值域.I、可题3 .已知函数y= —b的值域为1-1,4 ],求常数a、b的值x +1（四）巩固练习：2x1.函数y二一的值域为2x+12.若函数f （x） =log a X在［2, 4］上的最大值与最小值之差为2，则a =3.已知f（x） =2x3-6x1 2• a（a是常数），在〔-2,2 1上有最大值3，那么在1-2,2 1上的最小值是 A -5 B. -11 C. -29 D. -37（五）课后作业：1.求下列函数的值域： 1 y h€x，2-J-x （x：= 10,11）；2 y = • 5 - x + log* x ；3 y= ,x-x x_0 ；3x 5,^05 y = x 5,0 ：： x 虫1-2x 8,x 112.函数y x 的值域是3 -1A ：；：—=, -1 B. (v,0)U(0, ：：) C. T, D. (Y；_1)U(0,=)23•已知函数f(x) =x 4x，贝U f(2cos^ -1)的值域是_______________________4.函数f （x ） —2mx • 3在区间1.0,2 ］上的值域为1-2,31，则m 的值为（）A. 一.,5或 5B. .5或 4C. 、、5D •专5. （ 07江苏通州一中质检）函数 y - x -、、x • 2的最小值为 ____________________6.（ 07江苏）已知函数f （x ） =x 3 -12x 8在区间1-3,31上的最大值与最小值分别为 M 、m ，则 M —m = _____ .7.若函数f （x ） =lx 3 - x • a 的定义域和值域均为23x9.( 06长春四市一模)函数y 二二x <0的值域是x + x +1A. 1-3,0B. 1-3,1C.D. -：：,03 ——10.（06新海中学模拟）函数y的定义域是 」：，1 U 〔2,5，则其值域是x T1,b 丨b • 1，求a 、b 的值8.函数y 二A. 124x 8x 13 6(x 1)B .32x 抵-1的最小值是（ C. 2 D. 311.求函数y =2x 2 -3 4x -1Lx <0的值域12. 定义在R 上的函数y = f (x)的值域为La, b 1，则函数y = f (x • a)的值域为 A.l2a, a b I B. 0, b -a 1 C. la, bl D J -a, a b 113. 已知f(x 199^ 4x 2 4x 3(^ R)，那么函数f(x)的最小值为 ________________________________14. 若f (x)的值域为 0,2，则g(x) = f (x-2007)-1的值域为 A. -1,3 ] B. -1,1 ] C. -2008, -2006 ]D.以上都不对15. ( 07江西)设函数 y =4 • log 2(x-1)(x > 3)，则其反函数的定义域为 ____________1 116.已知函数 f (x)a 0,x 0 .a x1若f (x)在 m,n 】上的值域是〔m,n 】，求a 的取值范围，并求相应的m,n 的值;A -：：,0 u.1,2B. -:-,2 IC. \J\2,I 2丿1亠 i D. 0,：：2若f(x) w 2x在0, •：：上恒成立，求a的取值范围(六)走向高考：191.(06全国n)函数f(x)=£|x - n的最小值为n 二A. 190B. 171C. 90D. 452. ( 04湖北)函数 f (x)二a x log a(x 1)在［0,1］上的最大值与最小值之和为1C. 2D. 4则a的值为 A —43. ( 04湖北文)已知x 一5，贝y f(x) = x 5有2 2x —4（06上海文）若曲线 y =2" +1与直线y = b 没有公共点，贝U b 的取值范围为.8. （ 06福建文）已知f （x ）是二次函数，不等式 f （x ） <0的解集是 0,5 , 且f （x ）在区间1-1,4 1上的最大值是12. (I )求f(x)的解析式；4. 5. 6. 5 5A.最大值-B.最小值- 4 4C.最大值1D.最小值1（07重庆文）函数f （x ） —. x^2x 2 x4的最小值为（06安徽）设a 0，对于函数A 有最大值而无最小值 C.有最大值且有最小值sin x + af x（0 ：：： x ：：：二），下列结论正确的是sin xB.有最小值而无最大值 D.既无最大值又无最小值（06陕西文）函数f （x ）二1□A. 0,1B. 0,11-R 的值域是 C. 1-0,1D. 1-0,117.37(n)是否存在在自然数m，使得方程f(x) 0在区间(m,m 1)内有且只有两个不x等的实数根？若存在，求出所有m的值；若不存在，说明理由.。
课题：映射与函数教学目标：了解映射的概念，在此基础上加深对函数概念的理解；能根据函数的三要素判断两个函数是否为同一函数；理解分段函数的意义.教学重点：函数是一种特殊的映射，而映射是一种特殊的对应；函数的三要素中对应法则是核心，定义域是灵魂.（一）主要知识：1. 映射与函数的概念；2. 函数的三要素及表示法，两个函数相同的条件；3. 正确理解函数值的含义，掌握函数值的求法，会灵活解决有关函数值的问题；特别是涉及分段函数或复合函数的值的问题•（二）主要方法：1. 对映射有两个关键点：一是有象，二是象惟一，缺一不可；2. 对函数三要素及其之间的关系给以深刻理解，这是处理函数问题的关键；3. 理解函数和映射的关系，函数式和方程式的关系.（三）典例分析：问题1.已知集合P =^x Q<x<4｝ , Q=｛x0^x^2｝，下列不.表.示.从P到Q的映射是A. f : x > y =2xB. f : x》y=3xC. f : x—；y =£xD. f : x—y = x问题2. （05黄岗模拟）下列从M到N的各对应法则f i（i =1,2,3,4 ）中哪些是映射？哪些是函数？哪些不是映射？为什么？1 M -｛直线Ax By ^0｝, N 二R , f1：求直线Ax By C =0 的斜率；2 M =｛直线Ax By 0 ｝, N -0 —：：J , f2:求直线Ax By C = 0 的倾斜角；3当M=N=R , f3:求M中每个元素的正切；4 M二N = x 一0 ?, f4:求M中每个元素的算术平方根.5 M =｛平面〉内的矩形｝, N =｛平面〉内的圆｝, f s :作矩形的外接圆（此小题为编者自拟）问题3. 1已知x,y在映射f作用下的象是x y,xy .①求-2,3在f作用下的象②若在f作用下的象是2,3，求它的原象2设集合A和B都是实数集，映射f : A》B把集合A中的元素x映射到集合B中的元素x3 -x 1，则在映射f下，象1的原象组成的集合是A 4 BJ-1,0,V C.（0 D.「—2,—1,0l问题4. 下列各对函数中，相同的是丄2 / ------A. f(x) =x, g(x) =：〔x2B. f(x) =、1-x2, g(x)=1-x , x 1-1,11C. y = f(x), g(x) = f(x+1) , x^RD. f(x) = lg(打,g(x)=lg2，x问题5.①（05浙江文）设f （x） = x T - x ,则f -f （；）］=A. -2B. 0C. 4D. 1笑(05山东)函数sin（兀x2）, 一1 c x < 0, 卄一八一“小f（xH x；，若f 1 f a =2,$xJL,xZ0.则a的所有可能值为A. 1 B•血 C. 1 丘 D. 1 丘2 ，2 ，2问题 6.矩形ABCD的长AB =8，宽AD =5，动点E、F分别在BC、CD上，且CE二CF二x , 1将厶AEF的面积S表示为x的函数f(x)，求函数S=f(x)的解析式；2求S的最大值.(四)巩固练习:21. 1 A 二 R ， B ={ y | y 0}， f : x — y =|x| ；2 A ={x |x _2,x 二 N }， B -〔y | y _ 0,y 二 N ?, f : x —； y = x 2-2x 2 ；3 A = {x | x 0}， B = {y | y R}， f : x —； y 二 x .上述三个对应 ______________ 是A 到B 的映射.1 12. 给定映射f : (x, y)r (2x y,xy)，点(一，)的原象是 _______________ __ _____6 6 3.下列函数中，与函数 y 二x 相同的函数是2A y = — B. y=(、. x)2 C.y=lg10xD.y = 2xx-3,(^10)□上4.设函数f (x)，则f (5)=lf(f(x+5)),(x<10)5. ( 06湖北八校一联)设 f ,g 都是由表一映射f 的对应法则 则与f1相同的是 A 6. ( 06灌云模拟)设 M Ma,b,c?，从M 到N 的映射f 满足f (a) • f(b) 一 f(c),试确定这样的映射 f 的个数为A. 1B. 2C.3D.4(五) 课后作业：1.设A =「x|O 乞x 乞2},B =「y|1乞2二在下图中，能表示从集合 A 到集合B 的映射是原象 1 2 3 4 象4 3 2 1lOg2X原象1 2 3 4 象 3 4 2 1A 到A 的映射，其对应法则如下表(从上到下)表二 映射f 的对应法则B. g 〔f(2)lC. g 〔f(3)lD.g[f(4)] A.B .z z = (x, y ),x, y € R,x2+ y2—12y + 27 兰0〉到集合B = R 的映射2.已知从集合A =：2f : z > -，则该映射的象集为xA一：：，_-、3 U .3, ：： B. 卜-』3, -3 C. -.3, .3 D.以上都不对3. ( 04北京东城模拟)设映射 2—X - 2x是实数集M到实数集N的映射，若对于实数p • N，在M中不存在原象，则p的取值范围是A. 1, ：：B. 1, ：：C. 一：：,1D. -：：,114.设集合A」1,2,3，B-4,5,6?，定义映射 f : A > B，使对任意2 2X - f (x) X f (x)是奇数，则这样的映射f的个数为A. 7B. 9C. 10D. 1825.若g(x) =1 -2x, f (g(x))晋& = 0)，则f(A )A. 1B. 3C. 15D. 306•已知f(x) = P "王0)，则不等式x+(x + 2)f(x+2)兰5的解集是[-1 (xcO)2x +17.设A=R , B=R , f : x 是A—；B 的映射，21设a • A，则a在B中的象是什么？s在映射f的象是什么?2设r A，那么t 1在B中的象是什么？3设s，A，若s-1在映射f下的象为5，则s应是多少?(六)走向高考:1. ( 06陕西)为确保信息安全,信息需加密传输,发送方由明文T 密文(加密),接收方由密文 T 明文(解密),已知加密规则为：明文 a 、b 、c 、d 对应密文a 2b , 2b c , 2c 3d , 4d .例如：明文1,2,3,4对应密文5,7,18,16.当接收方收到密文14,9,23,28时，则解密得 到的明文为A. 4,6,1,7B. 7,6,1,4C. 6,4,1,7D. 1,6,5,72. ( 06浙江)函数f : “,2,3丨一；；1,2,3 [满足f(f(x)) = f(x)，则这样的函数个数共有A. 1个B. 4个C. 8个D.10个3. ( 06广东文)对于任意的两个实数对(a,b)和(c,d)，规定：(a,b)=(c,d),当且仅当 a 二c,b =d ；运算"：”为：(a,b) ： (Gd) =(ac 「bd,bc ad)； 运算“二”为：(a,b)二(c,d) =(a c,b d)，设 p,q R ，若(1,2)： (p,q)=(5,0),则(1,2)二(p,q)=A. (4,0)B. (2,0)C. (0,2)D. (0,-4)4. ( 03全国)已知f 5『(x ) =lgx ，则f(2)二( )A. lg2B. lg 32C. lg丄1 D.-lg23252e x",x ：25. ( 06山东文)设1 f (X ) 2,则 f (f (2))的值为[log 3 (x -1 ,x_2A. 0B. 1C. 2D. 36. ( 07北京)已知函数f (x) , g(x)分别由下表给出:则f[g(1)]的值为___________ ；满足f[g(x)] g[f(x)]的x 的值是 ______________。
课题：函数的图像考纲要求：1.熟练掌握基本函数的图象；2.能正确地从函数的图象特征去讨论函数的主要性质；3.能够正确运用数形结合的思想方法解题． 教材复习一、作图方法：描点法和利用基本函数图象变换作图；1.描点法作图：方法步骤：(1)确定函数的定义域；(2)化简函数的解析式；(3)讨论函数的性质即奇偶性、周期性、单调性、最值(甚至变化趋势)；(4)描点连线，画出函数的图象．2.图象变换作图： ①平移变换：（1）水平平移：函数()y f x a =+的图像可以把函数()y f x =的图像沿x 轴方向向左(0)a >或向右(0)a <平移||a 个单位即可得到；（2）竖直平移：函数()y f x a =+的图像可以把函数()y f x =的图像沿x 轴方向向上(0)a >或向下(0)a <平移||a 个单位即可得到. ②对称变换：（1）函数()y f x =-的图像与函数()y f x =的图像关于y 轴对称； （2）函数()y f x =-的图像与函数()y f x =的图像关于x 轴对称； （3）函数()y f x =--的图像与函数()y f x =的图像关于原点对称；（4）函数1()y f x -=的图像与函数()y f x =的图像关于直线y x =对称； （5）函数()y f x =的图像与函数)2(x a f y -=的图像关于直线a x =称. ③翻折变换：（1）函数()y f x =的图像可以将函数()y f x =的图像的x 轴下方部分沿x 轴翻折到x 轴上方，去掉原x 轴下方部分，并保留()y f x =的x 轴上方部分即可得到； （2）函数()y f x =的图像可以将函数()y f x =的图像右边沿y 轴翻折到y 轴左边替代原y 轴左边部分并保留()y f x =在y 轴右边部分即可得到． ④伸缩变换：（1）函数()y af x =(0)a >的图像可以将函数()y f x =的图像中的每一点横坐标不变纵坐标伸长(1)a >或压缩（01a <<）为原来的a 倍得到；（2）函数()y f ax =(0)a >的图像可以将函数()y f x =的图像中的每一点纵坐标不变横坐标伸长(1)a >或压缩（01a <<）为原来的1a 倍得到.二、具有对称性的抽象函数：①函数()f x 对于定义域内的任意x ，都有()()f a x f b x +=-，则()f x 是关于直线2a b x +=对称的函数；②函数()f x 对于定义域内的任意x ，都有()()f a x f b x +=--，则()f x 是关于直线2,0a b +⎛⎫⎪⎝⎭对称的函数；③()f x 关于点(),a b 对称⇔()2f x b =-(2)f a x -.基本知识方法：1.获得函数图像的两种途径：描点法和利用基本函数图象变换作图；2.三种图象变换：平移变换、对称变换和伸缩变换；3.识图：分布范围、变化趋势、对称性、周期性等等方面．4.函数图像选择题快速解题的六个依据：①定义域；②值域；③奇偶性(更广即对称性）；④单调性；⑤特殊值；⑥最值(甚至变化趋势，渐近线等).典例分析： 考向一：作图问题1．分别画出下列函数的图象：()1321x y x +=-； ()212xy ⎛⎫= ⎪⎝⎭；()3221y x x =--；()4)(log 21x y -=； ()5lg y x =； ()6lg 1y x =+.考向二 知图选式与知式选图问题2：()1函数()y f x =与()y g x =的 图像分别如图①②所示：则函数()()y f x g x =⋅的图像可能是()2（07福建文）图中的图象所表示的函数的解析式为.A 312y x =- (02)x ≤≤.B 33122y x =-- (02)x ≤≤ .C 312y x =-- (02)x ≤≤ .D 11y x =--(02)x ≤≤()3（2013四川）函数231x x y =-的图象大致是考向三 有关对称问题问题3：()1设()f x 是(),-∞+∞上的奇函数，对任意实数x ，都有(2)()f x f x +=-，当11x -≤≤时，3()f x x =；①求证：直线1x =是函数()f x 图像的一条对称轴； ②当[1,5]x ∈时，求函数()f x 的解析式()2（06全国Ⅱ）函数()y f x =的图像与函数2()log (0)g x x x =>的图像关于原点对称，则()f x 的表达式为 .A 21()(0)log f x x x=> .B 21()(0)log ()f x x x =<- .C 2()log (0)f x x x =-> .D 2()log ()(0)f x x x =--<()3（2013新课标Ⅰ）若函数()()22()1f x x x ax b =-++的图像关于直线2x =-对称，.A.B.C.D则()f x 的最大值是考向四 函数图象的应用问题4：()1(2010湖北)若直线y x b =+与曲线3y =b 的取值范围是： .A 1,1⎡-+⎣ .B 1⎡-+⎣ .C 1⎡⎤-⎣⎦.D 1⎡⎤-⎣⎦()2（03全国）使()2log 1x x -<+成立的x 的取值范围是课后作业：1.函数25++=x x y 图象关于点P 中心对称，则点P 坐标是.A ()2,1-- .B ()2,1- .C ()2,1- .D ()2,12.如图，定义在[)1,-+∞上的函数的图像由一条线段和抛物线的一部分组成，则()f x 的解析式是3.若直线y x b =+与函数21y x =-的图象有两个不同的交点，则b 的范围是4.已知函数2()2f x x x =-，方程()f x a =有6个不同的实根，则实数a 的取值范围是 .A 1a <- .B 10a -<< .C 01a << .D 1a >5.（2013衡水中学第三次调研）函数()log 1a y x =+()1a >的图像大致是6.已知函数2()4f x x =-，()g x 是定义在()(),00,-∞+∞U 上的奇函数，当0x >时，2()log g x x =，则函数()()y f x g x =的大致图象为.A .B .C .D.A .B .C .D7.函数()f x 的部分图像如图所示，则函数()f x 的解析式是 .A ()sin f x x x =+ .B cos ()xf x x=.C ()cos f x x x = .D ()()()23f x x x x ππ=--走向高考：1.（08全国）函数1()f x x x=-的图像关于 .A y 轴对称.B 直线x y -=对称 .C 坐标原点对称 .D 直线x y =对称2（05北京春） 函数x x f 2log )(=的图象是3.（05北京文）为了得到函数321x y -=-的图象，只需把函数2x y =上所有点.A 向右平移3个单位长度，再向下平移1个单位长度.B 向左平移3个单位长度，再向下平移1个单位长度 .C 向右平移3个单位长度，再向上平移1个单位长度 .D 向左平移3个单位长度，再向上平移1个单位长度4.（2013北京）函数()f x 的图象向右平移1个单位长度,所得图象与x y e =关于y 轴对称,则()f x = A.1x e + B. 1x e - C. 1x e -+ D. 1x e --5.（04全国Ⅱ文）函数x y e =-的图象.A 与x y e =的图象关于y 轴对称； .B 与x y e =的图象关于坐标原点对称；.C 与x y e -=的图象关于y 轴对称；.D 与x y e -=的图象关于坐标原点对称.6.（高考）如果函数sin 2cos 2y x a x =+的图像关于8x π=-对称，那么a =.A .B .C 1 .D 1-7.（02上海）函数],[|,|sin ππ-∈+=x x x y 的大致图象是y yπ π π- O π x -π Oπ xπ- （A ）y y ππ π- O π x -π O π xπ- -π （C ）8.（07四川）函数x x g x x f -=+=122)(log 1)(与在同一直角坐标系下的图象大致是.A .B .C .D 9.（2013山东）函数cos sin y x x x =+的图象大致是10.（09山东）函数x xx x e e y e e--+=-的图像大致为11.（06上海文）若曲线21x y =+与直线y b =没有公共点，则b 的取值范围是12.（2011海南）已知函数()y f x =的周期为2,当[1,1]x ∈-时2()f x x =,那么函数()y f x =的图象与函数lg y x =的图象的交点共有 .A 10个 .B 9个 .C 8个 .D 1个。
课题：数学归纳法考纲要求：1.了解数学归纳法的原理.2.能用数学归纳法证明一些简单的数学命题. 教材复习1.数学归纳法是证明一个与正整数n 有关的命题，可按下列步骤进行：()1（归纳奠基）证明当n 取 时命题成立；()2(归纳递推)假设当n k =(*k N ∈，k ≥0n )时命题成立，证明当 时命题也正确. 2.应用数学归纳法时要特别注意：()1数学归纳法证明的对象是与 有关的命题；()2用数学归纳法证题时，两个基本步骤缺一不可递推基础不可少，归纳假设要用到，结论写明莫忘掉.3.证题时要注意两凑：一凑归纳假设，二凑目标.典例分析：考点一 用数学归纳法证明数学命题时原理及两个步骤的考查问题1．()1用数学归纳法证明3n≥3(,n n N n ∈≥3）时，第一步应验证 .A 1n = .B 2n = .C 3n = .D 4n =()2用数学归纳法证明2122+++…12221n n +++=-()n N +∈的过程中，在验证1n =时，左端计算所得的项为 .A 1 .B 12+ .C 2122++ .D 231222+++()3（2012渭南中学月考）用数学归纳法证明不等式11124+++ (11127264)n -+>成立， 起始值至少应取为 .A 7 .B 8 .C 9 .D 10()4用数学归纳法证明“11123+++ (1)21n n +<-（1n >）”，由()1n k k =>不等式成立，推证1n k =+时，左边应增加的项的项数是考点二 用数学归纳法证明整除性问题问题2．求证：49161n n +-能被64整除（*n N ∈）.考点三 用数学归纳法证明恒等式问题3．n N +∈，求证：1111234-+-+…111121212n n n n +-=++-++…12n +.考点四 用数学归纳法证明不等式问题4．求证：11111223422n n --+++⋅⋅⋅+>（n ≥2，n N ∈）考点五 用数学归纳法证明几何问题问题5．求证：凸n 边形的对角线条数为()1()32f n n n =-（n N ∈，n ≥3).考点六 归纳—猜想—证明模式的考查 问题6．在各项为正的数列{}n a 中，数列的前n 项和112n n n S a a ⎛⎫=+ ⎪⎝⎭. ()1求1a ，2a ，3a ；()2由()1猜想数列{}n a 的通项公式，并且用数学归纳法证明你的猜想.课后作业：1.观察下列式子： ,474131211,3531211,23211222222<+++<++<+，则可以猜想的结论为：2.用数学归纳法证明“()()()()1221321n n n n n n ++⋅⋅⋅+=⋅⋅⋅⋅⋅-”，从“k 到1k +”左端需增乘的代数式为.A 21k + .B ()221k + .C 112++k k .D 132++k k3.（07重庆市重点中学二联）如图，第n 个图形是由正2n +边形“扩展”而来（1n =，2，3，…），则第2n -个图形中共有 个顶点.4.凸n 边形有()f n 条对角线，则凸1n +边形有对角线条数(1)f n +为.A ()1f n n ++ .B ()f n n + .C ()1f n n +- .D ()2f n n +-5.平面内有n 条直线，其中任何两条不平行，任何三条不共点，求证：这n 条直线把平面分成()21()22f n n n =++个区域.6.用数学归纳法证明：222111123n++⋅⋅⋅+<（其中n ≥2，且*n N ∈）.7.(2013北京海淀模拟)数列{}n a 满足2n n S n a =-()n N +∈. ()1计算1234,,,a a a a ，并由此猜想通项公式n a ；()2用数学归纳法证明()1中的猜想.走向高考： 8.（07上海）设)(x f 是定义在正整数集上的函数，且)(x f 满足：“当2()f k k ≥成立时，总可推出(1)f k +≥2)1(+k 成立”．那么，下列命题总成立的是 .A 若(3)9f ≥成立，则当1k ≥时，均有2()f k k ≥成立 .B 若(5)25f ≥成立，则当5k ≤时，均有2()f k k ≥成立 .C 若49)7(<f 成立，则当8k ≥时，均有2)(k k f <成立 .D 若25)4(=f 成立，则当4k ≥时，均有2()f k k ≥成立9. (06湖南）已知函数()sin f x x x =-,数列{n a }满足: 101a <<，1()n n a f a +=，1,2,3,n =求证:()1 101n n a a +<<<;()23116n n a a +<.10.(2009陕西) 已知数列{}n x 满足， *1111,21n nx x n N x ∈+＋’＝＝. ()I 猜想数列{}n x 的单调性，并证明你的结论；(Ⅱ)证明：1112|()65n n n x x -+-|≤.。
