利用状态观测器实现状态反馈的系统设计

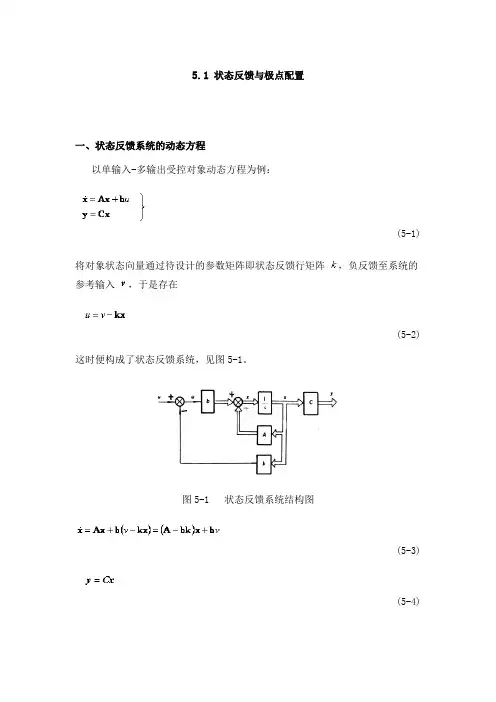
5.1状态反馈与极点配置一、状态反馈系统的动态方程以单输入-多输出受控对象动态方程为例：(5-1)将对象状态向量通过待设计的参数矩阵即状态反馈行矩阵，负反馈至系统的参考输入，于是存在(5-2)这时便构成了状态反馈系统，见图5-1。

图5-1 状态反馈系统结构图(5-3)(5-4)式中v为纯量，为维向量，为维矩阵，为维向量，为维行矩阵，为维向量，为维矩阵。

为闭环状态阵，为闭环特征多项式。

二、用状态反馈使闭环极点配置在任意位置上的充要条件是：受控对象能控证明若式(5-1)所示对象可控，定可通过变换化为能控标准形，有若在变换后的状态空间内引维状态反馈矩阵：(5-5)其中分别为由状态变量引出的反馈系数，则变换后的状态反馈系统动态方程为：(5-6)(5-7)式中(5-8)该式与仍为能控标准形，故引入状态反馈后，系统能控性不变。

特征方程为：(5-9)显见，任意选择阵的个元素，可使特征方程的个系数满足规定要求，能保证特征值（即闭环极点）任意配置。

将逆变换代入式(5-6)，可求出原状态空间内的状态反馈系统状态方程：(5-10)与式(5-3)相比，式(5-10)所示对象应引入状态反馈阵为：(5-11)需指出，当受控对象可控时，若不具有能控标准形形式，并不必象如上证明那样去化为能控标准形，只要直接计算状态反馈系统闭环特征多项式，这时，其系数为的函数，与给定极点的特征多项式系数相比较，便可确定。

能控的多输入-多输出系统，经如上类似分析可知，实现闭环极点任意配置的状态反馈阵K为维。

若受控对象不稳定，只要有能控性，完全可由状态反馈配置极点使系统稳定。

状态变量受控情况下，引入状态反馈表示增加一条反馈通路，它能改变反馈所包围环节的传递特性，即通过改变局部回路的极点来改变闭环极点配置。

不能控状态变量与控制量无关，即使引入状态反馈，对闭环极点位置也不会产生任何影响，这是因为传递函数只与系统能控、能观测部分有关的缘故。

若不能控状态变量是稳定的状态变量，那么系统还是能稳定的，否则，系统不稳定。

现代控制实验状态反馈器和状态观测器的设计现代控制实验中，状态反馈器和状态观测器是设计系统的重要组成部分。

状态反馈器通过测量系统的状态变量，并利用反馈回路将状态变量与控制输入进行耦合，以优化系统的性能指标。

状态观测器则根据系统的输出信息，估计系统的状态变量，以便实时监测系统状态。

本文将分别介绍状态反馈器和状态观测器的设计原理和方法。

一、状态反馈器的设计：状态反馈器的设计目标是通过调整反馈增益矩阵，使得系统的状态变量在给定的性能要求下，达到所需的一组期望值。

其设计步骤如下：1.系统建模：通过对被控对象进行数学建模，得到描述系统动态行为的状态空间表达式。

通常表示为：ẋ=Ax+Buy=Cx+Du其中，x为系统状态向量，u为控制输入向量，y为系统输出向量，A、B、C、D为系统的状态矩阵。

2.控制器设计：根据系统的动态性能要求，选择一个适当的闭环极点位置，并计算出一个合适的增益矩阵。

常用的设计方法有极点配置法、最优控制法等。

3.状态反馈器设计：根据控制器设计得到的增益矩阵，利用反馈回路将状态变量与控制输入进行耦合。

状态反馈器的输出为：u=-Kx其中，K为状态反馈增益矩阵。

4.性能评估与调整：通过仿真或实验，评估系统的性能表现，并根据需要对状态反馈器的增益矩阵进行调整。

二、状态观测器的设计：状态观测器的设计目标是根据系统的输出信息，通过一个状态估计器，实时估计系统的状态变量。

其设计步骤如下：1.系统建模：同样地，对被控对象进行数学建模，得到描述系统动态行为的状态空间表达式。

2.观测器设计：根据系统的动态性能要求，选择一个合适的观测器极点位置，以及一个合适的观测器增益矩阵。

常用的设计方法有极点配置法、最优观测器法等。

3.状态估计：根据观测器设计得到的增益矩阵，通过观测器估计系统的状态变量。

状态观测器的输出为：x^=L(y-Cx^)其中，L为观测器增益矩阵，x^为状态估计向量。

4.性能评估与调整：通过仿真或实验，评估系统的状态估计精度，并根据需要对观测器的增益矩阵进行调整。

现代控制实验--状态反馈器和状态观测器的设计-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN状态反馈器和状态观测器的设计一、实验设备PC 计算机，MATLAB 软件，控制理论实验台，示波器二、实验目的（1）学习闭环系统极点配置定理及算法，学习全维状态观测器设计法；（2）掌握用极点配置的方法（3）掌握状态观测器设计方法（4）学会使用MATLAB工具进行初步的控制系统设计三、实验原理及相关知识（1）设系统的模型如式所示若系统可控，则必可用状态反馈的方法进行极点配置来改变系统性能。

引入状态反馈后系统模型如下式所示：（2）所给系统可观，则系统存在状态观测器四、实验内容（1）某系统状态方程如下10100134326x x u •⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥----⎣⎦⎣⎦[]100y x =理想闭环系统的极点为[]123---.（1）采用 Ackermann 公式计算法进行闭环系统极点配置；代码：A=[0 1 0;0 0 1;-4 -3 -2];B=[1; 3; -6];P=[-1 -2 -3];K=acker(A,B,P)Ac=A-B*Keig(Ac)（2）采用调用 place 函数法进行闭环系统极点配置；代码：A=[0 1 0;0 0 1;-4 -3 -2];B=[1;3;-6];eig(A)'P=[-1 -2 -3];K=place(A,B,P)eig(A-B*K)'（3）设计全维状态观测器，要求状态观测器的极点为[]---123代码：a=[0 1 0;0 0 1;-4 -3 -2];b=[1;3;-6];c=[1 0 0];p=[-1 -2 -3];a1=a';b1=c';c1=b';K=acker(a1,b1,p);h=(K)'ahc=a-h*c（2）已知系统状态方程为：10100134326x x u •⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥----⎣⎦⎣⎦[]100y x =（1）求状态反馈增益阵K ，使反馈后闭环特征值为[-1 -2 -3]；代码：A=[0 1 0;0 0 1;4 -3 -2];b=[1;3;-6];p=[-1 -2 -3];k=acker(A,b,p)A-b*keig(A-b*k)（2）检验引入状态反馈后的特征值与希望极点是否一致。

状态反馈观测设计状态反馈观测器是一种用于估计系统状态的控制器组件。

它通过测量系统的输出和输入，并使用状态方程对系统状态进行估计。

以下是一个详细精确的状态反馈观测器设计步骤：1. 确定系统的状态方程：首先，需要确定系统的状态方程，通常采用线性时不变系统表示。

状态方程可以表示为：x' = Ax + Buy = Cx + Du其中，x是系统的状态向量，u是系统的输入向量，y是系统的输出向量，A、B、C和D是系统的系数矩阵。

2. 设计状态反馈控制器：使用控制理论中的状态反馈控制器设计方法，根据系统的要求和性能指标，选择合适的状态反馈增益矩阵K。

状态反馈控制器的输出可以表示为：u = -Kx3. 设计状态观测器：状态观测器的目标是估计系统的状态向量x。

根据系统的输出和输入，可以使用以下观测器方程进行状态估计：x̂' = A x̂ + Bu + L(y - C x̂)其中，x̂是状态观测器的估计状态向量，L是观测器增益矩阵。

4. 确定观测器增益矩阵L：观测器增益矩阵L的选择可以使用线性二次调节器（LQR）设计方法，根据系统的要求和性能指标，通过求解代数矩阵方程来确定L。

5. 实施状态反馈观测器：将状态反馈控制器和状态观测器结合在一起，形成一个状态反馈观测器控制系统。

系统的输入通过状态反馈控制器计算得到，系统的输出通过状态观测器估计得到，从而实现对系统状态的估计和控制。

6. 优化观测器性能：根据实际应用需求，可以通过调整观测器增益矩阵L来优化观测器的性能，例如减小状态估计误差、提高状态估计的收敛速度等。

以上是一个详细精确的状态反馈观测器设计过程。

根据具体的系统和应用需求，可能需要进行一些额外的步骤或调整来优化控制系统的性能。

基于时域观测器的系统状态估计与反馈控制设计概述：本文将讨论基于时域观测器的系统状态估计与反馈控制设计。

我们将详细介绍时域观测器的原理和设计方法，并探讨其在系统状态估计和反馈控制中起到的作用。

同时，我们还将讨论如何利用时域观测器来实现系统状态估计和反馈控制，并基于实例进行说明。

1. 时域观测器的原理时域观测器是一种用于估计系统状态的技术。

它通过测量系统的输出和输入信号，利用系统的数学模型对状态进行估计。

时域观测器的原理基于系统的状态方程和输出方程，通过对观测误差进行修正来实现状态估计。

2. 时域观测器的设计方法时域观测器的设计方法主要包括两个步骤：观测器增益的选择和观测器误差的修正。

观测器增益的选择可以通过最优化方法来实现，例如线性二次调节（LQR）方法。

观测器误差的修正可以通过状态误差修正器进行实现，例如卡尔曼滤波器。

3. 系统状态估计与时域观测器系统状态估计是指在没有直接测量系统状态的情况下，通过观测系统的输出和输入信号来估计系统的状态。

时域观测器可以作为一种常用的状态估计方法。

它利用系统的模型以及观测误差的修正来实现状态估计，并具有较好的性能和稳定性。

4. 反馈控制与时域观测器反馈控制是指通过对系统状态的测量和估计，根据某种控制策略对系统的输出进行调节和控制。

时域观测器能够提供对系统状态的估计，从而在反馈控制中发挥关键作用。

通过利用时域观测器估计的状态信息，我们可以设计合适的反馈控制器，实现对系统的稳定性、精度和鲁棒性的提高。

5. 实例分析：基于时域观测器的控制系统为了更好地理解基于时域观测器的系统状态估计和反馈控制设计，我们以一个控制系统为例进行分析。

假设我们要设计一个机器人的控制系统，根据外部环境的变化和用户的指令，控制机器人的运动。

首先，我们需要建立机器人的数学模型，包括系统的状态方程和输出方程。

然后，通过选择合适的观测器增益，并利用状态误差修正器对观测误差进行修正，实现对机器人状态的估计。

状态反馈观测设计-回复“状态反馈观测设计”是一种控制系统设计方法，通过观测被控对象的状态信息并将其反馈给控制器，从而实现对系统状态的精确控制。

在本文中，我们将分步介绍状态反馈观测设计的概念、原理、应用和设计步骤。

第一步：概念介绍状态反馈观测设计是一种基于状态反馈的控制方法。

在常规的控制系统设计中，通常只能通过对输出信号进行测量和反馈控制，而无法直接测量系统的内部状态。

然而，很多情况下，只通过输出控制往往无法满足控制要求，因为输出变量与系统内部状态之间存在时滞或非线性关系。

状态反馈观测设计通过引入状态估计器，估计系统的内部状态，并将此信息反馈给控制器，从而实现对系统状态的精确控制。

第二步：原理说明状态反馈观测设计的原理是基于状态观测器和状态反馈器。

状态观测器是一个被动观测系统，通过测量系统的输出和控制输入，利用状态方程和观测方程来估计系统的内部状态。

通过与实际状态进行比较，状态观测器可以得出误差，并将该误差作为反馈信号传递给状态反馈器。

状态反馈器接收状态观测器的误差信号，并生成相应的控制输出信号，以实现对系统的状态控制。

第三步：应用示例状态反馈观测设计在工程控制系统中有着广泛的应用。

例如，考虑一个机械臂控制系统，通过精确的控制关节角度可以实现机械臂的精确定位和运动。

然而，由于关节之间的耦合作用和机械臂的结构特性，只通过控制关节角度往往无法实现理想的控制效果。

此时，可以利用状态反馈观测设计来估计机械臂的内部状态，包括位置、速度和加速度等，从而实现对机械臂运动的精确控制。

第四步：设计步骤进行状态反馈观测设计的步骤如下：1. 确定系统的动态模型：根据实际系统的特性和工作原理，建立系统的动态方程。

这通常可以通过物理模型、数学模型或实验测量得到。

2. 输入输出选择：确定希望通过状态反馈观测设计实现的系统状态和控制输出。

这可以是系统的位置、速度、温度等需要精确控制的变量。

3. 设计状态观测器：根据系统的动态方程和输出方程，设计一个状态观测器来估计系统的内部状态。

实验6_状态反馈与状态观测器自动控制原理实验报告自动控制原理实验报告院系名称：仪器科学与光电工程学院班级：141715班姓名：武洋学号：14171073实验六状态反馈与状态观测器一、实验目的1. 掌握用状态反馈进行极点配置的方法。

2. 了解带有状态观测器的状态反馈系统。

3. 理解系统极点、观测器极点与系统性能、状态估计误差之间的关系。

二、实验内容1. 系统G(s)=10.05s2+s+1如图2.6.1所示，要求设计状态反馈阵K，使动态性能指标满足超调量，峰值时间。

图2.6.1二阶系统结构图2．被控对象传递函数为写成状态方程形式为式中; ;为其配置系统极点为S1,2=-仪器科学与光电工程学院班级：141715班姓名：武洋学号：14171073实验六状态反馈与状态观测器一、实验目的1. 掌握用状态反馈进行极点配置的方法。

2. 了解带有状态观测器的状态反馈系统。

3. 理解系统极点、观测器极点与系统性能、状态估计误差之间的关系。

二、实验内容1. 系统G(s)=10.05s2+s+1如图2.6.1所示，要求设计状态反馈阵K，使动态性能指标满足超调量，峰值时间。

图2.6.1二阶系统结构图2．被控对象传递函数为写成状态方程形式为式中; ;为其配置系统极点为S1,2=：其中维状态反馈系数矩阵，由计算机算出。

维观测器的反馈矩阵，由计算机算出。

为使跟踪所乘的比例系数。

三、实验原理1. 闭环系统的动态性能与系统的特征根密切相关，在状态空间的分析中可利用状态反馈来配置系统的闭环极点。

这种校正手段能提供更多的校正信息，在形成最优控制率、抑制或消除扰动影响、实现系统解耦等方面获得广泛应用。

在改善与提高系统性能时不增加系统零、极点，所以不改变系统阶数，实现方便。

2. 已知线形定常系统的状态方程为为了实现状态反馈，需要状态变量的测量值，而在工程中，并不是状态变量都能测量到，而一般只有输出可测，因此希望利用系统的输入输出量构成对系统状态变量的估计。

现代控制理论状态反馈和状态观测器的设计实验报告本次实验是关于现代控制理论中状态反馈与状态观测器的设计与实现。

本次实验采用MATLAB进行模拟与仿真，并通过实验数据进行验证。

一、实验目的1、学习状态反馈控制的概念、设计方法及其在实际工程中的应用。

3、掌握MATLAB软件的使用方法。

二、实验原理1、状态反馈控制状态反馈控制是指将系统状态作为反馈控制的输出，通过对状态反馈控制器参数的设计，使系统的状态响应满足一定的性能指标。

状态反馈控制的设计步骤如下：(1) 确定系统的状态方程，即确定系统的状态矢量、状态方程矩阵和输出矩阵；(2) 设计状态反馈控制器的反馈矩阵，即确定反馈增益矩阵K；(3) 检验状态反馈控制器性能是否满足要求。

2、状态观测器(1) 确定系统的状态方程；(2) 设计观测器的状态估计矩阵和输出矩阵；(3) 检验观测器的状态估计精度是否符合标准。

三、实验内容将简谐信号加入单个质点振动系统，并对状态反馈控制器和状态观测器进行设计与实现。

具体实验步骤如下：1、建立系统状态方程：（1）根据系统的物理特性可得单自由度振动系统的运动方程为：m¨+kx=0（2）考虑到系统存在误差、干扰等因素，引入干扰项，得到系统状态方程：（3）得到系统状态方程为：（1）观察系统状态方程，可以发现系统状态量只存在于 m 行 m 到 m 行 n 之间，而控制量只存在于 m 行 1 到 m 行 n 之间，满足可控性条件。

（2）本次实验并未给出状态变量的全部信息，只给出了系统的一维输出，因此需要设计状态反馈器。

（3）我们采用极点配置法进行状态反馈器设计。

采用 MATLAB 工具箱函数，计算出极点：(4) 根据极点求解反馈矩阵，得到状态反馈增益矩阵K：（1）通过矩阵计算得到系统的可观性矩阵：（2）由若干个实测输出建立观测器，可将观测器矩阵与可观测性矩阵组合成 Hankel 矩阵，求解出状态观测器系数矩阵：（3）根据系统的状态方程和输出方程，设计观测方程和状态估计方程，如下：4、调试控制器和观测器（1）经过上述设计步骤，将反馈矩阵和观测矩阵带入 MATLAB 工具箱函数进行仿真。

状态反馈器与状态观测器得设计一、实验设备PC 计算机,MATLAB 软件,控制理论实验台,示波器二、实验目得（1）学习闭环系统极点配置定理及算法,学习全维状态观测器设计法;（2）掌握用极点配置得方法（3）掌握状态观测器设计方法（4）学会使用MATLAB工具进行初步得控制系统设计三、实验原理及相关知识(1)设系统得模型如式所示若系统可控,则必可用状态反馈得方法进行极点配置来改变系统性能。

引入状态反馈后系统模型如下式所示:(2)所给系统可观,则系统存在状态观测器四、实验内容(1)某系统状态方程如下理想闭环系统得极点为、(1)采用 Ackermann 公式计算法进行闭环系统极点配置; 代码:A=[0 1 0;0 0 1;4 3 2];B=[1; 3; 6];P=[1 2 3];K=acker(A,B,P)Ac=AB*Keig(Ac)(2)采用调用 place 函数法进行闭环系统极点配置; 代码:A=[0 1 0;0 0 1;4 3 2];B=[1;3;6];eig(A)'P=[1 2 3];K=place(A,B,P)eig(AB*K)'(3)设计全维状态观测器,要求状态观测器得极点为代码:a=[0 1 0;0 0 1;4 3 2];b=[1;3;6];c=[1 0 0];p=[1 2 3];a1=a';b1=c';c1=b';K=acker(a1,b1,p);h=(K)'ahc=ah*c(2)已知系统状态方程为:（1）求状态反馈增益阵K,使反馈后闭环特征值为[1 2 3]; 代码:A=[0 1 0;0 0 1;4 3 2];b=[1;3;6];p=[1 2 3];k=acker(A,b,p)Ab*keig(Ab*k)(2)检验引入状态反馈后得特征值与希望极点就是否一致。

（3）比较状态反馈前后得系统阶跃响应。

代码:A1=[0 1 0;0 0 1;4 3 2];B1=[1;3;6];C1=[1 0 0];D1=[0];G1=ss(A1,B1,C1,D1);[y1,t1,x1]=step(G1);P=[1 2 3];K=acker(A1,B1,P);abk=A1B1*K;A2=abk;B2=B1;C2=C1;D2=D1;G2=ss(A2,B2,C2,D2);[y2,t2,x2]=step(G2);hold onplot(t1,x1)plot(t2,x2)(4)设计全阶状态观测器,要求状态观测器得极点为[5 6 7]。

状态反馈与状态观测器实验状态反馈与状态观测器一、实验目的1．自学全系列状态意见反馈布局极点的方法。

2．自学降维状态观测器的设计方法。

3．学习带有状态观测器的状态反馈系统的设计方法。

二、实验仪器1．el-at-ii型自动控制系统实验箱一台2．计算机一台三、实验建议1．1）用全状态反馈配置极点的方法，按给定的性能指标进行综合设计。

2）检验极点布局理论的正确性。

2.设计一个带有状态观测器的状态反馈系统。

四、实验前分析排序和设计已知被控系统如图所示：u10.05s+1x210.1sx1y图5-1被控系统结构图1、设计一个全状态反馈系统，闭环系统性能要求为ξ=0.707，ts≤0.2s.设计k阵，并图画出来尖萼电路图挑选适当元件参数。

2、假设x２不能直接测量，设计一个降维状态观测器将x２进行估计得到估计值，然后用2形成全系列状态意见反馈，并使闭环系统ξ=0.707，ts≤0.2s，并图画出来尖萼电路图挑选x1和x独以适当元件参数。

100k50k1uf1ufda1100k25k2-out650k2-out63100k+3+x2100k2-out6x1ad131k100k0-6out+321k0+1k100k01k0图5-2状态反馈系统演示电路图图5-3带有状态观测器的状态反馈系统模拟电路图五、实验步骤1.连接被测量典型环节的模拟电路。

电路的输入u1接a/d、d/a卡的da1输出，电路的输入u2接a/d、d/a卡的ad1输出。

检查有误后拨打电源。

2.启动计算机，在桌面双击图标[自动控制实验系统]运转软件。

3.测试计算机与实验箱的通信是否正常,通信正常继续。

如通信不正常查找原因使通信正常后才可以继续进行实验。

4.在实验课题下拉菜单中挑选实验二[二阶系统阶跃积极响应],具有状态观测器的状态反馈系统挑选实验五[状态意见反馈与状态观测器]，鼠标单击该选项弹头出来实验课题参数窗口。

5.观测表明的波形记录最小市场汇率量mp和调节时间ts的数值和积极响应动态曲线，并与理论值比较。